一种海洋重力扰动矢量水平分量的计算方法

蔡体菁,王 薇

(东南大学 仪器科学与工程学院,江苏 南京 210096)

0 引言

在捷联式重力矢量测量中,重力扰动矢量由重力仪中3个相互正交的加速度计输出所得,其输出包括重力矢量、载体运动加速度和加速度计偏差。在捷联惯导系统/全球导航卫星系统(SINS/GNSS)组合系统的卡尔曼滤波中,加速度计偏差和姿态误差在估计过程中是耦合的,不易区分[1]。在重力矢量测量中,分离重力扰动矢量水平分量和误差需额外测量或引入额外假设[2-4]。因此,本文提出了一种重力扰动矢量水平分量估计的两步法,将重力扰动矢量水平分量估计与惯导误差估计解耦。扩展卡尔曼滤波算法用于加速度计偏差和姿态误差角的估计和补偿,以得到计算地理坐标系下的比力。再利用精确估计的加速度计偏差和姿态角误差,建立重力扰动矢量水平分量的计算方程,从而得到当地地理坐标系下的比力。在此基础上,将重力扰动矢量水平分量用二阶马尔可夫随机过程描述,将其与加速度计的偏差分离,利用正向-平滑卡尔曼滤波估算地理坐标系与真实的当地地理坐标系间的误差角,从而准确估计重力扰动矢量水平分量。

1 比力计算

为了获得当地地理坐标系下的重力扰动矢量,需要精确的东向、北向和天向比力,以及精确的姿态误差角。从GNSS基站和移动站传递来的原始数据经过差分计算后,可得到速度和位置信息。因此,基于SINS/GNSS组合系统的状态和量测方程,SINS的加速度计偏差和姿态误差角可通过高精度捷联惯导算法和闭环扩展卡尔曼滤波精确确定,且在误差补偿后,可得到东、北、天向的比力。

以惯导误差和重力矢量仪器件误差为状态量,建立SINS/GNSS组合系统的状态方程,状态向量为

X=[φE,φN,φU,δvE,δvN,δvU,δL,δλ,δh,

(1)

SINS/GNSS组合系统的量测向量为

(2)

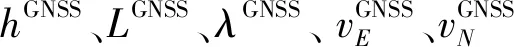
2 重力扰动矢量水平分量的计算方程

由于陀螺仪精度的影响,根据SINS/GNSS组合系统计算得到的比力是相对于计算地理坐标系的,该坐标系和真实地理坐标系间存在很小的角度误差,因此,重力扰动矢量的水平分量不能由比力计算的结果直接获得。进一步补偿姿态误差,可获得高精度的重力扰动矢量的水平分量。

由于加速度计偏差和重力扰动矢量水平分量难以区分,重力扰动矢量水平分量无法在卡尔曼滤波器中估计,为此建立重力扰动矢量水平分量的随机模型,从而将重力扰动矢量水平分量与加速度计偏差区分,在误差方程中估计重力扰动矢量水平分量。

引入计算地理坐标系和真实地理坐标系之间的姿态误差角φn=[φEφNφU]T,这两个坐标系下比力的关系为

(3)

根据姿态误差微分方程,SINS的姿态误差角方程为

(4)

式中:ωE,ωN,ωU为当地地理坐标系相对于惯性坐标系的旋转角速度在其坐标轴上的投影;εE,εN,εU为重力矢量仪在当地地理坐标系下的等效陀螺漂移。

在当地地理坐标系下,重力扰动矢量的水平分量的计算方程[5-6]为

(5)

重力扰动矢量的水平分量通过一个二阶高斯-马尔可夫随机过程表示,其状态方程为

(6)

式中:β为重力相关参数;pE,pN为中间变量;qE,qN分别为当地地理坐标系的东向和北向的重力扰动矢量噪声。

根据方程(1)-(6)可推得重力扰动矢量的状态方程组,并且状态向量为

X=[φE,φN,φU,δvE,δvN,ΔgE,pE,

ΔgN,pN]T

(7)

利用正向-平滑卡尔曼滤波器计算重力扰动矢量水平分量,首先使用正向卡尔曼算法进行预测和估计,再使用Rauch-Tung-Striebel (RTS)固定区间平滑算法进行反向平滑,RTS固定区间平滑算法的步骤为

(8)

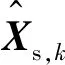
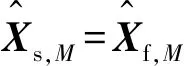
3 实验结果

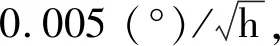
对此次船载海洋重力测量数据进行了海洋重力扰动水平分量计算,截取东西方向和南北方向的重复测线各两条,两组重复测线的轨迹如图1、2所示。舰船航行的平行速度为3 m/s,重力矢量仪的输出频率为200 Hz,GNSS的输出频率为2 Hz,采用差分GNSS获得位置和速度信息。

图1 东西向测线轨迹

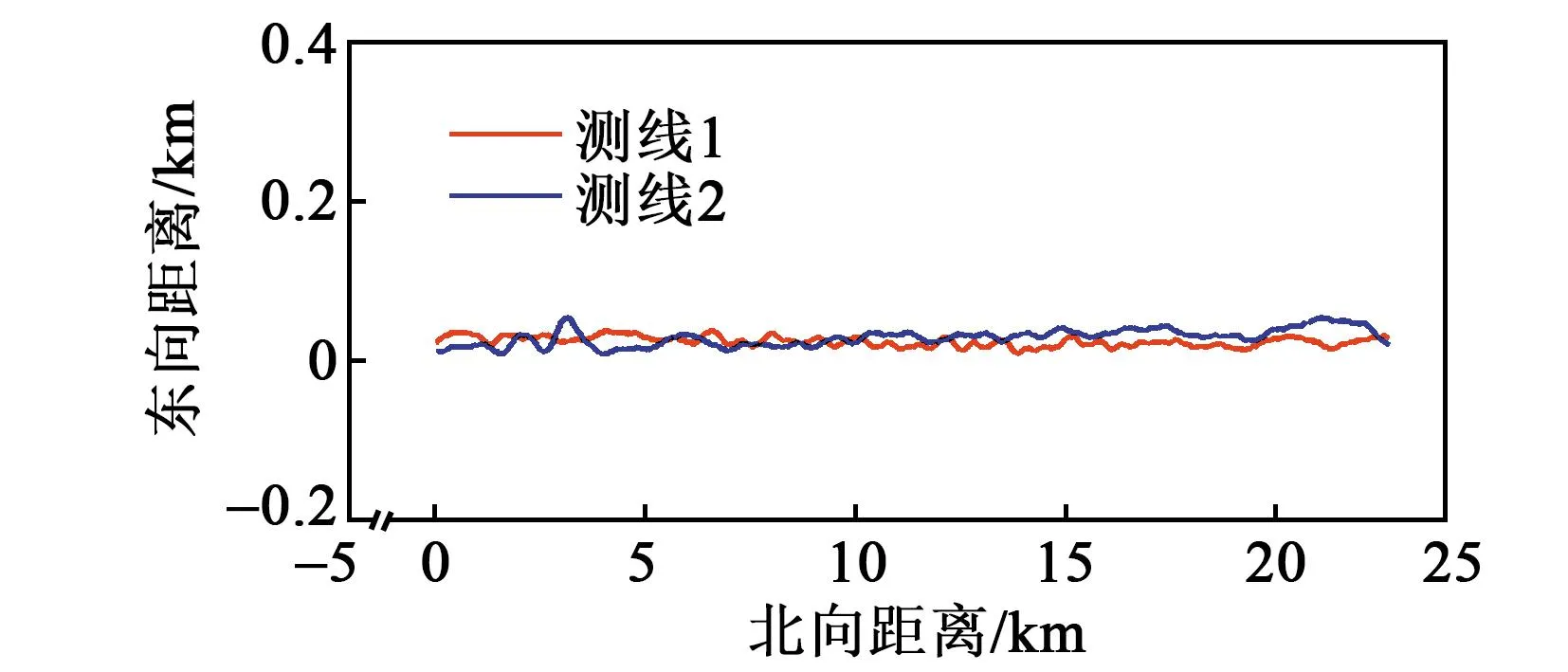
图2 南北向测线轨迹

两条东西向测线的重力扰动矢量水平分量计算结果如图3、4所示。由图可知,舰船在东西方向航行时,两条测线的东向、北向重力扰动重合情况较好,两条测线上的重力扰动水平分量存在的偏差在允许范围内,因此认为水平重力扰动能够从速度误差中分离出来。

图3 两条东西向测线重力扰动矢量东向分量

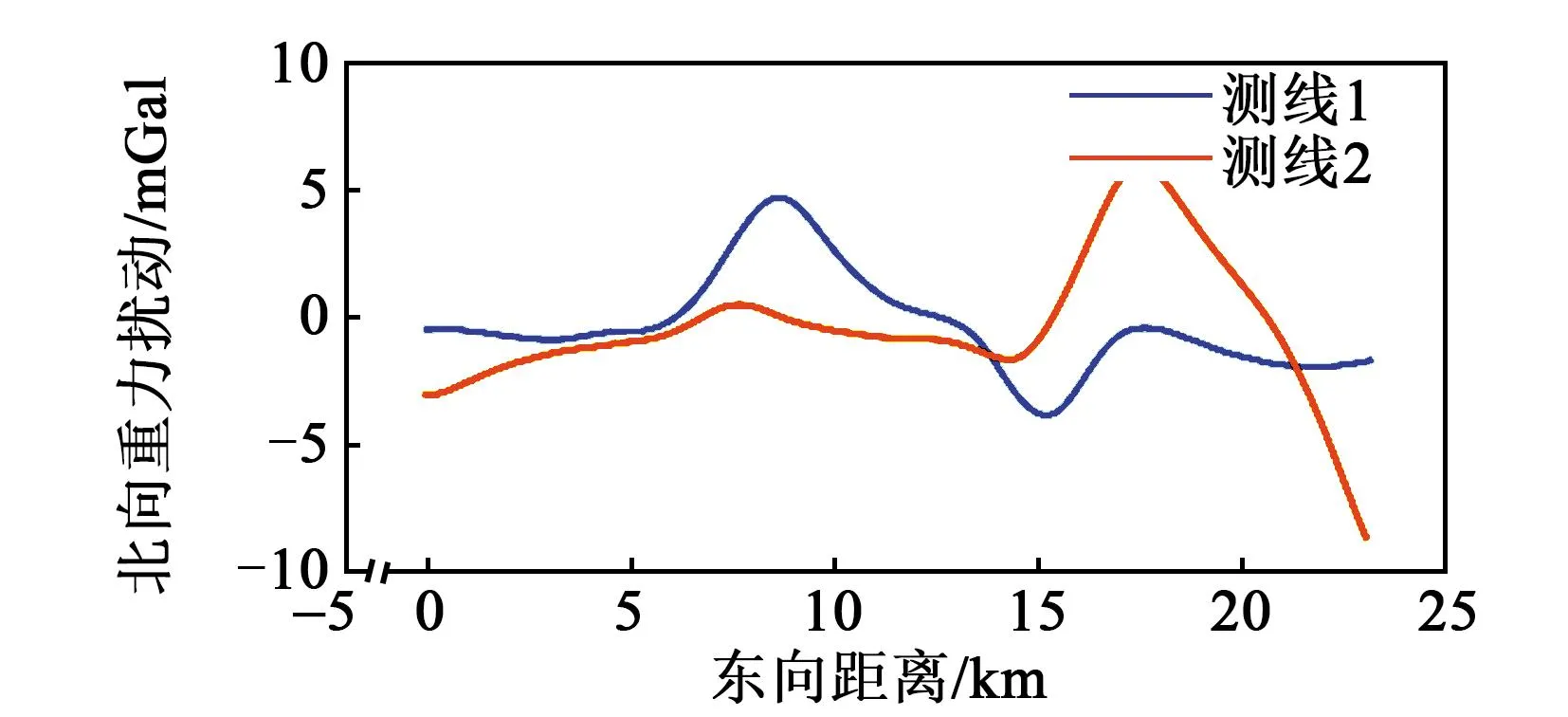
图4 两条东西向测线重力扰动矢量北向分量

两条南北向测线的重力扰动矢量水平分量计算结果如图5、6所示。由图可知,舰船在南北方向航行时,两条测线的东向和北向重力扰动重合情况较好,两条测线上的重力扰动水平分量存在的偏差在允许范围内,因此认为水平重力扰动能够从速度误差中分离出来。

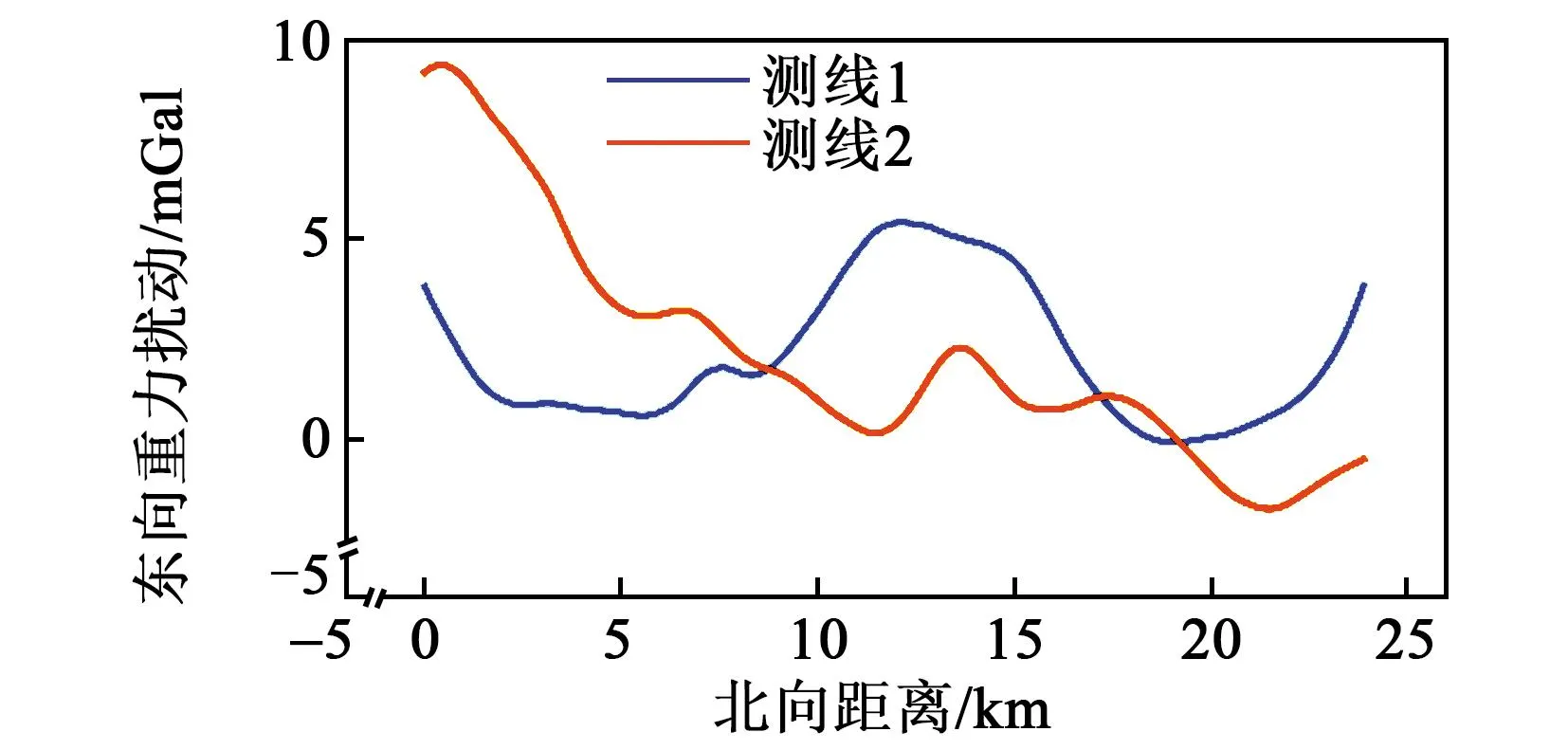
图5 两条南北向测线重力扰动矢量东向分量

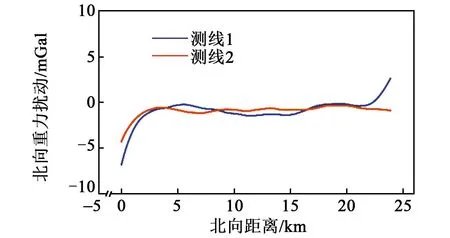
图6 两条南北向测线重力扰动矢量北向分量

两组测线的东向、北向重力扰动矢量的重复线精度如表1所示。

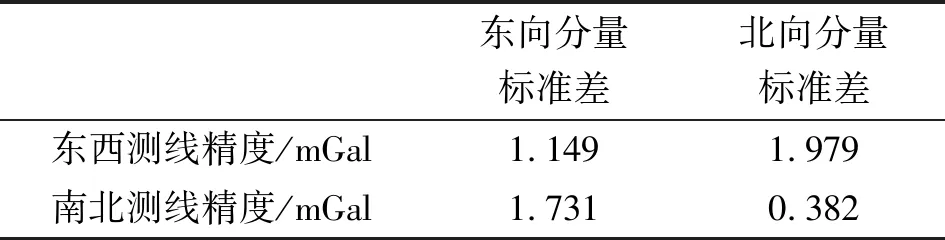
表1 两组重复测线的重力扰动的重复线精度

4 结束语

海洋重力矢量测量采用两步法估计重力扰动矢量水平分量。第一步采用高精度捷联惯导算法和扩展卡尔曼滤波对加速度计偏差进行了估计和补偿,获得计算导航系中的比力。第二步构建了重力扰动矢量水平分量的计算方程,将重力扰动矢量的水平分量建模为二阶高斯-马尔可夫随机过程,并利用正向-平滑的卡尔曼滤波,以分离加速度计偏差和重力扰动水平分量。其他重力扰动水平分量的求解方法均为一步法,水平重力扰动根据SINS/GNSS组合系统的卡尔曼滤波结果直接计算。但加速度计偏差和姿态误差角在估计过程中是耦合的,通过一步法不能有效区分。对实验数据的处理结果表明本文所提方法有效。