改进N-K 模型分析装配式建筑多阶段质量风险耦合

摘 要：为探究装配式建筑多阶段质量风险因素间的耦合机制，促进装配式建筑质量的提升，采用改进的N-K 模型计算耦合风险的大小. 在归纳总结样本文献基础上构建多阶段多层次的风险指标体系，依次采用主观赋权的AHP 法、客观赋权的惩罚-激励型变权综合评估法及拉格朗日乘子组合赋权法计算指标权重，并以权重代替概率方式对传统耦合模型进行改进，将203 篇有关装配式建筑质量风险样本文献统计数据进行耦合风险值的计算，结果表明： 风险耦合值的大小与参与耦合的风险因素个数成正相关；客观因素和主观因素结合后风险耦合值更大，更容易导致安全事故的发生；风险具有阶段间叠加传导的性质.

关键词：风险耦合；组合赋权；N-K 模型；耦合度

中图分类号：X947

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.09

装配式建筑相较于传统建筑具有减少污染、加快工期、高度信息化等优点，近年来发展装配式建筑已经上升为国家战略，政策支持力度不断增强.2016 年国务院《关于大力发展装配式建筑的指导意见》提出“力争用10 年左右的时间，使装配式建筑占新建建筑面积的比例达到30%”[1]；2017 年住建部《“十三五”装配式建筑行动方案》进一步明确装配式建筑占比目标等发展规划[2]；2022 年住建部发布《“十四五”建筑业发展规划》，要求到2035 年，迈入智能建造世界强国行列，提出装配式建筑是重点发展方向[3].

N-K 模型是研究系统中耦合效应的主流模型，其优越性在于能够相对简单的处理一些无法用传统方法解决的复杂问题[4]，如导致事故发生的因素发生耦合时对事故总体的影响效应. 此外，N-K 模型在分析已发生事故的客观数据时，可以降低主观偏见[5]，更客观地分析数据. 该模型应用领域广泛.例如，在施工安全领域，吴贤国等[6]在地铁施工安全风险管理领域，通过构建N-K 模型研究风险概率变化情况，对各因素的耦合影响水平进行了评价；方俊等[7]基于N-K 模型的耦合效应度量模型，进行耦合信息交互、耦合效应量化计算，并验证该模型的有效性和准确性；Guo[8]等在研究复杂地质和施工隧道风险时引入N-K 模型和耦合模型，度量耦合风险对施工的影响，分析风险耦合与各风险分量之间的关联机理. 在交通安全领域，杨婷等[9]应用NK模型分析危险品运输系统耦合风险，通过量化耦合风险值，使得风险大小比较更为直观；Zhang 等[10]将智能船舶的航行风险分为四个模块，结合299 条海事事故统计数据匹配智能船风险因素进行N-K模型的案例研究，为海上智能船的风险防范和管理提供理论和实践支撑；潘丹等[11]将飞机安全风险运行系统分为6 个风险子系统，并采用N-K 模型进行风险耦合的分析，为我国民航安全运行提供了理论支撑.

装配式建筑不同于传统的建筑，影响其质量的风险因素多且存在相互关联性，以往的文献只是简单地列举影响装配式建筑质量的风险因素，并未考虑多因素间耦合产生的影响. 基于此，本文从因素间相互关联性出发，考虑装配式建筑发生质量事故时情况复杂，现阶段无详细记录数据，采用拉格朗日乘子法计算的综合权重对传统N-K 模型进行改进，以弥补该模型的使用局限性，可以更科学系统地对装配式建筑质量事故进行分析.

1 风险指标建立及耦合机理分析

1.1 装配式建筑质量风险指标的建立

随着技术与管理的不断进步，发表较早的文献所提风险因素可能已不具备参考价值，因此收集2016—2023 年发表的文献作为样本文献，筛选总结事故发生的原因，利用改进的N-K 耦合模型对不同风险因素之间的作用程度进行计算，其计算结果可量化不同风险因素耦合度的大小.

为构建可用于分析装配式建筑质量风险的数据库，样本收集整理流程如下： （1）通过知网检索入口，设置检索项为“主题”，输入“装配式建筑＆质量风险”等词语，利用知网可视化功能的“文献互引分析”与“关键词共现网络分析”，统计得到2016—2023 年共208 篇有关装配式建筑质量风险的文献. （2）对样本文献进行筛选，确定有用样本文献为203 篇. （3）通过对203 篇样本文献中出现的质量风险进行统计分析，从“人、机、料、法、环”5 类因素进行识别，得到一个包含三类空间下的5 类一级指标、56 类二级指标的质量风险体系，如表1 所示.

1.2 装配式建筑质量风险耦合机理分析

“耦合”（coupling）是来自物理学的一个名词，定义为“两个或两个以上的体系或运动形式之间通过各种相互作用而彼此影响以致联合起来的现象”[12].耦合现象是客观、普遍存在的，在风险管理领域，风险耦合定义为“系统中风险因素间会产生相互激励或相互抵消的作用，导致风险事件发生概率增加或减少”[13]. 在装配式建筑作业过程中，涉及的质量风险空间分布广且关系错综复杂，若忽略风险之间的相关性即多因素耦合，则会使得风险决策过于理想化. 因此，要分析装配式建筑作业空间内质量风险耦合机理，为更直观地展示系统在受到外界扰动时质量风险因素的动态变化过程，基于耦合触发器原理分析装配式建筑质量风险递次演化过程[14]，针对装配式建筑的特性在传统耦合触发器理论基础上对耦合触发器进行改进，如图1 所示.

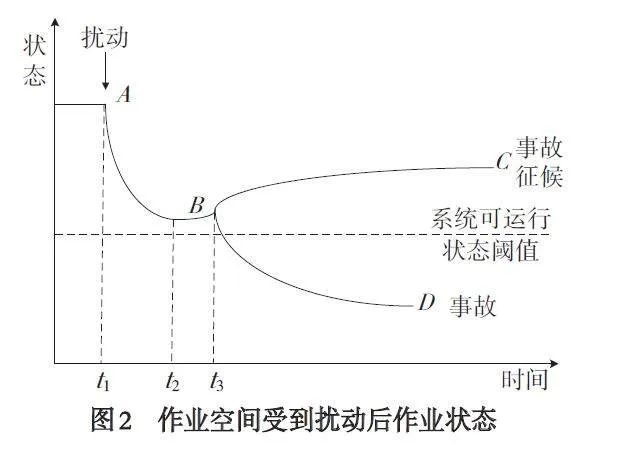
利用脆弱性理论分析因素耦合作用程度的方法[15]，对装配式建筑质量安全系统受到外界扰动后作业状态进行分析（图2），其中，R（t ） 1为t1 时刻受到外界扰动影响的质量安全性脉冲，R（t ） 2为t2 时刻适应度下的脉冲，R（t ） 3为t3 时刻冲破阈值后总防御系统脉冲. 在受到风险扰动后，A 点适应度出现，t 1、t2 时子防御系统开始发挥作用并达到系统运行最低点B，总防御系统在t3 时发挥作用，如果总防御系统较好，风险未冲破阈值，则系统运行状态为C. 反之为运行状态D.

2 指标赋权及耦合模型构建

2.1 指标权重的确定

在计算指标权重过程中，相关领域专家的意见对于指标权重评价结果具有重要意义，但受研究领域、个人偏向、专家数量等因素的影响，权重结果会有不同的误差. 而客观赋权法计算权重虽然可以避免受主观臆断影响，但计算方法的局限性及数据的科学性等因素也会限制权重的计算. 为使权重计算结果更加科学，本文在采用主观赋权和客观赋权得到指标权重的基础上，引入拉格朗日乘子法计算指标的综合权重，使得权重值更符合实际.

（1）层次分析法. 该方法考虑到决策者的主观臆断，计算简便且应用领域广泛. 其详细步骤可参考文献[16]，常权权重记为w 0i .

（2）变权理论. 根据变权原理，引入局部惩罚-激励型变权函数[17]，即

其中：γ 为惩罚水平，δ 为激励水平；d 0、d 1、d2 为评价策略；c 为调整系数；xi 为对第i 个指标的评估值. 惩罚-激励型变权函数曲线共分为三大区间，惩罚区间（0，γ ]、合格区间（ γ，δ ]、激励区间（ δ，1），其中惩罚区间（0，γ ]又分为轻度惩罚区间（0，α ]、中度惩罚区间（α， β ]、重度惩罚区间（ β，γ ]三类.

根据系统动力学中耦合状态的等级划分，耦合度Cm ∈ [ 0，1]，当Cm ∈ [ 0，0.3） 时，为弱耦合；当Cm ∈ [ 0.3，0.5） 时，为中耦合；当Cm ∈ [ 0.5，1]时，为强耦合[19].

3 应用案例分析

3.1 权重计算

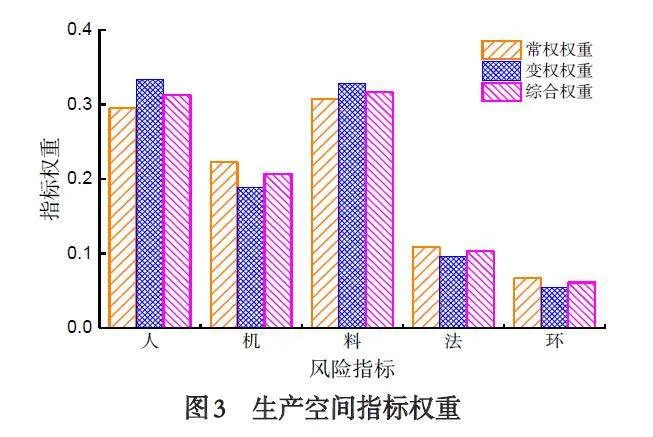
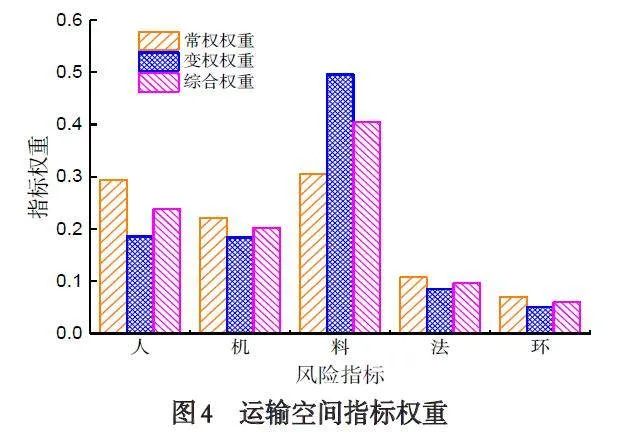
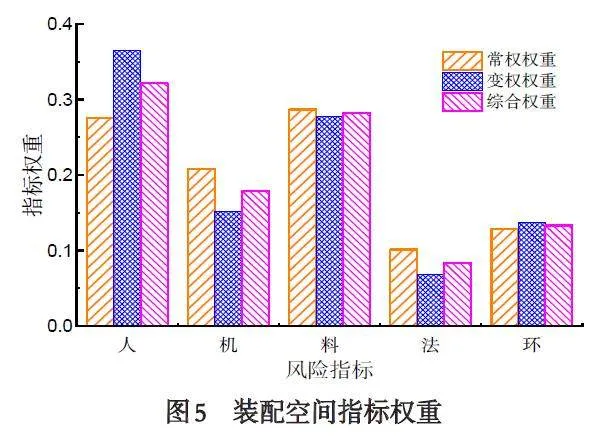
通过调查问卷收集该领域多位专家的意见与经验，分别对三个作业空间下质量风险指标进行评价打分后，利用AHP 法和变权理论分别得到指标的常权权重和变权权重，然后通过拉格朗日乘子法得到综合权重，三种方法计算得到权重结果见图3、4、5.

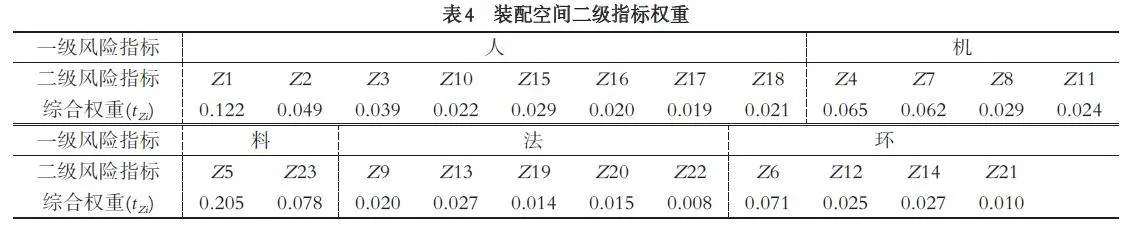
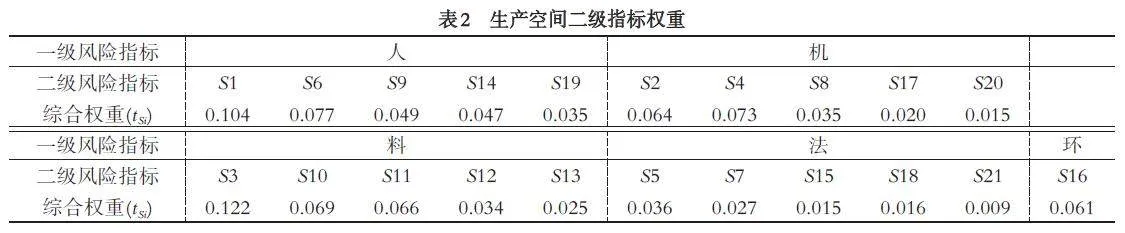
综合权重法得到的不同作业空间下二级风险指标权重结果（表2、3、4）.

根据表2 至表4 的权重数据分别计算三个空间中不同风险耦合的频度，例如生产空间中，“人因层”单一因素耦合频度为，PS10000 = t1 （t6 + t9 + t14 +t19 ） + t6 （t9 + t14 + t19 ） + t9 （t14 + t19 ） + t14∙t19 = 0.118；“人-机”双因素耦合频度情况为，PS11000 = （t1 + t6 +t9 + t14 + t19 ）（t2 + t4 + t8 + t17 + t20 ） = 0.025；“ 人-机-料”三因素耦合频度情况为，PS11100 = （t1 + t6 +t9 + t14 + t19 ）（t2 + t4 + t8 + t17 + t20 ）（t3 + t10 + t11 +t12 + t13 ） = 0.059；“人-机-料-法”四因素耦合频度情况为PS11110 = （t1 + t6 + t9 + t14 + t19 ）（t2 + t4 + t8 +t17 + t20 ）（t3 + t10 + t11 + t12 + t13 ）（t5 + t7 + t15 + t18 +t21 ） = 0.006，同理可得其他作业空间风险因素耦合频度数据. 在实际案例统计时，风险耦合频率等于案例中每种耦合情况出现的次数与全部案例次数之比，频率和为1，因此将计算结果进行归一化处理.

3.2 耦合计算

分别从三个作业空间下的人因层、设备层、物料层、管理层、环境层，分析质量风险因素耦合作用程度对装配式建筑质量的影响，并采用权重代替概率的方式计算风险耦合结果. 在N-K 风险耦合模型中，为计算T，先计算各耦合风险发生的概率，用“0”和“1”分别表示风险因素未发生耦合和发生耦合的情况，“∙”表示对该因素状态不做约束. 以生产空间为例计算因素耦合概率：

（1）单因素耦合概率. 人员因素不参与风险耦合时的概率为：

P0∙∙∙∙ = P01000 + P00100 + P00010 + P00001 + P01100 + P01010+P01001 + P00110 + P00101 + P00011 + P01110+P01101 + P00111 + P01011 + P01111 = 0.4575

同理可得其他单因素耦合概率，结果如表5 所示，且满足P0∙∙∙∙ + P1∙∙∙∙ = 1.

（2）双因素耦合概率. 人员因素和设备因素不参与风险耦合时的概率为：

P00∙∙∙ = P00100 + P00010 + P00001 + P00110+P00101 + P00011 + P00111 = 0.2561

同理可得其他双因素耦合概率，结果如表6 所示，且满足P00∙∙∙ + P11∙∙∙ + P01∙∙∙ + P10∙∙∙ = 1

（3）三因素耦合概率. 人员因素、设备因素及材料因素不参与风险耦合时的概率为：

P000∙∙ = P00001 + P00010 + P00011 = 0.1123

同理可得其他三因素耦合概率，且满足P000∙∙ +P001∙∙ + P010∙∙ + P100∙∙ + P011∙∙ + P101∙∙ + P110∙∙ +P111∙∙ = 1.

（4）四因素耦合概率. “ 人、机、料、法”因素不参与风险耦合时的概率为：

P0000. = P00000 + P00001 = 0.0961

同理可得其他四因素耦合概率，且满足P0000∙ + P0001∙ + P0010∙ + P0100∙ + P1000∙ + P0011∙ +P0101∙ + P1001∙ + P0110∙ + P1010∙ + P1100∙ + P1110∙ +P1101∙ + P1011∙ + P0111∙ + P1111∙ = 1

（5）五因素耦合概率. 同理可得五因素耦合情况，且满足

P00000 + P10000 + P01000 + P00100 + P00010 + P00001 +P11000 + P10100 + P10010 + P10001 + P01100 + P01010 +P01001 + P00110 + P00101 + P00011 + P11100 + P11010 +P11001 + P10110 + P10101 + P10011 + P01110 + P01101 +P01011 + P00111 + P11110 + P11101 + P11011 + P10111 +P01111 + P11111 = 1

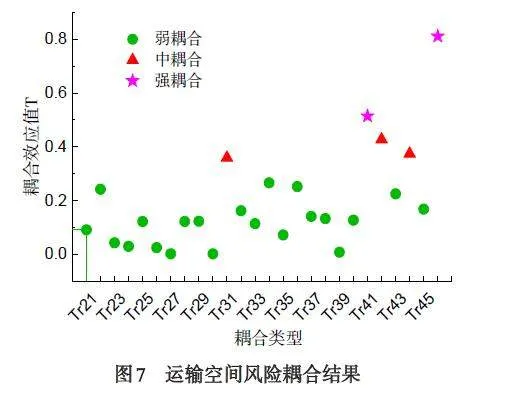
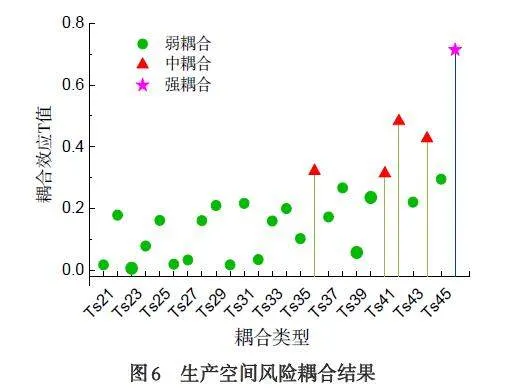
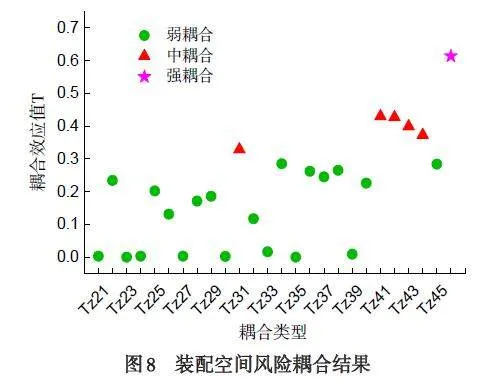
将不同耦合类型下的耦合概率代入对应耦合模型公式中，得到不同风险耦合结果如图6 所示，同理可得其他作业空间风险耦合结果（图7-图8）.

3.3 结果分析

结合图6-图8可知，排名前20的T 值大小排序为：

TR5（a，b，c，d，e ） gt; TS5（a，b，c，d，e ） gt; TZ5（a，b，c，d，e ） gt; TR41（a，b，c，d ） gt;TS42（a，b，c，e ） gt; TZ41（a，b，c，d ） gt; TS44（a，c，d，e ） = TR42（a，b，c，e ） =TZ42（a，b，c，e ） gt; TZ43（a，b，d，e ） gt; TR44（a，c，d，e ） gt; TZ44（a，c，d，e ） gt;TR31（a，b，c，d，e ） gt; TZ31（a，b，c ） gt; TS36（a，c，e ） gt; TS41（a，b，c，d ） gt;TS45（b，c，d，e ） gt; TS34（a，c，d ） gt; TZ45（b，c，d，e ） gt; TR34（a，c，d ）

结合风险耦合效应度量计算和耦合交互组合类型，各因素耦合结果分析如下：

（1）在三个作业空间中，强耦合均为多因素耦合交互类型；中耦合大部分为四因素耦合交互类型；而三因素和双因素耦合交互类型多为弱耦合. 由此可见，风险耦合度值大小与参与耦合的风险因素个数成正比.

（2）在排名前20 的T 值中，生产空间与运输空间的风险耦合类型均包含人员因素和材料因素，说明“人”和“料”的因素最易与其他因素耦合；而装配空间的风险耦合类型出现“人、机、料”因素的概率较大，说明在该空间内这三类因素最易与其他因素耦合.

（3）相较于其他两个作业空间，装配空间风险耦合度结果整体偏高，说明该空间风险因素发生耦合时对装配式建筑质量安全系统影响最大.

4 结论与建议

本文以2016—2023 年作为文献检索时间段，从知网上检索到203 篇有关“装配式建筑质量风险”文献作为样本文献，从全过程的角度将其分为三个作业空间进行风险因素分析，并运用组合赋权法计算风险的出现频率，来确定某一风险因素在装配式建筑质量风险事件中发生的频度. 构建了基于组合赋权法的装配式建筑质量风险N-K 模型. 改进后的N-K 模型在无法获得大量事故统计数据概率的情况下，通过拉格朗日乘子法计算风险因素综合权重，可以得到风险因素在事故中发生的频度并进行风险耦合分析，该方法弥补了传统N-K 模型的适用局限性. 基于改进后的N-K 模型计算装配式建筑质量风险耦合结果分析：所有作业空间内强耦合都为多因素耦合类型，且耦合度T 值随着多因素耦合中因素数量的增多，逐渐增大，T 越大事故发生的隐患就越大；在任意一个作业空间内人员因素及材料因素都显得格外活跃，且各因素耦合类型中主观因素与客观因素关联性更密切；质量风险以PC 构件为载体，通过在生产空间及运输空间内耦合、叠加、传导，导致装配空间质量风险耦合度最高. 基于上述结果对装配式建筑质量安全提出以下建议： 第一，在装配式作业空间中人员作为一种主观因素具有主观能动性，提高人员素质、规范人员行为是保证建筑质量安全性的重要保障. 第二，PC 构件的生产、运输、吊装都需提前做好应对突发状况的方案，保证工作环节顺畅，避免赶工造成的建筑质量问题. 第三，当某一作业空间内出现质量风险问题时应及时补救，以免风险通过PC 构件叠加、传导至下一作业空间，造成更大的经济损失. 第四，尽可能避免多因素的耦合，尤其是客观因素与主观因素的耦合.

参考文献：

[1] 中华人民共和国国务院办公厅. 国务院办公厅印发《关于大力发展装配式建筑的指导意见》的通知： 国办发〔2016〕71 号[EB/OL]. （2016-09-30） [2023-11-24]. https：//www.gov.cn/xinwen/2016-09/30/content_5114334.htm.

[2] 住房和城乡建设部. 住房和城乡建设部关于印发《“十三五”装配式建筑行动方案》的通知：建科〔2017〕77号[EB/OL]. （2017-03-23）[2023-11-24]. https：//www.mohurd.gov.cn/gongkai/zhengce/zhengcefilelib/201703/20170329_231283.html.

[3] 住房和城乡建设部. 住房和城乡建设部关于印发“十四五”建筑业发展规划的通知： 建市〔2022〕11 号[EB/OL]. （2022-01-25） [2023-11-24]. https：//www. mohurd. gov. cn/gong⁃kai/zhengce/zhengcefilelib/202201/20220125_764285.html.

[4] GANCO M， HOETKER G. NK modeling methodology inthe strategy literature： bounded search on a rugged landscape[M]//Bergh D D， Ketchen D J. Research Methodology inStrategy and Management， Leeds： Emerald Group PublishingLimited， 2009： 237-268. doi： 10.1108/s1479-8387（2009）0000005010.

[5] 周红波， 杨奇， 杨振国， 等. 基于复杂网络和N-K 模型的塔吊安全风险因素分析与控制[J]. 安全与环境学报， 2020， 20（3）： 816-823.

[6] 吴贤国， 吴克宝， 沈梅芳， 等. 基于N-K 模型的地铁施工安全风险耦合研究[J]. 中国安全科学学报， 2016， 26（4）： 96-101.

[7] 方俊， 郭佩文， 朱科， 等. 基于N-K 模型的地铁隧道施工安全风险耦合演化分析[J]. 中国安全科学学报， 2022， 32（6）：1-9.

[8] GUO D， SONG Z， XU T， et al. Coupling analysis of tunnelconstruction risk in complex geology and construction factors[J].Journal of Construction Engineering and Management， 2022（9）：1943-7862. doi：10.1061/（ASCE）CO.1943-7862.0002360.

[9] 杨婷， 帅斌， 黄文成. 基于N-K 模型的道路危险品运输系统耦合风险分析[J]. 中国安全科学学报， 2019， 29（9）：132-137.

[10] ZHANG W， ZHANG Y. Research on coupling mechanismof intelligent ship navigation risk factors based on N-K model[J]. Journal of Marine Science and Technology， 2023， 28（1）：195-207. doi：10.1007/s00773-022-00919-0.

[11] 潘丹， 李永周， 罗帆. 基于N-K 模型的飞机运行安全风险耦合研究[J]. 安全与环境学报， 2022， 22（2）： 606-614.

[12] 王念纤. 我国科技创新与产业发展的耦合机制研究[D]. 保定： 河北大学， 2018.

[13] 李小雪， 雷可， 谭忠盛， 等. 城市地下空间施工风险因素耦合效应研究[J]. 土木工程学报， 2021， 54（S1）： 76-86.

[14] 黄文成， 帅斌， 孙妍. 基于N-K 模型的铁路危险品运输系统耦合风险形成机理研究[J]. 铁道学报， 2019， 41（5）： 1-9.

[15] 李德清， 崔红梅， 李洪兴. 基于层次变权的多因素决策[J].系统工程学报， 2004（3）： 258-263.

[16] 马子媛， 李海莲， 蔺望东. 基于层次变权未确知理论的沥青路面预养护评价模型[J]. 合肥工业大学学报（自然科学版），2021， 44（12）： 1668-1675.

[17] 段树乔. 电力企业安全管理变权综合评价方法[J]. 数学的实践与认识， 2003（8）： 17-23.

[18] 杨锡运， 刘欢， 张彬， 等. 基组合权重相似日选取方法及光伏输出功率预测[J]. 电力自动化设备， 2014， 34（9）：118-122.

[19] 胡立伟， 薛宇， 赵雪亭， 等. 驾驶员不同驾龄条件下公路交通风险致因耦合影响研究[J]. 安全与环境学报， 2023， 30（2）： 1-9.

【编校：许洁】

基金项目：国家自然科学基金青年项目（72204001）；安徽省高校人文社科重大项目（SK2021ZD0035）；复杂系统多学科与控制安徽省教育厅重点实验室开放课题项目（RZ2200000691）