基于Serpenoid曲线的多关节仿生机器人设计与实验测试

卢亚平， 宋天麟， 王日禾

（苏州大学应用技术学院，江苏 苏州 215325）

0 引言

多关节仿生机器人研究是目前仿生机器人领域中比较活跃的一个方向，多关节机器人研制，已成为仿生领域的研究热点。像机械昆虫、机器鱼、机械狗、机械蛇、毛毛虫等多关节仿生机器人，都有着独特的运动方式，每种运动方式都有着它一定的应用价值，研究多关节机器人运动方式有着重要意义。蛇是一种极为特殊的生物，它的运动形式非常的特别，吸引着众多科学家的研究兴趣。本设计结合蛇类的蜿蜒运动，实现多关节仿生机器人的仿生运动姿态，达到机器人仿生运动控制的要求［1］。

1 Serpenoid曲线

考虑机器人运动的仿生性，设计选择蜿蜒的运动方式，并假设是正弦波的传递，由此计算出波形传递过程中各个关节相对旋转角度的变化，从而控制波形稳定的向前推进。由于多关节机器人类似一个多连杆系统，通过各相邻连杆的协调动作向前推进。设计以Serpenoid曲线为例对多关节机器人的运动步态进行规划，Serpenoid 是一个通过X-Y坐标原点的蜿蜒曲线［2-3］：

式中：α为曲线的摆动幅度；β 为单元长度内波形的周期数；c为波形的偏移角。通过改变Serpenoid 曲线的3 个参数，既可改变蜿蜒曲线波形的传播幅度、曲线的频率，还可改变曲线的偏移角度，即曲线的传播方向。由Serpenoid曲线定义，可计算得出N关节组成的近似Serpenoid曲线蛇型机器人蜿蜒运动的角度［4］。

2 机械结构设计

使用solidworks软件模拟生物蛇骨架，设计仿生机器人三维模型，设计有1 个头部关节，7 个身部关节，1 个尾部关节。舵机作为驱动元件连接各关节。通过舵机的控制带动各关节的摆动，依靠与地面间的摩擦力驱动机器人移动。头部关节分为上下板结构，上板放置传感器模块，下板放置主控板。身部关节固定舵机和连接其他关节，舵机作为关节摆动的执行器件，通过紧固件装配在身部关节的舵机定位孔上。尾部关节安装电池，为机器人控制系统提供动力［5］。设计方案如图1 所示。

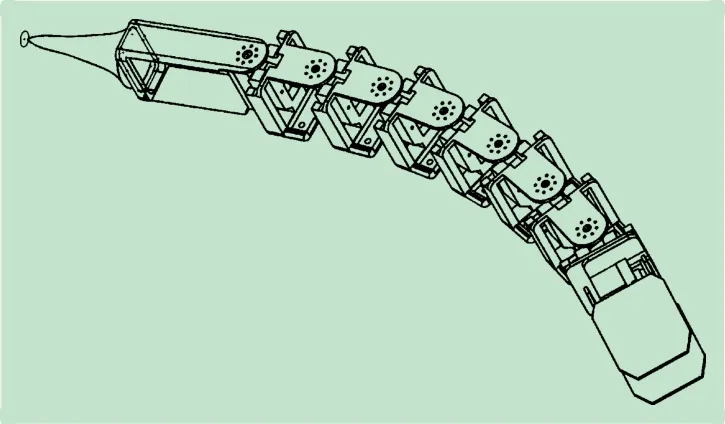
图1 整体结构设计模型

3 身部关节应力测试

应力测试主要分析身部关节上半部位折弯处的强度。在身部关节舵机头连接处施加50 N 的向下压力载荷。在向下压力作用下，前端臂梁向下弯曲，发生静态位移，前端位移量为9.5 mm。整体Von Mises应力状态如图2 所示，由施压后得到应力云图，可以看出最大的受力值以及最危险的红色区域。由图可见，臂梁右侧直角折弯处的红色部分内应力最大，形变也最大。由此在3D打印制作过程中需加固，在舵机头连接处右侧直角折弯处，增加圆弧过渡，使身部关节的臂梁不易折断［6-7］。

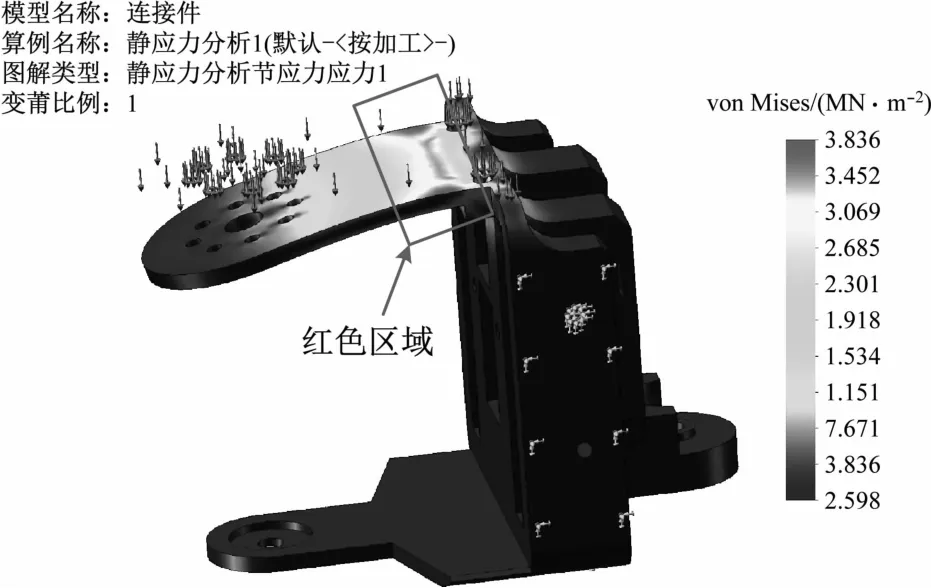
图2 冯米斯应力（Von Mises）分布

4 系统框架设计

系统设计框图如图3 所示，STM32 作为机器人核心控制器，连接各类传感器，实现仿生设计理念和环境监测多样性。机器人采用超声波模块，模仿人的眼睛，实现环境侦察功能；采用人体红外传感器，模仿人的感官，实现生物监测功能；采用声音传感器，模仿人的耳朵，实现声音监测功能［8］。

图3 系统控制设计框图

5 控制方法设计

步态运动采用7 个关节（θ1～θ7）来实现。通过计算得出任一时刻舵机的运动角度，对照角度表编程控制每个关节舵机运动角度，实现对应的运动步态。机器人不断扫描检测声音信号和人体感应信号，当信号强度超过设定的阈值后，系统进入潜伏模式或蜷缩模式。声音信号作为潜伏模式的依据，人体感应信号作为蜷缩模式的依据［9］。控制流程图如图4 所示。

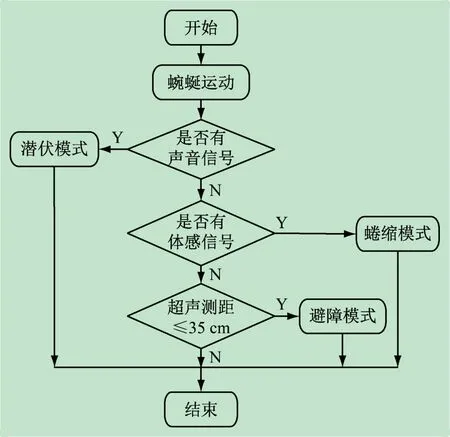
图4 多关节仿生机器人控制流程图

潜伏模式：各关节舵机角度保持为0°，使机器人呈现出一条直线，且头部在头关节舵机驱动下伏于地面，不易被发现。

蜷缩模式：各关节舵机角度统一方向摆动34°，各关节蜷缩在一起，但头部舵机驱动一定角度，模仿蛇类生物头部昂起的动作，使得机器人施展空间最小化。

避障模式：以右侧转弯为最优原则，进行机器人的运动避障。

5.1 蜿蜒运动步态

蛇类运动步态中，图5 中给出了完整的多关节蛇类运动步态。从头部开始，身部关节借助腹部与地面之间的摩擦力完成蜿蜒运动；结合观察蛇类的运动姿态，利用Serpenoid曲线运动计算出重要姿态时的各舵机角度，并建立各时刻舵机的角度表。对照角度表编程控制每个关节舵机运动角度，实现对应的运动步态。并通过舵机（θ2、θ1）的角度控制，实现在蛇类运动中转向。运动中，关节（θ7～θ3）起主要推力作用，关节（θ2、θ1）起导向作用［10-11］。

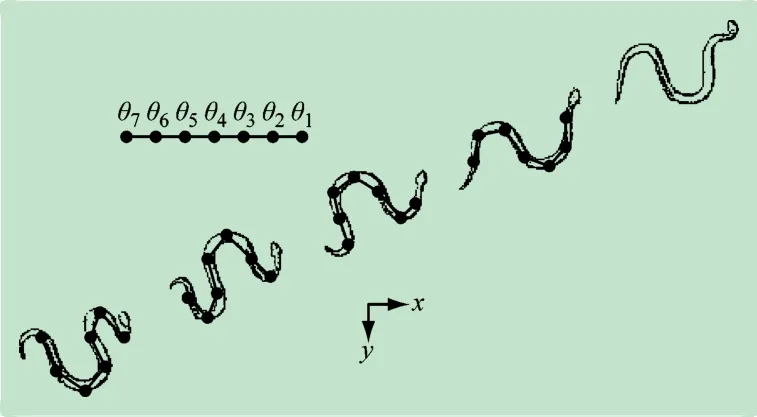
图5 蛇类运动步态

5.2 关节角度数据

依据前期蛇类蜿蜒运动步态的研究，将Serpenoid曲线运动公式导入Matlab 软件，进行轨迹运动仿真。如图6 所示，各关节模拟仿真出t0～t10时刻的运动轨迹，以此设计程序。在实际调试过程中，为不仅让机器人运动姿态接近于蛇类运动形态，并产生有效的距离移动，会对各关节角度的大小进一步的微调［12］。

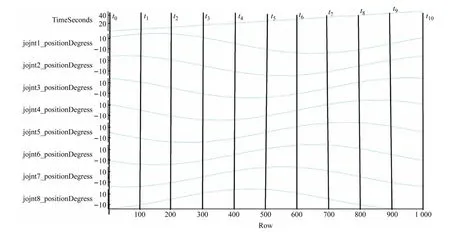
图6 t时刻各舵机蜿蜒运动波形

依据t0～t10时刻的角度大小，编写角度数据表，见表1。通过角度换算成脉宽信号，输入控制器。表1数据呈Serpenoid曲线规律性变化，纵向：单个关节舵机角度数据以类似正弦波形变化；横向：8 个关节舵机角度数据实现左偏移。纵横结合实现运动波形的传递，实现蜿蜒运动步态［13-14］。

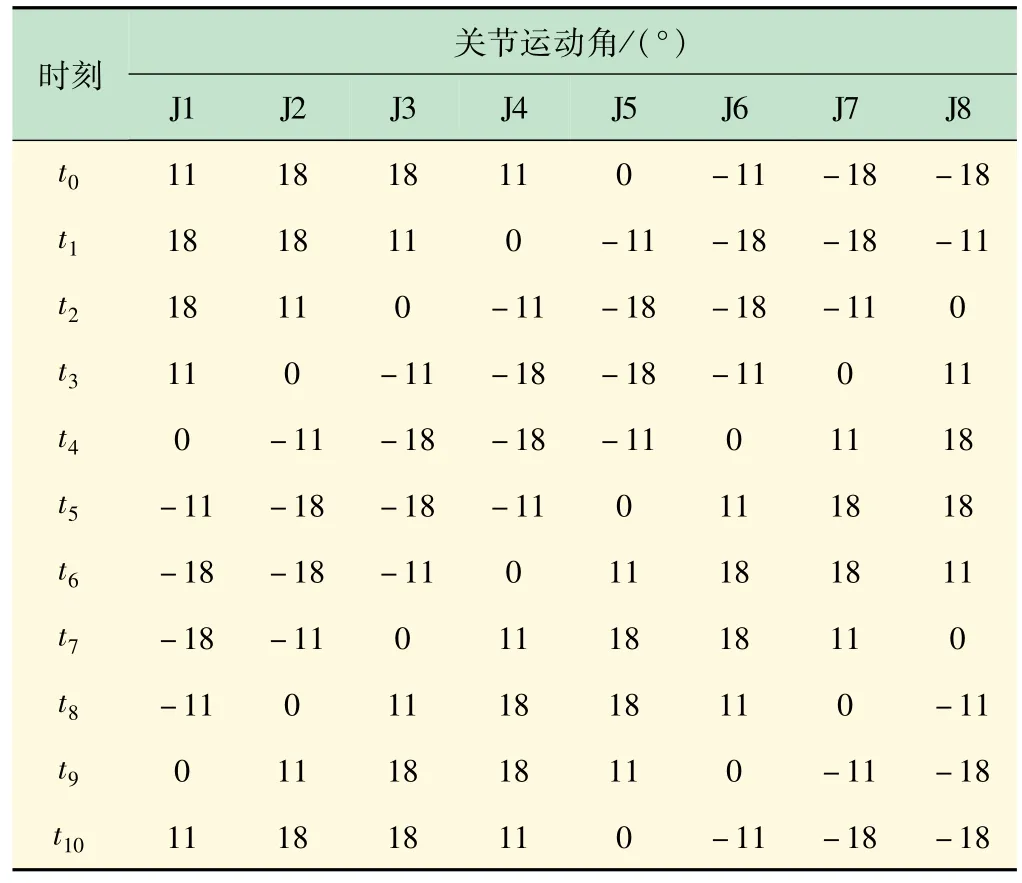
表1 蜿蜒运动角度数据

5.3 姿态角度编程

在机器人蜿蜒运动姿态编程，机器人通过舵机的摆动带动身部关节的腹部与地面摩擦前进。依据表1的角度数据编写舵机摆动程序，程序对8 个舵机角度做等值比较，以准确判断舵机角度是否转动到设定值。程序中设置有11 个条件，循环顺序为：t0→t1→t2→t3→t4→t5→t6→t7→t8→t9→t10。

流程如图7 所示，设置11 个阶段，以分解蜿蜒运动中各阶段机器人舵机的角度，通过switch（temp）语句来进行顺序选择，当temp ＝0 时，执行t0时刻的各舵机PWM数据；当temp ＝1 时，执行t1时刻的各舵机PWM数据，依次类推，通过分阶段的组合实现蜿蜒运动。其中蜿蜒运动的前进与后退的角度为相反关系，即t0～t10时刻顺序为前进，而t10～t0时刻顺序为后退［15-16］。

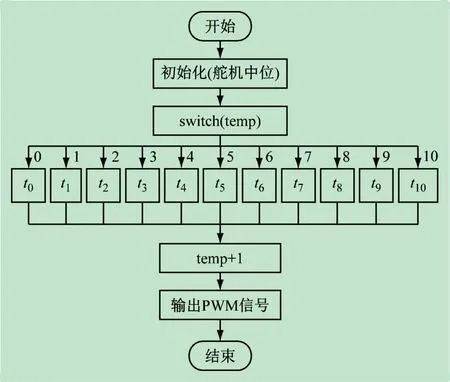
图7 t时刻角度编程流程图

6 Sim运动仿真测试

通过CoppeliaSim机器人仿真平台，构建仿生机器蛇模型，如图8 所示，并使用c语言编程描述控制机器人运动。

图8 Sim运动仿真中的模型

6.1 参数α对运动的影响

根据蛇类蜿蜒运动时关节随时间变化关系

建立仿真程序脚本。仿真环境不考虑地面摩擦力影响。当取β ＝4π，c＝0 保持不变的情况下，分别令α ＝30 和60，得到如图9、10 所示的参数α 影响下的蛇形曲线［17-18］。

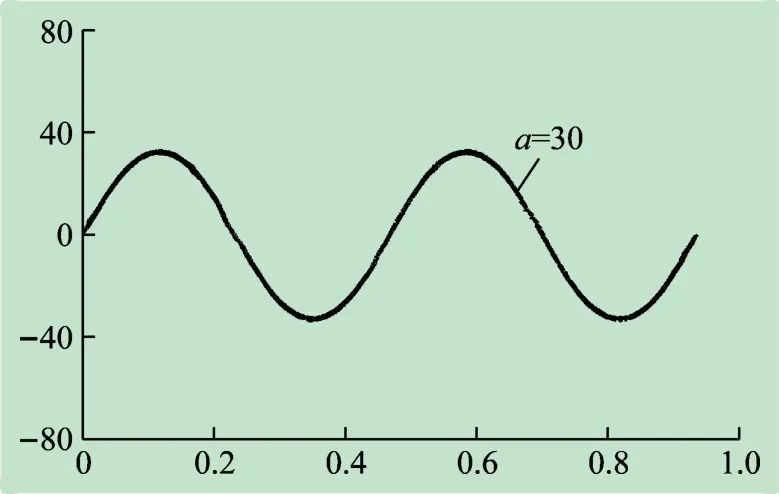
图9 α ＝30时关节变化曲线

图10 α ＝60时关节变化曲线

通过以上波形分析，单位波形的长度随着α 值的减小而增大；单位波形的幅值随着α 的减小而减小，由此可以看出α值越小，运动幅度越趋于平缓。

6.2 参数β 对运动的影响

当取α ＝30，c＝0 保持不变的情况下，分别令β ＝4π、8π。得到如图11、12 所示的参数β影响下的蛇形曲线。

图11 β ＝4π时关节变化曲线

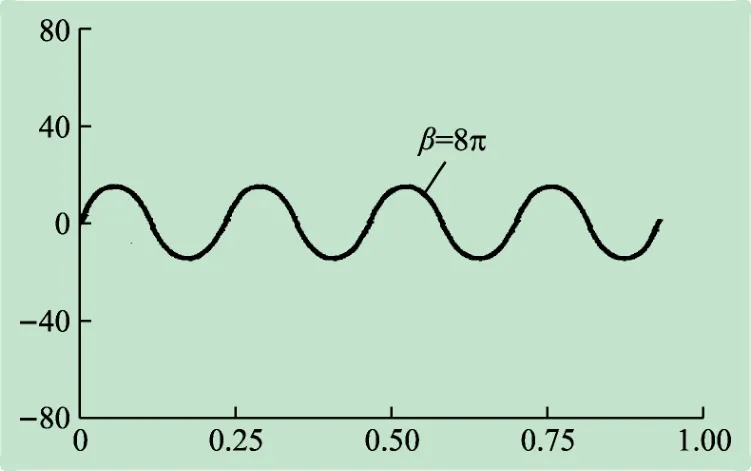
图12 β ＝8π时关节变化曲线

通过以上运动轨迹和关节变化曲线可以看出，当α值保持不变的情况下，β 值越大，单位曲线长度中正弦周期的个数随着β 值的增大而增大，而振幅随着周期个数的增多而减小。由此可见，β取值越大，整体摆动幅度越小，关节变化速度越快。α、β 参数影响着机器人整体的摆动幅度和关节变化速度，具体见表2。

表2 α、β 参数对运动的影响

7 蜿蜒运动实物测试

通过CoppeliaSim运动仿真，选用α、β参数进行编程。测试机器人底部摩擦方式对运动位移的影响，设计加工2 种运动模型（模型A 和模型B），如图13 所示。不同的摩擦方式对机器人的位移有着较大的影响，决定了是否能产生有效的前进推力。模型A 采用的是万向轮，实现机器人与地面的点摩擦；模型B 采用的是小滚轮，实现机器人与地面的线摩擦［19-20］。

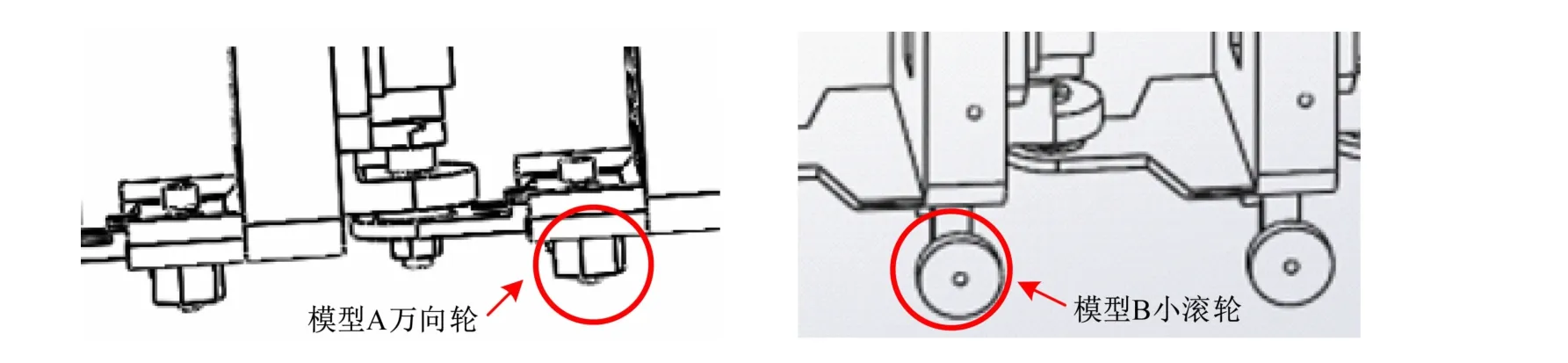
图13 模型A和模型B摩擦方式

测试过程中，不同模型配置不同的α、β 参数，以便比较结构设计不同、摩擦方式不同和运动参数不同对机器人运动带来的影响。测试中通过相机拍摄，得到大量机器人的蜿蜒运动图，机器人的蜿蜒动作实拍如图14、15 所示，机器人通过各关节进行蜿蜒运动，实现一定量的位移，由此分析不同的α、β 参数和不同的摩擦方式对机器人运动效能的影响。

图14 模型A蜿蜒测试

7.1 模型A蜿蜒测试

由仿真得知，α影响关节运动时摆动的平稳性（α越大，摆动幅度越大），β 影响整体摆动幅度和摆动速度（β取值越小，整体摆动幅度越大，关节变化速度越慢）。本次测试采用α ＝60，以提升摆动的幅度；β ＝8π，以降低整体摆动幅度，提高关节变化速度。

通过高清相机拍摄的大量图片发现，当α ＝60、β ＝8π时，单位时间内摆动频率较高，摆动幅度较大，导致机器人实际有效移动距离较小，大部分运动是无效运动，即为原地摆动。依图14 的测试情况测算得出：平均在0.5 s内摆动1.5 个周期。在8 s内移动了一个蛇身（约16 cm），平均移动速度2 cm／s，移动效率偏低。

7.2 模型B蜿蜒测试

模型B测试采用α ＝30，增大运动波形的长度，降低摆动的幅度，提高稳定性。采用β ＝4π，以提升整体摆动幅度，减小关节变化速度。

当α ＝30、β ＝4π 时，单位时间内摆动频率降低，摆动幅度稍微增大，实现机器人有效移动距离显著增加。依图15 测算得出：平均在2 s内摆动0.7 个周期，使得动作缓慢，但移动效果明显，柔性较好。在20 s内移动了90 cm，平均移动速度4.5 cm／s，且动作更具有蛇类运动的柔性效果。

图15 模型B蜿蜒测试

通过实测，A、B 模型配置不同的α、β 参数，其运动路径长度有显著差距，如图16 所示。模型B得到了最优平均路径长度，前进阻力有了大幅度的削减，证明了模型B的摩擦方式对路径导向性（刚性问题）和参数α、β对改进推进效率带来显著的成效。在时间相对较短的情况下，确保机器人各关节冲击不会产生较小的抖动现象，保证运动轨迹的平滑性。

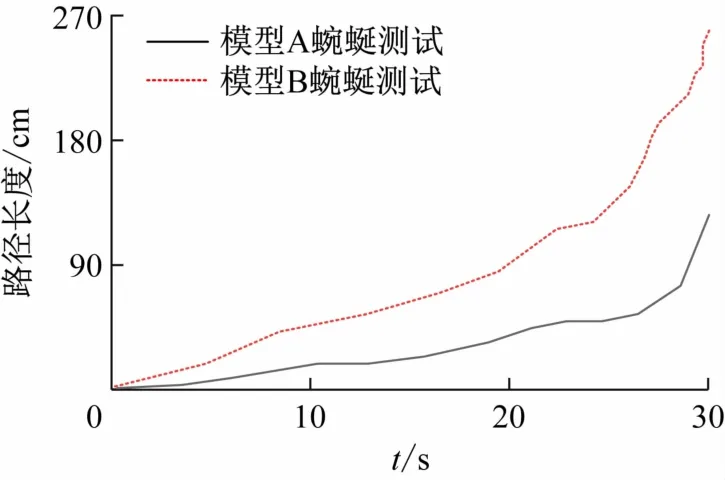
图16 时间与行走路径长度对应关系

7.3 实验测试分析

蜿蜒运动实验测试分析：较好的运动效果不仅需要选择合适的α、β 两参数的共同作用，还需要选择机器人与底部合适的运动摩擦方式。才能达到最佳效果，机器人推进成效更完美。

（1）蜿蜒运动。各关节的摆动频率，摆动幅度决定了机器人的运动效果。各关节角度的摆动频率和摆动幅度又因α、β 两参数的不同而改变。选择合适的α、β两参数，才能使机器人更加有效地进行蜿蜒前进。通过测试发现，当α ＝30、β ＝4π 时，能实现较好的位移，平均移动速度能到达4.5 cm／s，具有蛇类的仿生运动效果。

（2）模型设计。采用模型B 与模型A，设计不同的底部运动摩擦方式。测试发现在蜿蜒运动中，小滚轮具有较好的导向性，致使机器人在运动时各关节产生的推力较好的集中到一个方向上。而万向轮360°方向皆可，使力的作用较分散，机器人在运动时各关节产生的推力被万向轮分散，不易集中。

（3）关节组装。不仅要考虑关节连接处往复摩擦问题，还需考虑仿生设计效果，找到适合的外形结构设计也很重要。测试结果显示，使用轴承设计能够减少关节连接处的摩擦，使机器人各关节间的摆动具有较好的运动性。使用紧固件设计可较好的固定舵机，在运动过程中能较好地提供稳定动力。

8 结语

通过分析生物蛇骨架模型和运动步态，提出一种多关节仿生蛇形机器人结构方案。并在Serpenoid 数学模型基础上，通过对数学模型的仿真，总结了α、β两参数影响仿生机器人曲线运动的规律，并在仿生机器人样机上进行了试验。实验证明，机器人关节（θ2、θ1）对路径导向性（刚性）、参数α、β 对运动推进效率和底部摩擦方式对有效运动位移都有显著关联，对基于Serpenoid 曲线的仿生机器人的运动控制有重要意义。