时域有限差分方法分析水下目标散射电场分布

刘 健， 郭元龙， 张庆一， 魏宝君， 刘学锋， 王殿生

（中国石油大学（华东）理学院，山东 青岛 266580）

0 引言

随着水下电磁波通信和海洋勘探技术的发展，水下目标的电磁探测逐渐成为水下电磁场研究的重点方向。海水的高电导率，中高频电磁波在海水中传播具有极强的衰减效应［1］，研究低频电磁波在水下的传播和电磁散射问题愈发重要。目前解决水下电磁散射的计算方法主要有时域有限差分法（Finite Difference Time Domain，FDTD）［2］、矩量法［3］、体积分方程法［4］和有限元法［5］等。其中FDTD 方法凭借其计算全空间、全时段和大尺寸目标散射电场分布的快速以及能够通过傅里叶变换求解全频域散射结果，已发展成为研究水下电磁散射的常用方法［6］。FDTD 方法是通过将时域麦克斯韦旋度方程进行差分，得到电场强度和磁场强度满足的时空耦合离散的差分方程，通过迭代求解计算得到全空间电磁场分布［7-8］。在海水电磁场计算中，海水是有耗的色散介质，FDTD方法可在时域下求解色散介质瞬态电磁问题，故FDTD 方法在处理色散介质的电磁衰减并计算水下目标全空间瞬时散射电磁场方面具有优势。

国内外学者做了大量水下电磁波传播与散射电磁场分析计算的理论研究。在水下电磁波传播方面，Xia等［9］利用FDTD方法分析了湖水中低频电磁波的传播规律，验证了FDTD 方法计算水下电磁波传播的可行性。在电磁散射方面，Luebbers等［10］通过卷积递归法差分计算真空中频率相关材料的三维电磁散射场，为海水等色散介质中FDTD 计算提供了支持；郑奎松等［11］提出大比例网格变换的总场-散射场源时域FDTD方法，在二维空间计算水下油、气、水合物等高阻和金属等低阻物体模型的电磁散射，为利用FDTD方法计算水下电磁散射给予了参考。

由于海水和水下目标是色散介质，入射电磁波频率f和目标电导率σ 都会对实际水下探测产生影响，需对入射电磁波频率和水下目标材料电导率进行系统性对比研究。基于上述考虑，在前人研究的基础上，构建三维海水色散介质的时域有限差分电磁计算模型。计算电磁波在海水中的传播，分析低频电磁波在海水中的衰减规律，并通过与解析解对比，验证模型在计算海水中电磁波传播的正确性。进一步建立椭球形水下目标模型，基于三维海水色散介质FDTD 模型计算水下总场和散射电场分布，探究总场和散射电场随电磁波频率f的关系。讨论电磁波频率f和目标电导率σ对散射电场分布的影响，为实际水下探测提供参考。

1 三维色散介质中FDTD计算模型

针对建立三维海水色散介质计算模型，利用麦克斯韦旋度方程进行FDTD计算

式中：E、H、D 分别为海水中的电场强度，磁场强度和电位移矢量；μ为海水磁导率。电位移矢量D 和电场强度E在频域下满足

式中：ε0为真空介电常数；为复介电常数；ω 为角频率。海水为有耗散的色散介质，频域下在色散介质中与频率有关，

式中：σ为介质电导率；εr为相对介电常数。通过改变式（4）中εr以及σ 可得到某一频率下介质材料的复介电常数。将式（4）代入式（3）后得到频域下有耗散的色散介质中电位移矢量：

由于FDTD方法需要把时间差分，得到各时间点的电磁场，依照时间步求解电磁场瞬态变化。利用傅里叶积分变换可把式（5）变为关于时间t的积分，即

基于式（1）～（6），通过FDTD方法便可得到差分方程。结合划分的电磁场强度空间和时间三维差分网格，即可计算电磁场全空间全时段分布。图1 所示为海水深度x方向上电场和磁场在空间和时间坐标上的中心差分采样方法。三维色散介质的FDTD模型中，y和z方向的差分网格与x方向一致。

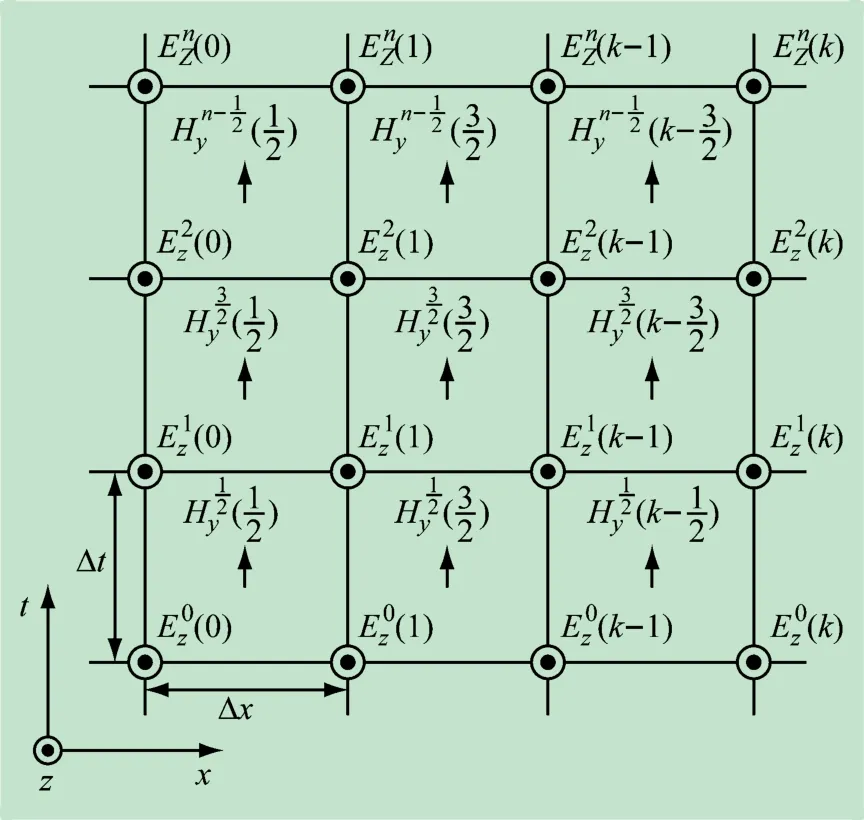
图1 计算区域海水深度x方向上空间和时间的中心差分网格

基于图1，以海水深度x方向为例，取时间离散间隔为Δt，空间离散间隔为Δx，将式（1）、（2）的电场强度E和磁场强度H在时间和空间上进行中心差分，得差分方程为

式中：上标n为计算的时间步长；k为计算的空间步长。

在差分中电场Ez在空间和时间的整数步长取值，磁场Hy在空间和时间的半整数步长取值。计算时间t＝n·Δt，n+1 为向前运行一个时间步，n+1／2 为向前运行半个时间步。在深度x方向计算的空间距离x＝k·Δx，k+1 为运行一个空间步，k+1／2 为运行半个空间步。

式（7）、（8）给出了E和H的差分关系，由于计算区域为海水色散介质，需对时域下的式（6）进行差分采样。将式（6）中积分近似为对时间步长Δt的求和，给出D和E的关系

从n＝0 时间步开始，引入正弦电场（k），结合式（9）电位移矢量的差分计算式，得（k）。代入式（7）、（8）便可依次求出（k+2）…，即可利用第k层空间步的电场值计算第k+1 层的值，从初始条件开始逐层计算。在n＝1 时间步，同样引入初始条件（k）和上一时间步的全空间电场强度代入式（7）、（8）便可依次求出（k+2）…。在时间上进行重复迭代便可得到计算区域内各个时间步的全空间水下电场分布。

为在计算区域边界处电磁波不发生反射，需在边界处引入完全匹配层（Perfect Matched Layer，PML）［12］。PML基本原理为在计算区域边界设置一种和计算区域介质完全匹配的介质层，使得电磁波进入PML后不会反射并且完全衰减。PML 和计算区域设置及具体参数如图2 所示。

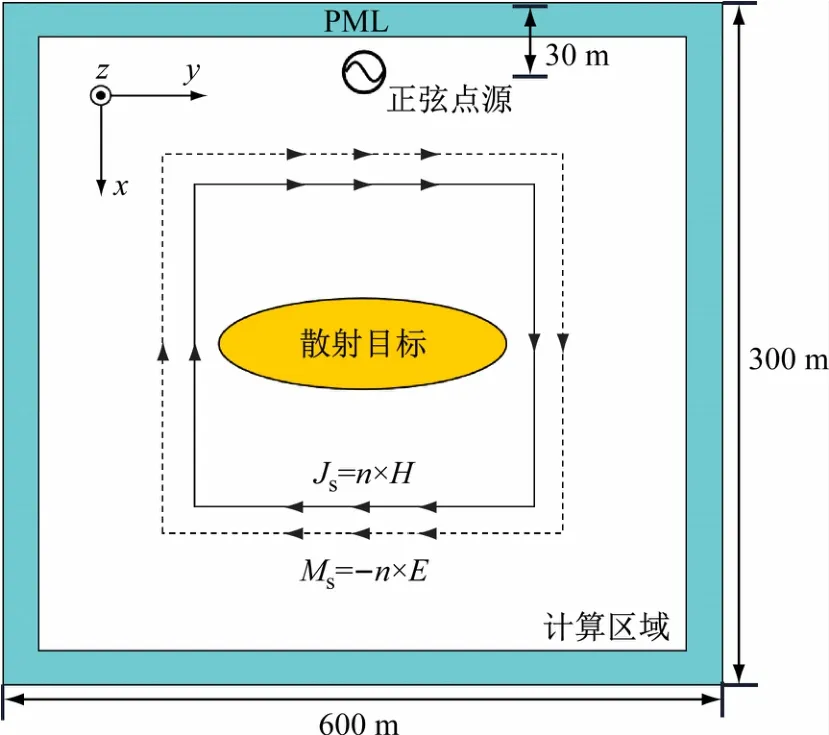
图2 吸收边界和计算区域示意图图中x为海水深度方向，y、z为海平面方向

计算过程中，电磁波由介质1 传播至介质2 时，电磁波的反射系数Γ 由两种介质的内在波阻抗决定。为使电磁波在PML 内不发生反射，需在PML 边界处应保持Γ不变。电磁波在两介质处反射系数

式中，η1、η2分别为介质1 和介质2 的波阻抗。波阻抗

式中：μ为介质的磁导率；εr为介质的相对介电常数。因此PML层设置磁导率和相对介电常数参数，需满足阻抗匹配条件［13］：

式中：n为法向；t为切向。

由于电磁波在PML内衰减，式（11）中的相对介电常数和相对磁导率须考虑损耗，即存在虚部

式中：σ（ρ）为PML内的电导率；ρ为到PML内边界的距离；σm为用导磁率表示的电导率；在阻抗匹配条件式（11）下与σ（ρ）等价。σ（ρ）通常写成幂指数形式：

式中：σmax＝；d为PML 的厚度；δ 为空间步长；m为常数。本文中将m设为4，确保PML 具有较好的吸收效果。

式（12）在计算中设为边界两侧的切向电磁参数相同

综合式（1）、（2）、（13）～（15）可得PML内麦克斯韦方程：

式（16）、（17）与计算区域内的麦克斯韦方程形式相同，因而可选用相同的迭代公式。

利用式（7）～（9）、（16）、（17），结合图1 划分的差分网格和图2 设置的吸收边界和计算区域便可计算得到全空间、全时段水下电磁场传播的总场与散射场。

2 水下电磁波传播散射结果分析

论文利用时域有限差分方法，构建了三维海水色散介质模型，计算水下目标电场强度的总场和散射场分布。设置参数：海水的电导率为σ ＝4 S／m，相对介电常数εr＝80，磁导率μ ＝4π×10-7N／A2［14］。划分的差分网格选取空间步长δ ＝1 cm，时间步长dt＝。其中，c0为真空中光速。在边界设置8 个空间步长间隔的PML模拟电磁波的吸收，确保图2 计算区域内电磁波无反射。

计算中采用正弦点源模拟水下电磁探测，将点源置于海平面下30 m处，点源差分

式中：f为正弦电磁波频率；t为运行的总时间步数。从初始条件正弦电场源开始逐步计算，在时间和空间上进行迭代得到全空间、全时段水下电磁场分布。

2.1 无散射目标FDTD数值解和解析解对比

为验证构建的三维海水色散介质中FDTD计算模型的正确性，计算无散射目标时水下电磁波传播和电场幅值衰减结果，并将FDTD 方法数值解与解析解进行对比。

在不考虑偏振的情况下，色散介质中电磁波所满足的传播方程可由式（1）、（2）解析求解：

式中：E0为发射源的初始幅度；α、β 分别为电磁波的衰减常数和相位常数；ηc为介质的本征阻抗。其中［15］：

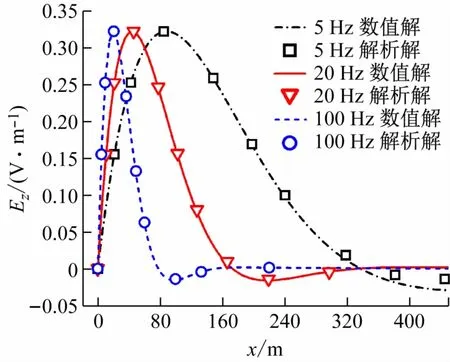
图3 不同频率水下电场强度Ez 在海水深度x方向上FDTD数值解与解析解对比

基于建立的三维色散介质模型，系统计算每个时刻下计算区域内的电场强度及其幅值。在图3、4 给出频率分别为5、20 和100 Hz的低频电磁波在海水中传播1.25 个周期时，电场强度及其幅值的FDTD数值解和式（19）的解析解对比。

由图3 可见，基于FDTD 方法得到电场强度数值解与解析解吻合很好，说明FDTD 方法计算数值结果的正确性和可靠性。进一步分析可得，随频率的降低，电磁波的波长越长，电磁波在海水色散介质中的衰减越弱，传播距离越远，有利于对海水中目标的探测。

由图3 可见，5 Hz电场强度FDTD 数值解与解析解在深度x＞300 m处有微弱偏差，误差极值为15.3 mV／m。该偏差的主要影响因素为电场的色散耗散误差kr，其与传播时间和划分的空间网格步长有关［16］。当频率很低时，电磁波在海水色散介质中的传播距离很长，传播时间也就长，造成色散耗散误差kr在深度x＞300 m处越大。

图4中给出了3 个频率下电场强度幅值数值解和解析解对比。由图中可见，随着频率f降低，电磁波的衰减变慢，传播深度增大。这是由于海水是色散介质，海水中自由电子在高频强电场的驱动下会在海水中形成电流密度，电场能量转变为焦耳热，造成电磁波在海水中传播的衰减。根据图4 中电场幅值变化曲线，可得海水中频率分别为5、20 和100 Hz 的电磁波，其电场强度幅值衰减到初始幅值的1／e时的传播距离分别为112.54、56.27 和25.16 m。对比图4 中各频率电场强度幅值衰减可见，电磁波在海水中的传播深度与式（21）中α 相关，即与为反比关系［17］。结合图3、4可得，当频率低于5 Hz 时差分计算有一定的幅值误差，会对FDTD模拟水下电磁探测产生影响。而当频率高于20 Hz时，电场幅值衰减过快不利于水下远距离探测。低频电磁波的幅值在海水中衰减较慢，且在探测区域中的电磁场显著大于洋流、潮波等海水运动切割地磁场产生的感应电磁场［18］，因此可用于水下目标的探测。超低频电磁波具有传播稳定、抗干扰能力强等优点，对水下大尺寸目标进行远距离电磁探测时应选用频率较低的电磁波，通过探测水下散射电场幅值分布探测水下目标的大小和位置。

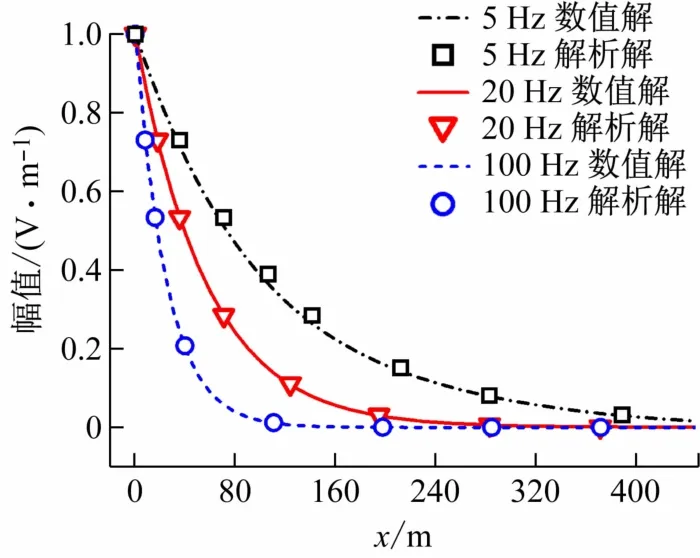
图4 不同频率水下电场幅值在海水深度x方向上FDTD数值解与解析解对比

2.2 计算水下大尺寸目标散射电场分布

实际探测中，水下目标如潜艇等呈流线型，将水下目标形状设为旋转椭球形，研究海水中椭球形目标散射电磁场的分布。旋转椭球目标长轴为120 m，短轴长为20 m，设置水下目标材料为钢铁，电导率σ ＝5 MS／m，相对介电常数εr＝8，相对磁导率μr＝1 000［19］。水下散射目标在计算区域位置如图2 所示，位于计算区域中心，椭球中心距离海面150 m，构建水下目标模型如图5 所示。

图5 水下椭球形目标模型

根据2.1 中分析，选择频率为10、20 Hz的正弦点源，构建好模型后利用FDTD方法进行差分，计算旋转椭球水下电磁场分布，并将x、y切面的电场强度幅值展示在图6 中。由于全空间电场分布具有较大的数量级差异，引入对数单位dB，其计算式为dB ＝20lg（A／A0），其中A为电场强度或幅值，A0＝1 V／m。

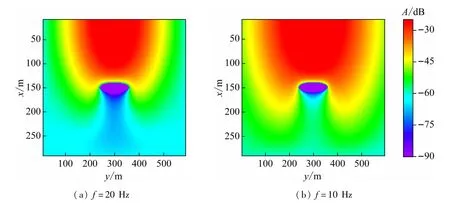
图6 不同入射电磁波频率水下目标的电场总场幅值分布

由图6（a）可知，由于金属目标散射的影响，不同深度的电场总场及散射场的幅值有显著差异。在深度30 ～100 m范围内即目标上方水下总场幅值呈e 指数规律衰减，目标散射电场的空间分布先增大后减小并趋近于0。其原因为水下目标产生的感应电场和散射电场在100 m处相互抵消，目标上方范围内散射电场起主导作用。在深度100 ～140 m 范围由于椭球目标的电导率较大，目标对水下电磁波的传播产生影响，散射电场迅速增大，与入射电场相互抵消，进而导致电场强度总场的幅值迅速衰减。在深度140 ～160 m范围，即水下目标内部，电磁波在目标表面位置被吸收，几乎无法传入目标内部，电场近似为0。这是由于入射到目标表面的电磁波发生了趋肤效应，电磁波在钢中无法传播，只能在其表面传播，在金属壳体表面产生了感应电流，进而在水下目标的下端产生散射电场，对电磁波传播起引导作用。当深度大于160 m即目标下方区域，由于目标对电磁波进行了阻挡，总场幅值逐步衰减，感应电流产生的散射电场起主导作用。散射电场随着深度的增加迅速减小逐渐趋近于0。由图6 可见，目标上侧散射电场比下侧强，其原因主要为低频场源离水下目标的上侧较近，电磁波目标对低频电磁波具有阻挡作用，散射电场主要分布于目标上侧。且水下目标的下端产生的散射电场来自于感应电流，其量级小于目标上侧。

由图6（a）可见，20 Hz电磁波在深度60 m处散射电场幅值为-48.41 dB，深度250 m 处电场幅值为-52.82 dB，当前水下电场探测量级可达μV／m，即-120 dB［20］，因此两处的散射电场均可被水下电磁探测器探测。将水下电磁探测器置于上述海水深度，将低频正弦点源置于图2 中所示位置在水下持续发射低频电磁波，通过分析有散射目标和无散射目标的电场总场幅值变化即散射电场便可精确确定目标位置。

根据图6（a）、（b）中不同入射频率下，水下电场幅值分布的对比可以发现，频率越高，在目标周围及其下方的电场总场幅值越大。在目标下方90 m 处即深度250 m处10 Hz入射源给出的总场幅值比20 Hz大-10.16 dB。说明10 Hz的电磁波相较于20 Hz探测距离更远，其水下电场的幅值变化更容易被电磁探测器精确探测。

2.3 入射电磁波频率对总场及散射场分布的影响

为研究入射电磁波频率对电场分布及水下电磁探测的影响，基于图5 水下椭球形目标模型和图2 设置的计算区域，选择频率为10、20 和30 Hz 的入射正弦点源，利用FDTD方法差分计算得到水下电场强度总场和散射场分布，结果分别展示在图7、8 中，分析不同频率电磁波的水下电磁探测效果。

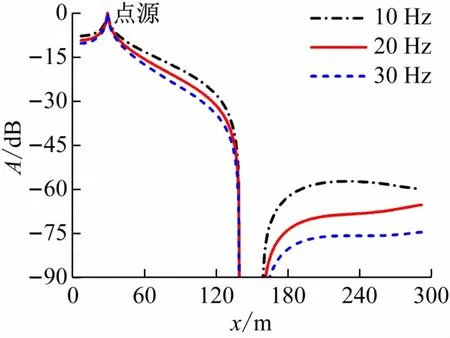
图7 不同入射电磁波频率在计算区域中轴线（y ＝300 m）处电场总场幅值分布

由图7 可见，总场幅值大小与入射正弦点源的频率有关，入射电磁波的频率越低，总场整体幅值越大。当探测电磁波频率高于30 Hz时，目标下方的总场幅值小于-80 dB。而海水洋流和潮波运动切割地磁场产生的感应电场数值大约在10-4量级，即为-80 dB左右［21］。海水运动产生的感应电场与30 Hz 入射电磁波的水下总场幅值数量级一致，海水背景运动以及背景磁场电场变化均会极大影响水下电磁探测［22］，在水下电磁探测中应选择频率低于30 Hz 的入射电磁波。由图7 可见，水下总场的整体幅值正比于e-■f，这可由电场强度和频率的关系式（19）解释。

图8 给出了不同频率电磁波水下散射电场在计算区域轴线上的分布。可见，随着深度的增加，散射电场幅值在目标上方范围呈先增大后减小的趋势。设旋转椭球体的高度为单位长度，在目标上方3 ～4 个单位长度处可达到散射电场的极值。在目标下方散射电场以e指数关系随深度迅速衰减至0。频率影响散射电场分布特征如下：①频率越低，海水中的整体散射电场幅值越大，越容易探测目标位置；②频率越低，目标上方散射电场的极值分布距离潜艇越远，表明可在更远处探测散射电场变化，探测更深处的潜艇位置。

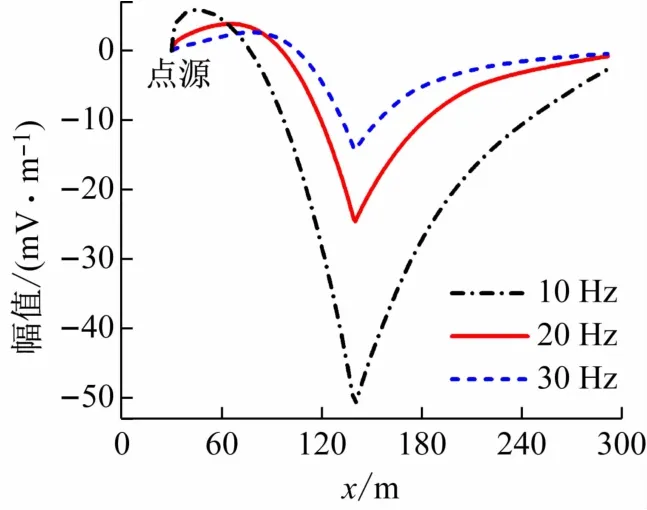
图8 不同入射电磁波频率在计算区域中轴线（y ＝300 m）处散射电场幅值分布

分析图7、8，频率影响总场和散射电场的原因主要有：①电磁波在水下的衰减与频率有关，频率低电磁波在水下的衰减弱；②金属表面产生的感应电流与频率相关，频率越低，感应电流越强，在目标上、下方产生的散射电场越强，散射电场的极值分布距离目标越远。例如将水下电磁探测器放置于目标上方95 m处，10 Hz入射频率的水下散射电场幅值为-44.65 dB，明显大于20 Hz的散射电场幅值。因此在水下电磁探测中应尽量选择频率低的入射电磁波。

综合以上可得，入射电磁波的频率越低，水下目标的总场和散射电场的整体幅值越大，散射电场极值分别距离潜艇越远，电磁探测效果越好。因此在水下探测时应选用频率较低的电磁波。

2.4 目标电导率对水下电场分布的影响

水下目标的电场分布不仅与入射电磁波的频率有关，还与目标的电导率有关。为探究目标电导率对水下电场分布的影响，利用FDTD 方法计算入射电磁波频率为20 Hz时，水下目标电导率σ分别为102、103和105S／m时的散射电场分布，并将结果展示在图9中。

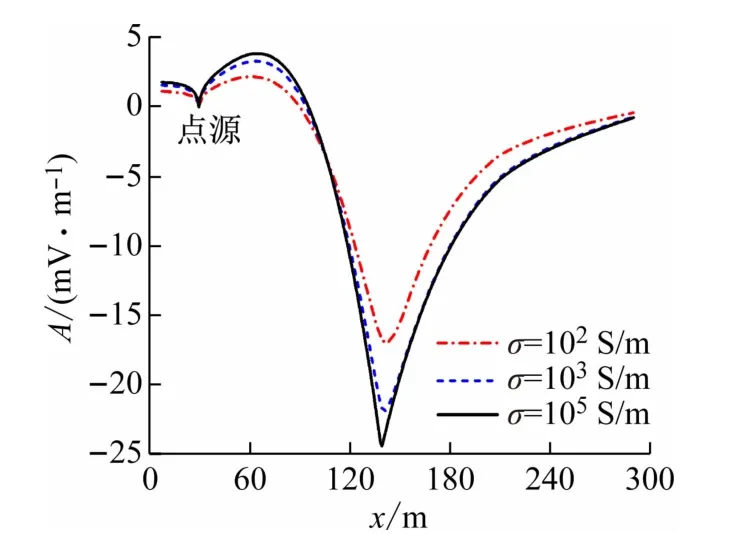
图9 不同电导率水下目标在计算区域中轴线（y ＝300 m）处散射电场幅值分布

图9给出了在计算区域中轴线（y＝300 m）处不同电导率水下目标的散射电场分布。可见，随目标的电导率增加，散射电场的整体幅值也增加，而散射电场的极值分布点保持不变，即目标电导率的变化仅影响散射电场幅值大小而不影响散射电场的分布。这从式（19）～（21）可知，目标电导率仅与电场幅值大小有关。目标材料的电导率越低，对电磁波的吸收也就越弱，表面感应电流产生的散射电场也就越小。

图10 给出了20 Hz入射电磁波频率下，不同电导率的水下目标在其上方75 m（散射电场极值）处散射电场FDTD计算幅值及其对数拟合曲线。可知，该处散射电场幅值在电导率0 ～2 000 S／m 区间内增幅明显，随电导率呈对数增加趋势。对该散射电场极值处的幅值和电导率进行拟合，即

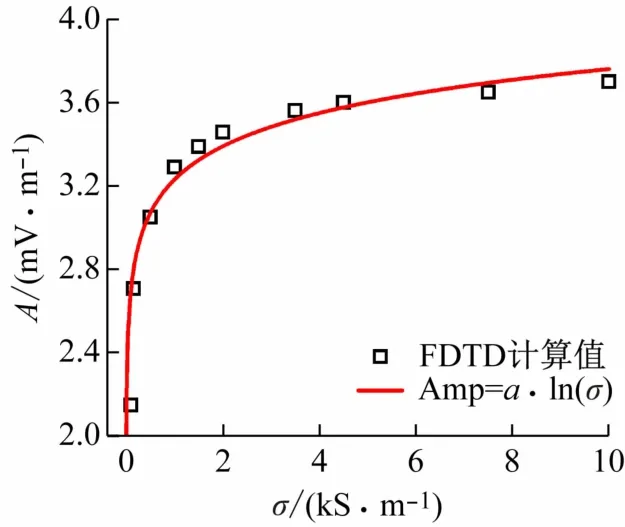
图10 20 Hz入射电磁波频率下不同电导率的水下目标在目标上方75 m（散射电场极值位置）处散射电场幅值FDTD计算结果及对数拟合曲线

得到拟合曲线中的参数分别为：a＝0.231 mV／m、b＝1.21 kS／m。图10 给出了对数拟合结果和散射电场幅值FDTD计算结果吻合得很好，说明散射电场极值处的幅值正比于ln σ。图中，当目标电导率大于2 kS／m后，散射电场幅值的增幅逐渐变小直至趋于稳定，这是由于当目标电导率很大时，根据趋肤效应，电磁波已无法传入金属内部，各种电导率的水下目标对电磁波传播的影响一致，在目标表面产生的感应电流基本相同，感应电流产生的散射电场变化趋于稳定，导致不同电导率下水下目标的散射电场趋于稳定。

当前水下目标外壳材料更新较快，在选用高强度钢满足下潜承受力的同时还会选择添加复合材料用于耐海水腐蚀和增强电磁信号的传播［23］。这会导致目标的电导率降低，也就难利用电磁波精确探测到目标的位置。假设水下电磁探测的极限为5 mV／m，则该电磁探测器将无法精确探测电导率小于105S／m的水下目标。结合图9、10 可见，水下目标的电导率越大，散射电场在水下的整体幅值越大，也就越容易被电磁探测器精确探测。当电导率大于2 kS／m后，增幅变化逐渐趋于稳定，即电导率的变化不会影响目标散射电场的探测。

3 结语

在海水色散介质中，建立三维时域有限差分电磁计算模型。结合构建水下椭球形散射目标，计算全空间不同时刻下水下目标的电场强度总场和散射场幅值分布，得到水下不同深度处总场和散射电场的变化规律。通过对结果分析发现，入射电磁波频率和目标电导率对水下探测有直接影响。对于频率f，水下总场和散射电场的整体幅值正比于，且频率越低，散射电场极值位置距离目标越远，电磁探测效果越好。对于目标电导率σ，散射电场幅值在目标电导率0 ～2 000 S／m区间内增幅明显，后变化趋于稳定，散射电场极值正比于ln σ。本文的研究结果，分析并解释了频率和目标电导率对水下目标散射电场的影响，可为后续水下电磁探测应用提供理论参考。