风力发电用锂离子电池均衡控制

师振贵， 施佳锋， 彭嘉宁， 马冬冬， 张 倩， 王 斌

（1.长江大学地球科学学院，武汉 430100；2.国网宁夏电力有限公司，银川 750001；3.湖北工业大学电气与电子工程学院，武汉 430068）

0 引言

风力发电因其清洁、可再生被广泛应用，但其发电功率受环境因素影响非常大，故大部分会使用锂离子电池储能系统来平抑其功率输出［1］。由于生产以及制造存在差异，大量锂离子电池串并联使用后其一致性会变差［2］，故需对电池组进行均衡，最大化利用电池组可用容量［3］。

目前判断电池组是否均衡的指标主要是电池端电压、电池荷电状态（state of charge，SOC）以及电池剩余容量［4-6］。电池均衡的目的是实现电池同时充满以及同时放空，最理想的指标是电池剩余容量，其次是电池SOC，最后才是电池电压［7-8］。对于风力发电储能系统来说，使用电池剩余容量或电池SOC为指标是不切实际的，对于整个储能系统，估算电池组中所有单体电池的剩余容量或SOC是几乎不可能的［9］，电池SOC估算本就是目前锂离子电池技术的研究热点与难点，准确估算锂离子电池SOC非常困难［10-11］，更何况估算所有电池的SOC，再者，估算所有电池剩余容量难度比估算电池SOC更大，所以上述两种方法并不适用于风力发电储能系统［12］。采集电池的电压是非常简单的，有非常多的解决方案，单体电池端电压是电池管理系统（battery management system，BMS）在运行过程中必须时刻关注的变量［13］，它关系到电池组是否过充、过放，电池端电压可以较好地反应电池剩余容量，故目前风力发电储能系统基本都使用电池端电压作为判断是否均衡的指标［14］。

电池端电压仅仅只能部分反映电池剩余容量，在实际应用过程中依旧存在很大的不足，很容易使得BMS出现误判。目前的研究主要集中于在电池端电压基础上增加电阻，容量等参数，以弥补其不足，这些方法很容易在简便性与性能方面顾此失彼［15-17］。

本文提出一种新的均衡控制策略，在技术方面依旧使用电池端电压作为均衡指标，通过对指标进行转换，弥补其在均衡结束时刻易误判的不足，以改善以电压为指标的控制策略不足。

1 通用策略分析

1.1 原理分析

假设电池组由2 节电池串联组成，记最高电压电池为A，其电压为UA，最低电压电池为B，其电压为UB。如果它们的电压之差满足

则BMS启动均衡。式中，Uo为均衡启动压差。启动均衡后，均衡系统为电池B 充电或为电池A 放电，实现电池均衡目标，此处以均衡系统为电池B 充电为例，其剩余容量缓慢增加，对应的其电压也缓慢上升，当上述两个电池的电压满足

均衡结束。式中，Uc为均衡结束压差。

图1 所示为通用策略流程，由图1 可知，通用策略只需要电池端电压即可，其控制简单，且可靠，故被广泛应用于风力发电储能系统等场合。

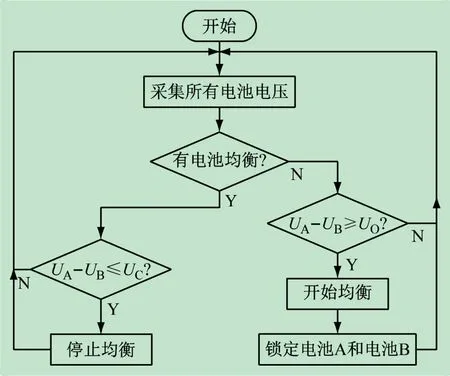
图1 通用策略流程

1.2 不足分析

通常，电池开路电压Uoc与电池SOC 存在函数关系

图2 为电池等效电路，图中：U为电池端电压；I为电池电流；g（I，t）为电池极化电压；Cp为电池极化电容；Rp为电池极化电阻；t为BMS 运行时间；h（I，R）为电池的欧姆电压；R为电池欧姆内阻。由图可知，电池端电压U与f（SOC）的关系

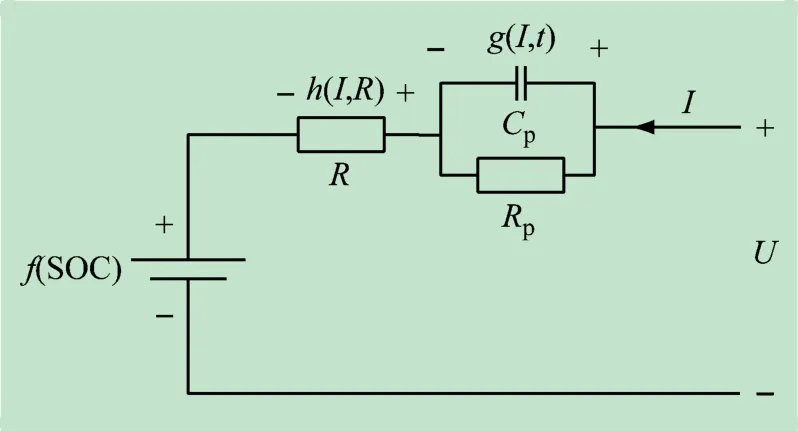
图2 电池等效电路

最高电池电压

式中：f（SOCA）为最高电压电池UOCA；SOCA为最高电压电池SOC；g（IA，t）为最高电压电池极化电压；h（IA，RA）为最高电压电池的欧姆电压；IA为最高电压电池的电流；RA为最高电压电池的欧姆内阻。

最低电池电压

式中：f（SOCB）为最低电压电池UOCA，SOCB为最低电压电池SOC；g（IB，t）为最低电压电池极化电压；h（IB，RB）为最低电压电池的欧姆电压；IB为最低电压电池的电流；RB为最低电压电池的欧姆内阻。

通常，当BMS启动均衡后，系统会实时刷新上述两节电池的电压差，当UA＝UB时，BMS 会停止均衡。由于BMS实现电池均衡的手段是控制每节电池充、放电电流，故可得：

这会导致在UA＝UB的前提下，SOCA≠SOCB，即BMS并没有实现既定的电池均衡目标，并且，如果电池间均衡电流越大，其差异也越大。

2 本文提出的策略

2.1 原理分析

当电池组未均衡时，串联电池组中所有电池电流是一样的，即IA＝IB，同时，电池在出厂时可以认为其参数是一致的，即每节电池的极化电压函数g（I，t），欧姆电压h（I，R）可以认为是一致的，此时，在电池组均衡开始前，UA与UB的关系：

也就是说，此时电池间端电压之差就可以视为是电池OCV之差。需要强调的是，电池在生产以及使用过程中确实存在些许不一致，该不一致经过很多次充、放电循环后会被放大，反映到电池组上就是剩余可用容量不一致，但是这些不一致其实是非常小的，对于实际应用，可以忽略。

在不同SOC 区间，使用多个分段线性函数表示f（SOC）时，其函数关系为

式中：k、b为拟合参数；i为不同区间标号。在相同SOC区间内

f（SOCA）与f（SOCB）之差

UA与UB之差

也就是说，电池端电压之差与其SOC 之差存在特定的线性关系，即可在均衡开始前，根据电池端电压之差计算它们的SOC之差。

由上述分析中可知，此结论成立的前提是需要最高SOC电池以及最低SOC 电池处于相同SOC 范围，在实际使用中，BMS 只会实时估算电池组SOC，即电池组平均SOCa，其满足下式：

式中，SOCH、SOCL以及SOCd分别为电池组中最高电池SOC、最低电池SOC 以及电池组SOC 的最大偏移值。

由于均衡系统的存在，电池组中所有电池的SOC都会被均衡至相对均衡状态，故当电池组SOC满足

可以认为电池组中所有电池SOC 都在相同SOC区间内。当获得电池组间SOC 之差ΔSOC 时，由于在均衡过程中，电池组间电流差异仅为均衡电流，即当均衡时间T满足下式：

图3所示为所提控制策略流程，由图3 可知，所提策略相较于通用策略，在流程上仅仅只有3 处做了改变（图3 中标黄处），在判断电池均衡前增加了电池组SOC区间判断，而判断电池组是否开启均衡的条件与通用策略一样，只不过在均衡开始前会计算ΔSOC，然后利用式（18）来确定是否结束均衡，以此来规避通用均衡策略用电池端电压带来的弊端。

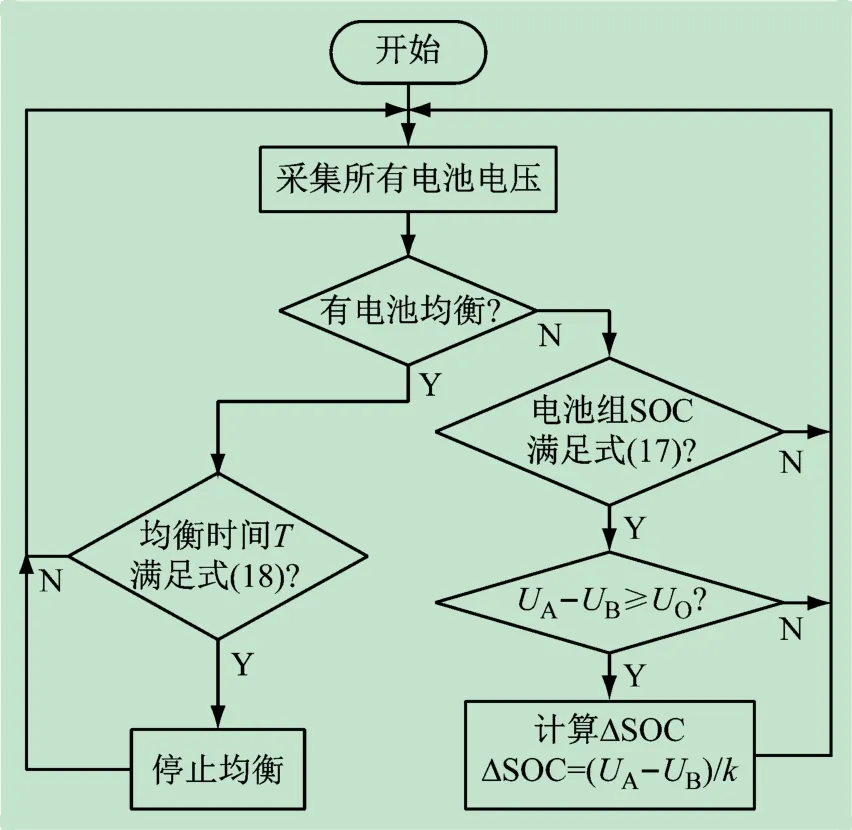
图3 提出的控制策略流程

2.2 适用性分析

对于风力发电用电池均衡系统，估算每节电池SOC或剩余容量，以此为指标实现电池均衡是不切实际的，电池端电压可很容易获取，对于风力发电以电池端电压为指标会被广泛应用。

由上述分析中可见，所提策略相较于通用均衡策略，增加了OCV-SOC 关系中k值计算以及式（18）中对均衡结束时间的判断。对于电池SOC 估算，OCVSOC关系的获得是必须的，所以本文所提出的策略仅仅只需要从已获得的数据中计算相应k值即可。式（18）的计算对于目前主流芯片，实现方式极为简单，计算量可以忽略不计，所提策略在技术上是可行的，且几乎跟通用策略一样简单。

在效果上，本文所提策略使用SOC 为指标，它不会受到电池均衡电流的影响，即便BMS 关闭均衡后，均衡电流消失也不会影响其状态，而通用策略使用的是电池端电压，该指标容易受到电池均衡电流的影响，在有均衡电流（均衡阶段）以及无均衡电流（未均衡阶段）条件下，相同剩余容量的电池其端电压会明显不一样，这样就使得BMS出现误判。故本文所提策略可以较好地规避通用策略的不足。

3 实验结果分析

3.1 实验平台

本文使用4 串标称电压为3.9 V钴酸锂聚合物电池进行测试，电压采样芯片使用LTC6803，均衡电流检测芯片使用ACS712-05。

图4 所示为使用的均衡电路，由图4 可知，每节电池使用两个开关控制均衡电源为最低容量电池进行充电，当电池B1需要被均衡时，打开Q1、Q2，让均衡电源为电池B1充电即可。均衡电源使用电源模块，该模块输出电压为5 V。

图4 使用的均衡电路

3.2 测试分析

图5所示为通用策略实验结果，由图可知，开始B1被均衡，约到第40 s，B1、B2的电压之差为0，满足关闭均衡的条件，此时BMS 关闭均衡。需要注意的是，由于B1没有均衡电流，其电压出现较大幅度的下落，虽然它的端电压出现较大变化，但此时它的SOC并没有变化，也就是说，关闭均衡时BMS 以它们端电压一样认为两节电池SOC 也一致，但事实上B1的SOC依旧低于B2的SOC，B1并没有被充分均衡。

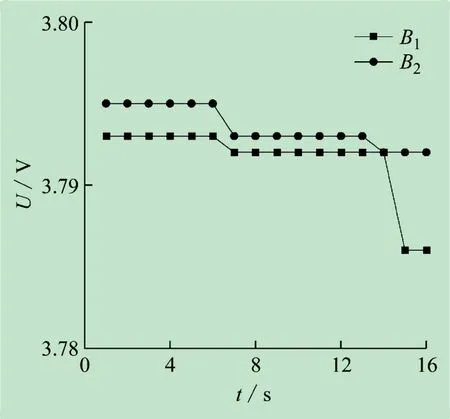
图5 通用策略实验结果

图6为拟合的SOC-OCV 曲线，由图可知，本文将电池SOC划分为4 个区间，获取4 个区间不同的k值，SOC与OCV的关系为：

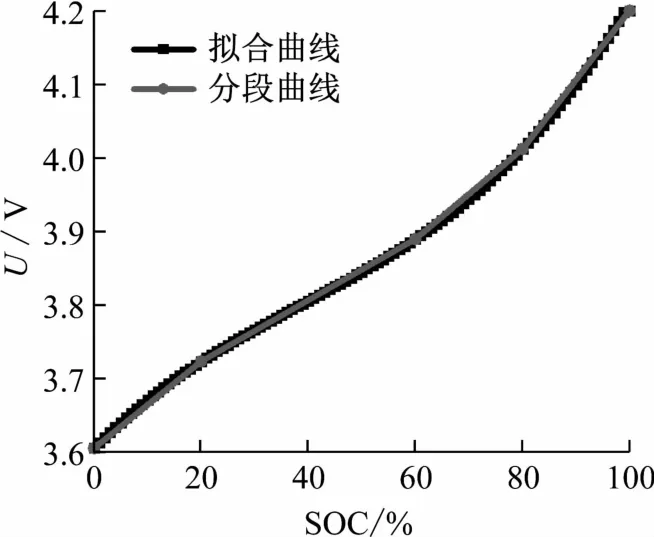
图6 拟合的SOC-OCV曲线

取SOCd＝3%，则

根据电池组SOC所在区间，就可确定电池端电压之差与电池SOC之差的系数。

图7 为电池放电实验结果，根据电池组SOC 可知k值为9.4，由于B1、B3的端电压之差约为8 mV，所以换算成SOC之差约为0.85%，BMS 开启均衡后，将不再以电池端电压来判断电池是否需要结束均衡，而是以对均衡电流积分的时间来确定，约到370 s，BMS 计算的均衡电流积分等于SOC之差后，关闭均衡，B1、B3之间的电压差约为1 mV，较好地实现了电池均衡的目标。图中，虽然B1的端电压在约第100 s超过了B3，但BMS并没有停止均衡，此时B1并未被充分均衡，本文所提策略在通用策略的基础上，BMS 将均衡延长约270 s以抵消均衡电流对B1端电压的影响。

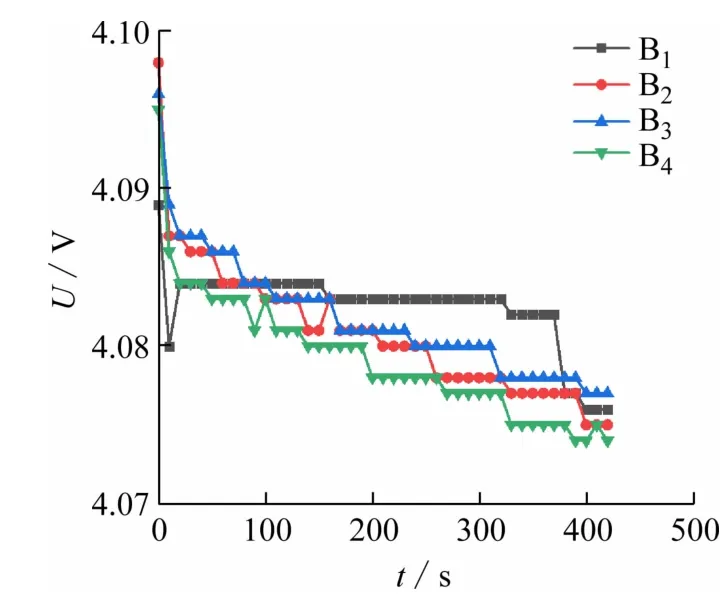
图7 电池放电实验结果

图8为电池静置实验结果。根据电池组SOC 可知k值为6.15，B1、B3的SOC之差约为0.98%。虽然B1端电压在约50 s已高于B3，但由于BMS 并未以电池端电压为基准判断，故BMS 并没有关闭均衡，直至约400 s，对均衡电流进行积分获得的SOC 变化达到电池均衡前的SOC差异，故此时结束均衡，最终B1、B3的端电压之差约1 mV。

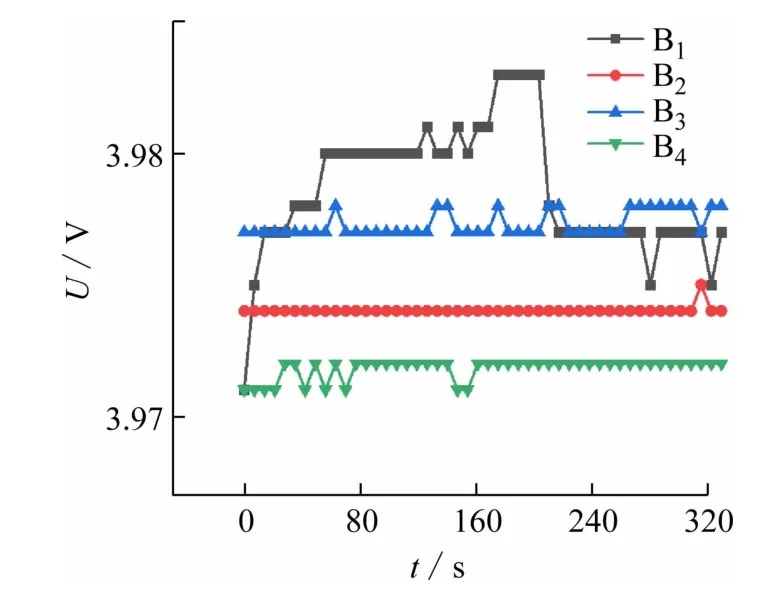
图8 电池静置实验结果

图9为电池充电实验结果，此时k值为4.1，计算出B2、B4的端电压之差为5 mV，估算出BMS 需要在均衡开启后，对均衡电流积分至其SOC 变化为1.2%即可，约到第480 s，均衡完毕，B2的电压出现较大回落，略低于目标B4的电压，但最终也较好地实现了电池均衡的目标。

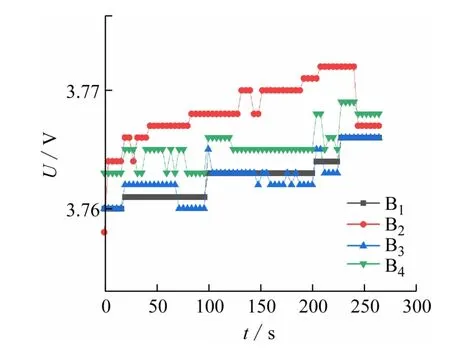
图9 电池充电实验结果

相较于图5，本文所提策略在电池组充电、放电以及静置阶段都可取得较好的均衡效果，且该方法易于实施，对目前风力发电用锂离子电池均衡控制策略来说具有较好的替代性。

4 结语

本文提出了一种适用于风力发电用锂离子电池均衡控制策略，并且设计实验进行测试，结果表明，将电池SOC划分为多个区间后，计算电池SOC 之差，以电池SOC之差为指标比以端电压为指标有更好的均衡效果。