Scale-up and thermal stability analysis of fluidized bed reactors for ethylene polymerization

Xiaoqiang Fan ,Jingyuan Sun,Jingdai Wang ,Zhengliang Huang ,Zuwei Liao ,Guodong Han ,Yongrong Yang

1 Ningbo Research Institute, Zhejiang University, Ningbo 315100, China

2 State Key Laboratory of Chemical Engineering, College of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, China

3 Zhejiang Provincial Key Laboratory of Advanced Chemical Engineering Manufacture Technology, Hangzhou 310027, China

4 Sinopec Tianjin Company, Tianjin 300271, China

ABSTRACT A set of hydrodynamic similarity laws is applied to the scale-up of ethylene polymerization fluidized bed reactors(FBRs)under the condensed mode operation.The thermal stability of open-loop controlled FBRs is investigated by the homotopy continuation method.And the Hopf bifurcation point is selected as an index of the thermal stability similarity.The simulation results show the similarity in state variables,operation parameters,the space–time yield(STY),and the thermal stability of FBRs with different scales.Furthermore,the thermal stability behaviors and similarity of the closed-loop controlled FBRs with different scales are analyzed.The observed similar trend of Hopf bifurcation curves reveals the similarity in the thermal stability of closed-loop controlled FBRs with different scaling ratios.In general,the results of the thermal stability similarity confirm that the hydrodynamics scaling laws proposed in the work are applicable to the scale-up of FBRs under the condensed mode operation.

1.Introduction

Polyethylene (PE) is one of the five general synthetic resins.According to density,it can be classified as high-density polyethylene (HDPE),Medium-density polyethylene (MDPE),low-density polyethylene (LDPE)/ linear low-density polyethylene (LLDPE),etc.Among all the ethylene polymerization processes,the gasphase polymerization process is used to produce nearly all types of polyethylene,from HDPE to VLDPE.The gas-phase polymerization processes are usually very short,simple for operation,and easier for product devolatilization [1].Thus,the gas-phase polymerization processes are widely applied to ethylene polymerization around the world.

In order to improve the capacity of gas-phase fluidized bed reactors(FBRs),the condensed mode operation is developed based on the conventional gas-phase polymerization process.In the condensed mode,the inert condensed medium and comonomer with a relatively higher boiling point temperature are added into the recycle stream [2,3].Then the recycle stream can become a gas–liquid mixture under a reasonable temperature.Thus,the heat removal ability of the recycle stream and the production rate will dramatically increase [4,5].The condensed medium also significantly affects the solubilities and the diffusion behaviors of vapors in polyethylene [6,7].Generally,the liquid fraction of the recycle stream is below 20%(mass)so as to keep a stable operation of fluidized beds,therefore the space–time yield(STY)of FBRs under the condensed mode operation is usually 1–2 times larger than that of FBRs under the gas-phase mode operation.There are dispersed liquid droplets,wet and dry solid particles and continuous gas coexist in the fluidized bed reactor.Therefore,researchers and engineers should take into account both the hydrodynamic scaling laws and the polymerization reactions characteristics and the liquid evaporation in the scale-up processes of ethylene polymerization fluidized bed under the condensed mode operation.

The hydrodynamic scaling laws of FBRs have been wildly investigated by dimensionless analysis.With the dimensionless parameters being equal at all scales,hydrodynamic similarity will be ensured.Glicksman [8] proposed a full set of scaling laws by non-dimensionalizing the equations of motion and conservation of mass of the gas and particle phase and the Ergun equation.However,the full set of scaling laws can hardly be fulfilled.In order to reduce the fixed parameters,Glicksmanet al.[9] developed asimplified set of scaling laws by simplifying the Ergun equation for situations where the fluid-particle drag force is either dominated by viscous forces or dominated by inertial forces.Horioet al.[10]derived the phenomenological model of bubbling beds on potential theory and proposed a set of scaling laws related to the superficial gas velocity,the initial fluidized gas velocity,and the fluidized bed diameter.Schoutenet al.[11] suggested an empiric dimensionless entropy group that the Kolmogorov entropy must be kept constant for the scaling up of FBRs.The proposed scaling laws are related to the fluidized bed conditions,the particle properties,and the fluidized bed diameter.However,the use of empirical correlations to obtain the dimensionless entropy group limits its practical application.

For chemical reactors,a scale change will always influence the conversion and selectivity which depend on the interactions of mass transfer,heat transfer,reaction kinetics and hydrodynamics[10,12].Therefore,the chemical similarity and the hydrodynamic similarity must be considered simultaneously.For the scaling up of an ethylene polymerization reactor,the chemical similarity in terms of conversion and selectivity is hardly applied as the conversion of ethylene is usually very low and has no byproduct.Thermal stability is a common problem for chemical processes and is of significance for ethylene polymerization process safety and production quality.From some experiments and industrial data,it has been reported significant fluctuations in reaction parameters such as reactor temperature and pressure[13,14].Therefore a simplified set of scaling laws in terms of thermal stability (i.e.Hopf bifurcation) is proposed here.The thermal stability problem of the ethylene polymerization process can be divided into three subproblems: particle scale thermal stability [15,16],plant scale thermal stability [17–19],and polymerization system stability[20,21].Here we focus on the plant scale and the open-loop stability of the fluidized bed reactor.

The thermal stability of ethylene polymerization FBRs is controlled by polymerization kinetic parameters,particle properties including the particle diameter and the particle structure,mass transfer and heat transfer behaviors including internal diffusion and external diffusion,and operation parameters,such as superficial gas velocity,liquid feed rate,catalyst feed rate,etc.Effects of the above-listed control factors on the thermal stability,bifurcation characteristics,and dynamic behaviors of ethylene polymerization FBRs have been widely investigated in previous studies.Choi and Ray [22] proposed a simplified two-phase model for gas-phase polyethylene fluidized bed reactors.And the Routh-Hurwitz method was applied to obtain the criteria for static bifurcation points and Hopf bifurcation points (HBPs) of the gas-phase ethylene polymerization process and propylene polymerization process.Ghasem[23,24]studied the effects of particle size,particle growth rate and particle internal diffusion coefficient on the thermal stability of a gas–solid fluidized bed polymerization reactor.It was found that both the particle size and diffusion coefficient of reactants had significant effects on the thermal stability of the reactor.Salauet al.[25] investigated the stability and dynamic behaviors of a gas-phase polyethylene fluidized bed reactor,and pointed out that the safe operation range is very narrow for gasphase polyethylene reactors without a reactor temperature feedback controller.Luoet al.[18]proposed a gas-phase horizontal agitated fluidized bed model for the propylene polymerization reactor,and studied the stability and dynamic behavior of gasphase reactors with/without a reactor temperature feedback controller.However,there are few studies on the influences of the reactor size scale on the thermal stability of FBRs,especially for polyethylene FBRs under the condensed operation mode.

In this paper,the thermal stability similarity of different scale polyethylene FBRs under the condensed operation mode is the main topic.Therefore,the reactor diameter is selected for the investigation of the stability behaviors of FBRs under the condensed mode operation.The fluidized bed reactor operated under the condensed mode is quite different from the slurry reactor[26–28].As the condensed mediums usually have a relatively high boiling point,the injected liquid can’t immediately evaporate.Then the injected liquid is in the form of dispersed droplets or film on particles in the fluidized bed reactor.An evaporation model is applied referring to the previous work[29–31].In order to investigate the thermal stability similarity between reactors with different bed diameters,the steady states of the FBR are calculated by the homotopy continuation method [32],and the bifurcation points are detected by bifurcation theory [33].Hopf bifurcation is a relatively simple and important dynamic bifurcation problem.When the system parameters change through the critical value(Hopf bifurcation point),the equilibrium point becomes unstable and the limit cycle appears.In our previous work[31,34],the Hopf bifurcation is also observed.Therefore,the Hopf bifurcation points are selected to analyze the thermal stability similarity in the present work.More specially,the state variables,operations and space–time yield at Hopf bifurcation points of FBRs with different scales were compared.

2.Mathematic Model

2.1.Model assumptions

Based on the classical two-phase model [35–37],a multizone model is proposed to describe ethylene polymerization in a fluidized bed operated under the condensed mode.As shown in Fig.1,the fluidized bed is composed of the emulsion phase and the bubble phase,and the emulsion phase both of which are divided into a gas–liquid-solid (G-L-S) zone and a gas–solid (G-S)zone in the multizone model.

Assumptions for the multizone model are as follows.

(1)The fluidized bed is a dense fluidized bed,and both the G-L-S zone and G-S zone are divided into an emulsion phase and a bubble phase.

(2)Both the solid particle,the liquid phase and the gas phase in the emulsion phase are well mixed,and the voidage of the emulsion phase is equal to the bed voidage at the minimum fluidizing condition.

(3) Gas passes through the bubble phase as plug flow.

(4) The condensed liquid is injected into the emulsion phase of the G-L-S zone and hence spread on solid particles.

(5) The condensed liquid evaporates and transfers into emulsion gas directly.

(6)The temperature of solid particles,condensed liquid and gas in the emulsion are equal,and heat absorbed by liquid evaporation completely comes from the emulsion phase.

(7) The activation time of the catalyst is neglected.

(8) The hydrodynamic parameters such as the minimum gas velocity are uniform through FBRs.

2.2.Mass balance equations

The mass balance equations of ethylene and 1-hexene in the emulsion phase of the G-L-S zone are described by Eqs.(1)and (2),respectively.On the right side of Eq.(2),the terms stand for the variation of 1-hexene concentration related to the convection,mass transfer between bubble phase and emulsion phase,1-hexene consumption by polymerization,1-hexene entrainment by the product discharge,and 1-hexene converted from liquid phase sequentially.The subscript ‘‘1” and ‘‘2” in the variable symbols of concentration and temperature stand for the G-L-S zone and G-S zone,respectively.

Fig.1. Schematic diagram of liquid containing fluidized bed reactor.

The mass balance of nitrogen in the emulsion phase of the G-L-S zone is described by Eq.(3).

In this work,the solubilities of ethylene,hydrogen,and nitrogen in the condensed liquid are neglected.The mass balance of the condensed liquid (or 1-hexene in the liquid state) is expressed as Eq.(4).

The volume fraction of the G-L-S zone is determined by the accumulated condensed liquid in the fluidized bed.It is expressed as

WhereaDis the specific surface area of solid particles,and δlis the thickness of the liquid film.The liquid film thickness is determined according to our previous work [31].

The mass balance of ethylene and 1-hexene in the emulsion phase of the G-S zone is described by Eqs.(6) and (7).

The mass balance of nitrogen in the emulsion phase of the G-S zone is described by

The mass balance of the concentration of componentiof zonejin the bubble phase is given by

The quasi-steady-state equation is solved and the averaged values of the concentration of componentiin zonejare given by

The first order deactivation kinetic model is employed and the mass balance of the catalyst is expressed by Eq.(11)

Where the volume of product withdrawn from the fluidized bed reactorQeis equal to the production rate given by

Compared with the initiation of active sites and chain transfer reaction,the chain propagation reaction is the main consumption of ethylene and 1-hexene.Therefore,only the chain propagation reaction is considered in this work [20–22].The propagation rate constant follows the Arrhenius laws,

2.3.Energy balance equations

The energy balance of the emulsion phase of the G-L-S zone is given by Eq.(14).On the right side of Eq.(14),the terms represent enthalpy variation of the emulsion phase related to ethylene concentration gradient,inlet and outlet flow temperature gradient,heat transfer between bubble phase and emulsion phase,polymerization reaction heat,heat removed by solid and entrained gas,heat removed by condensed liquid evaporation,and heat exchanged between the G-L-S zone and G-S zone,respectively.

Similarly,the energy balance of the emulsion phase in the G-S zone is given by Eq.(15).

Neglecting the concentration change ofCiin the bubble phase,the energy balance of the bubble phase in zonejcan be expressed as Eq.(16).

2.4.Evaporation model

In this work,the injected liquid is well mixed and forms liquid film with a certain thickness on the surface of solid particles.Then liquid evaporation in the G-L-S zone can be treated as liquid film evaporation on particles.Because the liquid evaporation rate obeys the equilibrium evaporation principles [29,38],thus evaporation rate is related to the concentration gradient between the saturated vapor and the bubble phase.More information on the evaporation model can be found in our previous work [31].

2.5.Model parameters and solution method

The hydrodynamic parameters,namely,the minimum fluidization velocity,the bubble velocity,the bubble fraction,the minimum voidage,the bubble diameter,the solid circulation rate,the mass and heat transfer coefficient between the bubble phase and the emulsion phase are estimated through theoretical and semiempirical correlations according to our previous work.Physical constants and parameters listed in Table 1 are estimated based on a commercial fluidized bed reactor with an annual production capacity of 120000 t LLDPE.

Combining mass balance equations,energy balance equations and evaporation equations,the detailed model of liquid containing fluidized bed reactor is established.The calculation of the steady states and the detection of Hopf bifurcation points are carried out through MATCONT [39] software.

3.Results and Discussion

For the scale-up of fluidized bed reactors,keeping a stable steady state in terms of thermal stability is as important as keeping the hydrodynamic similarity.In fact,the thermal stability and the hydrodynamic stability are inter-coupling.On one hand,the hydrodynamics behaviors such as relative velocity between particles and gas,voidage of the dense phase and the dilute phase(that is bubble phase in the bubbling fluidized bed),and the bubble velocity have significant impacts on the heat transfer coefficient and the mass transfer coefficient between the gas-phase and the solid phase.Therefore,keeping similar hydrodynamic behaviors of FBRs helps to ensure a similar reaction environment and the same thermal stability in the scale-up process of FBRs.On the other hand,the similar stable state of reaction conditions in terms of the thermal stability of FBRs helps avoid temperature oscillation,particle aggregation and melting,or liquid accumulation in the fluidized bed.In fact,particle aggregation and liquid accumulation in the fluidized bed may result in significantly different hydrodynamics.The hydrodynamics behaviors of FBRs are on the mesoscopic scale,because they are related to particles,clusters,and bubbles,while the thermal stability is on a macroscopic scale.The thermal stability of FBRs not only has tight interaction with the hydrodynamic behaviors but also considers mass and heat transfer behaviors.The thermal stability in the scaling up of FBRs is the main topic here.

To eliminate the influences of hydrodynamic behaviors on thermal stability,a set of simplified hydrodynamic scaling laws are directly proposed here based on Glicksman scaling laws [8,9].

For ethylene polymerization,it is necessary to keep the same particle diameter for FBRs with different bed diameters.For one thing,the catalyst should stay in the fluidized bed with an optimal residence time.The catalyst content or catalyst diameter is applicable to adjust PE particle diameter.However,as shown in Eq.(17),the local Reynolds number will change due to the variation of particle diameter,while the density and viscosity of the gas phase are usually kept constant.Therefore,the hydrodynamic similarity is hard to be guaranteed.For another thing,in the scale-up process,changing particle diameter means a redesign of the downstream equipment,such as the discharge system,the purge bin,the extruding equipment,etc.In conclusion,keeping the particle diameter constant in the scale-up of FBRs not only ensures similar hydrodynamic behaviors but also helps reduce time and expense for the design of new plants.According to the hydrodynamics scaling laws,the physics parameters consisting of the gas density,the gas viscosity,etc.should remain the same for different scale FBRs.Although both the gas density and the gas viscosity are affected by reactor temperature,pressure,and mediums in the gas,the gas physics parameters have little variations under certain operating conditions.At last,the ratio of fluidized bed diameter to fluidized bed height is set to be constant in the scale-up process.

The effect of geometry size on the thermal stability of the fluidized bed is considered in the present work.The scaling ratios of the fluidized bed diameter are based on the geometry size of a commercial fluidized bed reactor with a bed diameter of 3.05 m.The open-loop thermal stability and closed-loop thermal stability of FBRs are investigated.The details of thermal stability and their similarity in the scale-up process will be discussed later.

3.1.Thermal stability similarity of open-loop control reactor

3.1.1.Effect of catalyst feed rate and liquid feed rate

The thermal stability of open-loop controlled FBRs reflects the intrinsic dynamics characteristics of FBRs.In our previous work[31],the effects of the condensed agent volatility and the condensed agent content in the recycle stream on the open-loop thermal stability of a liquid-containing fluidized bed are investigated.The results showed that the steady-state curves have significant changes along with the condensed agent content.Both the stable branches,Hopf bifurcation points,and multiplicity of the steadystate curves have strong relationships with the liquid content of the recycle stream.What’s more,the liquid feed rate is the main way to reinforce the production rate of FBRs,which is the socalled condensed mode operation.Therefore,the liquid feed rate is one of the most important operating parameters in this section.

The Hopf bifurcation point appears when there is one pair of pure imaginary conjugate roots of the Jacobian matrix of nonlinear differential equations.As the Hopf bifurcation is directly related to periodic oscillation phenomena,temperature runaway will happen when the state of a chemical reaction system is near Hopf bifurcation points.Therefore,the Hopf bifurcation is one of the most important issues for the thermal stability analysis of the FBRs.In the present work,the results and discussion are mainly on Hopf bifurcation points.

The condensed medium is 1-hexene with a density of 650 kg∙m-3.The recycle gas flow rate is approximately 400 t∙h-1for a fluidized bed with a diameter of 3.05 m.For a fluidized bed reactor under the condensed mode operation,the condensed liquid in the recycle gas is in the range of 0 to 20% (mass).Here only the fluidized bed under the condensed mode operation is discussed.Therefore,the liquid feed rates are set to 7.768,12.95,and 19.42 L∙s-1,respectively.The effects of the liquid feed rate on the steady-state curves and multiplicity are shown in Fig.2.The solid lines denote stable branches of the steady state whereas the dash lines refer to unstable ones.And Hopf bifurcation points are denoted by solid dots in Fig.2.In conditions of 310–370 K,which is the actual temperature range in operation,it is observed that all the steady-state curves are divided by HBPs into two parts:a stable branch with low reactor temperature and an unstable branch with relatively high reactor temperature,respectively.In addition,multiple steady states are observed when the liquid feed rate is 19.42 L∙s-1.In the following section,the state variables and operation parameters,and the STY of FBRs at Hopf bifurcation points are plotted in Fig.3 to Fig.8.The effects ofSDon the thermal stability of FBRs are discussed,whereSDis defined as the scaling ratio of bed diameter.

Fig.3. Effect of scaling ratio on the ethylene concentration in the fluidized bed at Hopf bifurcation points.

The scaling ratios are set to 0.1,0.5 and 1.5.Hence the diameters of FBRs investigated in this work are 0.305,1.525,3.05,and 4.575 m,respectively.Effects of the scaling ratio on the concentration of ethylene in the emulsion phase are shown in Fig.3.The modified liquid feed rate is the ratio of the actual liquid feed rate to the square of the scaling ratio of bed diameter.The concentration of ethylene in the fluidized bed is relatively higher when the scaling ratio is relatively low.For one thing,the bubble diameter is small and the mass transfer coefficient between the bubble phase and the emulsion phase is large.Therefore,more ethylene is transferred from the bubble phase to the emulsion phase.For another thing,the heat transfer coefficient between the bubble phase and the emulsion phase is relatively large for small bubbles,then more of the ethylene polymerization heat can be removed by the bubble phase,and the reaction temperature is relatively low when the scaling ratio is small.Consequently,the ethylene concentration in the fluidized bed is higher for a small FBR.In addition,the ethylene concentration increase along with the modified liquid feed rate.As the fluidized bed reactor is under open-loop control,increasing the liquid feed rate causes the increasing heat removal by the condensed liquid and the decrease of reactor temperature.Therefore,increasing the liquid feed rate will lead to an increase in the ethylene concentration for a fluidized bed under the openloop control.

The relationship between the emulsion phase temperature and fluidized bed size at Hopf bifurcation points is illustrated in Fig.4.It is observed that the scaling ratio of bed diameter has little effect on the emulsion phase temperature at Hopf bifurcation points.However,the modified liquid feed rate has a significant effect on the emulsion phase temperature.The emulsion phase temperature decreases linearly along with the modified liquid feed rate in a certain range.For a fluidized bed reactor under the condensed mode operation,the heat release of the polymerization reaction is removed by the recycle flow in two ways: the heat removal by the sensible heat and the heat removal by the latent heat.Increasing the heat removal by the condensed liquid will result in a decrease in the emulsion phase temperature.It should be noted that the Hopf bifurcation point may disappear when the liquid feed rate is too high [31].In addition,the phenomena of defluidization of FBRs under the open-loop control may occur,especially when the condensed medium has a relatively higher boiling point.

In Fig.5,the relationship between the modified catalyst content and the modified liquid feed rate with different scaling ratios at Hopf bifurcation points is depicted.The modified catalyst contentis the product of the actual catalyst content and the scaling ratio of the bed diameter.The simulation results in Fig.5 show that the modified catalyst content decreases along with the scaling ratio of the bed diameter.As it has been discussed above,the production rate of a small fluidized bed reactor is lower due to the lower reactor temperature.The liquid feed rate has a significant effect on the catalyst content under the open-loop control strategy.It’s observed that the modified catalyst content increases sharply along with the modified liquid feed rate.The similar trends in the state variables(i,e.the ethylene concentration,the reactor temperature,and the catalyst content) at Hopf bifurcation points reveal the similarity of thermal stability in the scale-up process of FBRs.

Fig.4. Effect of scaling ratio on reaction temperature at Hopf bifurcation points.

Fig.5. Effect of scaling ratio on the modified catalyst content in the fluidized bed at Hopf bifurcation points.

The modified catalyst feed rate is defined as the ratio of the catalyst feed rate to the scaling ratio of the fluidized bed diameter.The effect of the scaling ratio on the modified catalyst feed rate at Hopf bifurcation points is shown in Fig.6.For the fluidized bed reactors with a smaller diameter,the residence time of the particle is longer,while the modified catalyst content is larger,thus the modified catalyst feed rate is lower.So,it can be concluded that the residence time of catalyst particles or the polyethylene particles is longer for smaller FBRs under the open-loop operation.In addition,the modified catalyst feed rate increases along with the modified liquid feed rate.A similar trend in the catalyst feed rate reveals the similarity of the operating parameters in the scale-up of FBRs.

The capital costs and maintenance costs of FBRs will be greatly reduced by improving STY.In Fig.7,the effect of the scaling ratio on the STY of FBRs at Hopf bifurcation points is illustrated.The modified STY is defined as the product of the actual STY and the scaling ratio of bed diameter.When the scaling ratio is 0.1,the modified STY is the lowest for a given modified liquid feed rate.In addition,it is shown that the modified STY of polyethylene decreases along with the modified liquid feed rate at Hopf bifurcation points in Fig.7.Due to the lower reactor temperature,a larger liquid feed rate will result in a lower STY.Besides,similar trends in the modified STY at Hopf bifurcation points are observed.

Effect of liquid feed rate has little effect on STY at Hopf bifurcation points as shown in Fig.7.In order to investigate the effect of the scaling ratio of bed diameter on the STY at Hopf bifurcation points,the average values of the actual STY are calculated and depicted in Fig.8.It is clearly shown that the average STY is inversely proportional to FBRs’geometry size at Hopf bifurcation points.For the scale-up of FBRs,the hydrodynamic similarity laws are applied.Therefore,the bed height is proportional to the bed diameter.The heat removal capacity of recycle flow is proportional to the square of the reactor diameter,while the production rate is proportional to the cube of the reactor diameter.Finally,it is con-cluded that the STY of FBRs is inversely proportional to the scaling ratio of bed diameter.

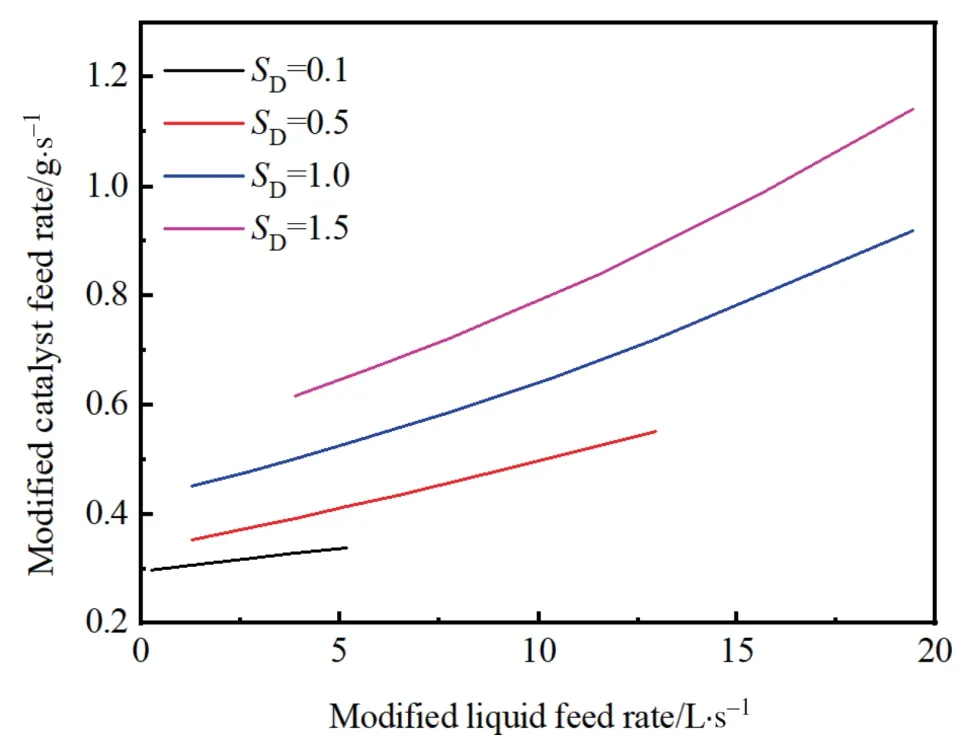
Fig.6. Effect of scaling ratio on the modified catalyst feed rate at Hopf bifurcation points.

Fig.7. Effect of scaling ratio on STY at Hopf bifurcation points.

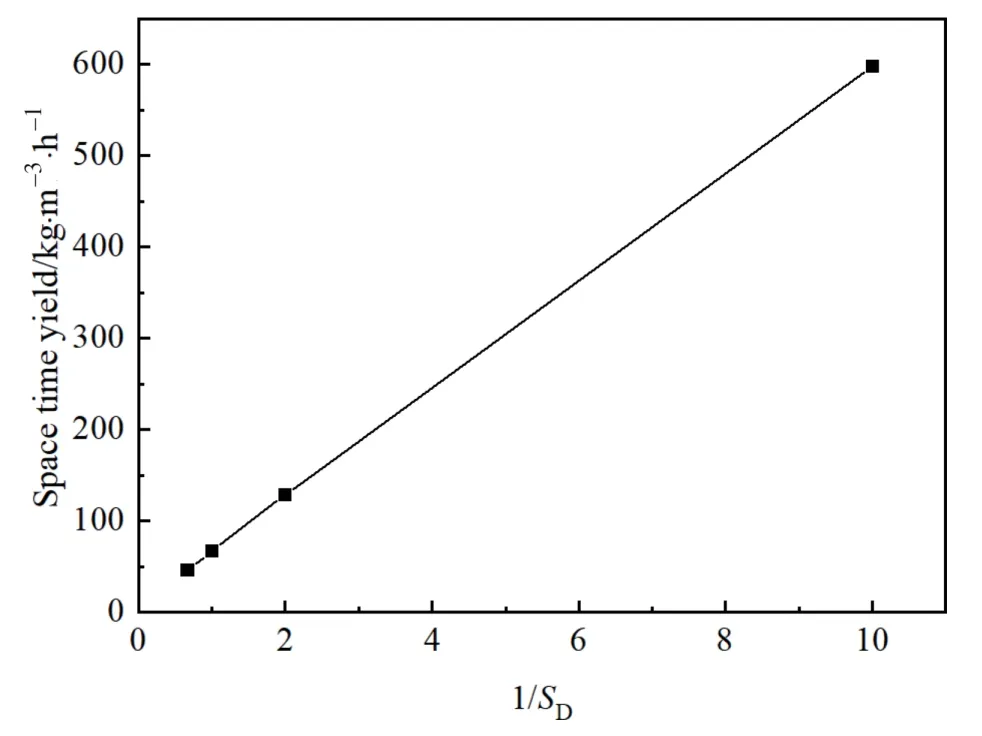
Fig.8. Relationship between STY and scaling ratio at Hopf bifurcation points.

The concentrations of ethylene,nitrogen and hydrogen have little change along with the liquid feed rate,while the conversion of 1-hexene is very low.It is reasonable to assume that the composition of the recycle stream is approximately constant.Furtherly,the thermal stability of FBRs under the condensed mode operation is mainly determined by the energy balance equations and the mass balance equation of the catalyst.

3.1.2.Effect of activation energy

In the above section,the effects of the scale ratio of bed diameter on the Hopf bifurcation curves have been discussed in the panel of the catalyst feed rate and the liquid feed rate.To investigate the effect of the polymerization kinetics parameters on thermal stability,the activation energy of the chain propagation rate constant is applied as a parameter,whereas the catalyst feed rate is another one.As shown in Fig.9(a),the Hopf bifurcation curves on the panel of the activation energy and the catalyst feed rate have similar trends.In Fig.9(b),the catalyst feed rate is modified and the Hopf bifurcation curves are very similar.

The STY of FBRs at Hopf bifurcation curves in Fig.9 are calculated and depicted in Fig.10.It is observed that the modified STY curves are very close when the modified STY values are higher and the scale ratio is larger than 0.5.When the modified STY is below 200 kg∙m-3∙h-1),the Hopf bifurcation curves still have the same trend.However,the modified catalyst feed rate varies in a relatively large range for a given modified STY.

Fig.10. The Hopf bifurcation curves on the panel of the modified STY and the modified catalyst feed rate.

3.2.Thermal stability similarity of closed-loop control reactor

For the open-loop strategy of the ethylene polymerization in the FBRs,there exists a Hopf bifurcation point which results in temperature oscillation and even temperature runaway.According to the above discussion,the similarity in thermal stability of open-loop controlled FBRs with different scales is investigated.In the next section,the thermal stability similarity of closed-loop controlled FBRs will be investigated.The most conventional controllers used in chemical engineering are the proportional-integral control (PI) and the proportional-integral-derivative control (PID).The control system for the ethylene polymerization process is quite complex,consisting of the cascade control system for the reactor temperature and pressure,the ratio control system for the concentration of reactant,etc.To find the thermal stability similarity of the closed-loop controlled FBRs,the PI controller for the reactor temperature is selected.The control law of the PI control is expressed as:

Fig.9. The Hopf bifurcation curves on the panel of the activation energy and the catalyst feed rate.

WhereTgis the temperature of the recycle stream return to the bottom of FBRs,Tg,0is the set value of the controlled variableTg,Tsis the set value of the reactor temperature,Teis the measured reactor temperature,ε is the error between the actual value and the set point.

Compared with the open-loop system,the state variable reactor temperature is well controlled by the PI controller.The reactor temperature always converges to the set point.The effect ofKPon the stability of FBRs is shown in Fig.11.Hopf bifurcation points are represented by solid dots.For the cases ofKP=0.5 and 1.0,the steady-state curves consist of two parts: a stable branch denoted by the solid line and an unstable branch denoted by the dashed line,respectively.For a commercial fluidized bed reactor with a diameter of 3.05 m,the catalyst feed rate is approximately 0–0.8 g∙s-1.Therefore,the reactor temperature is well controlled whenKPis higher than 0.5.In accordance with the effect of fluidized bed diameter on the thermal stability of the open-loop system,increasing the fluidized bed diameter helps expand the stable branch.

In Fig.12,the closed-loop stability behavior of FBRs as shown in Fig.11 is summarized.The scaling ratios of bed diameter are set as 0.5,1.0,and 1.5.The Hopf bifurcation curves in Fig.12(a)have similar trends.It is observed that the controller parameterKPincreases along with the actual catalyst feed rate.However,actual values of the catalyst feed rate are obviously different especially when theKPincreases to a relatively high degree.In Fig.12(b),the Hopf bifurcation curves are replotted with the modified catalyst feed rate as abscissa.It is observed that the Hopf bifurcation curves are similar,which reveals thermal stability similarity in the scale-up of the closed-loop system.

The introduction of the PI controller changes the equilibria of reaction systems and the PI control parameters have an influence on the stable region [40].The Hopf bifurcation curves are plotted out in Fig.13 withKPand τ as the coordinates in order to investigate the effects of PI control parameters on the thermal stability similarity.As shown in Fig.13,KPvaries from 0.7 to 10.0,whereas τ varies from 0.4 to 2000 s.The solid star represents PI control parameters applied to a commercial fluidized bed reactor 3.05 m in diameter withKP=1.5 and τ=468 s.As the actual PI control parameter is far away from the Hopf bifurcation curves,the fluidized bed reactor is well controlled.In addition,the similar trend of the Hopf bifurcation curves with different scale ratios proves the similarity of thermal stability of closed-loop controlled FBRs.At last,it should be noted that although increasingKPwill enlarge the stable region with a significant increase of the upper boundary of the catalyst feed rate,however,the temperature of recycle flowshould be considered.Anyway,the recycle flow temperature must be higher than the cooling water temperature.

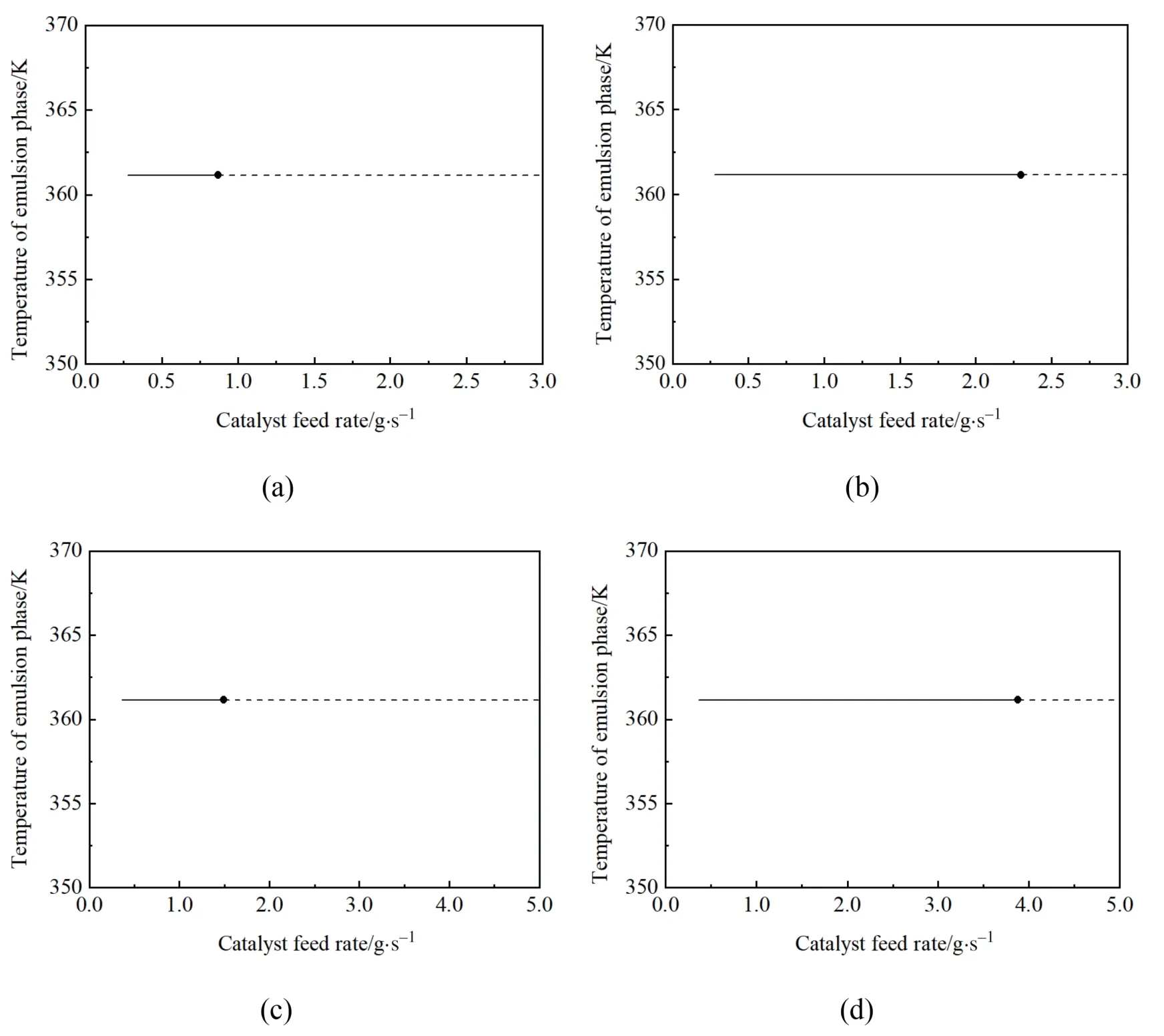
Fig.11. Effect of KP on closed-loop stability(Ea=37.67 kJ∙mol-1,τ=360 s):(a)KP=0.5,Lin=25.89 L∙s-1,SD=1.0;(b)KP=1.0,Lin=25.89 L∙s-1,SD=1.0;(c)KP=0.5,Lin=58.24 L∙s-1,SD=1.5;(d)KP=1.0,Lin=58.24 L∙s-1,SD=1.5.The solid line‘‘-”denotes stable branch,the dash line‘‘---”denotes unstable branch,the filled circle denotes Hopf bifurcation point.

Fig.12. The Hopf bifurcation curves on the panel of KP and the catalyst feed rate (Ea=37.67 kJ∙mol-1,τ=360 s, Lin=58.24 L∙s-1).

Fig.13. The Hopf bifurcation curves on the KP-τ panel (Ea=37.67 kJ∙mol-1,modified Fcat=0.418 g∙s-1, Lin=25.89 L∙s-1,★: industrial data).

4.Conclusions

In the present paper,a multi-zone model consisting of the twophase model and the liquid evaporation model is proposed to illustrate the ethylene polymerization in FBRs under the condensed mode operation.A set of scaling laws is proposed based on the Glicksman scaling laws and is testified by the thermal stability similarity with Hopf bifurcation points as criteria.

With the proposed scaling laws,the thermal stability of the open-loop controlled and closed-loop controlled FBRs in different bed diameters are investigated.For the open-loop controlled FBRs,similar trends in the state variables,the system parameters,and the STY at Hopf bifurcation points are observed which indicates the similarity of thermal stability.For the closed-loop controlled FBRs,a conventional proportional-integral controller is applied to control the reactor temperature.The Hopf bifurcation curves of the closed-loop control system in the two parameters panel also show the thermal stability similarity.

The relationship between the STY of FBRs and operation parameters at Hopf bifurcation points is obtained by the detailed multizone model.It can be concluded that the thermal stability of FBRs under the condensed mode operation is mainly determined by the energy balance equations and the mass balance equation of the catalyst.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors gratefully acknowledge financial supports from the Project of the National Natural Science Foundation of China(22178304,22108239) and the Start-up Funding of Ningbo Research Institute of Zhejiang University (20201207Z0204).

Nomenclature

ARcross-sectional area of reactor,m2

Ciconcentration of componenti,mol∙L-1

Cp,gspecific heat of recycle gas,kJ∙kg-1∙K-1

Cp,lspecific heat of condensate,kJ∙kg-1∙K-1

Cp,sspecific heat of polyethylene,kJ∙kg-1∙K-1

Dreactor diameter,m

Eaactivation energy,J∙mol-1

gacceleration constant,m∙s-2

Hfluidized bed height,m

Hbeoverall coefficient of heat exchange between bubble and emulsion phase,W∙m-3∙K-1

ΔHRheat of reaction,kJ∙kg-1

ΔHvlatent heat of evaporation,kJ∙kg-1

Kbeoverall coefficient of gas exchange between bubble and emulsion phase,s-1

KPproportional constant for the system called gain

kddeactivation constant of catalyst,s-1

kp,0reaction rate constant of monomer at reference temperature,L∙mol-1∙s-1

kp,ireaction rate constant of monomeri,L∙mol-1∙s-1

Lvolume of condensate in G-L-S zone,L

Linmass flow rate of condensate injected into fluidized bed reactor,L∙s-1

Mw,imolecular weight of componenti,g∙mol-1

Preactor pressure,kPa

Qevolumetric product withdrawal rate,m3∙s-1

Qssolid exchange rate,m3∙s-1

qccatalyst feed rate,kg∙h-1

SDscale-up ratio of bed diameter

Teemulsion phase temperature,K

Tfrecycle gas temperature,K

Trefreference temperature,K

TSset value of the reactor temperature,K

Ubvelocity of a bubble rising through a bed,m∙s-1

Ueupward velocity of gas through emulsion phase,m∙s-1

Umfsuperficial velocity at minimum fluidizing conditions,m∙s-1

U0superficial gas velocity,m∙s-1

Xccatalyst content in a PE particle,g∙g-1

δ*relative fraction of bubble phase

δlliquid film thickness,m

ε error between the actual value and the set point

εjvolumetric fraction of zonej

εmfbed voidage at minimum fluidizing conditions

μgviscosity of gas,Pa∙s

ρcatdensity of catalyst,kg∙m-3

ρgdensity of recycle gas,kg∙m-3

ρldensity of condensate,kg∙m-3

ρsdensity of polymer particle,kg∙m-3

τ integral time

φ sphericity of a particle