A pseudo transient nonequilibrium method for rigorous simulation of multicomponent separation columns

Jie Wu ,Yiqing Luo,2,3,,Xigang Yuan,2,3

1 School of Chemical Engineering and Technology, Tianjin University, Tianjin 300350, China

2 Chemical Engineering Research Center, Tianjin University, Tianjin 300350, China

3 State Key Laboratory of Chemical Engineering, Tianjin University, Tianjin 300350, China

Keywords:Nonequilibrium stage model Pseudo-transient continuation Distillation Numerical simulation Systems engineering

ABSTRACT Nonequilibrium stage model is a significant improvement in multicomponent separation process simulation,but more equations are involved and the solution of the model equations,which relies on an adequate initial guess for convergence of the Newton method,is difficult.In this work,based on the concept of pseudo-transient continuation approach,we proposed a new pseudo-transient (PT) nonequilibrium method.The proposed method decouples the strongly coupled model equations by introducing dynamic equations for material and energy conservation,as well as transition equations.Thus,the steady-state solution of the nonequilibrium stage model can be obtained through a robust and fast integration process,and the initial guess issue in Newton method can be effectively avoided.Two simulation cases were used to demonstrate the advantages and applicability of the proposed PT nonequilibrium method.

1.Introduction

The widely used equilibrium stage models for multistage separation simulations assume that thermodynamic equilibrium is achieved at each stage of a distillation column.As the equilibrium stage model is often far from reality,Murphree vapor-phase tray efficiency models are usually incorporated to approximate equilibrium stages to actual stages.However,Murphree efficiencies cannot be easily estimated and the available Murphree efficiency correlations were shown valid only for binary mixtures or closeboiling and ideal multicomponent mixtures [1],but not for nonideal multicomponent mixtures,where the interactions between mass transfers of different components lead to different deviations from the equilibrium for the different components [2].

To overcome such a difficulty in the multicomponent separation simulation,Krishnamurthy and Taylor[3]proposed their first generation nonequilibrium stage model in 1985,referred to as the rate-based model.In their model,rate equations based on the two-film mass transfer model are used to characterize the interphase mass transfers of components and the heat transfer with the assumption of phase equilibrium at the vapor–liquid interface instead of equilibrium between the vapor and liquid phases.The mass and heat transfer coefficients can be calculated from various correlations for different tray or packing types inner a column.In 1994,Tayloret al.[4]took hydraulic calculation into consideration and proposed the second generation nonequilibrium stage model,which found wider applications ever since[4–8]and demonstrated its potential for accurate design and optimization of multicomponent separation processes.However,as many correlations for the rate models,which are usually nonlinear equations,for the mass and heat transfers must be included,the computation for solving the large-scale non-linear equations of nonequilibrium stage models remains challenging and limits its applications of the nonequilibrium stage model.

The strategies of solving nonequilibrium stage models has been widely investigated,with a number of approaches developed.One such approach is equation partitioning,which partitions the nonequilibrium equations and solves one or one group at a time by an equation-tearing method.In Wanget al.[9],the simulation problem of an air separation process was solved successfully by the equation partitioning method.However,this method has a significant computational cost owing to its mass of iterations,and the initial guess must be selected carefully in order to avoid the failure of convergence.Another approach is simultaneous-correction,which solves all the equations of nonequilibrium stage model simultaneously.The Newton–Raphson (NR) method is the most widely used in the simultaneous-correction approach,which usually requires solving the equilibrium stage model of the same process at first to get good initial estimates of some important variables[8,10–14].However,it cannot ensure that the solution of the equilibrium stage model is always a good initial estimate for nonequilibrium stage model,and additional initialization calculations are time-consuming.Another kind of simultaneouscorrection approach is homotopy/continuation(HC)[14,15],which has been used to solve difficult algebraic equation models in chemical engineering process simulation and design problems.HC starts with a set of easily solvable equations and then gradually transitions to the original equations through a transition path.There are studies demonstrated that the HC method is more efficient than the NR method [14,16].However,this method also needs some additional initialization steps.

All the above methods for solving the nonequilibrium stage model,especially the Newton method,relies heavily on initial guess.In order to obtain a good initial guess,all these methods require an initialization procedure,using the simulation results of the equilibrium stage model or a simplified calculation based on some assumptions to assign initial values to the nonequilibrium stage model,which is undoubtedly time-consuming and,more importantly,cannot be guaranteed to work for all kinds of distillation processes.Thus,the convergence of nonequilibrium stage model has become an important issue,especially for the cases,like optimization,where simulations are repeatedly used for different values of decision variables.In this study,we proposed a pseudotransient (PT) nonequilibrium method to handle this problem.The remainder of this paper is organized as follows:Section 2 presents the PT nonequilibrium method.In Section 3,two cases,which includes a simple depropanizer column and a complex methyl acetate (MAC) reactive distillation column,are studied to demonstrated the accuracy and robustness of the PT nonequilibrium method.In Section 4,we conclude our work.

2.Model Equations

In this study,the basic idea of the proposed method is to apply the concept of pseudo-transient continuation method to complex processes modeling,which was also applied in Pattison and Baldea[17] and Maet al.[18].By this method,the algebraic equations of the nonequilibrium model are transferred into differential and algebraic equation (DAE) system.The DAE model can effectively decouple the conservation equations of material and energy by introducing dynamic equations,and transform the initial guess problem of solving a large-scale nonlinear system of algebraic equations by a Newton method into a more easily solvable initial condition problem of the DAEs,in case of the Newton method fails to converge.In addition,by introducing transition equations,the solving process starts from solving the equilibrium model first,and gradually transitions to solving the non-equilibrium model,which greatly reduces the solution difficulty.With these two means,the nonequilibrium model can be solved robustly.

2.1.Dynamic equations and Pseudo-hold-up correlations

Fig.1 presents a schematic diagram of a nonequilibrium stage in a certain column section.The vapor and liquid mass transfer rates of componention stagejsatisfy Eq.(1),and the component material conservations in vapor and liquid phase bulk are descripted by Eqs.(2) and (3) respectively.Thus,component material conservation on stagejcan be derived from Eqs.(1)–(3),and Eq.(4) is obtained.

whereLjandVjare the liquid and vapor molar flow rates of streams leaving stagej.xi,jandyi,jare the liquid and vapor component molar fractions of the streams.andare the liquid and vapor mass transfer rates of componention stagej,respectively.

Now we transform Eq.(4)into the following dynamic equation:

whereMi,jis the molar hold-up of componention stagej,andtis the pseudo-transient time,or simply referred as the integration time.

The same transformations are also extended to the equations about energy conservation.

whereandare the liquid and vapor molar enthalpy of streams leaving stagej,respectively,Hjis the total enthalpy of the hold-up on stagej.

The other energy conservation equations are shown below.

Heat transfer rate conservation:

Vapor-phase energy conservation:

Liquid-phase energy conservation:

whereandare heat transfer rates between vapor bulk and phase interface,and liquid bulk and phase interface,respectively.

By transforming the material conservation and energy conservation equations from algebraic equations into differential equations,the variables on adjacent stages can be decoupled,and making the model relatively easy to solve.In addition,because what concern us is the steady-state solution rather than the variation of the dynamic process,there is no need to get the true values of the liquid hold-up and its enthalpy on each stage based on rigorous tray hydraulic correlation,but only use the simple pseudo hold-up correlation proposed and defined by Maet al.[18],as shown in the Eqs.(10)–(13),which does not change the steadystate solution and allows us to obtain the solution by simple integration.

Fig.1. Schematic diagram of a nonequilibrium stage.

Pseudo-hold-up correlations:

whereandare the total vapor and liquid molar hold-up on stagej.CVandCLare the constant coefficients,which are recommended to be 1800 h-1in Ref.[18].

2.2.Transition equations

Although the material and energy conservation equations of adjacent stages are decoupled by Eqs.(5) and (9),due to the nonlinearity of these conservation equations,they remain difficult to converge if the initial estimates of flow rates,temperatures,mole fractions of liquid and vapor are not close to the solution.Inspired by the fact that the result of equilibrium model is a relatively good initial guess for solving nonequilibrium model,we proposed following transition equations to achieve robust solution of the process model.

2.3.Mass transfer rate and heat transfer rate equations

To deal with multicomponent mass transfer in the nonequilibrium model,the Maxwell-Stefan approach was adopted,as shown in Eqs.(22) and (23).

j=1,2,∙∙∙,Ns;k=1,2,∙∙∙,Nc

where,yIand xIare the column vectors of component mole fractions of the vapor and the liquid at the interface,yIand xbulkare the column vectors of component mole fractions of the vapor and the liquid phase bulks,NVand NLare the column vectors of vapor and liquid component mass transfer rates respectively,[kV] and[kL] are the matrices of vapor and liquid mass transfer coefficients respectively.According to the Maxwell-Stefan approach,the dimension of these vectors isNc-1 and the dimension of these matrices is (Nc-1)×(Nc-1).In order to make the system of equations solvable,the summation equations need to be included.

[kL] and [kV] are calculated by:

where the elements of matrix [R]jis calculated as follows:

where,kiNc,kikandkilare binary mass transfer coefficients,andais the total interfacial area for mass transfer.is the matrix of thermodynamic factors,and its elements are estimated by:

The heat transfer rate equations are

The heat transfer coefficient,ht,is estimated through the Chilton-Colburn analogy:

2.4.Pressure-drop correlation

A pressure profile in a column is necessary to model the industrial distillation column.In this study,the pressure-drop correlation of sieve tray proposed by Bennettet al.[19] was applied.And it is composed by three parts: pressure drophLcaused by the liquid inventory,hdby dry tray perforation,andhσby the surface tension.

In summary,the PT nonequilibrium method proposed in this study consists of the following equations:

When dealing with reactive distillation problems,as the reactions may take place on each stage,the dynamic component material conservation Eq.(5) is replaced by a new dynamic equation:

whereris the reaction rate,and Voljis the liquid volume of reaction on stagej.The reaction is assumed to take place only in liquid holdup and Voljis approximately given by Eq.(38):

At the beginning of solving the PT nonequilibrium model,the liquid molar hold-upand the component molar hold-up(Mi,j) are given as the initial conditions of Eqs.(5) and (9) respectively.The whole solution procedure consists of two steps,consistent initialization and time integration.The detailed description of the two steps is available in Pattison and Baldea [17].In the next section,two example cases are used to illustrate the proposed PT nonequilibrium method.

3.Method Validation

Two distillation processes,namely a depropanizer and a methyl acetate reactive distillation column,were simulated to validate the proposed PT nonequilibrium method.Both cases were performed on a desktop with Intel(R) Core (TM) i7-6700CPU at 3.40 GHz.Table 1.

3.1.Case 1: Depropanizer

The depropanizer is a part of the separation process in ethylene production,which separates the components below C3and above C4.Tayloret al.[4]also simulated this example case based on their second generation nonequilibrium model.In order to ensure the accuracy of our model,we kept the same thermodynamic model,physical property model and the column’s structure parameters as those in Tayloret al.[4].The thermodynamic model used in this example case is Peng-Robinson cubic EOS.The tray type is sieve tray,and Zuiderweg mass transfer correlation was used to calculate the binary mass transfer coefficients and the total interfacial area for mass transfer.Specifications for the column and trays are listed in Table 2 and Table 3 respectively.Column’s operating conditions parameters and feed stream parameters are listed in Table 4.The schematic diagram of the column is shown in Fig.2.

The integrator used here was Implicit Euler and the computing time of the simulation using the proposed PT nonequilibrium method was 50 s.The results of the product streams are shown and compared with the results of Taylor’set al.[4] in Table 5.

As shown in Table 5,the solutions of the PT nonequilibrium method are nearly the same as those of the second generation nonequilibrium model of Taylor’set al.,except for numerical error in the very small mole fractions.The result illustrates the accuracy of the PT nonequilibrium method.

To compare the robustness of the Newton method which was used to solve the second generation nonequilibrium model of Taylor’set al.[4]and the PT nonequilibrium method presented in this study,we selected six sets of initial guesses for simulation test.As shown in Table 6,initial guesses(1)–(4)cover the range of the flow rates (L,V) and temperatures (T) of the simulation results by nonequilibrium model for each stage along the column,initial guess (5) is obtained by solving equilibrium stage model,and initial guess (6) is an inferior initial guess,which is far away from the solution.The results of simulating with the six different initial guesses show that Newton method failed to converge for almost all the initial guesses,except for initial guess (5).Obviously,Newton method needs an initial guess very close to the solution,for example,the initial guess (5).In contrast to Newton method,the PT nonequilibrium method successfully converged for all these initial guesses,including the inferior initial guess (6).

It’s worth noting that,just as Powerset al.[14]pointed out,the initial guess solved by equilibrium stage model is usually valid only for small problems (few stages and few components) and weakly nonlinear problems (ideal mixtures),such as the depropanizer in case 1,but not suitable for large scale (large number of components and column stages) or strongly nonlinear (nonideal mixtures) problems.However,this problem can be solved by PT nonequilibrium method using the initial conditions of differential variables rather than a good initial guess.In fact,in the consistent initialization step at the beginning of the PT method solving process,we only need to set the initial conditions ofMi,jandappropriately,that is,the initial conditions ofMi,jandare generally set to makeLi,jandVi,jare of the same order of magnitude as that of the feed streams.After that we can proceed to a rapid integration step and obtain the steady-state solution.

The advantage of avoiding relying on initial guesses enables the proposed PT nonequilibrium method to solve not only small problems,but also large scale or strongly nonlinear problems.To test this ability,we extended the application of the PT nonequilibrium method to a reactive distillation in the next subsection.

Table1 Summary of equations

3.2.Case 2: Reactive distillation

Reactive distillation (RD) is a kind of process intensification technology which integrates separation and chemical reaction processes into one distillation column.However,the coupling of reaction and separation makes it difficult to solve the model equations of RD processes,especially when the trays inner the column are modeled as nonequilibrium stages.In this section,the methyl acetate (MAC) homogeneous RD process studied by Liet al.[20] was investigated.Liet al.simulated and optimized the homogeneous MAC RD process based on equilibrium model.Referring to the optimal design results of Liet al.,we re-evaluated the design using the proposed PT nonequilibrium method.

MeOAc and H2O are the products of the esterification reaction of HOAc and MeOH.This reaction is reversible and shown as follows.

The reaction kinetic model for this reaction is:

ris the reaction rate.α is the activity of each component.The parametersKeqandkfare given in Eqs.(40) and (41):

The parameters needed for the calculation of activities and the calculation method can be found in Husset al.[21].

The Wilson equation was used as the thermodynamic model.The tray type is also sieve tray and Zuiderweg mass transfer correlation was used.Fig.3 presents the schematic diagram of this RD column.The column and tray parameters taken from Liet al.[20]are listed in Tables 7 and 8,respectively.Table 9 shows the feed stream and column operating conditions.Table 10 shows the simulation results.

To compare the ability and robustness of Newton method and PT nonequilibrium method when dealing with large-scale problems,we also chose six different sets of initial guesses for simulation test.As shown in Table 11,initial guesses (1)–(4) cover the range of solution by nonequilibrium model,initial guess (5) is the simulation results of equilibrium stage model,and initial guess(6) is far away from the solution.The results showed that Newton method failed to converge at all initial guesses,even at the relatively good guess (5),while PT nonequilibrium method converged successfully at every initial guess.

Besides,in Li’set al.[20],there were requirements for product purity and reactant conversion,which require the MeOAc purity in distillate was more than 98%(mass)and the conversion of materials was more than 95%.However,when we evaluated their results using PT nonequilibrium method,the purity of the top product 88.71%(mass)(i.e.77.22%(mol))and the reactant conversion 69.57% (mol) were obtained,both of which did not meet the requirements.Fig.4 shows the profile of Murphree vapor trayefficiencies estimated based on the simulation results by the PT nonequilibrium method.It is easy to find that the Murphree vapor tray efficiencies of almost all components on each stage are around 0.6 except for two component point efficiencies lying outside the range of [0,1],which is supposed to an effect of diffusion interaction,as explained by Tayloret al.[5,22].

Table2 Specifications for column

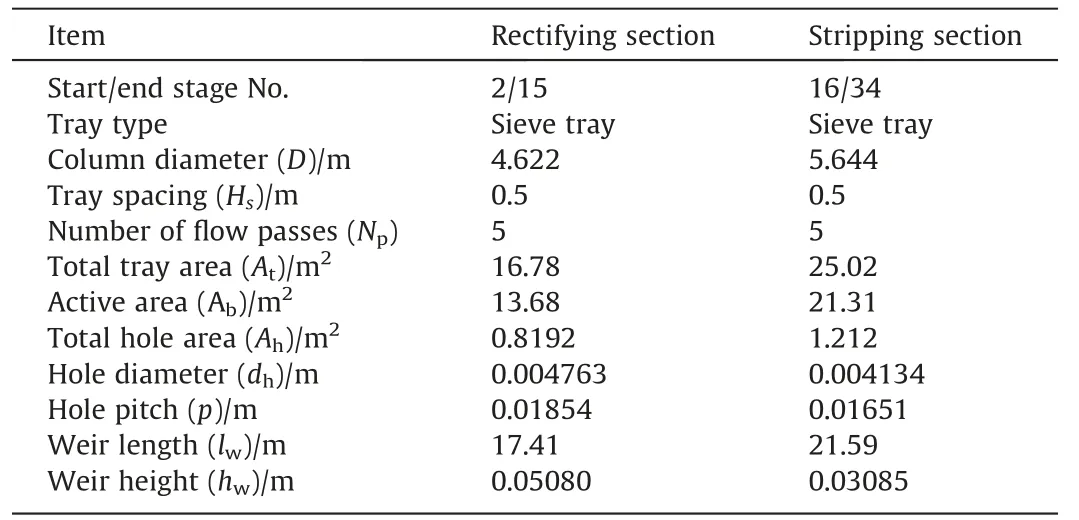
Table3 Specifications for column tray

Table4 Parameters for operating and feed stream

Fig.2. Schematic diagram of the depropanizer.

Table5 Stream results

The results of this example show that the simulation results of the equilibrium model are not reliable and it is necessary to design the distillation column based on the nonequilibrium phase model.Besides,compared with nonreactive distillation,the model of reactive distillation needs to incorporate reaction kinetic model based on the two-film mass transfer model,resulting in a large-scale system of strongly coupled nonlinear equations.Therefore,the simulation of reactive distillation is more difficult than the nonreactive distillation.However,the proposed PT nonequilibrium method still shows very strong robustness and high efficiency when dealing with reactive distillation,and the computing time of case 2 is 55 s.This proves once again the outstanding advantages of the proposed pseudo-transient nonequilibrium method in robust solving ability.

4.Conclusions

Fig.3. Schematic diagram of the MAC RD column.

In this work,a novel pseudo-transient nonequilibrium method was proposed.By introducing dynamic equations to replace subset of algebraic equations together with the transition equations,the very tricky problem of large-scale nonlinear algebraic nonequilibrium model is successfully solved.The proposed PT nonequilibrium method is based on the simulation of dynamic process with a simple pseudo-hold-up correlation,and the nonequilibrium model can be solved easily through integration starting from an initial state far from the problem solution so that the initial guess issue for Newton type method can be completely avoided.Both example cases demonstrated that the proposed PT nonequilibrium method has stable performance and can converges robustly regardless of the scale or the nonlinearity of problems.This work also highlights the importance of accurate design with more rigorous nonequilibrium model by comparing the simulation results between the nonequilibrium and equilibrium model.

Table7 Specifications for column

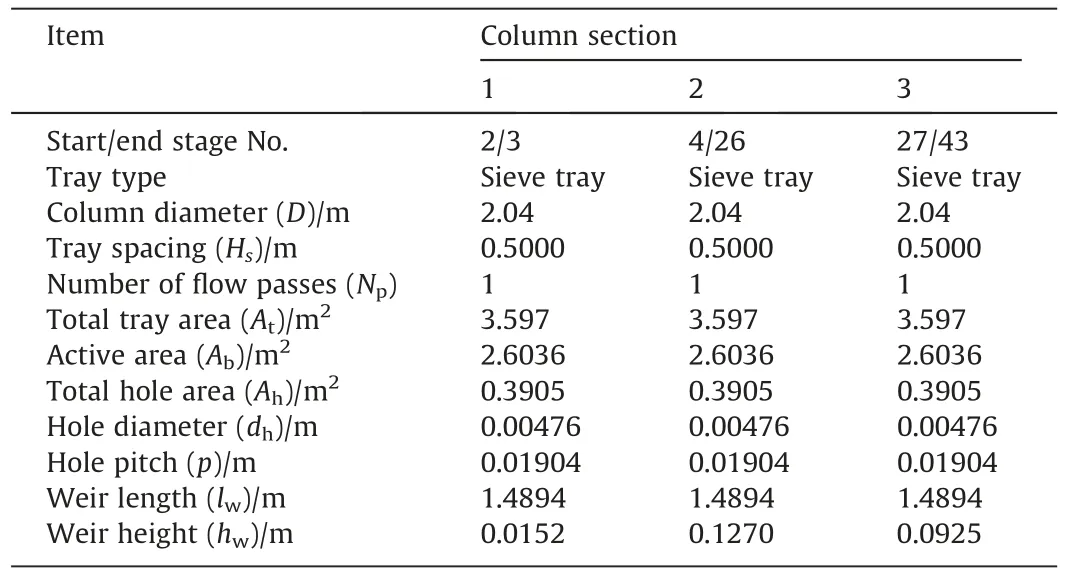
Table8 Specifications for column tray

Table9 Parameters for operating and feed stream

Table10 Stream results

Fig.4. Murphree vapor tray efficiencies.

In addition,the significance of robust and efficient solution of nonequilibrium model is to bring a bright prospect for equationoriented optimization of multi-stage separation equipment based on nonequilibrium model,because the inherent advantage of gradient-based optimization methods lies in that they can obtain the gradient informationviaautomatic or symbolic differentiation,which needs to ensure that the simulation problem is converging at each iteration in the optimization.

Data Availability

Data will be made available on request.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was supported by the National Natural Science Foundation of China (21978203).

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.cjche.2023.04.011.

Table11 Comparison of the convergence performance from different initial guesses

Nomenclature

Subscripts

i,k,lcomponent index

jstage index

Superscripts

I phase interface

L liquid phase

V vapor phase

bulk vapor or liquid bulk