A master–slave generalized predictive synchronization control for preheating process of multi-cavity hot runner system

Hongyi Qu,Shengyong Mo ,Ke Yao ,Zhao-Xia Huang ,Zhihao Xu ,Furong Gao,3

1 Institute of Intelligent Manufacturing, Guangdong Academy of Sciences, Guangdong Key Laboratory of Modern Control Technology, Guangzhou 510070, China

2 Fok Ying Tung Graduate School, The Hong Kong University of Science and Technology, Guangzhou 511442, China

3 Department of Chemical and Biological Engineering, The Hong Kong University of Science and Technology, Hong Kong 999077, China

4 National Engineering Research Center of Novel Equipment for Polymer Processing, Department of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510641, China

ABSTRACT As a key component of injection molding,multi-cavity hot runner(MCHR)system faces the crucial problem of polymer melt filling imbalance among the cavities.The thermal imbalance in the system has been considered as the leading cause.Hence,the solution may rest with the synchronization of those heating processes in MCHR system.This paper proposes a ‘Master-Slave’ generalized predictive synchronization control(MS-GPSC)method with’Mr.Slowest’strategy for preheating stage of MCHR system.The core of the proposed method is choosing the heating process with slowest dynamics as the‘Master’to track the setpoint,while the other heating processes are treated as‘Slaves’tracking the output of‘Master’.This proposed method is shown to have the good ability of temperature synchronization.The corresponding analysis is conducted on parameters tuning and stability,simulations and experiments show the strategy is effective.

1.Introduction

Rapid polymer part application in modern industry requires injection part to be molded consistently,efficiently,and with high precision.For this reason,multi-cavity hot runner (MCHR) system has been widely used in injection molding since it can mold multiple products in a single injection batch.As shown in Fig.1,a MCHR system typically consists of a manifold and multiple nozzles connecting to different cavities.These components are heated by their corresponding heating coils to keep the material passing through them in melting state with a proper temperature.Compared with traditional runner system,MCHR system needs not to have materials in the runner cooled so it can effectively eliminate the residual material(as illustrated in Fig.2)and have better transfer of injection pressure to the cavities.So,MCHR has better production state and economical efficiency.To ensure consistency among parts molded in different cavities,the amount and rate of polymer melt injected through each nozzle to different cavities should be kept the same,so a ‘balanced filling’ can be maintained.The imbalanced filling may lead to the severe consequence that some cavities are over-filled with flash while other cavities are under-filled with short-shot as illustrated in Fig.3.

According to studies leaded by Chenet al.[1],Reifschneider[2],Beaumontet al.[3],imbalanced filling among cavities is mainly attributed to uneven temperature among runners,which may be caused by the shearing of polymer melt through MCHR system as shown in Fig.4.Therefore,the key for a balanced filling is that the temperature of whole MCHR system should be evenly distributed among the runners at a desired value,alternatively called‘setpoint’.Many investigators [4–6] improved and optimized the thermal structure design to achieve even temperature based on runner geometrical design/optimization.Those reports did not consider temperature control of heating processes in the MCHR system.

The control of heating processes in MCHR system is not a new research topic since its primitive research can be dated back to 1980s[7].Most of the concerned researches are focus on the thermal structure[8–10],hardware[11–13]of MCHR.In aspect of control algorithm design,although there have been plenty of researches on tackling temperature control algorithm design problem for various specific occasions based on PID,model predictive control(MPC),neural networks controletc.[14–16],there are only few works on the temperature control algorithm specified for hotrunner system[17,18].Moreover,considering the unique feature of the MCHR processing procedure,it is hard to directly using above knowledge in the heating control of MCHR.In MCHR system,the heaters are respectively located at inlet,manifold,nozzlesetc.Their heating processes couple with each other due to complicated heat transfer phenomena which is difficult to be modeled and results in process uncertainties in addition to their standalone process dynamics.Such process property makes the temperature controller design for MCHR system a challenging task.

Fig.1. Multi-cavity hot runner system.

This paper focuses on the temperature control of MCHR system at preheating stage during which the temperature is heated up to the setpoint without any polymer melt inside MCHR system before the injection molding process begins.It is obvious that the even temperature distribution in MCHR system at the end of preheating stage is a critical premise for balanced filling during production.In the conventional closed-loop control mode,each heater is to be heated up to the desired setpoint as fast as possible.However,such approach may not be the best choice practically.This individual racing to setpoint leads to significant differences among the heating processes during their temperature transition and their setpoint tracking,which may lead to uneven heating of MCHR system.

To overcome the above stated problem,this paper proposes a master–slave generalized predictive synchronization control (MSGPSC)method.Since the widely implemented commercial generalized predictive control(GPC)[19–21]is originally not designed for the synchronization purpose,MS-GPSC extends the commercial GPC by adopting the strategies of‘Master-Slave’and ‘Mr.Slowest’,such that the heating process with the slowest dynamics,so-called‘Mr.Slowest’,is selected as ‘Master’ and tracks the setpoint,while the others are ‘Slaves’ and track the temperature of ‘Master’.This design is expected to synchronize the convergence procedures of heaters to a suitable speed,such that the MCHR system can be sufficiently and evenly heated to the largest extent,while the final convergence to desired setpoint can also be ensured at the same time as commercial GPC does.The issues of parameters tuning and stability are theoretically discussed in this paper,the results of both simulations and experiments show MS-GPSC’s effectiveness on synchronized heat-up.

This rest of paper is organized as follows:section 2 presents the design of proposed MS-GPSC,Section 3 analyses the issues of parameters tuning and stability by equivalent transformation to commercial GPC.The illustrations of simulations and experiments are shown in Sections 4 and 5,verifying the synchronization effectiveness in comparison with commercial GPC.Section 6 concludes.

2.The Design of Master-Slave Generalized Predictive Synchronization Control (MS-GPSC)

2.1.Algorithm formulae

Given that there arenheaters in MCHR system,each heater has its own corresponding temperature sensor.The heating processes in MCHR system could not be precisely modeled in the way of first-principle due to their complicated dynamics nature,and are approximately formulated by following multi-input multi-output(MIMO) CARIMA model:

whereu∊Rn,y∊Rnare inputs and outputs respectively,δ ∊Rnrepresents the uncertainties such as model mismatch,disturbanceetc.tis discrete time spot,z-1is the backward shift operator,Δ is the backward difference operator 1-z-1,dis the process delay,A(z-1)and B(z-1)are the matrix polynomials defined as follows:

Above nominal model (1) with δ=0 is actually obtained by multiplying following ARMAX model by Δ:

whereA0(z-1)=A(z-1)Δ-1,B0(z-1)=B(z-1).Since the coupling effect between heating processes is counted as uncertainty excluded from nominal MIMO model (1) (details can be seen in Appendix),the matrix polynomials Eq.(2) are actually diagonal,which means that the nominal MIMO model (1) actually consistsofnsingle-in single-out (SISO) models,each one represents the standalone nominal model of a heating process,the coupling effect is contained in uncertain term δ.

Fig.2. The comparison of cold runner and hot runner molds,using lens production as example.

In generalized predictive control(GPC)[19–21],nominal model(1) is transformed into following prediction model:

Then based on prediction model (4),the following quadratic convex optimization problem is solve online at each discrete time spottto obtained control lawu(t):

where yr∊Rnis the vector of desired trajectories to be tracked by those heating processes,R and Q ∊Rn×nare the positive definite diagonal weights matrices,N,Nuand diagonal elements of R and Q are parameters to be tuned.Without losing generality,the following theoretical description denotes the 1st heating process as the‘Mr.Slowest’ which is of the slowest dynamics among all heating processes and picked as ‘Master’ process,its desired trajectory is setpointyr0,while its output prediction ^y1is the desired trajectory of the other heating processes,also called ‘Slave’ processes:

Above stated algorithm is called‘Master-Slave’generalized predictive synchronization control (MS-GPSC).

Remark 1.The‘Mr.Slowest’can be selected as the process with the slowest step response,by open-loop step response experiment.Although in real industrial applications with multiple processes operating in parallel,there may not exist a process with persistently slowest dynamics,but in MCHR system,the heating process on manifold is obviously slower than other heating processes due to its large heating area,which can be observed from experiment results shown in Section 5.Thus,the‘Mr.Slowest’strategy is feasible in preheating process control of MCHR system.

2.2.The derivation of explicit control law

For commercial GPC,the desired trajectory is set according to application demands.When it is directly applied on preheating process control of MCHR system,the desired trajectories yrshall be all set as set pointyr0,which makes yra constant vector and leads to easy derivation of explicit control law similar to least minimum square problem.However,the case of MS-GPSC proposed in this paper is more complicated.As indicated by prediction model(4) and desired trajectories setting Eq.(9),the desired trajectories of ‘Slave’ processes is exactly the output prediction ofwhich is the function of Δuto be optimized by Eq.(8) rather than constants,so the method for solving Eq.(8) in case of commercial GPC cannot be directly used in MS-GPSC.This subsection derives the explicit control law of MS-GPSC by using the conclusion of following theorem:

Theorem 1.The quadratic convex optimization problem Eqs.(8),(9)of MS-GPSC can be equivalently transform into following formulation:

where

Fig.3. The product defects caused by imbalanced filing.

Proof:The predictions of tracking errors of‘Slave’processes can be decomposed as:

which leads to:

Then optimization problem Eqs.(8),(9) can be converted as:

Thus theorem 1 is proved.

By using the equivalent quadratic convex optimization problem formulation (10),(11) given by theorem 1,the explicit solution of MS-GPSC can be obtained in the same way as GPC:

Thus,the explicit control law of MS-GPSC is derived without directly solving the quadratic convex optimization problem Eqs.(8),(9),and its difference from commercial GPC lays in matrixwhich is positive definite but not diagonal as indicated by Eqs.(11)and(16),which may lead to differences on parameters tuning and stability from commercial GPC,such issues are discussed in the following section.

3.Parameters Tuning and Stability

There have been a plenty of mature studies on parameters tuning and stability of commercial GPC [22–24].The following theorem presents another equivalent formulation of MS-GPSC to show how to migrate the current results on parameters tuning and stability of commercial GPC to the proposed MS-GPSC.

Theorem 2.The proposed MS-GPSC can also be equivalently presented in following manner:rewrite the controlled MIMO process Eq.(1)as:

and the quadratic convex optimization problem Eqs.(8) and (9) is rewritten as:

Proof:Let the first set of Diophantine Eq.(6) be respectively pre-multiplied by L and post-multiplied by L-1,and the second set of Eq.(6) be only pre-multiplied by L,leading to:

Above Eq.(21) can be further simplified as:

By using the same procedure as commercial GPC,the control law of algorithm Eqs.(17)–(20) is obtained as:

Fig.4. The mechanism of imbalanced filling induced by shearing heat of polymer melt.

By substituting Eqs.(23) and (25) into Eq.(24),it can be easily observed that:

Thus,the control law of algorithm Eqs.(17)-(20) is exactly the sameasMS-GPSCcontrollawEqs.(15)-(16),thetheorem2is proved.

The theorem 2 indicates that the parameters tuning of the proposed MS-GPSC can be done by applying the tuning methods of commercial GPC on equivalent Eqs.(17)-(20).Since the stability of algorithm also relies on the parameters tuning,theorem 2 can also lead to the following corollary:

Corollary 1.The stability of MS-GPSC is equivalent to the stability of commercial GPC on MIMO process Eq.(17).

In summary,the parameters tuning and stability of MS-GPSC can migrate the results of current studies on commercial GPC by mathematical transformation to Eqs.(17)-(20).

Remark 2.>It can be observed that Theorems 1 and 2 represents two equivalent transformations of the proposed MS-GPSC for different purposes:the transformation in Theorem.1 is done from cost function aspect as an easy way to obtain the control law of MS-GPSC,while Theorem.2 transform MS-GPSC from modeling aspect for parameters tuning.The brief schematic illustration on the above stated logical relationship between Theorems1 and 2 is demonstrated as following Fig.5.

Remark 3.The cost function of original commercial GPC based on nominal models(1)-(3)is commonly in following formulae:

Fig.5. Schematic illustration of equivalent transformations in Theorems 1 and 2.

where the desired trajectory of each heating process is set as common setpointyr0.So the tunable parameters of MS-GPSC are common with commercial GPC.However,comparing the equivalent nominal model Eq.(17) of MS-GPSC with that of commercial GPC (1)-(3),it can be seen that the parameters tuning guidelines of commercial GPC and MS-GPSC are different,which makes these 2 algorithms not directly comparable.Thus,as a best compromise for comparison,in the following Sections 4 and 5,the simulations and experiments results are demonstrated to verify that:under the scenario that the setting of common parameters shared by both commercial GPC and proposed MS-GPSC is well-tuned for commercial GPC,the proposed MS-GPSC can achieve the claimed additional synchronization feature by specifically designed cost function structure.

4.Simulations

This section adopts a 6-in 6-out multivariate process with coupling effect for simulation,the process dynamics is as follows:

and the process model used by closed-loop control consists of the following 6 SISO independent dynamics models:

The step responses with of real process(28)and model(29)are shown in Fig.6,indicating that model mismatch between them is quiet obvious,which is suitable for robust stability verification of proposed MS-GPSC.

This paper shows the synchronization property of MS-GPSC by the comparison with commercial GPC.The common settings for both algorithms on parametersyr0,N,Nu,R,Qare adopted,as shown in Eq.(30):

According to the step responses results shown in Fig.6,the‘Master’process is selected as process(5)which is the‘Mr.Slowest’with persistently slowest dynamics.The time span of simulation is 15000,and to make the graphical results more clear,only the first 2000 steps of simulation results of commercial GPC and proposed MS-GPSC are respectively shown in Figs.7 and 8.It can be obviously seen that compared with commercial GPC which achieves satisfactory setpoint tracking performance only,the proposed MS-GPSC not only ensures the convergences to setpoint under existence of uncertainties as commercial GPC,but also achieves the synchronization of 6 processes’ outputs during convergenceprocedure,resulted from the specifically designed equivalent weighted matrix=LTRL in Eq.(11) which makes other ‘Slave’systems take the predicted output of ‘Master’ system as desired trajectory.To verify the synchronization feature of proposed MSGPSC under disturbance,the following abrupt disturbance is added on the right hand side of true process dynamics Eq.(28):

Figs.9 and 10 respectively show the control performances of commercial GPC and proposed MS-GPSC under disturbance Eq.(31).Although at the beginning and the end of disturbed period,the maximum bias of outputs from setpoint in MS-GPSC are slightly larger than in commercial GPC,but MS-GPSC can still ensure the convergence back to setpoint in synchronization mode.In case when the prediction horizon is increased toN=250,the maximum bias is depressed as shown in Fig.11,which is similar to the tuning rules of commercial GPC on prediction horizon.Thus,above simulation results verify the effectiveness of proposed MSGPSC on synchronized setpoint convergence.

5.Experiments

This section demonstrates the experiment verification on the proposed MS-GPSC’s effectiveness.The selected experiment instrument is a MCHR system with 6 parts:1 inlet,1 manifold,4 nozzles,as shown in Fig.12.The temperature of each part is controlled by a solid state relay (SSR) in Fig.13 manipulating a corresponding heating coil,the inputuiis the duty ratio of each SSR(%).The temperature of each part is measured by a J-type thermocouple.

Indicated by the results of step responses experiment under the constant inputui=20 shown in Fig.14,the heating process of manifold is the ‘Mr.Slowest’ to be selected as ‘Master’ process.The settings of common parameters of commercial GPC and proposed MS-GPSC are shown as follows:

Since the duty ratio of SSR can only range from 0-100%,the constraint on inputuiis 0 ≤ui≤100.To tackle this constraint,this paper implements a simple technique commonly used in temperature control of industrial applications: when the inputuicomputed by control law exceeds the bound of constraint range,the value of bound is assigned to the inputuiinstead.The experiment results of commercial GPC and proposed MS-GPSC are respectively shown in Figs.15 and 16.Similar to simulation results,under the scenario that the common parameters setting is suitable for commercial GPC as indicated by the satisfactory tracking performance of commercial GPC in Fig.15,the proposed MS-GPSC achieves the synchronized convergences to setpoint for the temperature of 6 parts.Moreover,the synchronization tendency and high tracking precision are preserved even under noisymeasurement and experimental disturbances,as shown in the scoped view on steady state in Fig.17,and the control inputs changing amplitudes of MS-GPSC shown in Fig.16 appear to be larger than those of commercial GPC shown in Fig.15 as the result of MS-GPSC’s effort on synchronization maintenance under stochastic disturbance,which also verifies the synchronization performance in Fig.17 from another angle.

Fig.6. The step responses of real process (28) and model (29).

Fig.8. The simulation results of proposed MS-GPSC.

Fig.9. The simulation results of commercial GPC under disturbance.

Fig.10. The simulation results of proposed MS-GPSC under disturbance.

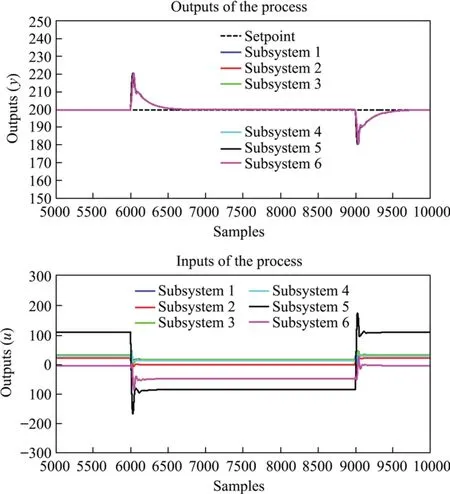
Fig.11. The simulation results of proposed MS-GPSC under disturbance with N=250.

Fig.12. The multi-cavity hot runner system used in experiments.

Fig.13. The solid state relays used in experiments.

Fig.14. The step responses of heating processes.

6.Conclusions

Corresponding to the demands for even temperature distribution of multi-cavity hot runner (MCHR) system in injection molding,this paper proposes a master–slave generalized predictive control with Mr.Slowest strategy (MS-GPSC).By synchronizing the heat-up procedures of all heating processes of the MCHR,the more sufficient and even heating can be expected during the preheating stage.The parameters tuning guideline is practically clear from theoretical aspect,and the effectiveness is proved by both simulations and experiments.

The future works can be carried on in two-fold:

(1) The proposed MS-GPSC is constraint-free during its derivation and analysis,but in the experiment,there exists the input constraint due to physical property of MCHR system.The method to tackle this input constraint in this paper is a commonly used practical mean in industry.To handle more general constraint problem,which may be encountered while implementing MS-GPSC,from theoretical aspect,many mature researches on constraint problem of model predictive control (MPC) can be migrated to MS-GPSC inthe future works since the input constraint does not influence the conclusions of Theorems 1 and 2 which only concern about cost function and process model.

Fig.15. The experiment results of commercial GPC.

Fig.16. The experiment results of proposed MS-GPSC.

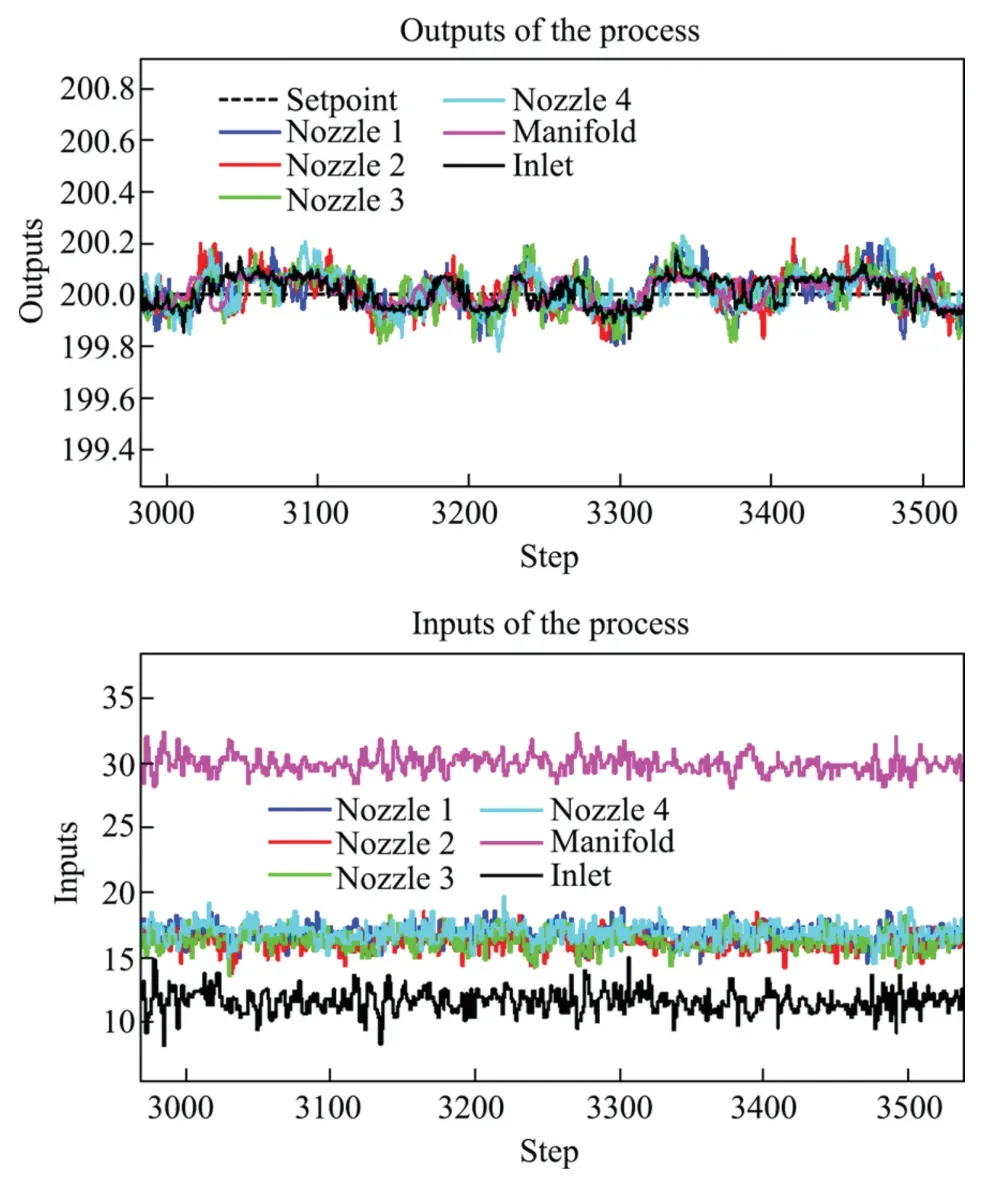
Fig.17. The scoped view of experiment results of proposed MS-GPSC at steady state.

(2) The proposed MS-GPSC is based on the default assumption that the temperature states of the sparsely distributed thermocouples can represent the temperature state of the whole MCHR system.However,the actual temperature state of the whole MCHR is practically unobservable.Thus,in the future works,more extensive studies such as finite element analysis can be conducted to further optimize the preheating strategy.

Appendix.Uncertainty on Coupling effect

The true dynamics of MIMO heating processes in the MCHR system can also be represented by the following NARMAX (nonlinear auto regressive moving average with exogenous input) model:

where fNARMAXis bounded nonlinear function vector.Above equation means that the dynamics of each heating process can be written as:

It is worth to be noticed that the full-length vector y and u infNARMAX,jhave contained the coupling effect between heating processes.Rewrite the MIMO CARIMA model used in our paper as follows:

with diagonal A(z-1)and B(z-1),which means that the dynamics of each heating process can be specified as:

Combine the above 2 models,the detailed formulae of δt() can be obtained as:

which contains the coupling effect between heating processes asfNARMAX,jdoes.SincefNARMAXis bounded.Thus,the coupling effect between heating processes can be modelled as bounded uncertain terms.

Data Availability

The authors do not have permission to share data.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This project is supported in part by National Natural Science Foundation of China(62203127),Basic and Applied Basic Research Project of Guangzhou City (2023A04J1712),The Foshan-HKUST Projects Program (FSUST19-FYTRI01) and GDAS’ Project of Science and Technology Development (2020GDASYL-20200202001).