Effects of channel wall wettability on gas–liquid dynamics mass transfer under Taylor flow in a serpentine microchannel

Xuancheng Liu,Hongye Li,Yibing Song,Nan Jin,Qingqiang Wang,Xunli Zhang,Yuchao Zhao,

1 Shandong Engineering Research Center of Green Manufacturing for New Chemical Materials, College of Chemistry &Chemical Engineering, Yantai University, Yantai 264005, China

2 School of Engineering & Institute for Life Sciences, University of Southampton, Southampton SO17 1BJ, UK

Keywords:Microreactor Microchannels Mass transfer Wettability Taylor flow Gas–liquid two-phase

ABSTRACT The wall wettability of microchannels plays an important role in the gas–liquid mass transfer dynamics under Taylor flow.In this study,we regulated the contact angle of the wall surface through surface chemical grafting polymerization under controlled experimental conditions.The dynamic changes of CO2 bubbles flowing along the microchannel were captured by a high-speed video camera mounted on a stereo microscope,whilst a unit cell model was employed to theoretically investigate the gas–liquid mass transfer dynamics.We quantitatively characterized the effects of wall wettability,specifically the contact angle,on the formation mechanism of gas bubbles and mass transfer process experimentally.The results revealed that the gas bubble velocity,the overall volumetric liquid phase mass transfer coefficients(kLa),and the specific interfacial area (a) all increased with the increase of the contact angle.Conversely,gas bubble length and leakage flow decreased.Furthermore,we proposed a new modified model to predict the gas–liquid two-phase mass transfer performance,based on van Baten’s and Yao’s models.Our proposed model was observed to agree reasonably well with experimental observations.

1.Introduction

In recent decades,multiphase systems involving gas and liquid phases in microchannel reactors have demonstrated precise controllability of flow hydrodynamics,narrow feed residence time distribution,specific temperature profile,and enhanced mass transfer compared to conventional systems [1–4].Additionally,these microreactors have shown improvements in terms of selectivity and reproducibility of multiphase reactions,energy and raw material utilization efficiency,process control,and operational safety,largely owing to their microscale characteristic dimensions,larger surface-to-volume ratios,and shorter mass transport distances.As a result,extensive research has been conducted to characterize these systems,with a particular focus on gas–liquid two-phase flow hydrodynamics and mass transfer in various microchannels[5–11],which are considerably different from conventional macroscale systems.Fundamentally,the surface tension and viscous forces in microchannels become predominant compared to gravitational or inertial forces,thereby determining gas–liquid twophase flow patterns and the performance of mass transfer.

One of the predominant and widely used flow regimes for gas–liquid two-phase flow in microchannels is Taylor flow or slug flow,which is typically characterized by the presence of elongated gas bubbles (dispersed phase) with a length longer than the channel diameter or width.As these gas bubbles flow along the microchannel,they are separated from each other by liquid slugs(continuous phase).In Taylor flow,the typical gas–liquid two-phase interfacial mass transfer process takes place across the interface from the gas bubble to the liquid bulk slug,from the gas bubble to the liquid film,and between the gas bubble and the wall.The mixing or mass transfer between the liquid film and the liquid bulk slug can be further performed by the leakage flow in the liquid film and the internal circulation in the liquid bulk slug,along with molecular diffusion [12,13].Therefore,the interfacial area,the velocity of the leakage flow,and the internal circulation considerably determine the surface renewal rate and the mass transfer rate.Additionally,the gas–liquid interface generally deforms during the motion of the liquid slugs and the gas bubbles,which can affect the velocity profile and the internal circulation in the liquid slugs,thereby the mass transfer efficiency [14,15].

It is well established that the flow hydrodynamics in Taylor flow are affected by surface wettability [16–19],which is quantified in terms of contact angle.Cubaudet al.[17]carried out experimental investigations on the shape of static and moving elongated bubbles in glass/silicon microchannels coated with Teflon to alter the wall surface contact angle that,which changed the flow regime.Santos and Kawaji [18] examined the effect of contact angle on slug formation in a T-junction microchannel using 3D numerical simulation.They found that the gas–liquid interface shape changed from concave to convex on the liquid side as the contact angle increased.A completely hydrophilic channel was observed to have greater velocity gradients within the gas bubbles,inducing more internal mixing.Moreover,hydrophilic walls retained near-stagnant liquid around the channel corners,contributing to the occurrence of velocity slip.Wielhorskiet al.[20]experimentally studied the effect of liquid–solid contact angle on the formation processes and length of gas bubbles under different wetting situations,using various liquids as the continuous phase.The results showed discrepancies between the measured gas bubble lengths for partial or non-wetting issues and those predicted by Garstecki’s model for completely wetting systems [3].Zhouet al.[21]observed through numerical simulation that the contact angle had a great influence on the flow regimes,transition lines,and bubble length.In the wetting systems,both the slug flow region and the gas bubbles length increased with increasing contact angle,which agreed with the modeling results of Qian and Lawal [22].Srinivasan and Khandekar [14] quantitatively revealed the local flow characteristics and velocity field behind the meniscus in a hydrophilic microchannel.They found that the liquid bulk slug(far from meniscus) followed a parabolic profile,while approaching the meniscus,it became flatter and formed a double vortex,leading to an enhancement of local mass transfer.

The study of mass transfer in gas–liquid Taylor flow in microchannels has been extensive,involving both numerical and experimental methods.Various mass transfer mechanisms and empirical or semi-empirical correlations have been proposed.Bercˇicˇand Pintar[23]conducted experiments to measure the overall volumetric mass transfer coefficients (kLa) of methane absorption in water during slug flow in three sizes of hydrophilic glass capillaries.They proposed a semi-theoretical model based on a unit cell model,which only considered the mass transfer contribution from the bubble caps,resulting in an underestimation ofkLafor the methane–water system.To account for the contribution of the liquid film and the bubble caps,Van Baten and Krishna[24]developed a model based on a circular channel.However,this model tended to overestimatekLavalues due to the assumption of a uniform liquid film thickness along the capillary,which is not suitable for square or rectangular microchannels with thicker liquid films in the corners.Vanduet al.[25] proposed a simplified model,assuming that the dominant mass transfer contribution comes from the liquid film for extreme short gas–liquid contact times.Their experimental results for an air–water system were in agreement with this model.

The dynamics of gas–liquid mass transfer in microchannels have been studied to address the limitation of the aforementioned models,which assumed constantkLavalues along the microchannels.However,such models are not suitable for describing processes involving quick dissolution or high solubility of gases in absorbents,wherekLavalues change rapidly due to the variation of bubble volume along the microchannel.To overcome this limitation,Abolhasaniet al.[26] conducted experiments on a siliconbased microfluidic platform to investigate the evolution of gas bubbles for CO2–water and dimethyl carbonate systems,obtaining a series ofkLavalues based on bubble shrinkage.Tanet al.[8]proposed a semi-empirical correlation based on a similar method and their experimental data,which was helpful in predictingkLavalues.Yaoet al.[27] improved the unit cell model and investigated mass transfer by measuring the absorption rate of CO2–water system.To quantify the dynamic change of mass transfer,Zhanget al.[28] calculated the transient change value ofkLaduring the gas–liquid mass transfer process of CO2in water.Their results showed thatkLagradually decreased along the microchannel.Panget al.[29] suggested that mass transfer of CO2bubbles in serpentine microchannels should include a fast dissolution zone and a slow dissolution zone,wherekLaincreased with the increase of the leakage flow in the liquid films between the bubbles and the channel walls.

Recently,numerous advanced experimental methods have been proposed to investigate gas–liquid mass transfer based on gas physical absorption.Deleauet al.[30,31] experimentally determined the local volumetric mass transfer coefficients along the silica capillary for a high-pressure CO2–water system using Raman spectroscopy and a colorimetric method.Meiet al.[32,33] used a resazurin-based colorimetric technique and image processing to investigate gas–liquid mass transfer around Taylor bubbles,wherekLawere evaluated based on those coloration positions.They found that two highly concentrated oxygen concentration spots were formed near the bubble rear and the channel wall region,and a much more complex flow structure in the liquid slug appeared.All investigations mentioned above demonstrated that the flow hydrodynamics in the liquid film and the liquid bulk slug played a significant role in gas–liquid mass transfer processes.However,these reported correlations for estimating of mass transfer coefficients did not consider the effect of wall surface wettability,which can significantly affect the flow hydrodynamics,especially in the liquid film,and necessitates further investigation.Ultimately,gaining insights into the effect of wall surface wettability in microchannels can assist the material selection and operation of microchannel reactors.

The aim of this study was to quantitatively characterize the effect of microchannel wall surface wettability on multiphase mass transfer dynamics by varying static contact angle.To achieve this,three different degrees of static contact angles at 10°,40° and 70°were examined using a plasma-induced graft polymerization technology,where the methylacryloethyl sulfonyl betaine(SBMA) was grafted onto the surface of polymethyl methacrylate (PMMA).The study focused on the effects of wettability on the formation of gas bubbles and liquid slugs,as well as the length and velocity of gas bubbles.To better understand the gas–liquid two-phase dynamics and mass transfer characteristics,a semi-empirical correlation based on a unit cell model was proposed to quantify the effect of wettability on gas–liquid mass transfer dynamics in Taylor flow.

2.Experimental

Fig.1 shows a schematic of the experimental setup,previously described in our work [4,28].The setup consisted of microchannel chips,fluid conveying devices,and an image acquisition system.The microchannel chip had a width and depth of 600 μm and 300 μm,respectively,in the gas absorption zone and pressure buffer of the gas phase.The size of the pressure relief zone near the outlet was 1.0 mm × 1.0 mm.Pure CO2(99.999%) and deionized water were used as working fluids.Liquid flow rate was calibrated using a weighting method,and a microsyringe pump(Harvard PHD 2000,USA) with a stainless-steel syringe (0–50 ml,Longer,China)was used to deliver deionized water.A high pressure microsyringe pump (LSP01-1BH,Longer,China) with a stainless-steel syringe was employed to convey pure CO2,calibrating using an automated electronic soap film flowmeter (GL-101B,0.1–100 ml∙min-1,accuracy 1%,Beijing Beifen Sanpu,China).To ensure stable gas flow rates,a back pressure valve was installed between the microsyringe pump and a check valve.Gas and liquid flow rates were set in the range of 2.5–4.5 ml∙min-1and 1.0–2.5 ml∙min-1,respectively,to obtain a stable Taylor flow along the microchannel.The superficial Reynolds numbers of gas and liquid phase were controlled in the range of 2.17–3.90 and 27.64–69.10,respectively,to maintain stable Taylor flow.Operating temperature was controlled at 25 °C.Dynamic changes of CO2bubbles along the microchannel were monitored using a high-speed video camera(R311,Phantom,USA;3200 frames per second) mounted on a stereo microscope(SZX 16,Olympus,USA).The resolution and exposure time were set at 1280 pixel × 800 pixel and 490 μs,respectively.When the formation frequency and length of gas bubble reached a stable state,image acquisition began,with 1000 images captured for each run,which was repeated at least three times.Finally,all pictures were processed by Matlab image analysis program,and relevant parameters of Taylor flow (length and velocity) were obtained.

Fig.1. Schematic diagram of the experimental setup.

Microchannel chips with long serpentine square microchannels were fabricated on PMMA plates(A grade,92%light transmittance,ShenZhen HuiLi Acrylic Products Co.,Ltd.,China) using precision milling technology.The chips were then cleaned alternately with ethanol (1–2 min) and deionized water in an ultrasound equipment.After drying with nitrogen,the machined PMMA plate was exposed to air plasma for 3.0 min.During the plasma process,accelerated electrons bombarded on microchannel walls,breaking down the molecular bonds(C—C and C—H,etc.)and producing free radicals that reacted with O2to form carboxylic and hydroxyl groups.The microchannel was then treated with a degassed SBMA aqueous solution(0.3 mol∙L–1)and exposed to UV irradiation for 5–20 min to induce surface chemical grafting polymerization.The wettability of microchannel wall was regulated by varying the exposure time.Unreacted SBMA was eliminated by cleaning with deionized water in an ultrasound equipment.The static contact angle of deionized water on modified PMMA substrate of dimensions 20 mm×20 mm was measured(see Fig.2).To ensure uniformity,tens of microchannel chips were machined,and dozens of microchannel chips before surface modification were selected based on similar gas–liquid two-phase flow characteristics.Compared to circular capillaries,measuring the advancing and receding contact angles in square/rectangle hydrophilic microchannels is more difficult.Thus,the static contact angle of the wall surface was chosen as the indicator of surface wettability in this work to avoid the effects of surface roughness and non-uniformity.

3.Mass Transfer Analysis Based on Unit Cell Model

The unit cell model has frequently been employed to analyze the gas–liquid mass transfer characteristics under Taylor flow[4,24,27,28,30],as shown in Fig.3.For the CO2–H2O two-phase system,a unit cell consisted of one CO2bubble (Taylor bubble),one liquid slug(H2O),and a liquid film surrounding the bubble and slug due to the hydrophilic wall in this study.This model simplified the gas–liquid two-phase mass transfer of Taylor flow based on several assumptions: (i) gas and liquid phases were well-mixed within each unit cell;(ii) the overall unit cell was treated as a plug flow reactor;(iii)there was no mass transfer between the adjacent unit cells;(iv) gas–liquid two-phase mass transfer occurred only in a single unit cell;(v)both the amount of H2O in CO2and the physical properties of liquid phase were negligible.

Based on the above assumptions,the mass balance of CO2in a unit cell was written as the following.

whereVB,UB,kL,a,VBandall are functions of position(z),which varies along the serpentine microchannel.PBis gas phase pressure,which is considered as linear relation with the position due to very low pressure drop in our experiments,Pa.Ris gas constant,8.3145 J∙mol-1·K-1.Tis operating temperature,K.VBis CO2bubble volume,m3.UBis bubble velocity,m∙s-1.zis position along the serpentine microchannel,m.kLis liquid phase mass transfer coefficient,m∙s-1.ais specific interfacial area (a=AS/(VCO2+VL)),m-1.ASis effective mass transfer area,m2.VLis liquid phase volume including the liquid slug and the liquid film,m3.is CO2concentration in liquid phase,mol∙m-3.is saturated solubility of CO2in pure water,mol∙m-3,which is estimated by empirical correlation based on Henry’s Law [34].

Fig.2. Three microchannels with different static water contact angles.

Fig.3. Schematic of a typical gas–liquid mass transfer unit cell in Taylor flow along a microchannel.

The gas bubble shape assumption in our previous work to estimate ofVBwas still employed [4,13,28],with two bubble caps being considered as hemisphere.Under our operating conditions,the gas bubble length(LB),microchannel width,and film thickness(δ) fall in the range of 5.0–8.0,0.6,and～0.006 mm,respectively.Hence,the film thickness can be neglected in comparison to the gas bubble length,and the gas bubble volume can be expressed by Eq.(2).All experimental data from the images are based on pixels with a specific size determined by the microchannel width.During the experiments,the location or changes of the microchannel chips may affect the measurement accuracy.Therefore,the accuracy of gas bubble length (LB) and the radius of the quadrant at the corner (r) is between 2%–5% and 5%–8%,respectively.

whereris the radius of the quadrant at the corner,m.wandLBare the channel width and gas bubble length,respectively,m.δwallis the liquid film thickness near the channel wall center and estimated by Aussillous and Quéré’s correlation [35].

where μLis liquid phase viscosity,Pa·s.γLis gas–liquid interfacial tension,N∙m-1.LB,UBandrare obtained from 1000 continuously captured images by Matlab image analysis program.VBalong the microchannel is calculated by Eq.(2)and then dVB/dz.VLis deduced from the formation frequency of the liquid slug.Finally,kLaalong the serpentine microchannel is calculated by Eq.(1).

4.Results and Discussion

4.1.Effect of channel wall wettability on gas bubble length and velocity

Gas bubble length is a key parameter in determining flow hydrodynamics,mass transfer,and reaction in the gas–liquid two-phase system along microchannels.The bubble size is influenced by channel geometry,fluid properties,surface characteristics,and operating conditions [3,13,36].In this study,we focused on investigating the impact of surface wettability on the evolution of CO2bubbles along the serpentine microchannel,as shown in Fig.4.Our results indicate that an increase in the contact angle or gas phase flow rate,or a decrease in the flow rate of liquid phase leads to a reduction in the gas bubble length.Additional experimental data are presented in Supplementary Material.The initial gas bubble length was found to be dependent on the formation characteristics of gas bubbles at the T-junction for different contact angles,as illustrated in Fig.5.

The bubble formation process during one cycle consisted of three distinct steps,namely,moderate expansion,slow squeezing,and fast rupture.The expansion times during the moderate expansion step were 6.25,4.69,and 2.19 ms for contact angle degrees of 10°,40° and 70°,respectively.During their corresponding expansion times,Taylor bubbles formed in the previous circle moved downstream about 1.00,0.92,and 0.50 mm,respectively,with moving velocities of 0.16,0.20,and 0.23 m∙s-1,respectively.

Under the same operating conditions,the liquid phase flowed downstream more easily from the four corners and thin liquid film between the gas bubble and the channel wall due to the increased wettability.This intensified the leakage flow and decreased both the transient pressure at the T-junction and the apparent driving force for moving downstream in CH-I,which,in turn,reduced the moving velocity of the gas bubble.After the rupture of gas bubble in the previous circle,a new gas–liquid interface was formed at the T-junction.This interface was bound to retract into the gas phase inlet channel and tend to minimize the gas–liquid twophase interface under surface tension.During the retraction of gas–liquid interface,the gas–solid interface was inevitably replaced by the liquid–solid interface,accompanied by a Gibbs free energy change(-ΔG=γSG-γSL=γLGcosθ),denoting a larger Gibbs free energy change in CH-III.The retraction distance decreased,and a part of the new bubble nose would remain in the main microchannel,resulting in a decrease of the expansion time,as shown in Fig.5.

During the slow squeezing step,the squeezing times in CH-I,CH-II and CH-III were 34.38,26.25 and 20.62 ms,respectively.Since the main microchannel was obstructed by the gas bubble nose,the pressure difference across the gas–liquid interface increased [3],causing leakage flow [13].While the former factor facilitated the movement of the gas bubble nose downstream and a decrease in the gas phase neck width near the T-junction,the latter had an opposite effect.Compared to CH-II and CH-III,the stronger wettability in CH-I intensified the leakage flow and reduced the pressure difference under the same operating condition.Typically,the squeezing time was determined by the interplay of these two competitive factors.However,during squeezing the gas phase neck in CH-I,the contribution of the pressure difference to gas bubble length dominated over the shear stress caused by the leakage flow under this operating condition.

Fig.4. Evolutions of gas bubble length along the microchannel at 25 °C and 0.1 MPa for (a) QG=3.5 ml∙min-1, QL=1.0 ml∙min-1;(b) QG=4.5 ml∙min-1, QL=2.0 ml∙min-1.

Fig.5. Bubble formations at QG=3.5 ml∙min-1, QL=1.0 ml∙min-1 for different contact angles.

From the experimental data presented in Fig.5,it can also be observed that the squeezing time increases as the contact angle decreases,which favours the increase in gas bubble length.This is accordance with the squeezing mechanism where the pressure difference is mainly responsible for squeezing the emerging gas bubble [3].In the fast rupture step,it is interesting to note that the rupture times are all about 0.31 ms for all three contact angles.This suggests that the combined effects of the leakage flow and pressure difference on the gas phase neck were nearly equivalent in CH-I,CH-II,and CH-III.Based on the above discussion,the leakage flow gradually decreases as gas bubble length increases due to the increase in flow resistance during the squeezing step.At the same time,the pressure difference across gas–liquid interface in the vicinity of the T-junction also increased correspondingly.As the leakage flow levels off,it signals the start of the fast rupture step and the ending of the squeezing step for each contact angle.Fig.6 illustrates the gas bubble shrinkage evolution along the microchannel with an increasing contact angle.The gas bubble decrease process consisted of three stages: fast linear decreasing stage (R2>0.99),moderate exponential decreasing stage(R2>0.99),and slow linear decreasing stage(R2>0.99).At a given gas and liquid phase flow rate (Fig.4(a)),the initial gas bubble length decreased from 5.67 to 4.35 mm as the contact angle increased from 10°to 70°.To characterize the variation of gas bubbles with different contact angles,we defined a relative gas bubble length shrinkage rate.

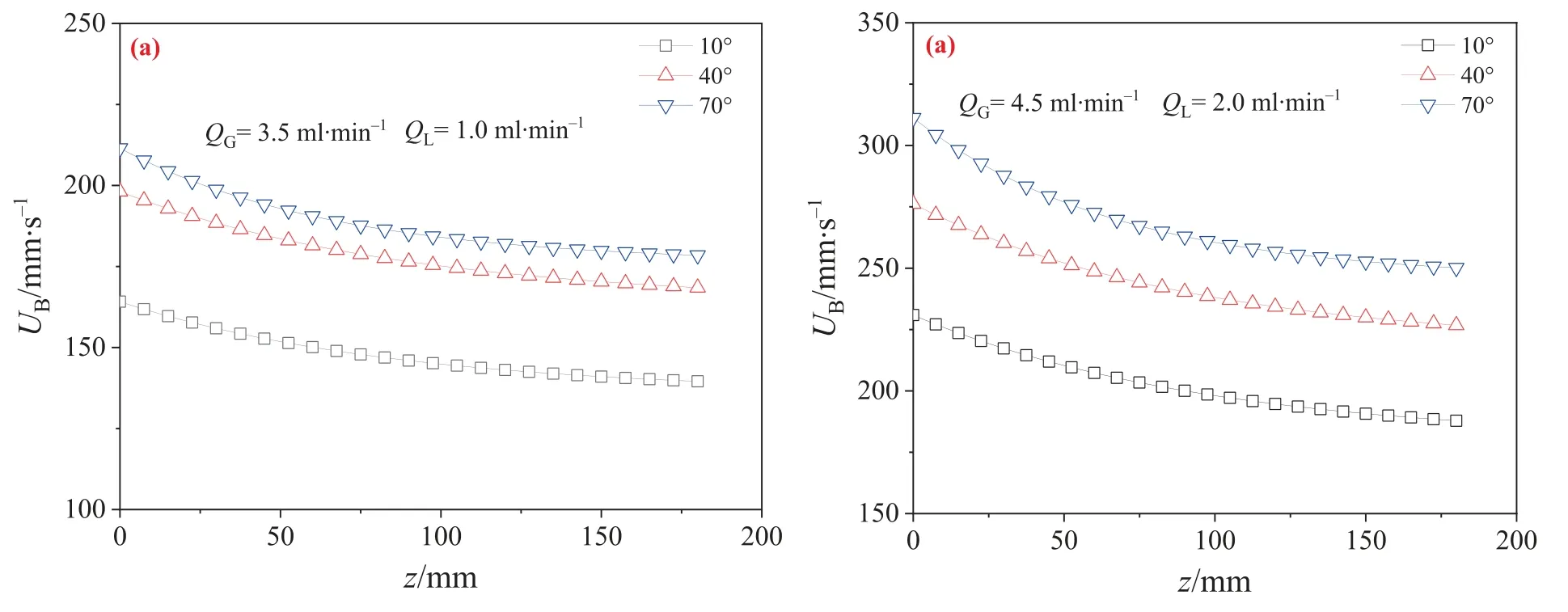
whereLB,0,LB,zandLB,180,denote the gas bubble length at initial position (z=0 mm),at a certain position (0 mm

In the fast linear decreasing stage(z≤20 mm),the relative gas bubble length shrinkage rate were 0%–19.40%,0%–23.05%and 0%–27.52% for the contact angles of 10°,40° and 70°,respectively.These experimental data indicate that a larger contact angle is more beneficial to the decrease in gas bubble length.This is attributed to the interplay between CO2dissolution in the liquid phase and gas–liquid two-phase pressure drop[28].Compared to the former,the effect of local pressure is more complex.According to Fuerstman’s model[37],the total pressure drop in a unit cell(ΔPto-tal) originates from the region of one gas bubble body,the liquid slug,and two caps of the gas bubble.The pressure drop across the length of the gas bubble body (ΔPbody) is proportional to the leakage flow and the length of the gas bubble body.The wettability on the channel surface increases with a decrease in the contact angle,so both the leakage flow and the length of gas bubble body increase,as validated by experiments for the Ar–H2O system in the later section (Fig.7).

Fig.6. Evolutions of gas bubble shrinkage along the microchannel at 25°C and 0.1 MPa for(a)QG=3.5 ml∙min-1,QL=1.0 ml∙min-1;(b)QG=4.5 ml∙min-1,QL=2.0 ml∙min-1.

Under the same operating condition,ΔPbodydecreased as the contact angle increased.The pressure drop across the liquid slug(ΔPslug) was proportional to the velocity and length.The velocity of the liquid slug was strongly influenced by the velocity of the gas bubble,which increased with the contact angle (Fig.8).Since the length of the liquid slug was proportional to the expansion time,it decreased as the contact angle increased.Therefore,the variation of ΔPslugwas complex and depended not only on the contact angle,but also on the specific operating condition.Additionally,as Fig.5 shows,the difference in liquid slug length was almost negligible under the operating conditions.

Furthermore,under the operating conditions,ΔPslugincreased with the increasing contact angle.The pressure drop across two caps of the gas bubble (ΔPcaps),which was proportional to 2/3 power of the velocity of the liquid slug,also increased with the increase of the contact angle [37].Compared to ΔPslugand ΔPcaps,ΔPbodycould be neglected,as previously reported [37].Therefore,ΔPtotalincreased with the increase of the contact angle under the operating conditions,leading to the rapid shrinkage of the gas bubble.Meanwhile,as the local pressure increased,both the saturated solubility and the CO2dissolution rate gradually increased,further accelerating the shrinkage of the gas bubble.

In the moderate exponential decreasing stage (20 mm

Fig.8 depicts the effect of the contact angle on the velocity of the gas bubble flowing along the microchannel.It was observed that the gas bubble velocity increased with an increase in the contact angle.The initial gas bubble velocity increased from 164.1 mm∙s-1at 10°to 211.5 mm∙s-1at 70°,primarily due to variations in leakage flow and gas bubble length.To clarify the mechanism,an Ar–H2O system without any gas absorption was chosen as the working fluid.The definitions and computational method for the leakage flow were adopted from previous work[38].A unit cell consisted of a liquid slug and a gas bubble,with the leakage flow equal to the difference between the total flow rate of the gas–liquid two phases and the formation rate of the unit cell based on the gas bubble generation frequency.

Fig.7. Bubble formations at QG=3.5 ml∙min-1, QL=1.0 ml∙min-1 for Ar–H2O system with different channel surface contact angles.

Fig.8. Evolutions of gas bubble velocity along the microchannel at 25°C and 0.1 MPa for(a)QG=3.5 ml∙min-1,QL=1.0 ml∙min-1;(b)QG=4.5 ml∙min-1,QL=2.0 ml∙min-1.

whereQleak,QGandQLare the leakage flow,the gas and liquid phase flow rates,ml∙min-1,respectively.fis the gas bubble generation frequency,which was calculated as the gas bubbles number divided by the time duration.

The experimental results showed that the leakage flow decreased as the contact angle increased,with values of 0.63 ml∙min-1for 10°,0.37 ml∙min-1for 40° and 0.17 ml∙min-1for 70° under the conditions ofQG=3.5 ml∙min-1andQL=1.0 ml∙min-1.At the same time,as seen from Fig.7,the gas bubble length decreased from 5.30 to 4.05 mm.On the one hand,an increase in wall wettability reduced flow resistance and further promoted the leakage flow.Moreover,longer gas bubble formation times caused more liquid to flow downstream through four corners and the liquid film,further increasing the leakage flow.On the other hand,the long gas bubble increased flow resistance in the four corners and the liquid film,which had a tendency to decrease the leakage flow and slow down the gas bubble velocity.However,the final experimental results showed that the negative effect of the gas bubble length on the leakage flow was compensated by the increase in wall wettability and the long formation time of the gas bubble.Within a unit cell,an increase in the leakage flow led to a decrease in the upstream pressure of the gas bubble,which in turn reduced the driving force pushing gas bubble to move downstream,thereby decreasing the gas bubble velocity.

4.2.Effect of wettability on mass transfer

The effects of the contact angle on the overall volumetric liquid phase mass transfer coefficients (kLa),the specific interfacial area(a),and the liquid phase mass transfer coefficient (kL) were illustrated in Figs.9–11,respectively.It can be seen thatkLa,a,andkLincrease with the increase of the contact angle.The variation ofkLagradually decreases along the microchannel accompanied by CO2absorption in water,especially inz<100 mm zone.In a unit cell,the mass transfer for Taylor flow mainly consists of CO2transfer from two end-caps to the liquid bulk slug (kL,capacap) and from gas bubble body to its surrounding liquid film(kL,filmafilm).Our previous work demonstrated that the mass transfer in the liquid film was far from being saturated [28],where the overall gas–liquid interface area contributed to mass transfer.Under identical operating conditions (e.g.,QG=3.5 ml∙min-1andQL=1.0 ml∙min-1),the decrease of the gas bubble length implied that the dispersity of gas phase and the gas–liquid specific interfacial area increased(Fig.10),resulting in the increase ofacapandafilm.Meanwhile,both the liquid film length and the frequency of the liquid slug reduced with the increase of the contact angle,which had a tendency to promote the leakage flow.On the contrary,the leakage flow actually decreased because of the increase in the contact angle,which weakened the mixing between the liquid bulk slug and the liquid film,as well as the liquid mass transfer coefficients (kL,capandkL,-film).The increase of the gas bubble velocity in the microchannel with a large contact angle resulted in the increase of the relative movement between the gas bubble and the continuous liquid phase (the liquid film and the liquid bulk slug),intensifying the convective mixing in the vicinity of two caps and in the liquid film,as well askL,capandkL,film.Based on the experimental results,it can be concluded that the positive effects on the mass transfer performance originating from the contact angle under identical operating conditions dominate over their corresponding negative effects,as shown in Fig.11.

4.3.Comparison with other model from literature

Fig.12 presents a comparison between experimentally measured dynamickLavalues and predicted values based on classic models from literatures for gas–liquid Taylor flow along a microchannel under two typical sets of operational conditions with three different channel surface contact angles.The figure includes data from two improved mass transfer models proposed in literature based on the mixing performance between the liquid bulk slug and the liquid film,namely the van Baten model [24] and the revised van Baten model by Yaoet al.[39].The van Baten model[24,40] is based on the key hypothesis of ideal mixing in the continuous phase,which is difficult to obtain.Based on Higbie’s penetration mass transfer theory,the model derives the following equations,although the assumption of constant gas bubble length andkLaalong the channels in and overestimated predictedkLavalues,as shown in Fig.11.

Fig.9. Evolutions of kLa along the microchannel as a function of contact angle at 25 °C and 0.1 MPa for (a) QG=3.5 ml∙min-1, QL=1.0 ml∙min-1;(b) QG=4.5 ml∙min-1,QL=2.0 ml∙min-1.

Fig.10. Evolutions of a along the microchannel as a function of contact angle at 25 °C and 0.1 MPa for (a) QG=3.5 ml∙min-1, QL=1.0 ml∙min-1;(b) QG=4.5 ml∙min-1,QL=2.0 ml∙min-1.

Fig.11. Evolutions of kL along the microchannel as a function of contact angle at 25 °C and 0.1 MPa for (a) QG=3.5 ml∙min-1, QL=1.0 ml∙min-1;(b) QG=4.5 ml∙min-1,QL=2.0 ml∙min-1.

Fig.12. Comparison of experimental with predicted kLa by different models.

Yaoet al.[39] introduced Capillary number (Ca) and the length ratio of gas bubble to liquid slug into the semi-theoretical model(Eq.(9)),considering the local concentration distribution in the liquid bulk slug and the liquid film.Additional terms were adopted to describe the local mixing efficiency in the continuous phase.Compared to van Baten’s model,both the predictedkLavalues and deviation from the experimental values decreased.

In this study,a new model was proposed by further considering the effects of nonideal mixing and contact angle.The physical absorption equilibrium between the transient and saturated gas bubble velocity was used to calculatekL,capacapandkL,filmafilmin Eqs.(6)and (7).The experimental results showed that the surface wettability had a significant impact on the local mixing of liquid slugs,and thus,Capillary number was inserted into the termskL,capacapandkL,filmafilmto fit the experimental data,as described in Eq.(10) using non-linear regression analysis.The predictedkLavalues using the proposed semi-empirical correlation were found to be closer to the actual experimental data than other classic mass transfer models.These empirical data indicated that the effects of operating conditions and surface wettability on the mixing performance in the bulk slug and between bulk slug and the film.For CO2–H2O system,the proposed correlation could partly reflect the effect of contact angle on the dynamic mass transfer performance along the mirochannel.However,for a more precise theoretical model,further investigation is required by optimizing the geometry and surface characteristics of microchannel reactors,which is under active investigation in our laboratories.

5.Conclusions

Gas–liquid two-phase microchannel reactors are influenced by various factors such as channel geometry,fluid properties,surface characteristics,and operating conditions which are all crucial for flow hydrodynamics,mass transfer,and reaction.In this study,the effects of channel wall surface wettability on gas–liquid mass transfer dynamics was examined by tracking the evolution of CO2bubbles in a serpentine microchannel.

To regulate the surface wettability in terms of contact angle of microchannel wall,we used air plasma treatment and surface chemical grafting polymerization under UV irradiation.We captured the dynamic changes of CO2bubbles along the microchannel using a high-speed video camera mounted on a stereo microscope.A unit cell model was introduced to investigate gas–liquid dynamic mass transfer under Taylor flow.It was concluded from the experimental data that the effects of surface wettability were important.The differences of the formation mechanism of gas bubble were observed at the T-junction for different contact angles.Gas bubble length decreased with an increase in the contact angle under identical operating conditions,as well as an increase in gas phase flow rate or with reducing liquid phase flow rate.This was attributed to large leakage flow from the four corners and thin liquid film between the gas bubble and the channel wall due to the increase in the wettability.A relative gas bubble length shrinkage rate was defined for studying the variation characteristics of gas bubbles with the contact angle.The process of gas bubble shrinkage could be divided into three stages,i.e.,fast linear decreasing stage,moderate exponential decreasing stage,and slow linear decreasing stage.The large contact angle was beneficial to the decrease of gas bubble length.It was also observed that the gas bubble velocity increased with the increase of the contact angle,where the negative effect of the gas bubble length on the leakage flow was compensated by the increase of the wall wettability and the long formation time of the gas bubble.The overall volumetric liquid phase mass transfer coefficients (kLa) and the specific interfacial area (a) increased with the increase of the contact angle,where the positive effect on the mass transfer performance originated from the contact angle under the identical operating conditions dominated over theirs corresponding negative effects.Finally,for predicting the gas–liquid two-phase mass transfer performance a new model was proposed by considering the effects of the contact angle and the non-ideal mixing in the continuous phase.

Data Availability

Data will be made available on request.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

We gratefully acknowledge the financial supports from National Natural Science Foundation of China (21978250,22208278) and Natural Science Foundation of Shandong Province(ZR2020KB013,ZR2020QE211,2019KJC012).

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.cjche.2023.04.006.