带有泡沫与崩盘的可预测模型检验①

2023-12-30 06:11杨炳铎杨子晖陈海强

管理科学学报 2023年9期

杨炳铎, 杨子晖, 陈海强

(1. 广东财经大学金融学院, 广州 510320; 2. 南方科技大学商学院, 深圳 518055; 3. 厦门大学王亚南经济研究院, 厦门 361005)

0 引言

资产价格收益的可预测性一直是学术界长期关注并存在广泛争议的话题.对市场参与者、学术研究者和政策制定者而言,准确理解资产价格收益的可预测性无疑具有重大的学术价值和现实意义.从市场参与者的角度来说,优化投资组合需要甄别出资产配置的依据,即识别出未来资产价格收益的可预测变量;从学术研究者的角度来说,研究资产价格收益的可预测性有助于验证有效市场假说,提出新的股票组合业绩基准和发展资产定价理论等;从政策制定者的角度来说,理解资产价格收益的可预测性有助于完善宏观审慎监管工具.

在资产价格收益的可预测性文献中,可预测性检验一般基于如下线性结构模型[1-3]

yt=α+βTxt-1+ut

(1)

xt=Πxt-1+et1≤t≤T

(2)

其中ut和et有可能相关.以上线性结构模型广泛应用于实证经济和金融中,如格兰杰因果关系检验、有效市场假说、资产定价理论以及基金业绩表现等.

由于上述模型中预测变量xt-1(如利率、股利价格比、通货膨胀率等)通常具有高持续性特征[4],其动态演变过程接近单位根过程.同时,ut和et之间的相关系数通常显著为负数[1],因而会出现所谓嵌入式内生性问题(embedded endogeneity).在早期的研究中[2],这种内生性在有限样本下会导致有偏的系数估计和统计检验出现过度拒绝现象,标准的t检验不再适用.为解决这一问题,可能的办法是假定预测变量服从近似单位根过程,其AR(1)系数满足π=1-c/T,其中c为常数,T为样本数.以往文献对这一近似单位根过程系数的渐进性质进行过深入研究[3],然而,由于系数中的常数项c在极限分布中不能被一致估计,很难获得其统计检验的临界值.

近十年来,计量经济学者尝试发展统一的检验方法,而不管预测变量是否具有较强的持续性以及残差是否出现内生性.一种方法是基于Bonferroni方法的Q统计量[1],然而这种方法有可能导致严重的水平扭曲(1)水平扭曲(size distortion)包括过度拒绝和过度接受两种.实证中在显著性水平0.05下,用p值与0.05比较.如果大于0.05,认为不能显著拒绝原假设,如果小于0.05,认为显著拒绝原假设.当仿真中经验水平(empirical size)远大于0.05(过度拒绝)或远小于0.05(过度接受)时,都称之为水平扭曲,那么应该用p值与经验水平比较以作出正确的推断.和检验功效失效问题[5].另一种方法是Phillips 和Magdalinos[6]提出的工具变量法(IVX),其核心思想是构建比预测变量持续性稍小的工具变量.这种方法不仅消除了内生性,而且对预测变量的持续性具有稳健的检验力度.为了检验变量的可预测性,Kostakis等[7]推导出基于IVX的Wald统计量在大样本下服从标准的卡方分布.他们的方法对涵盖平稳过程到单位根过程的预测变量都有稳健的检验力度.Lee[8]进一步把IVX方法扩展到分位数回归中.最近,Yang等[9]提出了对可预测模型的残差同时存在序列相关和条件异方差都稳健的IVX检验.

在中国资产收益率的可预测性实证研究中,近年来学者们从不同的角度展开了很好的分析与阐述.其中,姜富伟等[10]选取不同经济变量研究了中国沪深股票市场收益率的可预测性,包括市场投资组合以及根据公司行业、规模、面值市值比和股权集中度等划分的成分投资组合等.研究结果表明,中国沪深股票市场投资组合和各种成分投资组合都存在显著的样本内可预测性.陈坚和张轶凡[11]利用高频股票数据构造中国沪深股票市场的已实现偏度,发现较低的已实现偏度可以显著预测下个月中国沪深股票市场较高的超额收益率.杨炳铎和汤教泉[12]基于IVX统计检验方法,对我国主要宏观经济变量能否单独或联合预测债券收益率进行可预测性分析,并进一步提出使用AIC和BIC方法对多元变量回归模型进行变量筛选.蒋志强等[13]运用可行拟广义最小二乘法(FQFLS)[14]和8个预测因子对31个投资组合的可预测性进行检验,结果发现中国沪深股市收益率具有可预测性,但各投资组合收益率的可预测性在熊市和牛市等不同市场阶段均存在明显差异.最近,张春玲等[15]对资本市场收益可预测性,特别是股票收益可预测性的研究进展进行了综述,包括预测变量选择和提高收益预测准确性的主要方法等.

纵观该领域的研究,过往的理论文献主要侧重于可预测模型的右侧问题,如预测变量的强持续性和模型残差的内生性以及残差的自相关性[9]等,暂无文献研究可预测模型的左侧问题,如被预测变量存在泡沫与崩盘的情形.而且,在过往文献中常常采用的检验方法,包括IVX检验法[12]、t检验法[11]和Bootstrap法[10],它们在被预测变量存在泡沫与崩盘现象,预测变量存在强持续性和模型存在内生性时,都会有过度拒绝的水平扭曲现象(见表1)(2)FQFLS方法本身就存在过度接受的水平扭曲问题,见参考文献[14]中表1..有鉴于此,本研究对带有泡沫与崩盘的可预测模型进行可预测性检验.在理论建模中,首先在模型中加入哑变量以刻画泡沫与崩盘现象,并对泡沫与崩盘下的可预测模型进行参数估计,并由此构建新的Wald统计量.该统计量不管预测变量属于平稳过程、适度偏离单位根过程、近单位根过程还是单位根过程,在大样本下都会收敛到标准的卡方分布.

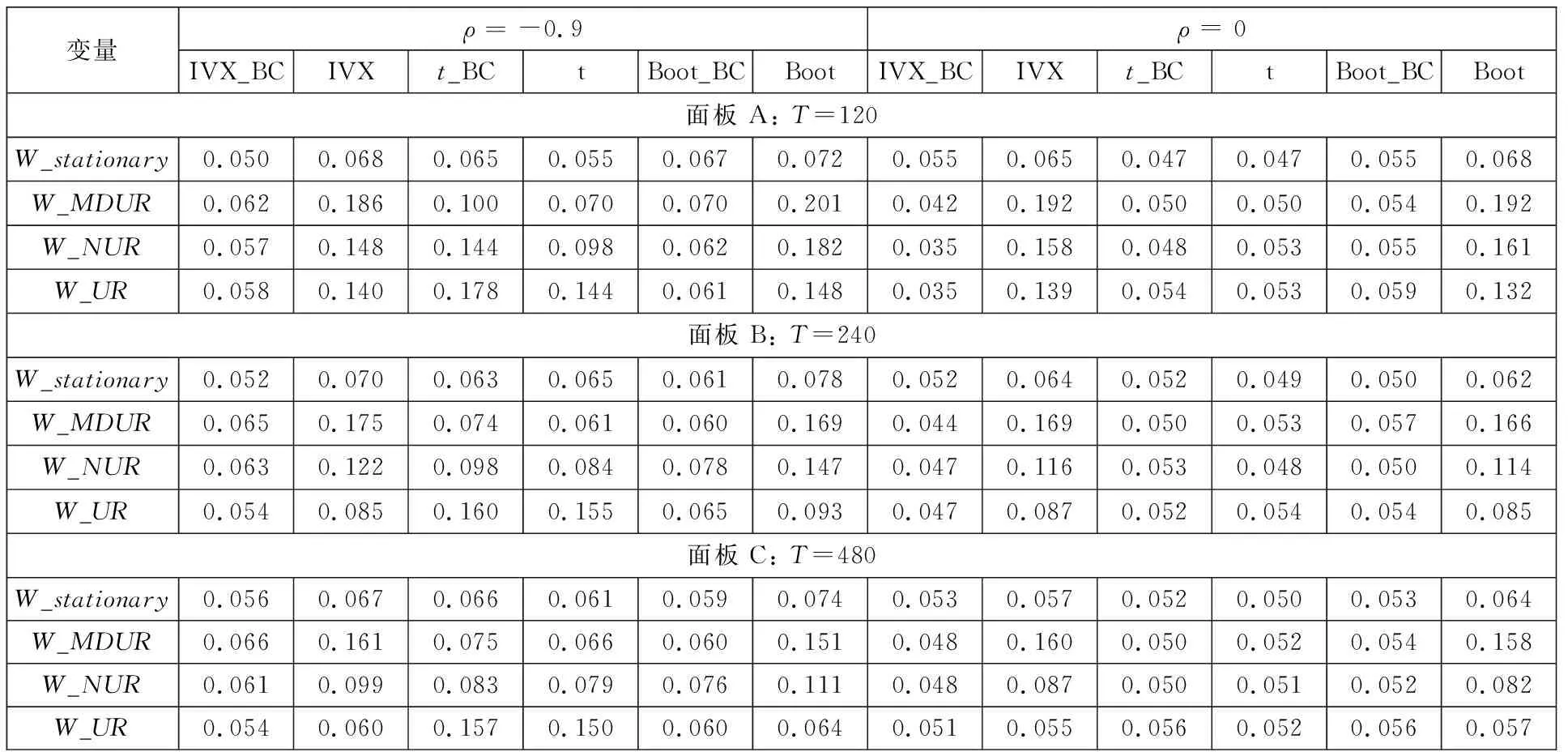
表1 存在泡沫与崩盘的单变量可预测性检验Table 1 Empirical for univariate predictive regression when both bubble and crash exist

在仿真研究中,对存在泡沫与崩盘情形下的IVX检验(IVX_BC)的检验水平(size)和检验功效进行有限样本模拟分析.同时,把检验结果与不考虑泡沫与崩盘情形的IVX检验(IVX)、考虑泡沫与崩盘情形的t检验(t_BC)、不考虑泡沫与崩盘情形的t检验(t)、考虑泡沫与崩盘情形的Bootstrap法(Boot_BC)和不考虑泡沫与崩盘情形的Bootstrap法(Boot)[10,16]这5种方法进行比较研究.仿真结果表明,无论是单变量可预测模型还是多变量可预测模型,以及模型是否存在内生性,本文提出的带有泡沫与崩盘的IVX检验(IVX_BC)均具有很好的检验力度.而IVX检验、t检验以及Bootstrap(Boot)法由于没有考虑泡沫与崩盘的情形,在预测变量高持续性下都存在过度拒绝的水平扭曲现象.t_BC检验和Boot_BC法尽管在一定程度上减少了检验偏差,但在预测变量高持续性情形下仍然存在一定程度的水平扭曲.同时,还考察了泡沫和崩盘时间错误设定的3种情形,本研究提出的IVX_BC检验仍然能得到稳健的结果.最后,还就它们的检验功效进行对比分析.结果表明,与IVX方法相比,本研究提出IVX_BC方法具有更强的检验功效.

在应用分析中,本研究选取涵盖股票市场、宏观经济和债券市场等17个预测变量,对上证指数的月度超额收益率进行可预测性检验.首先使用Phillips等[18]提出的广义Sup ADF(GSADF)方法来检验多个泡沫的存在,并使用递归向后回归技术确定多个泡沫和崩盘的起点和终点.实证中的初步分析验证了可预测变量的高持续性、可预测模型的内生性、预测模型残差的异质性以及上证指数存在泡沫与崩盘现象,正因如此,使用IVX_BC检验对上证指数的可预测性进行研究.在单变量可预测模型中,不管是在全样本还是在部分样本中,考虑了泡沫与崩盘的IVX_BC检验都发现通货膨胀率(CPI)能显著负向预测上证指数.在部分样本中,换手率(TO)也能显著负向预测上证指数.而在多变量可预测模型中,6种变量组合均不具有显著的预测能力.

1 计量模型

考虑以下带有泡沫与崩盘的可预测模型

yt=γ0+γBBt-1+γCCt-1+βTxt-1+ut,

1≤t≤T

(3)

(4)

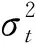
预测变量xt服从向量自回归过程

xt=Πxt-1+et

(5)

Π=Id+C/Tηx

1)平稳过程(cj<0,j=1,…,d,ηx=0);

2)适度偏离单位根过程(cj<0,j=1,…,d,0<ηx<1);

3)近单位根过程(ηx=1);

4)单位根过程(cj=0,j=1,…,d).

显然,以上过程1)～过程4)涵盖了从平稳过程到单位根过程具有不同持续性的预测变量.

估计步骤

为了得到系数β的估计量,把式(3)写成

yt=γTDt-1+βTxt-1+ut

(6)

(7)

(8)

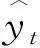
(9)

检验步骤

考虑如下带有q个线性约束条件的假设检验

H0:Hβ=λvs H1:Hβ≠λ

式中H为已知的q×d矩阵;λ为已知的q×1向量.

为了得到基于IVX方法的Wald统计量,令

(10)

(11)

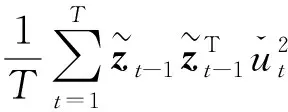
定理1(5)如需定理1的推导过程,可联系作者邮箱获取.假定q是假设检验H0中线性约束条件个数,并假定预测变量xt-1属于过程1)～过程4)中的一种,在满足正则条件下(6)如需正则条件推导过程,可联系作者邮箱获取.,随着样本量T→∞,基于IVX的Wald统计量Wβ会收敛到自由度为q的卡方分布,即

Wβ⟹χ2(q)

定理1表明,不管预测变量xt-1属于平稳过程、适度偏离单位根过程、近单位根过程还是单位根过程,均成立.在大样本下,哑变量系数的估计不影响假设检验H0下Wald 统计量Wβ的渐进分布.

2 有限样本仿真

对IVX_BC检验的检验水平和检验功效进行有限样本仿真研究.同时,把检验结果与IVX检验、t_BC检验、t检验、 Boot_BC法和Boot法[10,16]等5种方法进行比较研究.以下所有结果为显著性水平5%下的双侧检验.

假设数据生成过程如下

yt=γ0+γBBt-1+γCCt-1+βTxt-1+ut,

(12)

t=1,…,T

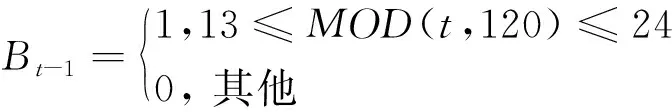
式中Bt-1和Ct-1分别是泡沫与崩盘时期的哑变量,MOD是求余函数,即两个数值表达式作除法运算后的余数.通过以上哑变量设置,每120个月有12个月的泡沫期和12个月的崩盘期,这与我国上证指数近240个月来有两个泡沫和崩盘期,并且每个时期持续时间近12个月一致.同时,根据上证指数月度对数收益率在正常,泡沫和崩盘时期的样本均值(见实证表4),设置γ0=0.001,γB=0.085,γC=-0.101.

为刻画股票收益的厚尾现象和波动的集聚效应,假设残差ut服从以下GARCH(1,1)过程

(13)

式中冲击εt服从自由度为5的学生t分布.

为刻画预测变量的不同持续性特征,假设xt服从AR(1)过程,即

xt=Πxt-1+et

(14)

在单变量可预测模型中,Π=0.2, 0.9, 0.98, 1.0分别对应平稳过程、适度偏离单位根过程、近单位根过程和单位根过程.et=9ρut+0.7vt,vt是个标准正态分布.ρ用来刻画ut和et的相关性,即模型的内生性.在多变量可预测模型中,xt=(x1t,x2t,x3t,x4t)T,Π=diag(0.2,0.9,0.98,1.0)是个对角矩阵.et=(e1t,e2t,e3t,e4t)T,ejt=9ρut+0.7vjt,j=1,2,3,4,vjt是标准正态分布.考虑3种不同样本数T=120,240,480,它们分别对应10年、20年和40年的月份数.由于实证中ρ>0和ρ<0的情况都有出现(见表6),在表1和表2中展示ρ= -0.9, 0, 0.9的检验水平结果.由于运行时间的限制,表中Boot方法本文重复1 000次,其它方法重复10 000次.

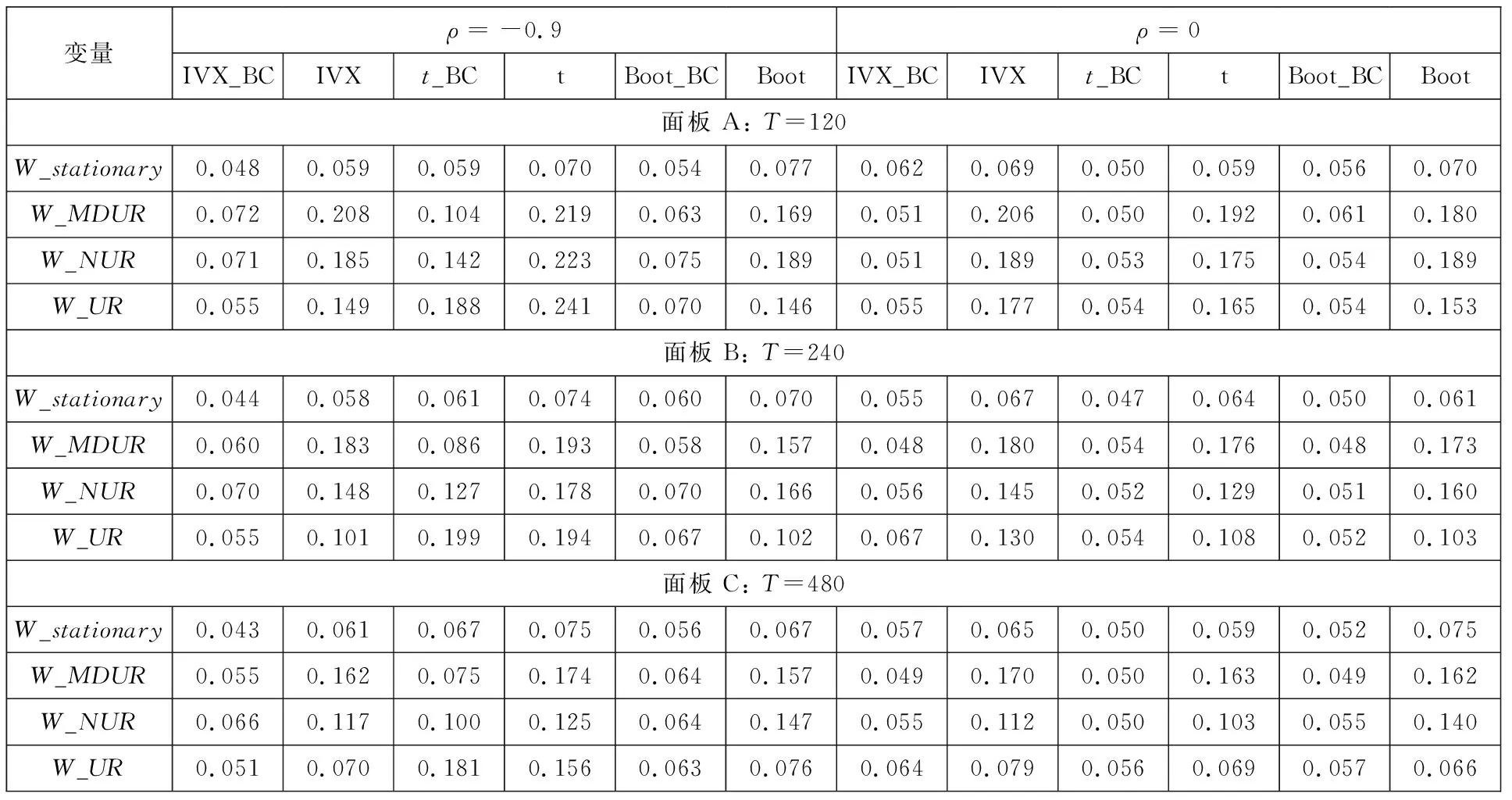
表2 带有泡沫与崩盘的多变量可预测性检验 Table 2 Empirical for multivariate predictive regression when both bubble and crash exist

表1为存在泡沫与崩盘的单变量可预测性检验水平表.在存在内生性(ρ=-0.9, 0.9)条件下,IVX_BC检验能得到正确的检验水平,即接近名义水平0.05;IVX检验在预测变量为适度偏离单位根过程和近单位根过程时都存在过度拒绝的水平扭曲现象,即远远高于名义水平0.05,而且在预测变量为单位根过程和有限样本下同样存在一定程度的水平扭曲现象.同时,还对不考虑泡沫与崩盘情形的普通最小二乘法(OLS)下t检验和t_BC检验的检验水平进行仿真研究.研究发现,不管是t_BC检验还是t检验的结果,当预测变量为适度偏离单位根过程、近单位根过程和单位根过程时,其检验水平都存在过度拒绝的水平扭曲现象.最后,还对文献中Boot法进行仿真(7)有关Boot法的具体步骤,可联系作者邮箱获取..表中结果表明,Boot法同样存在严重的水平扭曲,Boot_BC法能减少水平扭曲,但与IVX_BC相比,在存在内生性时仍然存在一定程度的水平扭曲.

在不存在内生性(ρ=0)条件下,IVX_BC检验同样能得到正确的检验水平.同样地,t、t_BC和Boot_BC都能得到正确的检验水平,而IVX检验和Boot法在预测变量高持续性下都存在过度拒绝的水平扭曲现象.

还对带有泡沫与崩盘的多变量可预测模型进行研究,其检验水平表见表2.发现表2的结果与表1类似,不管是否存在内生性,IVX_BC检验都得到正确的检验水平.IVX、t、t_BC和Boot法在内生性条件下都存在过度拒绝的水平扭曲现象.考虑了泡沫与崩盘情形时,Boot_BC法都能减少水平扭曲.当不存在内生性(ρ=0)时, IVX_BC检验、t_BC检验和Boot_BC检验都能得到正确的检验水平;但在存在内生性(ρ= -0.9, 0, 0.9)和预测变量高持续性下,t_BC检验和Boot_BC检验仍然存在一定程度的水平扭曲.最后,与单变量可预测模型结果(见表1)相比,多变量可预测模型结果(见表2)波动更大.

为了验证本模型检验的稳健性,对泡沫和崩盘时间错误设定的3种情形进行仿真研究,包括泡沫和崩盘时间设定比真实时间增加20%(IVXBC1),泡沫和崩盘时间设定比真实时间减少20%(IVXBC2)和真实数据的产生是无泡沫和崩盘过程(IVXBC3).表 3为这3种情形下IVX_BC检验的稳健性检验水平表.从表中可以看到不管是否存在内生性,即不管ρ是否为0,这3种情形的检验水平都不存在水平扭曲,即值都接近0.05.以上3种情形的仿真结果表明,本研究提出的可预测模型检验结果对泡沫和崩盘时间错误设定稳健.

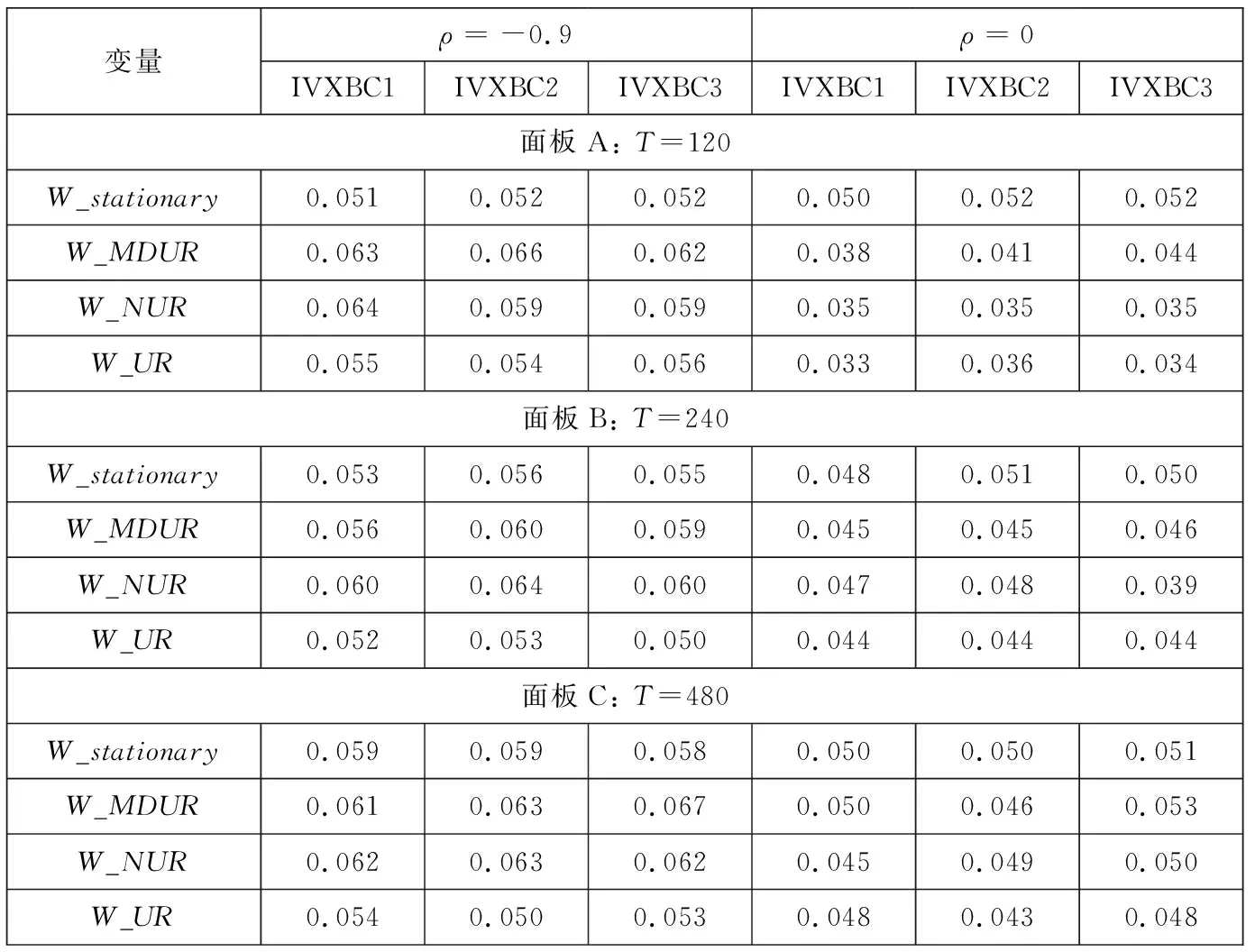
表3 泡沫与崩盘时间错误设定下IVX_BC稳健性检验Table 3 Empirical size for IVX_BC test when the periods of both bubble and crash are misspecified

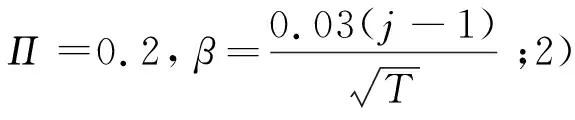
图 1为这4种方法分别在Π=0.2,0.9,0.98,1.0的检验功效比较图.从图中可以看到,与平稳过程Π=0.2)相比,近单位根过程(Π=0.98)和单位过程(Π=1.0)检验有更强的功效,这是由于强持续性预测变量估计系数的收敛速度比平稳变量更快.当预测变量为平稳过程(Π=0.2)时,IVX_BC检验功效比IVX强.与t_BC检验的检验功效相比,IVX_BC检验功效会略有损失,但损失不大.这是由于在预测变量平稳条件下,OLS估计量是最有效的.当预测变量为适度偏离单位根过程(Π=0.9)时,IVX检验在β=0时会有水平扭曲,偏离0时,检验功效会比IVX_BC弱.当预测变量为强持续性过程(Π=0.98,1.0),IVX检验,t检验和Boot法在β= 0时都有水平扭曲,并且偏离0时,IVX检验功效会比IVX_BC弱.

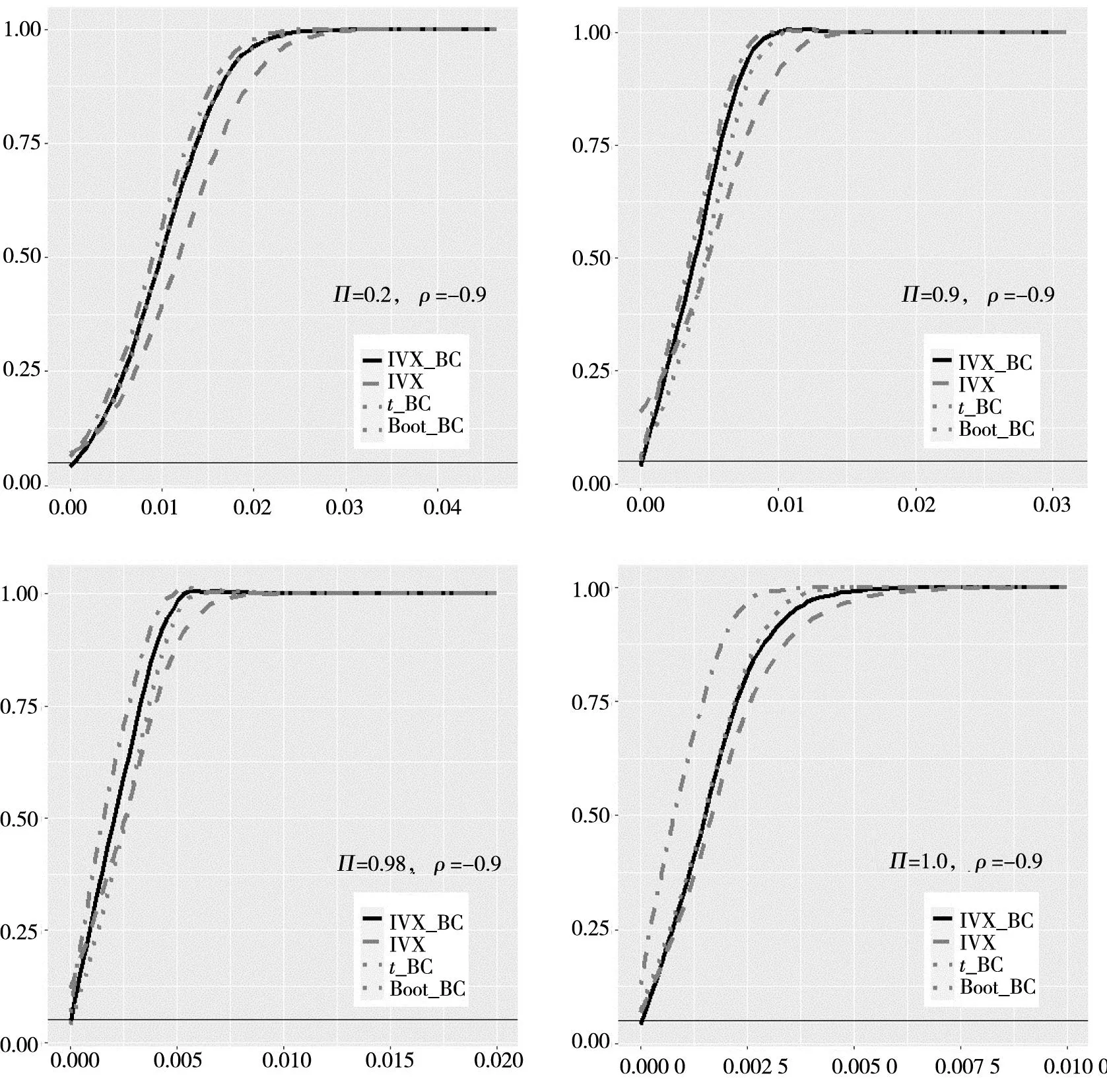
图1 预测变量下4种方法的检验功效比较Fig.1 Power plots for four testing methods with single regressor

从以上仿真可以看到,由于考虑了泡沫与崩盘的情形,不管是在单变量可预测模型还是在多变量可预测模型,也不管是否存在内生性,本研究提出的IVX_BC检验都能给出正确的检验水平.而IVX检验、t检验和Boot法由于没有考虑泡沫与崩盘的情形,在预测变量高持续性下都存在过度拒绝的水平扭曲现象.t_BC检验和Boot_BC检验尽管在一定程度上减少了检验偏差,但在预测变量高持续性下仍然存在一定程度的水平扭曲.同时,IVX_BC检验对泡沫与崩盘时间错误设定的3情形稳健,包括泡沫与崩盘时间设定比真实时间增加20%,泡沫与崩盘时间设定比真实时间减少20%,和真实数据产生过程无泡沫与崩盘过程.最后,本研究提出的IVX_BC检验功效比IVX 检验强,与t_BC检验相比,检验功效损失不大.

3 实证检验

本研究选取的被预测变量为上证指数的月度对数超额收益率,其计算公式为yt=ln(1+Rt)-ln(1+rf),其中ln(·)为自然对数变换,Rt是上海证券交易所发布的上证指数简单收益率,rf是市场无风险利率,他们均来源于国泰安(CSMAR)数据库.数据区间为1999年1月—2019年1月,选择多1个月数据是因为做可预测回归时,滞后1期自变量的存在导致实际使用的数据会少1个月.由于绝大部分文献[7]都使用月度数据,仅有少部分文献在研究长期预测时用到季度或者年度数据.因此,本研究使用月度样本数据对上证指数进行可预测性检验.

在预测变量的选择上,参考国内外可预测检验相关文献[35],选择涵盖股票市场,宏观经济和债券市场等17个变量.

股票市场预测变量包括股利支付率(D/E)、股利价格比(D/P)、股息率(D/Y)、盈余价格比(E/P)、账面市值比(B/M)、股票方差(svar)、净权益增加(ntis)和换手率(TO)等.具体来说,D/E等于总股利的自然对数减去总盈余的自然对数,其中总股利是过去12个月(包括当月)的上证所有A股股利移动加总.本研究设定当年4月至下一年3月的总盈余来自上一年度年报.D/P等于总股利的自然对数减去总市值的自然对数.D/Y等于总股利的自然对数减去滞后1期市值的自然对数.E/P等于总盈余的自然对数减去总市值的自然对数.B/M等于总账面价值除以总市值,其中总账面价值是上海证券交易所所有A股上市公司资产合计的总和.由于每年4月底前公布上一年度年报,10月底前公布当年中报,设定当年4月至9月的资产合计来自上一年度年报,当年10月至下一年3月的资产合计来自当年中报.svar是当月上证指数日收益率的平方和.ntis等于过去12个月上证A股新股发行总量移动加总除以当月总市值,其中新股发行总量=当月总市值-前一个月总市值×(1+当月上证指数收益率).TO等于月度总交易量除以月度总市值.在数据来源上,总盈余来自Wind数据库上市公司年报,资产合计来自Wind数据库上市公司年报和中报,其它数据均来自国泰安数据库.由于有部分预测变量在计算时需要用到过去1个月,甚至过去12个月的数据,因此收集的原始数据都从1998年1月开始.

宏观经济指标包括消费者价格指数(CPI)和生产者价格指数(PPI).由于CPI和PPI一般在下一个月公布,本研究使用前一个月同比值作为当月数据,数据均来自Wind数据库.

债券市场预测变量包括长期到期收益率(lty)、期限利差(tms)、违约收益利差(dfy)、短期国债利差(sts)、长期国债利差(lts)和国债收益率(tbl)等.具体来说,lty为10年中债地方政府债到期收益率(AAA).tms等于10年中债地方政府债到期收益率(AAA)减去3个月中债国债到期收益率.dfy等于10年中证公司债到期收益率(A)减去10年中证公司债到期收益率(AAA).sts等于3个月中债国债到期收益率减去1个月中债国债到期收益率.lts等于10年中债国债到期收益率减去1年中债国债到期收益率.tbl是3个月中债国债到期收益率.由于数据的限制,lty和tms从2010年10月开始,dfy从2014年12月开始,lts和tbl从2002年1月开始.以上原始数据均为Wind数据库日度数据,本研究对它们进行了月内平均处理.

假定上证指数月度对数收益率全样本由泡沫时期、崩盘时期和正常时期3个样本组成.借鉴Phillips等[17]提出的广义sup ADF(GSADF)方法来确定泡沫时期和崩盘时期的起点和终点.GSADF统计量定义如下

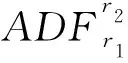
1)对上证指数日度数据进行GSADF正向检验,得到多个泡沫时期的起点和终点;

2)对上证指数日度数据进行GSADF反向检验,得到多个崩盘时期的起点和终点;

3)假定泡沫时期和崩盘时期为2个月以上(包括2个月),并且每个月至少有5个交易日属于以上两个步骤的泡沫或者崩盘时期;

4)如果泡沫时期和崩盘时期月份有重合,指数顶点左侧设置为泡沫时期,右侧设置为崩盘时期.

以上基于GSADF检验得到泡沫和崩盘时期的起点和终点可以借助R统计软件中的psymonitor程序包来完成.根据以上4个步骤,识别出泡沫时期包括2006年5月—2006年7月、2006年9月—2007年10月和2014年11月—2015年5月共计24个样本(见图2深灰色区间).崩盘时期包括2004年3月—2004年4月、2007年11月—2008年3月、2008年5月—2008年6月、2008年8月—2008年11月、和2015年6月—2015年7月共计15个样本(见图2浅灰色区间).正常时期是全样本中除去泡沫时期和崩盘时期这两个时间段,共计201个样本.全样本及其3个子时期样本的描述性统计见表4.从表中可以看到,全样本和正常时期样本的均值都为接近0的正数,但最大跌幅和最大涨幅按对数收益率计算分别高达-28.2%和27.8%,说明上证指数在极端月份波动很大.特别是,在泡沫时期月度平均对数收益率高达8.5%,而在崩盘时期月度平均对数收益低至-10.1%.在波动率上,崩盘时期的波动率比正常时期高78%,甚至比泡沫时间高50%.

注:黑色线为上证指数走势,深灰色和浅灰色区间分别为泡沫时期和崩盘时期.图2 基于GSADF识别的泡沫和崩盘时期Fig.2 Bubble and crash periods identified by GSADF procedure

表4 上证指数的月度对数收益率描述性统计Table 4 Summary statistics for monthly log return of Shanghai securities composite index

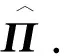
表5 预测变量单位根检验Table 5 Unit root tests for predictive regressors

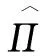
为验证可预测模型中泡沫与崩盘的存在,用上证指数对带有泡沫与崩盘的单预测变量进行OLS回归.表 6为全样本(1999年1月—2019年1月)和部分样本(2009年1月—2019年1月)下对泡沫和崩盘哑变量的t检验结果.全样本240个月包含2007年—2008年和2014年—2015年2个泡沫与崩盘过程,部分样本120个月只包含2014年—2015年1个泡沫与崩盘过程.由于数据的限制,变量sts、lts和tbl在全样本中的数据从2002年1月—2019年1月,变量lty和tms在部分样本中的数据从2010年8月—2019年1月,变量dfy在部分样本中的数据从2014年12月—2019年1月.

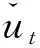
由于可预测变量的高持续性(见表5)、预测模型的内生性(见表6)、预测模型残差的异质性(见表6)以及上证指数存在泡沫与崩盘现象(见表6),这使得必须使用IVX_BC对上证指数的可预测性进行研究.为了方便比较,还同时展示IVX检验、t检验、Boot法以及把泡沫与崩盘作为哑变量放入模型的t_BC检验和Boot_BC法.Boot得到的统计量和t值相同,但由于构建的置信区间不一样,会导致Boot法得到的显著性和t检验不一致.

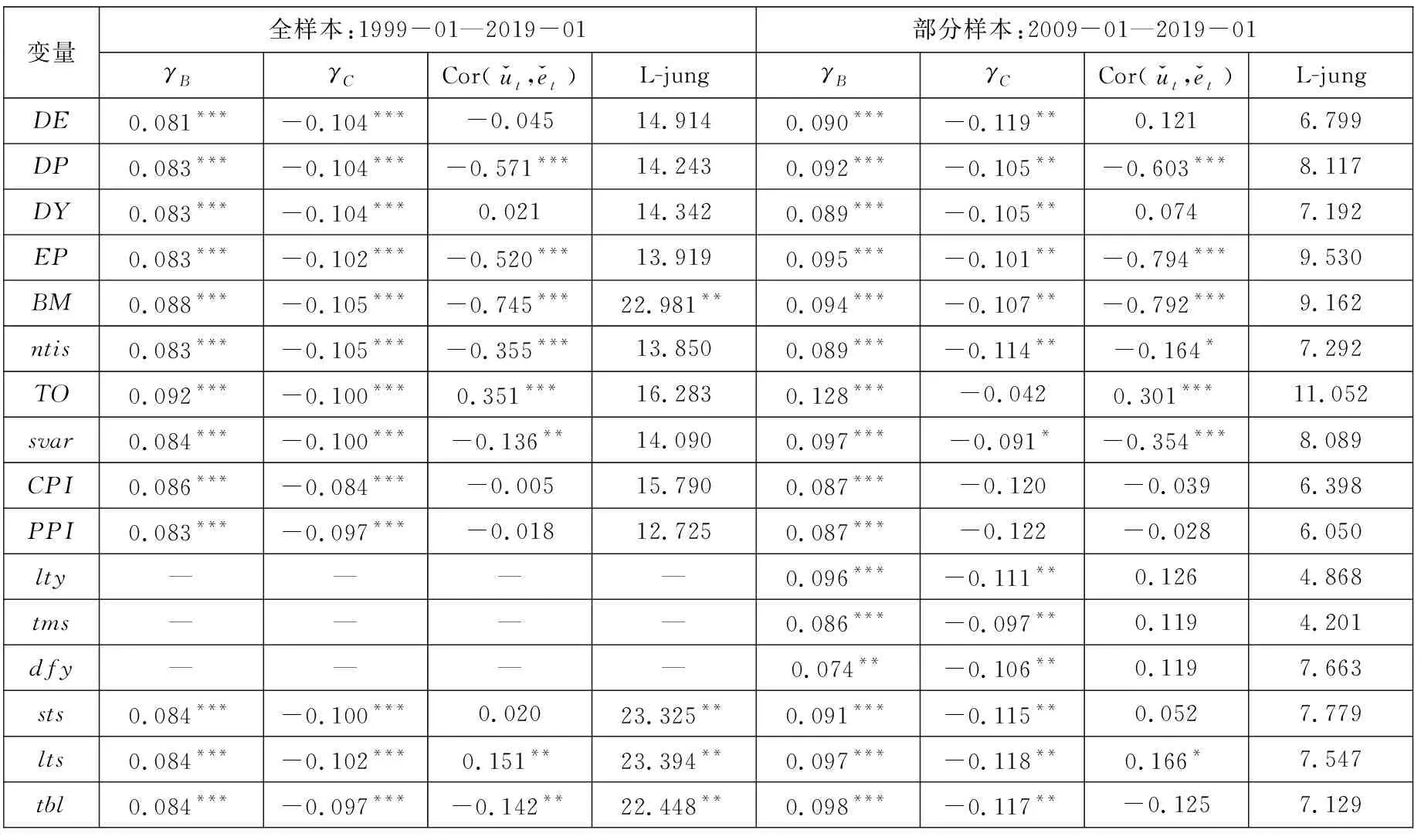
表6 带有泡沫与崩盘的单预测变量OLS回归结果Table 6 OLS regression results forunivariate predictive regression when both bubble and crash exist

表 7为以上6种方法在单变量可预测回归模型中的检验结果.从表中可以看到,在全样本中,IVX检验,t检验和Boot法都认为nits、PPI、sts和tbl在1%或5%水平下显著,而IVX_BC,t_BC检验和Boot_BC法都认为不显著.对于预测变量EP,IVX检验和t检验都认为ntis在5%水平下能显著预测上证指数,而其它方法不管在哪个显著水平下都认为EP不能用来预测上证指数.对于预测变量CPI,IVX检验,t检验和Boot法都认为CPI在1%水平下能显著预测上证指数,而t_BC和Boot_BC法认为CPI在5%水平下能显著预测上证指数,IVX_BC检验仅认为CPI在10%水平下显著.6种方法都认为DE、DP、DY、BM、TO、svar和lts这7个预测变量都不能用来预测上证指数.

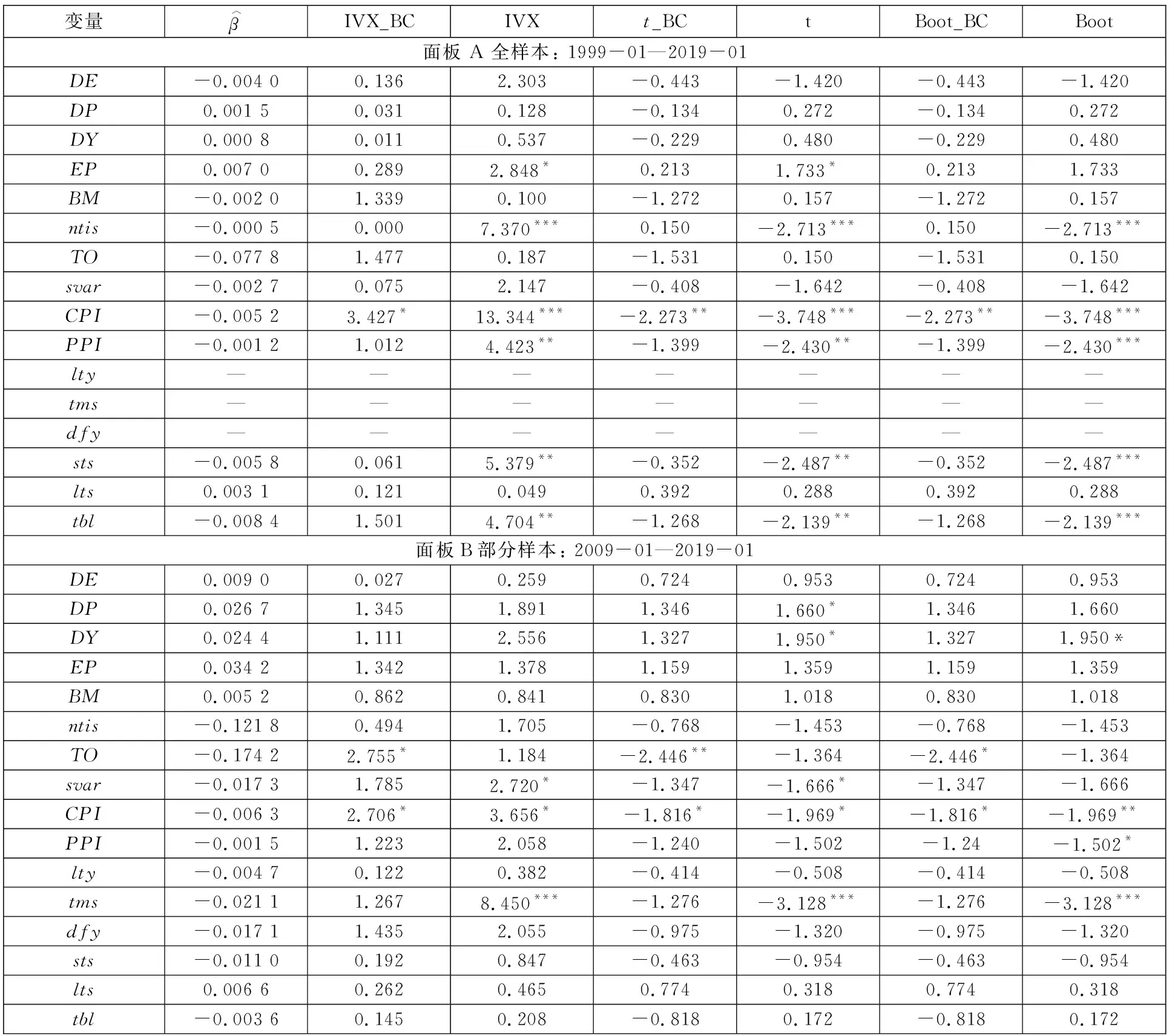
表7 单变量可预测回归模型检测结果Table 7 Testing results for univariate predictive regression

在部分样本中,t检验认为DP在10%水平下能显著预测上证指数,t检验和Boot法认为DY在10%水平下能显著预测上证指数,而其它检验都认为DP和DY不显著.IVX_BC、t_BC和Boot_BC法认为TO分别在5%或10%水平下能显著预测上证指数,而不考虑泡沫与崩盘的其它3种检验都认为其不显著.IVX检验和t检验认为svar在10%水平下能显著预测上证指数,而其它4种检验均认为其不显著.6种检验均认为CPI在5%或10%水平下能显著预测上证指数.对于预测变量tms,IVX检验,t检验和Boo法都认为其在1%水平下能显著预测上证指数,而IVX_BC,t_BC和Boot_BC法认为其不能显著预测上证指数.6种方法都认为DE、EP、BM、ntis、lty、dfy、sts、lts和tbl这9个预测变量都不能用来预测上证指数.

也考虑把交叉相乘项Bt-1xt-1和Ct-1xt-1放入到单变量可预测模型中,结果显示,基于IVX_BC检验的交叉项系数都不显著.这表明可预测变量在泡沫时期或崩盘时期的可预测能力与全样本时期的结论无明显差异.由于篇幅的限制,不展示加入交叉相乘项的可预测模型检验结果.

综上,不管是在全样本还是在部分样本中,IVX_BC检验都认为CPI在10%水平下能显著负向预测上证指数.在部分样本中,TO也在10%水平下能显著负向预测上证指数.姜富伟等[10]认为,DY、CPI和TO都能用来显著预测市场投资组合收益,而IVX_BC检验仅认为CPI和部分样本中的TO能显著预测上证指数,DY不能用来预测上证指数.与IVX_BC检验相比,IVX法、t_BC法、t法和Boot法会出现过度拒绝现象,而Boot_BC仍然存在一定的过度拒绝现象.以上实证结果与上一节中的仿真结果一致.

在多变量可预测回归模型检验中,考虑了以下6种变量组合(a)DY和tbl[16];(b)DP和tbl[20];(c)EP、BM和tms[27];(d)DE和DP[28];(e)DP和BM[29];(f)DP、tms、dfy和tbl[30].受样本数据的限制,周开国等[16]与Ang和Bekaert[20]的数据从2002年1月—2019年1月,Ferson和Schadt[30]的数据从2014年12月—2019年1月,而Campbell和 Vuolteenaho[27]的数据从2010年8月—2019年1月.

表8为以上6种组合在带有泡沫与崩盘的多变量可预测回归模型检验结果.从表中可以看到,6种组合在10%水平下都认为预测变量组合均联合不显著.就组合中的单个变量而言,Kothari和Shanken[29]组合中的BM在10%水平下能显著负向预测上证指数,而Ferson和Schadt[30]组合中的tms和tbl在5%水平下能显著负向预测上证指数.在DY和tbl组合中,不管是单个变量还是组合变量,它们都不能用来预测上证指数,这与周开国等[16]的结论一致.

4 结束语

资产价格收益的可预测性一直是学术界长期关注并存在广泛争议的话题,准确理解资产价格收益的可预测性无疑对市场参与者、学术研究者和政策制定者都具有重大的学术价值与现实意义.本研究对带有泡沫与崩盘的可预测模型进行可预测性检验.在理论构建中,推导出带有泡沫与崩盘的Wald检验方法,该统计量在大样本下将遵循标准的卡方分布.这一性质不仅对预测变量的不同持续性(包括平稳过程、适度偏离单位根过程、近单位根过程和单位根过程)以及可预测模型的内生性稳健,而且在被预测变量普遍存在泡沫与崩盘现象下依然稳健.

在有限样本仿真中,本研究提出的带有泡沫与崩盘情形的IVX检验(IVX_BC)能给出正确的检验水平(size)和强大的检验功效(power).而其它5种方法,包括不考虑泡沫与崩盘情形的IVX检验(IVX)、考虑泡沫与崩盘情形的t检验(t_BC)、不考虑泡沫与崩盘情形的t检验(t)、考虑泡沫与崩盘情形的bootstrap法(Boot_BC)和不考虑泡沫与崩盘情形的bootstrap法(Boot)都存在“过度拒绝”的水平扭曲现象.