面向相位动态优化的交叉口智能控制方法

魏丽英， 丁粲容， 艾子妍， 管姝雯

（北京交通大学 交通运输学院, 北京 100044）

当下我国的信号交叉口大多使用固定相位和配时方案，不能很好地适应复杂的交通流变化.相位控制中，增加相位个数可以有效减少车流冲突，降低交通事故发生，但是同时也会使信号周期时间变长，进而导致车辆通行效率降低、固定延误增加.同时，在平峰时段过长的绿灯时间以及不合理的绿信比会导致绿灯空放，而在高峰时段面对拥挤的车流，过短的绿灯时长也会导致停车次数增多，造成交通延误.由于交通量随着时间动态变化，不同时间段适合的相位、配时方案也不同，而动态信号控制方案可以适应动态交通流变化，有效减少延误并提高通行效率.

相位设计方面，现有研究大多是以固定相位、相序为主，对相位进行智能选择和动态优化的研究较少.张雷元等［1］提出相位设计4 阶段法，分为交通流分析、专用相位设计、相序设计和相位方案检验.张国华［2］根据交通流冲突点数量、交叉口时空利用率、信号相位损失时间总和3 项指标评估相位方案.黎昉［3］使用图论法确定最佳相位数，并采用动态聚类分析法确定最佳相序.Ambili 等［4］根据交通冲突关系将交通流建模为不相容图，将相位设计问题转化为顶点着色问题，寻求最佳相位设计方案.Zhai 等［5］采用枚举法确定下一信号阶段的最佳相位设计及其允许的最大相位时间.以上学者多聚焦于固定的相位方案评估决策或利用图论等方法将相位设计转化为数学问题.在实际交叉口，车流实时变化，左转车流是交通流冲突的重要因素，应在相位设计过程中着重考虑左转车流的影响.配时优化方面，许多学者采用蚁群算法、遗传算法等启发式算法求解信号配时优化模型.慕飞飞等［6］建立以减少平均停车次数和平均延误为优化目标的非线性信号配时数学模型，使用遗传算法求解.黄敏等［7］改进蚁群算法，以求解传统的单点交叉口信号配时优化问题.徐明杰等［8］采用动态加权系数将多目标问题转化为单目标，并提出改善稳定性的粒子群算法求解模型.Yuan 等［9］基于交叉口交通流特征随时间变化的实际情况，以延误、停车次数和排队长度为多目标建立优化模型.Zhao 等［10］提出结合遗传算法与机器学习的智能交通信号求解算法，以减少交叉口车辆总延误. 现有研究的热点和侧重点大多集中在优化模型的目标选择和提高求解效率的智能算法等方面.对建立的多目标优化模型进行求解是当前的研究热点之一，其中，如何确定各优化目标的权重是其难点.也有学者同时对相位和配时方案进行综合优化，部分学者采用相位矩阵，将相位量化表示，并代入配时模型中实现相位和配时综合优化.李硕等［11］利用相位矩阵量化相位相序，代入信号配时优化模型中，采用智能信号控制算法同时对信号配时和相位相序进行优化.黎强［12］以交叉口总交通延误最小作为优化目标，以信号相位矩阵和有效绿灯时间作为优化变量，使用遗传算法求解.刘邓［13］提出使用精英多种群遗传粒子群算法求解交叉口相位设计和信号配时组合优化问题.目前的研究大多在信号配时优化模型中对相位方案进行量化表示，没有强调相位方案与车流特征的匹配.在信号控制方案设计时，可以先考虑车流实时特征，选择合适的相位设计方法，再根据多方面效益进行配时优化.

综上，针对十字交叉口多采用固定相位方案的现状，本文提出一种依据左转车通行能力优化相位的新思路.首先，建立1 个相位库，由常用的二相位、三相位和四相位形式组成.然后，以各流向的实时交通量等参数为依据，设计基于左转车通行能力的相位选择原则，寻求适应交通流的实时相位方案，实现动态相位选择，并据此建立模型进行多目标信号配时的优化，模型中选用两种权重体系，第1 种基于Pareto 最优解集采用变异系数法求解得到，第2 种采用指标系数法得到.通过综合优化信号相位和配时方案提高交叉口整体通行效率.

1 动态可变相位控制方案设计

在相位设计中，考虑到驾驶员的认知和驾驶习惯，以经典的相位通行权组合方式为基准建库，避免特别大的相位跳跃导致驾驶员反应不及时触发危险，以3 种基本相位建立相位库，分析各相位特点：二相位控制下，十字交叉口不设置左转保护相位；三相位在1 组对向进口方向设置左转保护相位；四相位在2 组对向进口方向均设置左转保护相位.根据3 种基本相位概念和特征，将各相位方案根据左转保护相位的设置方式进行区分，因此，通过对比左转车通行能力与实际左转交通流量实时判断是否设置左转保护相位，进一步根据左转保护相位的设置方式选择相位方案.

左转保护相位的设置还需要考虑安全因素，其设置与否通常需要综合考虑道路通行能力、交通安全以及车辆延误等.如相位数增多可提高交通安全性，同时也会在一定程度上降低车辆通行效率，因此，高峰时段可以设置左转保护相位以减少交通冲突，平峰时段不设置左转保护相位以提高交叉口效率.研究假设交叉口的设计在仅使用二相位时，其需要考虑的风险在可接受程度内， 相位通行权组合方案都能满足安全要求.

1.1 左转保护相位设置原则

文献［14］提出的左转保护相位设置原则主要以左转车流量为判断依据，对直行车交通量以及车流实时变化情况考虑较少，应用范围存在一定局限.考虑到不同流量下直行车流与左转车流的相互影响程度不同，本文提出一种适应动态交通流的左转保护相位设计原则：以可穿越间隙理论计算得出在非左转保护相位下左转车流的最大穿越流量，以此为左转车通行能力，通过对比当前左转车流量与左转车通行能力决定是否需要设置左转保护相位，进而选择相位控制方案.

1.2 左转车通行能力计算方法

目前在分析无左转保护相位交叉口的车流运行特征时，文献［15］将车流运行状态分为利用绿灯初期抢先通过、利用直行车流的可穿越间隙通过、利用黄灯时间通过3 个阶段.

考虑实际中，左转车道与对向直行车道可能在红灯时长内已经形成车队，车队通过交叉口时可看作直行方向的车队优先通过交叉口后，左转车队再通过交叉口，此时由于左转车队之间跟车距离较近，直行车难以从中穿过，刚到达的对向直行车不具有绝对优先权.待两流向的车队清空时，左转车在直行车到达的间隙中通过.在参考文献［15］的基础上，将1 个绿灯时段内左转车通过无左转保护相位交叉口的过程细分为4 个阶段.

阶段1：利用绿灯初期通过.发生于冲突点距离左转车停车线近的交叉口，绿灯初期，左转车率先驶过冲突点，此时与直行车流暂无冲突.利用绿灯初期通过的车辆数n1为

式中：t直，t左分别为直行车、左转车从停车线到达冲突点的时间；tf为左转车的随车时距.

阶段2：排队通过.当第一辆直行车驶至冲突点时，基于直行优先的原则，在红灯时间内到达并停车等待的直行车辆形成车队先通过，之后其对向左转车队即可排队通过.直行车排队消散的时间t1为

式中：tg为绿灯时间；C为信号周期时长；q直为直行车流平均到达率；tf直为连续两辆直行车通过停车线的平均时间间隔，可取2.0 s；N为某方向的车道数.

排队通过的左转车辆数n2为

左转车流的消散时间t2为

式中：q左为左转车流平均到达率；tf左为连续两辆左转车通过停车线的平均时间间隔，可取3.094 s.

阶段3：利用对向直行车流的间隙通过.此阶段的时间为绿灯时间内，直行和左转车队消散后的时间t3为

某段时间内通过十字交叉口的车流量作为离散变量服从Poisson 分布，假设直行车辆车头时距ht服从交通流率为vp的负指数分布［16］，分布函数为

式中：n为左转车辆数；ht为对向直行车流的车头时距；φ，vp均为对向直行车流到达率；tc为左转车临界间隙.

当ht>tc+ntf时，允许通过(n+1)辆左转车.文献［17］通过实验对左转车临界间隙标定为3.4 s，同时也给出了在对向直行车具有绝对优先权条件下左转车的临界间隙推荐值为5 s，基于左转车临界间隙受到不同驾驶员驾驶习惯的影响难以进行标定，为使建模不过于理想化并考虑安全性，取左转车临界间隙为5 s，随车时距为3.094 s.

故两辆直行车之间出现的间隙能通过n辆左转车的概率Pn为

在一队直行车流间隙中，左转车流通过交叉口车辆数的加权平均值E为

式（9）即为1 个直行车流间隙.若1 h 内有vp个间隙，则1 h 左转车的通行能力cn为

每个进口在t3时段内可穿插通过的左转车的最大车辆数n3为

如果绿灯时间不足以使左转车成队通过，甚至是直行车也无法全部通过，则可以直接设置左转保护相位.即第3 阶段发生时需满足

阶段4：利用绿灯间隔时间通过.假设当交叉口黄灯亮起时，除已超越停车线的车辆外，其他车辆不可继续通行.将每周期可以利用绿灯时间间隔通过的车数计为n4，其数值取决于交叉口的大小，是固定值，一般取0~3 辆.

综上所述，在1 个周期内，可通过的左转车辆数nL为

左转车道的通行能力c左为

根据式（14）即可计算出各进口道的左转车通行能力.以上推理得到的左转车通行能力是非左转保护相位下的，表示左转车在对向直行车影响下的最大通过能力.

1.3 相位方案选择原则

为了使模型更接近现实，做出假设：机动车到达时间间距服从负指数分布；左转车在直行车通行间隙中通过交叉口时，遵循直行优先原则；行人流量不超过人行横道饱和流量，且能够在1 个周期内通过交叉口；交叉口设计情况能使其满足传统的二相位、三相位、四相位控制.

根据文献［18］，选取饱和度作为信号控制交叉口服务水平的评价指标.服务水平的确定方法见表1，饱和度大于0.8时对应比较拥堵和严重拥堵状态.

表1 信号交叉口服务水平Tab.1 Level of service for signalized intersections

对左转相位判断参数取值适用性进行探讨，绘制了一定条件下（以周期时长为120 s，绿信比为0.45，左转车通行能力为1 200 pcu/h 为例），HCM2010 模型中机动车延误随饱和度的变化曲线，见图1.由图1 可知，饱和度达到0.8 以后，车辆延误快速增加.同时，相位数增加往往会带来周期时长以及相位损失时间的增加，导致机动车延误与行人延误突变增长.因此建议：若各进口实际左转车到达流量均小于其左转车通行能力的80%，则选择二相位；若南北方向或东西方向其中1 组，有至少1 个进口道的实际左转车到达流量大于其左转车通行能力的80%，则选择三相位；若南北方向或东西方向这两组中，均有至少1 个进口道的实际左转车到达流量大于其左转车通行能力的80%，则选择四相位.

图1 HCM2010 模型的车辆延误随饱和度的变化情况Fig.1 Variation of vehicle delay with the degree of saturation in the HCM 2010 model

2 多目标配时模型

2.1 多目标函数的确定

交通信号控制方案中各个效益评价指标参数相互关联，多个不同的交通信号优化目标之间也不是相互独立的，比如周期时长的增加会增大道路通行能力，同时会造成信号损失时间和绿灯间隔时间增加，进而导致机动车延误增加；在周期时长增加时，由于等待时间过长，行人延误也会增加.所以在信号控制方案中需要同时优化多个目标，使整体交通效益综合优化.本研究建模时选择机动车车均延误、行人延误和停车率3 个指标进行优化.先计算每辆车的车均延误，再将总延误与车辆数之比作为所有机动车车均延误，其他指标同理.

2.1.1 机动车车均延误

HCM2010 机动车车均延误模型中每辆车平均延误d为

式中：d1、d2、d3分别为均匀延误、随机附加延误、初始排队附加延误，s/pcu.

在计算周期起始时，无初始车辆在交叉口排队，则d3=0 s/pcu［19］.均匀延误d1与随机附加延误d2分别为

式中：CAP 为车道组的通行能力；λ为绿信比；C为周期时长；T为分析时段持续时间，一般取0.25 h；e为信号控制类型校正系数；x为车道组饱和度.

2.1.2 行人延误

在无干扰信号的控制条件下，1 个周期内行人过街平均延误P为［20］

式中：p为行人到达流率；r为人行横道行人饱和流量.

2.1.3 停车率

停车率指在交叉口处停车的车辆占通过交叉口车辆总数的比率［21］.1 个周期内的车辆停车率h为

式中：μ为停车率修正系数，一般取值0.9；ge为有效绿灯时间；y为流量比；S为车道组的饱和流量；q为车流到达率.

2.2 多目标信号配时约束条件

2.2.1 绿灯时间约束

绿灯时长应满足行人安全过街的条件，应当设置最小绿灯时间. 行人过街所需的最小绿灯时间gmin为

式中：Lp为人行横道长度；Vp为行人步行速度，一般取1.0~1.2 m/s；I为绿灯间隔时间.

若某相位的绿灯时间过长时，其他相位红灯等待时间也会过长，从而导致该进口排队长度超出进口道限制.因此，绿灯时间应设置最大范围值，参考文献［14］中的经验值60 s.

2.2.2 信号周期时长约束

交叉口信号周期过短，会使部分相位的绿灯时长无法满足行人通行和车辆安全驶离交叉口所需的最小绿灯时间，也会增加单位时间内相位切换频率，进而增加绿灯时长损失，导致交叉口通行能力的下降.设置最小周期时长Cmin为

式中：Y为各相位最大流量比yimax之和；设一个周期内有pnum个相位，i表示相位数，L为相位总损失时间，其值为各相位的损失时间li之和.

随着周期时长不断增加，通行能力的增速越来越缓，但车辆延误却快速增大.且各相位的红灯时长也随之增加，各进口车道组的排队长度持续增长，很可能导致排队溢出，最大周期时长Cmax为

式中：Rimax为各相位允许的最长红灯时长.

最大周期时长可采用经验值，一般取180 s.

2.2.3 饱和度约束

若交叉口各相位饱和度过小，车流运行顺畅，则交通信号控制意义不大；若交叉口饱和度过大，与实际不符，需设置最小和最大饱和度.参考文献［18］，设置最小饱和度为0.6，最大饱和度为1.0.饱和度x的计算式为

2.3 多目标信号配时模型

设定优化指标为机动车车均延误、停车率和行人人均延误，设置绿灯时间约束、信号周期时长约束以及饱和度约束，建立模型求解最优绿灯时间.

模型中假设1 个周期有pnum个相位，有效绿灯时间集合为G={ge1，ge2，…，gepnum}.多目标信号配时优化模型为

3 模型求解算法

3.1 遗传算法

使用传统的数学方法难以求得多目标配时优化模型的全局最优解.遗传算法［22］是一种自适应全局随机搜索算法，对目标函数的数学特性几乎没有任何要求，适合很多传统数学求解方法无法解决的问题.通过6 个步骤实现遗传算法.

步骤1：设置参数.将初始种群规模、变异概率、交叉概率、最大迭代次数、染色体条数以及各种约束条件设置合适的数值.较大的种群规模与迭代次数可以提高求解精度，但也会增加计算时间，本文模型求解相对简单，使用经验值，设置初始种群规模数值为200~500，迭代次数为100~500.

步骤2：染色体编码与种群初始化.将需要求解的参数进行编码，生成随机初始解，采用实数编码，编码的长度是交叉口的相位数，每个基因分别表示不同相位的有效绿灯时间，编码产生的有效绿灯时间受到合理绿灯时长的约束，介于最短绿灯时间与最长绿灯时间之间.

步骤3：构建适应度函数.以机动车车均延误、行人人均延误、停车率最小为优化目标构建适应度函数，计算每个个体的适应度，判断其优劣.

步骤4：选择.使用精英保留策略以及轮盘赌策略进行选择.精英保留策略可以防止交叉和变异时将原本最优的精英个体破坏，将每次迭代中的最优值记录下来，并替换适应度值最小的个体.优化程度高的方案被选择的概率更高.

步骤5：交叉.交叉是两个个体通过线性组合而产生新染色体的方法.能使子代从父代获得优良基因，采取实数交叉法，设置交叉概率为0.80~0.98.若第α个染色体aα和第β个染色体aβ在第γ位交叉，交叉操作方法为

式中：aαγ、aβγ分别为aα和aβ在第γ 位的基因；τ为二元取值的随机数，取值为1 时表示进行交叉，取值为0 时不进行交叉.

步骤6：变异.变异可以保持种群多样性，一定程度上避免搜索陷入局部最优.同1 个体的1 个或多个基因均能发生变异，变异概率的大小影响算法的收敛速度，一般取0.002~0.020.对基因aγ的变异操作为

式中：f(δ)=R(1-δ/δmax)2；δmax为最大迭代次数；δ为当前迭代次数；amax(amin)为基因的上（下）限；r、R均为［0，1］之间的随机数.

当迭代次数达到预设的最大次数δmax后便停止运算.

3.2 权重体系的构建

使用两种权重体系，体系1 使用带精英策略的快速非支配遗传算法求解关于3 项指标的Pareto 最优解集，再利用变异系数法得到一组将所有指标设为同一优先级的权重；体系2 利用指标系数法得到一组优先考虑机动车通行效率的权重.

3.2.1 变异系数法

变异系数是样本数据标准差与平均数的比值，反映样本在单位均值上的离散程度，以各项指标数据为样本，可以较为客观地赋权.第m项指标的变异系数vm为

式中：σm为第m项指标的标准差；xˉm为第m项指标的样本均值.

指标中在单位均值意义上离散程度越高，表明其差别越大，可优化的空间也越大，故其在优化目标中所占据的权重应当较大，各项指标的权重wm为

3.2.2 指标系数法

交叉口信号控制方案应适应交通量的变化，平峰时段应侧重减少机动车与行人的冲突，高峰时段则应侧重减少平均延误与停车次数以提高交叉口整体通行效率.各项指标系数的计算参考文献［23］.

1） 机动车与行人延误指标系数.

通常机动车或行人的流量越大，其延误时间也越大，因此根据各自交通流量比对整体延误系数进行分配，第i相位机动车延误指标系数k1i与第i相位行人延误指标系数k2i分别为

式中：si为第i相位的车道最小饱和流量；yi为第i相位的机动车流量比，zi为第i相位人行道交通流量比.

2） 停车率指标系数.

机动车停车次数直接影响车辆延误，其系数与延误系数相似，停车率指标系数为

3） 指标系数归一化处理.

3.3 多目标函数加权归一化处理

多目标函数单位量纲不同，不能简单相加减，需使用隶属度函数归一化处理，利用线性加权后再求和的方法转化为单目标函数，再对每个目标通过变异系数法或指标系数法赋予权重.

使用遗传算法求解3 个目标在约束条件下的最大值和最小值，目标Am（m=1~3）的隶属度函数为

使用两组权重对多目标进行线性加权，线性归一化后的单目标函数为

式中：w1、w2、w3分别为机动车车均延误、行人人均延误、停车率的权重.

4 案例分析

4.1 案例交叉口基本信息

选取北京市知春路与科学院南路交叉口为研究对象.此交叉口为四相位的信控交叉口，4 个方向均有较多机动车进出口道，其中东、西、南、北向分别有7、8、5、4 条机动车进出口车道.4 个方向均有左转待行区，假设该交叉口为单点控制的信号交叉口，交叉口渠化见图2.

图2 案例交叉口渠化示意图Fig.2 Schematic of the channelization at the sample intersection

交通调查时，取60 min 的交通流量数据，每5 min 为1 个时段，共得到12 个时段.调查高峰时段的行人流量，用以计算行人延误.

4.2 求解结果

4.2.1 动态相位方案选择

根据左转车通行能力计算方法，基于每个时段的交通流量，计算案例交叉口4 个方向的左转车通行能力， 判断该组方向是否需要设置左转保护相位，得出方案：1~8 时段采用二相位；9~11 时段采用三相位；第12 时段采用四相位.随着交通流量增加，以及左转与直行方向的车流特征变化，相位方案动态变化，相位在二相位、三相位、四相位中进行选择.

计算各进口方向的饱和流率时，需使用车道宽度、大车、左转车流校正系数等进行修正，结果见表2.在不设置左转保护相位时，各进口的饱和流率应考虑直行车与对向左转车之间的冲突，其饱和流率会小于设置左转保护相位的情况.

表2 修正后饱和流率Tab.2 Corrected saturation flow ratepcu/h

4.2.2 单一目标在约束条件下的最值

在Matlab R2017a 运行环境下，编写遗传算法，求解各时段中每1 个目标在其约束条件下的最大值与最小值，用于后续步骤的线性归一化.

运行10 次程序，避免求最值时陷入局部最优，记录最终取得的机动车车均延误、行人人均延误和停车率的最大值与最小值，然后利用式（33）对这3 个指标进行归一化处理.

4.2.3 权重计算结果

基于本文采用的权重评价体系，得到2 组权重.使用带精英策略的快速非支配排序遗传算法对交叉口信号配时参数进行求解，基于每1 个时段的交通量获得12 个Pareto 最优解集，计算得到变异系数，再对其进行归一化，得到第1 组权重.根据机动车与行人的流量比、各车道及人行道的饱和流率，得到机动车和行人的延误指标系数、停车率指标系数，将以上提到的各指标系数归一化处理，得到第2 组权重，两组权重见表3.

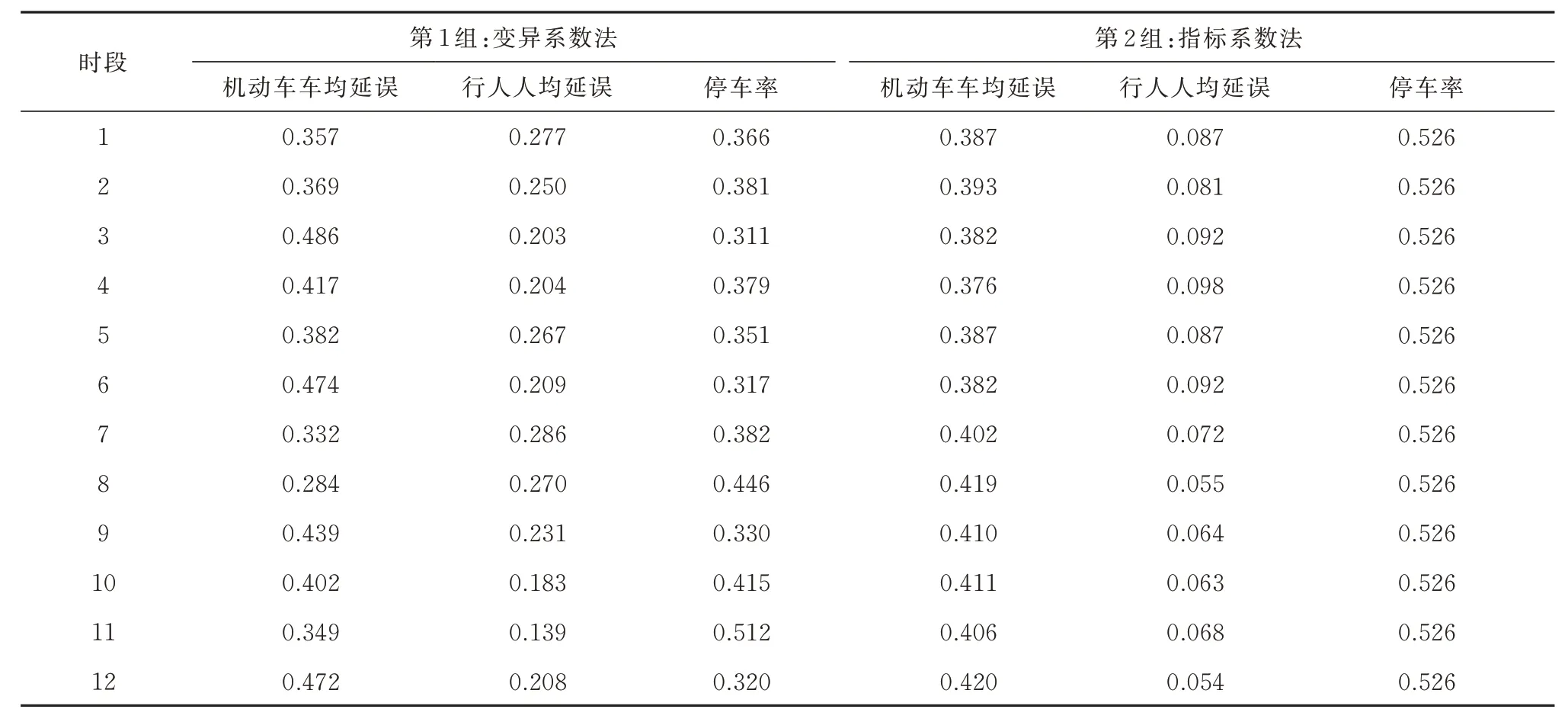
表3 用于多目标函数线性归一化的两组权重Tab.3 Two sets of weights for linear normalization of multi-objective functions

4.2.4 信号配时

将多目标函数中得到的单一目标的适应度进行加权归一化处理，将其转化为单目标函数，使用遗传算法求解最优配时.将种群规模设置为300，根据求解参数数量的多少，将二相位的迭代次数设置为300 代，三相位和四相位迭代次数设置为400 代，变异概率为0.2，交叉概率为0.8.第1 组权重下最优值的收敛曲线见图3.由图3 可知，平均适应度均在最大迭代次数内接近最优.

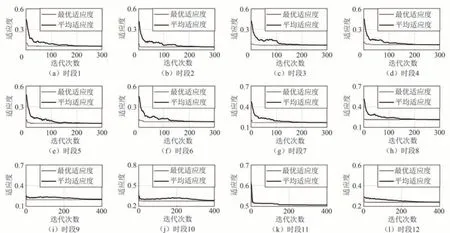
图3 第1 组权重下多目标函数的收敛曲线Fig.3 Convergence curves of multi-objective function under the first set of weights

各相位的绿灯时长、周期时长以及3 项交通运行指标的求解结果见表4.在表4 中：①时段1~时段8 均为二相位，时段9~时段11 为三相位，时段12 为四相位，随着车流量的增加以及交通流特征的变化，交叉口最优相位控制方案由二相位变为三相位，最后变为四相位，实现了动态相位控制方案.②第1 组的配时优化使用的是变异系数法得到的权重，第2 组配时优化使用的是延误指标系数法得到的权重.因为第2 组权重优先考虑了机动车延误以及停车率两个指标，所以第2 组的优化结果中，停车率普遍更小，而行人延误普遍更大.

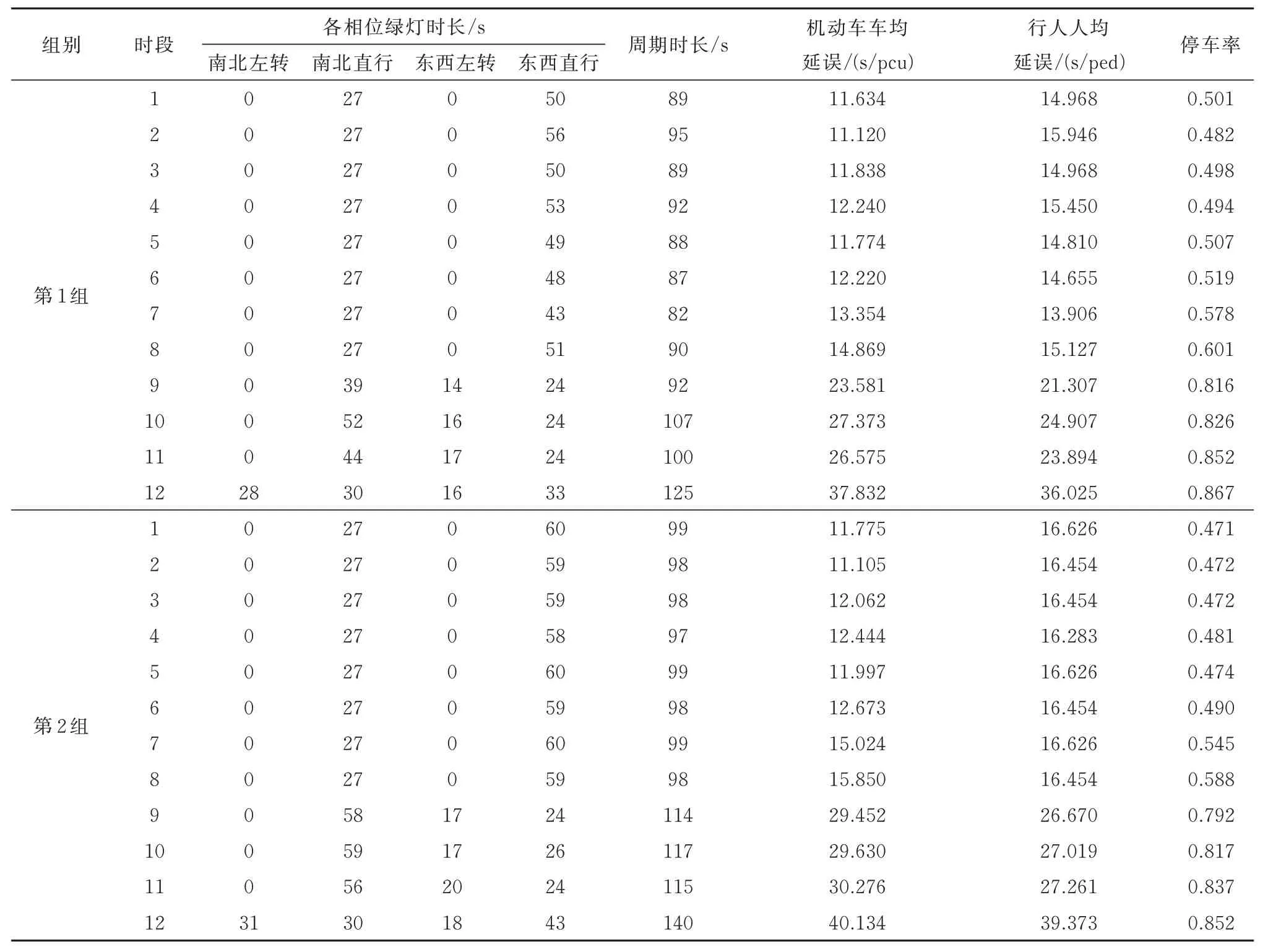
表4 使用两种权重得到的最优配时Tab.4 Optimal timing obtained using two sets of weights

对比优化后的信号控制方案与原方案下的交通运行指标，结果见表5.若该交叉口使用原四相位方案，其在交通量较小的平峰时段，由于相位切换频繁，周期较长，导致固定延误较大，信号控制方案与交通流特征不匹配.若采用动态相位控制方案，在其平峰时段减少相位，进而减少相位损失时间和绿灯间隔时间，可以极大降低机动车车均延误、行人人均延误以及停车率.交通量较小的时段采用二相位控制优化效果明显.

由表5 可知：①两组信号配时方案下，前8 个时段交通量较低，采用了二相位控制，各时段至少能减少58.18%的车均延误、54.86%的行人人均延误以及22.75%的停车率.②时段9~时段11 为三相位，各指标的优化效果也比较显著.③对比原配时和第12 时段的优化结果，发现同样是采用四相位方案.在第1 组权重指标下机动车车均延误、行人人均延误、停车率均能够小幅度优化；在第2 组权重下，由于停车率的优化权重更大，其优化效果较为明显，而机动车车均延误、行人人均延误则没有优化，这主要是因为新方案和原方案均为四相位，相位方案设置差异不大导致的.基于第1 组权重优化，信号配时在四相位时也能在一定程度上改善交叉口的运行指标，体现了优化方法的可行性.

4.2.5 Vissim 仿真

使用AutoCAD 进行绘图，通过对交叉口实地调查以及卫星全景图的观测，获取数据进行绘图，得到知春路-科学院南路交叉口示意如图4 所示.绘图完毕后，在Vissim 8 中搭建仿真模型，选取第1 时段（二相位）、第9 时段（三相位）、第12 时段（四相位）的交通量，设置车流量、车流比例、饱和流率等各类参数，根据案例求解结果设置信号配时方案以及原配时方案，完成模型搭建.

图4 Vissim 仿真运行Fig.4 Vissim simulation operation

设置检测器对各交通运行指标进行检测，仿真运行即可得到相应检测数据.在每1 个时段下均使用原配时与优化后配时的数据进行600 s 的仿真，输出优化前后的车均延误、人均延误、停车率等评价指标，如表6 所示.由表6 可知，在第1 时段若采用二相位信号配时，可以减少机动车车均延误65.67%、行人人均延误59.18%、停车率38.59%.

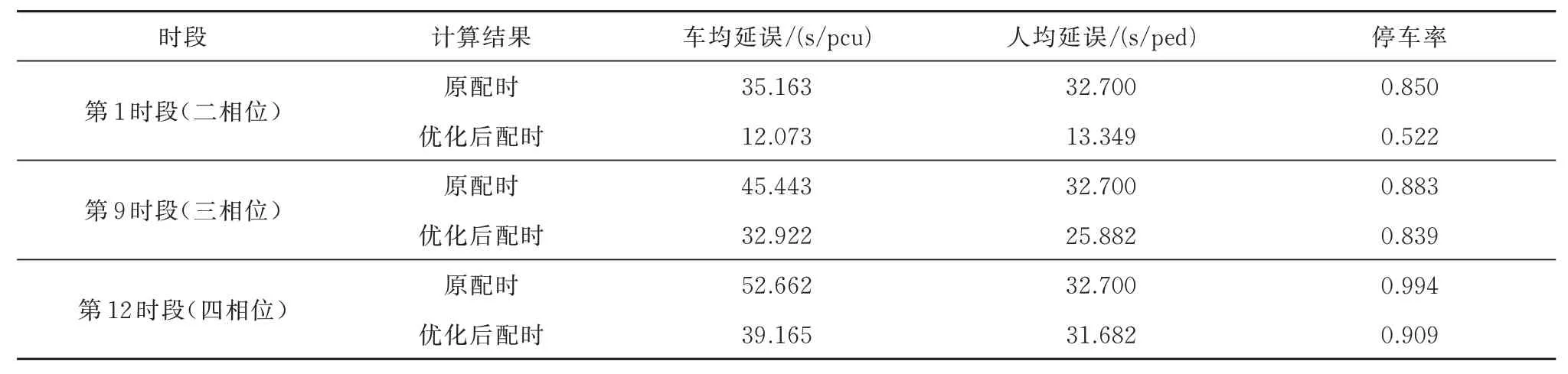
表6 交通运行指标仿真结果对比Tab.6 Comparison of simulation results regarding traffic operation indicators

5 结论

1） 使用传统的二相位、三相位和四相位建立相位库，参考可穿越间隙理论建立车辆在非左转保护相位下通过交叉口的模型，计算考虑冲突条件下的左转车通行能力，以此作为1 种相位控制方案的定量选择依据.

2） 以机动车车均延误、行人人均延误、停车率为优化目标构建多目标信号配时优化模型，建立两种权重评价体系，将多目标模型转化为单目标模型，使用遗传算法求解得到最佳绿灯时长.

3） 案例分析结果表明，若在交通流量较小时段采用二相位控制，能减少58.18% 的车均延误、54.86%的行人人均延误以及22.75%的停车率.交通量较大时采用四相位控制方案，应用遗传算法求解信号配时也能在一定程度上取得优化效果.使用Vissim 构建案例交叉口仿真平台，验证信号配时优化模型的有效性.模型求解结果与仿真结果均表明动态相位方法能够减少机动车延误与停车率，减少行人延误，提高交叉口整体通行效率.

本文还存在一些需要继续深入完善的地方，如优化目标的选取，从时空资源同步优化角度探讨信号控制与渠化设计的协同优化方法等.在应用上，考虑到动态相位研究目前主要是理论探讨居多，在应用层面还未普及，在推广使用时可能会存在一定风险，如人们不熟悉相位变化顺序，可能按照习惯判断红绿灯变化等.对此，建议辅以其他措施进行安全提醒，如可以通过提早路标提示、灯色变化前闪烁等方法降低风险.