考虑磁芯饱和的扼流变压器非线性模型
崔 勇, 杨晓凡, 谢路雨
(北京交通大学 电子信息工程学院,北京 100044)
随着铁路列车速度的提高,牵引电流增大,轨道电路所处的电磁环境也越来越复杂.同时,在铁路信号系统各基础设备中,钢轨是列车牵引电流回流的通路,所以轨道电路会不可避免地受到列车牵引电流干扰,尤其是不平衡牵引电流,易使轨道电路出现分路不良或“红光带”故障[1].而扼流变压器作为25 Hz 相敏轨道电路中强电与弱电的连接枢纽,更易受到电磁干扰.
目前对于扼流变压器模型的研究主要是建立等效电路模型,而对扼流变压器的磁芯饱和特性研究较少.文献[2-4]建立了扼流变压器传统等效电路模型,分析了扼流变压器在地磁感应电流、牵引电流和直流等因素干扰下的工作特性.但这些模型的适用范围小、计算量大,且没有考虑扼流变压器的非线性特性.文献[5]采用数值分析方法建立了扼流变压器的非线性模型,但是该模型推导复杂,计算十分繁琐.
上述研究主要针对扼流变压器的四端网模型,即设定扼流变压器工作在线性区,通过传统的等效电路模型建立扼流变压器的四端网模型,然后在轨道电路模型中进行串联.然而扼流变压器铁芯由硅钢片导磁材料构成,在实际应用中具有磁滞性和饱和性,且扼流变压器往往工作在拐点,不平衡牵引电流、直流干扰会对扼流变压器的工作点产生影响,此时扼流变压器可能会产生磁芯饱和,引起扼流变压器传输阻抗的下降,从而与工作在线性区的传输阻抗特性存在较大差异.
为了解决上述问题,本文采用JA 理论模拟磁滞回线[6-8],结合文献[9]提出的传统等效电路模型,提出了一种考虑磁饱和特性的扼流变压器非线性电路模型.模型建立过程中,采用PSO 算法[10]提取JA 磁滞模型参数,以及能量计算法[11]计算扼流变压器等效电路中的漏电感和漏电容,建立扼流变压器非线性电路模型;并运用励磁涌流理论[12]对建立的非线性电路模型进行瞬态分析.与传统的线性四端网模型相比,本文模型可以反映扼流变压器非线性区的输入输出特性和磁芯饱和情况;与Pspice模型相比,本文模型可实时求解磁芯磁滞回线,并应用于实际现场中的扼流变压器工作状态监测与故障分析.
1 模型建立
以25 Hz 相敏轨道电路的BE1-400/25 型扼流变压器为研究对象,其接线图如图1 所示,牵引线圈分为上下两部分,由2 个8 匝的线圈N1组成,牵引电流iA、iB分别由牵引线圈的两端流入,由中点流出.信号线圈N2由48 匝的线圈组成,变比为1∶3.当牵引电流平衡时,两线圈中的电流大小相等,方向相反,两个线圈所产生的磁通相互抵消;牵引线圈上的信号电流i1由端子1 流入、由端子2 流出,i2为信号线圈上的信号电流,牵引线圈与信号线圈形成变压器.根据扼流变压器的结构,传统的电路模型为如图2所示的T 型等效电路模型.其中,ZL为原边漏阻抗,Rm为铁耗等效电阻,Lm为励磁电感,L3为二次侧线圈电感,T为理想变压器.

图1 扼流变压器电气接线图Fig.1 Electrical wiring diagram of choke transformer

图2 扼流变压器传统电路模型Fig.2 Traditional circuit model of choke transformer
扼流变压器工作过程中的电磁环境比较复杂,往往同时存在多种干扰电流,如不平衡牵引电流以及升降弓脉冲等.分布参数和磁芯会产生电磁干扰通道和影响阻抗.因此本文在传统扼流变压器电路模型的基础上建立考虑分布参数和磁芯的非线性扼流变压器模型,如图3 所示.其中,R1、L1、C1分别为原边绕组的损耗电阻、漏电感和分布电容,R2、L2、C2分别为副边绕组的损耗电阻、漏电感和分布电容,C12为原边绕组和副边绕组之间的分布电容,Lm(i)为考虑磁芯磁滞效应时的励磁电感,U1为一次侧电压,U2为二次侧电压.

图3 非线性扼流变压器模型Fig.3 Nonlinear choke transformer model
1.1 分布参数提取
扼流变压器在实际的工作过程中,有一小部分磁通是以空气作为磁路耦合到变压器副边绕组,由此便产生了扼流变压器的漏感[13].
扼流变压器绕组内漏磁场以纵向漏磁场为主,且纵向漏磁密度一般按照梯形规律分布[14],如图4所示,其中,B表示绕组间漏磁的磁感应强度,Bm为绕组间漏磁最大值.

图4 绕组间漏磁的梯形分布Fig.4 Trapezoidal distribution of magnetic flux leakage between windings
假设绕组长度为h,原边绕组和副边绕组的厚度分别为d1、d2,绝缘间隙为d12,可得原边绕组层中的磁场强度H1、绝缘间隙中的磁场强度H12和副边绕组层中的磁场强度H2分别为
式中:N1、i1分别为原边绕组的匝数、电流,N2、i2分别为副边绕组的匝数、电流;l为绕组层的厚度.假设绕组的平均半径为r,总的漏磁能W为
即
式中:μ0为真空磁导率.
根据能量关系,可得原边绕组漏感L1和副边绕组漏感L2分别为
同理,分布电容也采用同样的方法求解.绕组间的结构及电压分布如图5 所示,其中层间距离为d.绕组间的电压与绕组的长度位置呈线性关系,可得绕组间电压U的表达式为

图5 绕组结构及电压分布Fig.5 Winding structure and voltage distribution
式中:U0、Uh分别是绕组始端x=0 处和终端x=h处的电位差,当绕组为折叠式时,U0=Uh;当绕组为U型时,U0=0.
同理可得两绕组间的电场能Wc为
即
式中:ε0、εr分别是真空电容率和相对介电系数.
则绕组层间的分布电容C为
1.2 JA 磁滞模型
BE1-400/25 型扼流变压器铁芯开气隙为0.2 mm[15].根据磁路中磁动势F与磁阻R的关系,可得扼流变压器的励磁电感Lm为
式中:S为铁芯有效截面积;Rc为铁芯磁阻;Rg为气隙磁阻;lc为磁芯平均磁路长度;lg为气隙长度;μr为铁芯相对磁导率.
由式(12)可得,当扼流变压器工作在线性区时,铁芯磁阻远小于气隙磁阻,电感由气隙磁阻决定,因而励磁电感可以近似等效为定值.当扼流变压器磁芯饱和时,相对磁导率μr变得很小,则会导致励磁电感值很小,此时近似等效已不再适用.因此,有必要对扼流变压器的磁滞回线进行研究,以表征其非线性工作特性.
1.2.1 静态JA 磁滞模型
根据磁畴理论[14]可得实际磁化强度M、无磁滞磁化强度Man、不可逆磁化强度Mirr和可逆磁化强度Mrev的关系分别为
式中:c为可逆磁化系数,表示实际磁化强度M中可逆磁化强度Mrev的占比,取值范围为0~1.
无磁滞磁化强度Man的计算式为
式中:Ms为饱和磁化强度;a为无磁滞磁化曲线的形状参数;α为磁畴间耦合场平均大小;H为磁场强度;He为有效磁场强度且满足
根据能量守恒原理可得到静态磁化过程能量守恒的方程式为
式中:k为不可逆磁化损耗系数;δ为表示磁场变化的方向系数;δM为表示磁化强度的方向系数,作用为避免局部磁滞回线非物理解的出现,表达式为
对式(13)、式(14)和式(16)、式(17)化简,并代入式(18),可得JA 模型磁化强度的微分表达式为
通过对JA 静态磁滞模型的Ms、k、c、a、α五个参数求解,即可得到JA 静态磁滞模型磁芯对应的磁滞回线.
1.2.2 动态JA 磁滞模型
静态JA 磁滞模型只能反映与频率无关的磁滞损耗,因此还需建立可以表征磁芯交流磁化特性的动态JA 磁滞模型.
根据Bertotti 铁芯损耗分离理论,铁芯损耗可分解成3 部分[16],表达式为
式中:Wh为铁芯损耗;We为涡流损耗;Wa为异常损耗,表达式分别为
式中:kc为涡流损耗系数;ka为异常损耗系数.
与静态JA 磁滞模型同理,可得到动态磁化过程中的能量守恒方程式为
对式(23)两端的He进行微分,然后引入以磁感应强度为输入的微分方程,化简得JA 动态模型磁化强度的微分表达式为
动态JA 模型在静态模型的基础上增加了kc和ka两个参数,通过7 个参数来描述磁芯对应的磁滞回线.
2 算法介绍
2.1 JA 模型的参数辨识
本文应用粒子群算法(Particle Swarm Optimization,PSO),利用Matlab 编程实现对JA 磁滞模型的参数辨识,实际上就是求解PSO 目标函数的最小值问题.因此,求解JA 磁滞模型参数时的目标函数可表示为
式中:m为实验数据的个数;Bexp(i)为磁感应强度B的实测值;Bcal(i)为磁感应强度B的计算值.
在算法寻优的过程中,以最小化磁感应强度实测值和计算值之间的误差为目标,进行全局搜索获得JA 磁滞模型参数的最优解.
2.2 励磁涌流分析
在铁芯磁通达到饱和时,若磁通发生微小变化,则励磁电流上会有巨大的变化,变压器一次侧会出现数值很大的暂态电流,即为励磁涌流.因此只有研究励磁涌流的产生机理,才能更深入地了解扼流变压器在磁芯饱和时的输入输出特性,为轨道电路的安全、正常工作提供理论基础和保障.根据励磁涌流理论[14],励磁电流i与磁通Φ的关系曲线如图6所示.

图6 磁通与励磁电流关系图Fig.6 Relationship between magnetic flux and excitation current
由图6 可知,随着磁通的增大,当磁通量超过饱和磁通时,变压器铁芯将会饱和,而励磁电流将会发生畸变产生励磁涌流.
根据麦克斯韦方程中的安培环路定律及磁通表达式,即
式中:N表示线圈匝数;H、l分别表示磁场强度和平均磁路长度.化简可得励磁涌流与磁通的关系为
式中:μ表示铁芯磁导率.因此,利用JA 模型求解磁化曲线、即BH 曲线,可对扼流变压器励磁涌流分析,并通过励磁电流的波形来判断扼流变压器磁芯是否饱和.
3 仿真分析
3.1 JA 模型参数辨识结果
利用动态JA 磁滞模型,编程计算扼流变压器铁芯的JA 磁滞模型参数,并将辨识得到的磁化曲线与实测磁化曲线进行对比,进而验证PSO 计算JA 磁滞模型参数的可行性.扼流变压器的硅钢片型号为30Q120,JA 磁滞模型辨识时设置的实验数据如下:PSO 参数中,根据经验值并结合辨识效果,最终设定粒子群的种群规模n为60,最大迭代次数tk为200,学习因子c1=1.3,c2=1.7,惯性因子w采用时变权重,范围设为0.1~0.9.根据JA 磁滞模型参数的物理意义,结合实测初始磁化曲线确定PSO 中JA磁滞模型7 个参数的搜索范围如表1 所示,其中Htip和Mtip分别为磁场强度顶点值和磁化强度顶点值.以动态JA 磁滞模型的参数辨识为例,辨识结果如表1 所示,辨识过程中,对应的误差迭代曲线如图7所示.

表1 JA 模型各参数搜索范围与辨识结果Tab.1 Search range and identification results of each parameter for the JA model
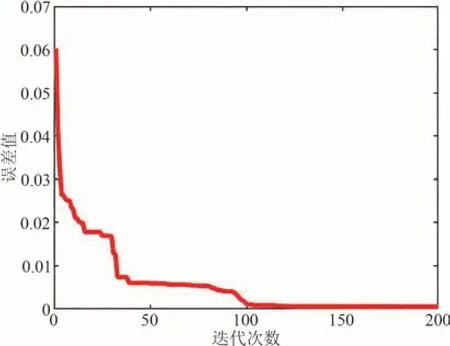
图7 目标函数误差迭代变化曲线Fig.7 Iterative variation curve of objective function error
根据表1 的参数辨识结果可以看出,参数辨识结果符合理论设定范围,且从图7 可知,迭代计算到100 次左右时,最优个体适应值已达到0.000 25,这表明此时得到的JA 磁滞回线参数与实验曲线的参数基本吻合,本文模型及算法计算的辨识参数具有有效性.将利用JA 磁滞模型辨识参数仿真计算的磁化曲线与文献[17]中实测的磁化曲线数据进行对比,结果如图8 所示.

图8 初始磁化曲线实验结果对比图Fig.8 Comparison graph of experimental results for initial magnetization curve
由图8 可知,在初始磁化曲线的计算中,仿真计算结果和实测结果在整个磁场强度范围都能非常好的吻合,验证了PSO 在JA 磁滞模型参数辨识时具有较好精确性.最后,对比根据辨识参数得到的扼流变压器动态磁滞回线和静态磁滞回线,如图9所示.
由图9 可知,在静态磁滞回线和动态磁滞回线的计算中,整个磁场强度范围内的2 个计算结果整体趋势都能较好的吻合;磁芯在交流磁化中的动态磁滞回线相较于在静态磁滞回线中的磁滞损耗有所增大,这是由于采用静态模型进行求解时,模型中只考虑了与频率无关的磁滞损耗,没有考虑交流磁化影响下的涡流损耗和异常损耗,所以静态磁滞回线略小于动态磁滞回线,与理论分析相符.
3.2 扼流变压器非线性模型的分析验证
依据三电容模型仿真计算扼流变压器的分布参数,并根据扼流变压器的实际结构运用Maxwell 有限元软件进行建模与仿真,对模型的计算值进行验证.扼流变压器原边绕组采用截面积为46.2 mm2的双玻璃丝包扁铜线绕制而成,绕制方式为立绕式,绝缘厚度为0.4 mm;副边绕组采用直径为2 mm2的双玻璃丝包圆铜线绕制而成,绝缘厚度为0.25 mm;绕组层间的绝缘间隙为0.5 mm,绕组的平均半径为49 mm.铁芯由2 个32 mm×64 mm×160 mm 的CD型铁芯组成.在Maxwell 建立扼流变压器的仿真模型,如图10 所示.

图10 扼流变压器的3 维模型图Fig.10 3D model diagram of choke transformer
设置相应的边界条件和激励,利用场求解器得到分布电容和漏感表征的总能量,进而求解出扼流变压器分布电容和漏感的仿真值.仿真结果与理论计算值如表2 所示.

表2 扼流变压器分布参数计算结果对比Tab.2 Comparison of calculation results for distribution parameters in choke transformer
由表2 可知,仿真值与理论计算值比较吻合,验证了模型的有效性.同时由于在Maxwell 中仿真时将扼流变压器绕组等效成了理想的圆形,且能量场的能量值数量级较小,读数存在一定的误差,因此,理论值与仿真值间存在一定的误差.
根据模型参数仿真计算调整状态下接收端扼流变压器正常工作时两端的电压和电流.仿真参数如下:信号频率为25 Hz,牵引线圈的电压和电流分别为Uj=0.435 6∠72.7°和Ij=0.823 1∠41.32°;信号线圈的电压和电流分别为Ubej=1.300 95∠73.23°和Ibej=0.213∠65.07°.利用扼流变压器非线性模型求解BH 曲线及其两端的电压电流曲线.在Pspice 中搭建接收端扼流变压器非线性仿真模型,仿真参数与上述电压电流仿真参数一致.将计算结果与仿真结果进行对比,如图11 所示.

图11 正常工作时计算结果与Pspice 仿真结果对比Fig.11 Comparison of calculation and Pspice simulation results during normal operation
由图11 可知,Pspice 的仿真结果和本文模型的结果吻合精度较高,仿真的扼流变压器的一次侧、二次侧电流幅值分别为0.831 A、0.253 6 A,仿真计算的二次侧电压幅值为1.219 V,与四端网模型的计算结果基本吻合,验证了模型和仿真结果的正确性.从图11(a)可知,扼流变压器在轨道电路中正常工作时磁芯的磁感应强度远小于在磁芯饱和时的磁感应强度.此时,扼流变压器工作在线性区,磁滞回线为交流磁滞回环.同时对应的励磁电流波形为正负对称的正弦波.改变扼流变压器一次侧的激励电压幅值和频率,仿真牵引回流令其磁芯达到饱和状态,仿真参数为50 V,频率为50 Hz,其余参数与正常工作状态时相同.对比结果如图12 所示.

图12 磁芯饱和时计算结果与Pspice 仿真结果对比Fig.12 Comparison of calculation and Pspice simulation results when magnetic core is saturated
由图12(a)可知,对比Pspice 仿真结果和本文模型计算结果,此时扼流变压器磁芯饱和,对应的磁滞回线为饱和磁滞回线,且仿真和计算的磁滞回线基本吻合;对应的图12(b)和图12(c)中的饱和一次侧电流和二次侧电压的仿真结果变化趋势也基本吻合,但峰值存在略微的差别.这是由于当扼流变压器磁芯处于深度饱和时,磁滞回线上的微小差别反映在励磁电流上也会存在较大的差距.由于Pspice 仿真结果和JA 磁滞模型对应的磁芯磁滞回线存在微小的差距,所以此时求解得到的励磁电流在幅值上有细微的误差.
由图12(b)可知,励磁电流在0.004 1 s 时突增,发生畸变.根据磁通Φ与励磁涌流的理论分析可知,此时变压器磁芯饱和.对应的二次侧电压在0.004 2 s 时突减;根据式(12)可知,磁芯饱和时相对磁导率突减,进而励磁电感Lm突减,即扼流变压器的传输阻抗大大减小,导致扼流变压器二次侧的电压值也大幅减小,与图12(c)中的仿真结果一致.25 Hz 信号电流对应的二次侧电压如图13 所示.由图13 可知,磁芯饱和时信号线圈的输出电压幅值降为0 V,会引起红光带故障.

图13 磁芯饱和时信号电压结果对比图Fig.13 Comparison of simulation results of signal voltage when magnetic core is saturated
综上可知,磁芯饱和时对于扼流变压器的输出电压及电流有明显影响.对比扼流变压器正常工作及饱和状态的仿真结果表明,当扼流变压器工作在线性区时,BH 曲线没有进入饱和区,励磁电流为正负对称的正弦波;当扼流变压器磁芯饱和工作在非线性区时,BH 曲线进入饱和区,磁滞回线为饱和磁滞回线,励磁电流发生畸变.因此,可以通过扼流变压器原边电流的波形或者磁芯的磁滞回线形状来判断扼流变压器发生故障时磁芯是否饱和,并且指导实际现场中的扼流变压器故障诊断.
4 结论
1)提出一种结合JA 磁滞模型及三电容变压器模型的扼流变压器非线性模型的建模方法,该方法在传统的扼流变压器T 型等效电路模型建模方法上做了进一步的优化,相较于传统的方法,本文模型可应用于扼流变压器磁芯饱和等非线性的问题分析,在饱和机理、磁芯模型的建立以及饱和分析上都有较强的应用性.
2)采用PSO 算法来提取扼流变压器中磁芯的磁滞回线参数,同时运用能量计算法来提取扼流变压器的漏电感和分布电容,这种模型及算法的物理意义明确,便于理解和计算.
3)将仿真的分布电容参数的计算结果与Maxwell 的仿真结果进行对比验证,得出本文模型的方法在提取扼流变压器漏感和分布电容的参数时具有较好的精确性;将非线性扼流变压器模型的求解结果与Pspice 的仿真结果进行对比验证,说明本文的模型及算法可以较准确地分析扼流变压器中磁芯饱和问题.可以通过分析此模型磁芯的实时磁滞回线形状或者扼流变压器原边电流的畸变情况来判断扼流变压器磁芯是否饱和.

