SiC MOSFET 有源驱动电路关断轨迹优化方法

陈月清 ， 郭希铮 ， 部旭聪 ， 郝瑞祥 ， 游小杰，2

（1.北京交通大学 电气工程学院，北京 100044；2.轨道交通安全协同创新中心，北京 100044）

SiC MOSFET 具有高开关速度、低导通损耗和高热导率等优点，已广泛应用于轨道交通、光伏发电、新能源汽车与充电桩等中大功率场合［1］.然而，SiC MOSFET 的快速开关特性使其在开关暂态过程中更易受功率回路的寄生参数影响，过高的漏源极电压变化率dvds/dt和漏极电流变化率did/dt带来了开关瞬态电压电流的振荡和电磁干扰（Electromagnetic Interference，EMI）问题［2］.

优化PCB 布局和功率回路寄生参数，增加RC缓冲电路、驱动电阻或栅源电容等方法可以改善SiC MOSFET 的关断性能.但是抑制EMI 的效果有限，同时会显著增加开关损耗、降低变换器功率密度［3］.

目前，利用有源驱动电路（Active Gate Driver，AGD）改善SiC MOSFET 开关特性受到广泛关注，其基本思想是：将开关暂态细分为多个子阶段，并为特殊子阶段选择不同的驱动电阻、驱动电流或驱动电压，增加额外自由度来动态控制SiC MOSFET 开关过程的电压电流变化率. 例如，文献［3-4］指出，驱动电阻、驱动电压等驱动参数固定的AGD 电路的适用性较差，难以确保SiC MOSFET 工作于电气应力与损耗的优化折衷点.文献［5］通过多级电阻并联，并在不同阶段设定相应优化目标，选择对应的驱动电阻值.文献［6］采用63 对PMOS-NMOS 实现驱动电流的高分辨率控制，并采用粒子群优化算法（Particle Swarm Optimization，PSO），寻求优化驱动参数配置，但所提方法的驱动电路过于复杂，降低了系统可靠性.文献［7］通过调节驱动电压的切换时间来实现电气应力与损耗的优化折衷，但受限于功率放大模块的拓扑，无法调节驱动中间电平值.而文献［8］利用可调线性稳压器（Low Dropout Regulator，LDO）使得驱动中间电平能够根据使用场合灵活设定，并通过改变中间电平值优化调节对应工况下的关断性能改善效果，但是该方法将中间电平作用时间固定在关断漏源极电压上升阶段，导致关断损耗明显增加.文献［9］遍历关断过程的传统驱动给定电压、中间电平电压以及驱动电阻的不同组合，将关断损耗、漏源极电压变化率和漏极电流变化率的Pareto 前沿视为最优解，从而求得对应的优化驱动参数.但上述方法同时会带来开关损耗增加问题，因此电气应力与损耗的优化折衷是目前有源驱动电路设计的难点.

目前已有相关研究对SiC MOSFET 开通过程瞬态特性进行了改善. 文献［10-11］指出，SiC MOSFET 在开通过程可承受的瞬态脉冲电流较大，开通电流尖峰值Ip主要导致开通损耗增加，通常不会对SiC MOSFET 的安全裕度产生影响，即开通暂态无“电流应力”裕度问题.因此，对于开通过程主要优先考虑选择合适的开通驱动电阻以尽可能降低开通损耗Eon［12-13］，从而实现开通过程瞬态特性的改善.然而对于关断过程中SiC MOSFET 的轨迹优化问题，目前缺少公认的优化方法研究.

综上所述，现有的有源驱动电路在大功率应用场合，存在电气应力与损耗难以权衡以及驱动参数优化设计复杂等问题.为此，本文提出一种SiC MOSFET 关断轨迹优化方法，通过解析SiC MOSFET 关断过程，建立关断轨迹预测模型.利用目标函数求解有源驱动关断中间电平的切换电平值和切换作用时间优化值，使得SiC MOSFET 工作在关断电压尖峰与关断损耗的优化折衷点.最后通过实验验证所提方法的有效性和适用性.

1 SiC MOSFET 关断轨迹预测模型

考虑功率回路寄生参数的SiC MOSFET 等效电路模型如图1 所示.图1 中，Q1、Q2为半桥上、下桥臂SiC MOSFET，VDC和CDC分别为直流母线电压和支撑电容，Vgg为有源驱动的给定驱动电压，Lbus和Rbus分别为直流母线的寄生电感和寄生电阻，Lload为建流电感，Rgin和Rgext分别为SiC MOSFET 内部和外部驱动电阻，Cgs、Cgd和Cds分别为栅源极电容、栅漏极电容和漏源极电容，Ld和Ls分别为漏极寄生电感和源极寄生电感.

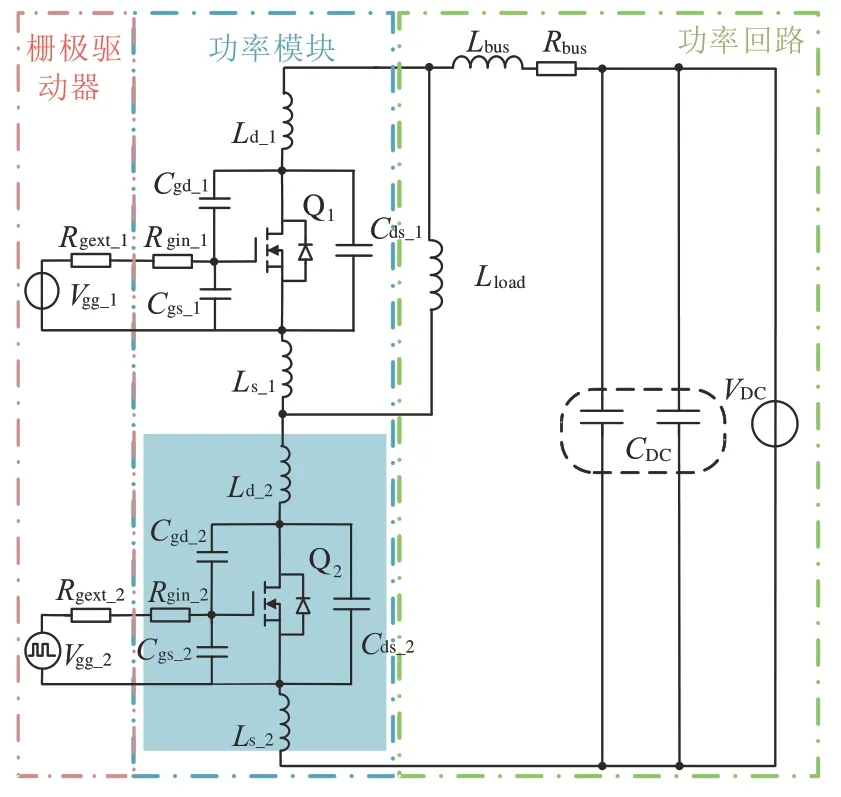
图1 考虑功率回路寄生参数的SiC MOSFET 等效电路模型Fig.1 Equivalent circuit model of SiC MOSFET considering parasitic parameters in the power circuit

输入电容Ciss、转移电容Crss和输出电容Coss分别为

定义主电路集总杂散电感Llump和总驱动电阻Roffg分别为

以下桥臂SiC MOSFET 为分析对象，分析其关断瞬态过程，并基于关断瞬态分析建立SiC MOSFET 的关断轨迹预测模型.关断过程的分析主要关注关断过程的以下特性：关断延迟阶段时间toffd；漏源极电压上升变化率dvds/dt，关断电压尖峰Vp，漏极电流下降变化率did/dt；关断损耗Eoff.

关断瞬态过程分为4 个子阶段，典型波形如图2所示［14］.图2 中，vds、id和vgs分别表示漏源极电压、漏极电流和栅源极电压，vint为切换的中间电平值，tdint表示切换驱动电平为中间电平值的时间，Vth为阈值电压.

图2 SiC MOSFET 关断暂态波形Fig.2 SiC MOSFET turn-off transient waveform

1）关断延迟阶段［t1，t2）.

输入电容Ciss在关断负压VEE作用下，通过驱动电阻放电，直至栅源极电压vgs下降至米勒电压Vmiller，该段时间为关断延迟时间toffd，即

式中：Roffg为总驱动电阻；VCC为开通正压.

2）电压上升阶段［t2，t4）.

栅源极电压vgs保持在米勒电压Vmiller，转移电容Crss通过总驱动电阻Roffg放电，漏源极电压vds的瞬态变化率为

转移电容Crss是随vds变化的非线性电容，可利用datasheet［15］所提供的Crss参数进行分段拟合.［t2，t3）阶段，Crss为nF 级，vds缓慢上升到Vmiller-Vth；［t3，t4）阶段，Crss为pF 级，vds快速上升到母线电压VDC.

定义从0.1 倍母线电压VDC上升到0.9 倍母线电压VDC过程的dvds/dt为vds的平均电压变化率dvds/dtavg，可利用线性损耗模型［8］计算该阶段损耗Eoff，tvr2为

式中：IL1表示负载电流；IL2表示t4时刻漏极电流，具体为

3）电流下降阶段［t4，t5）.

漏极电流id从SiC MOSFET 换流至对管体二极管并快速下降.将该阶段平均电压（Vth+Vmiller）/2 近似代入vgs，得到平均漏极电流变化率did/dt为［7-8］

式中，跨导gfs采用文献［2］所给的线性化跨导公式近似替代.

图3 为在总驱动电阻Roffg为6 Ω 工况下切换中间电平的驱动电流对比图，橙色波形为使用关断负压VEE直接关断不增加中间电平切换的传统驱动（Conventional Gate Driver，CGD）对应的驱动电流，蓝色波形为切换中间电平为0 V 的AGD 对应的驱动电流；①为中间电平切换过程，②为中间电平切换完成后实际作用到SiC MOSFET 的过程.由图3 可知，经过切换过程①的延迟后，AGD 驱动电流下降为对应的驱动电流值，即驱动电流变化量∆ig=0.6 A.相应地，漏极电流变化率did/dt经过延迟才满足式（10）.因此中间电平作用时间影响漏极电流变化率的改善效果.

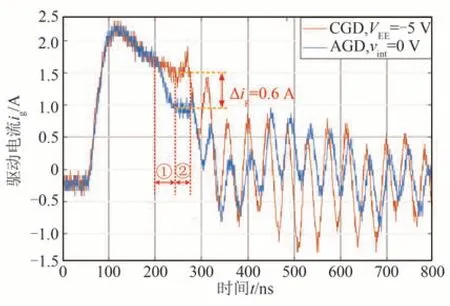
图3 切换中间电平的驱动电流对比Fig.3 Comparison of grid current for switching intermediate level

有源驱动中栅源极电压vgs为变量，导致电流变化率did/dt并非常数，需进一步根据等效电流斜率思路，将有源驱动过程中变化的did/dt近似等效为恒定的平均电流斜率.

结合图2 中时刻的定义，得到等效电流斜率示意图，如图4 所示.图4 中t4为电流开始快速下降的时刻，t1+tdint为加入驱动中间电平的时刻，did/dtVEE为加入中间电平前的漏极电流变化率，did/dtvint为加入中间电平后的电流变化率理论计算值，did/dteq为所求解等效平均电流斜率.根据图4 列写电流IL2等式，即

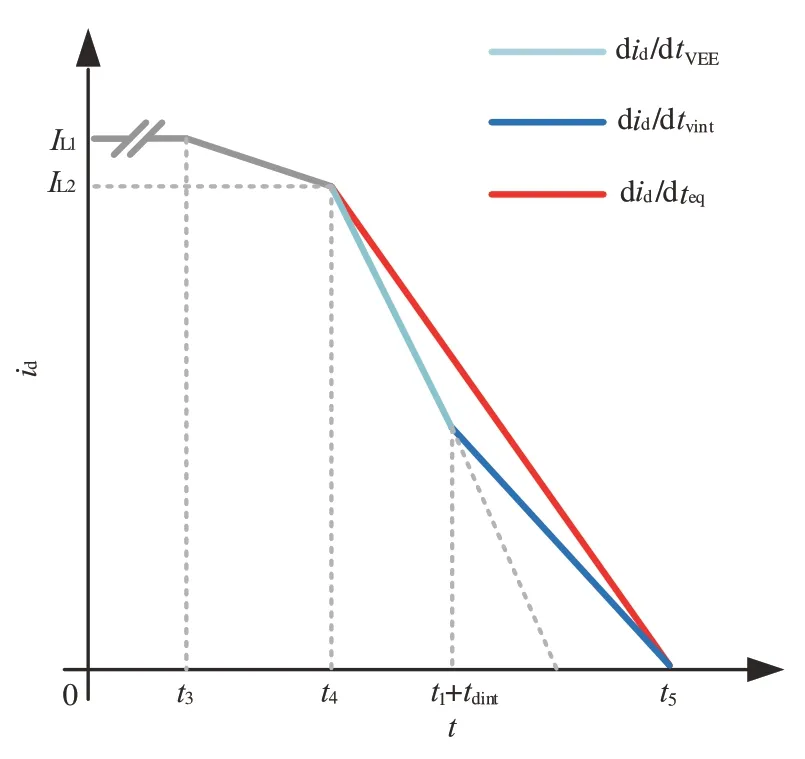
图4 等效电流斜率Fig.4 Equivalent current slope

利用式（11），求解总体电流下降时间为

结合式（11）和式（12），求解得到等效平均电流斜率did/dteq为

did/dteq作用于集总杂散电感Llump，使得漏源极电压产生的关断电压尖峰Vp为

式中，Vos为关断电压过冲值.

进一步求解电流下降阶段损耗Eoff，tcf为

关断总损耗Eoff为电压上升阶段损耗Eoff，tvr2与电流下降阶段损耗Eoff，tcf之和，即

4）振荡衰减阶段［t5，t6）.

漏源极电压vds呈现衰减振荡，具体的衰减阻尼系数ζ和振荡频率f为

通过对SiC MOSFET 关断瞬态过程的分析可知，栅源极电压vgs是影响SiC MOSFET 关断性能的关键因素，调节有源驱动的中间电平可降低电压应力、减小EMI 噪声、改善关断轨迹，但同时也带来损耗增加的问题.不同的中间电平参数设计将直接影响关断性能的优化效果.而有源驱动的中间电平参数包含切换时间tdint和中间电平值vint，增加了优化驱动参数设计的困难.

2 SiC MOSFET 关断轨迹优化方法

2.1 SiC MOSFET 模型参数提取

模 型 以 Infineon 的 SiC MOSFET 模 块FF6MR12KM1P 为例，相关参数可直接从datasheet［15］提取. 表1 为关断轨迹模型需要的SiC MOSFET 模块参数，其中模块杂散电感LsCE=Ld+Ls，输出电容Coss为600 V 母线电压下的平均寄生电容值［16］.非线性电容Crss采用分段函数拟合，拟合结果如图5 所示，具体拟合表达式为

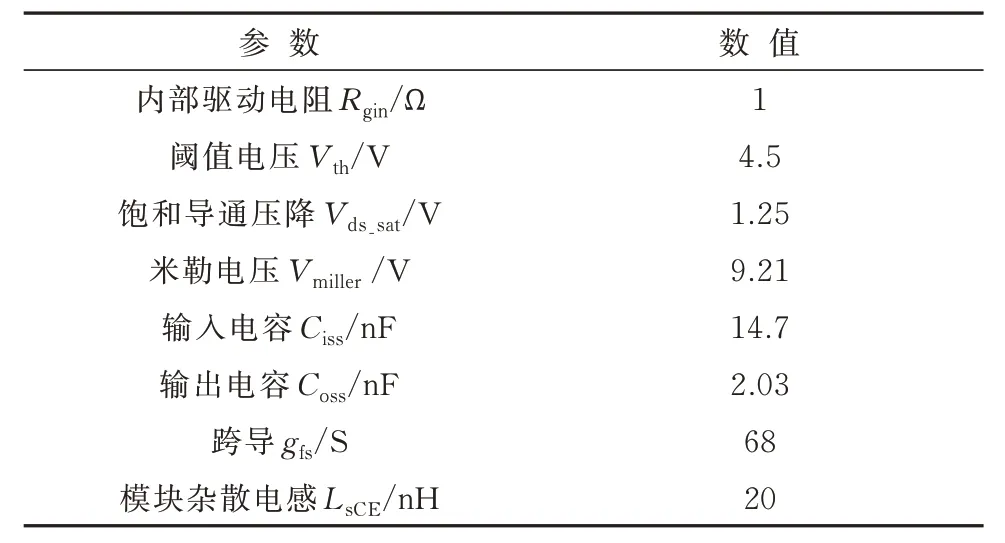
表1 SiC MOSFET 模块参数Tab.1 SiC MOSFET module parameters

图5 转移电容拟合Fig.5 Fitting of transfer capacitance

2.2 基于模型的关断轨迹优化方法

基于对SiC MOSFET 关断瞬态过程的分析可知，关断电压过冲和关断损耗是2 个互相制约的量，需要优化折衷.为寻求关断电压过冲和关断损耗最优折衷点对应的中间电平参数，设置目标函数cost 为

式中：Vos_normal、Eoff_normal表示在传统驱动关断下的漏源极电压的关断过冲以及关断损耗；α、β表示权重系数，α=β=0.5.

由式（20）可知，目标函数由关断电压过冲Vos和关断损耗Eoff组成，由于量纲单位不同且变化区间处于不同的数量级，故利用传统驱动关断下的关断电压过冲以及关断损耗进行归一化处理.可通过求解目标函数cost 的最小值来选取中间电平的优化参数.

图6 为基于目标函数的关断特性优化方法流程图.通过对传统关断瞬态过程的计算，获取关断瞬态不同阶段的持续时间，包括关断延迟时间tdoff、电压上升时间tvr、电流下降时间tif.切换中间电平的时间tdint从tdoff变化至tdoff+tvr+tif，中间电平值vint从传统关断负压-5V 变化至3V.遍历切换中间电平的时间和中间电平值，在对应工况下计算目标函数，获取目标函数最小值对应的优化中间电平参数.

图7 为外部驱动电阻Rgext=5 Ω 时，利用优化方法计算得到的中间电平参数.由图7 可知，中间电平值vint=2.5 V 且中间电平作用时间tdint=170 ns 时，目标函数cost 最小.

3 实验验证

3.1 SiC MOSFET 有源驱动电路及实验设置

图8 为SiC MOSFET 多电平有源驱动电路的总体结构.采用复杂可编程逻辑器件（Complex Programming Logic Device，CPLD）实现电路逻辑控制功能，包含原边CPLD 发出的上下桥臂脉冲信号pwm1 和pwm2 的控制以及副边CPLD 发出的有源驱动中间电平的3 位二进制信息流Ai、Bi、Ci的控制.整体控制逻辑简单，确保了驱动电路的可靠性.

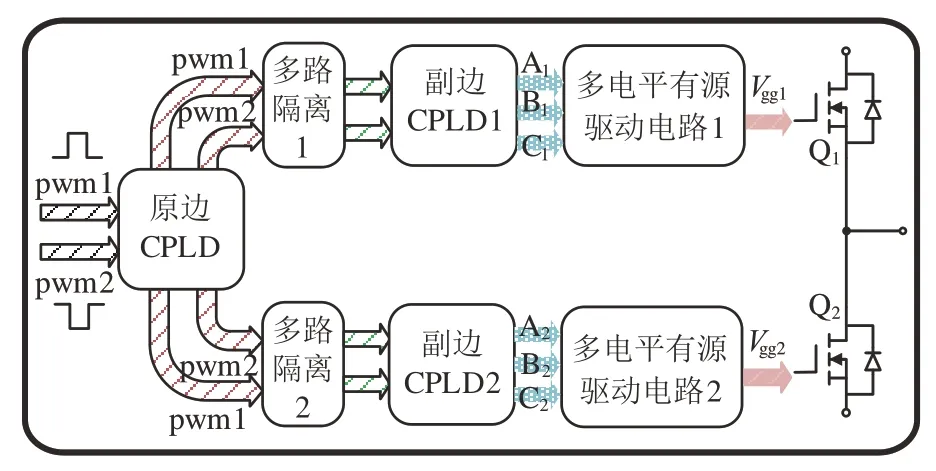
图8 半桥SiC MOSFET 多电平有源驱动电路总体结构Fig.8 Overall structure of multi-level active driving circuit for SiC MOSFET half bridge module

图9 为本文采用的多电平有源驱动电路，该电路由高速模拟开关、电压放大和功率放大3 部分构成.高速模拟开关采用74HC4051，支持8 路模拟电压输入，供电电压为±5 V，可满足SiC MOSFET 有源驱动更多电平数量选择的需求，且传输延迟仅为4 ns，可满足驱动电路的高频应用需求.通过CPLD 在需要切换的时刻输出的3 位二进制信息流，控制高速模拟开关选择对应的输入通道连接至模拟开关输出通道，而不同的输入通道对应着不同的给定驱动电压Vgg，实现中间电平给定电压在对应时刻的切换.

图9 多电平有源驱动电路Fig.9 Design of multi-level active driving circuit

电压放大电路将高速模拟开关的输出电压进行比例放大以满足驱动SiC MOSFET 的电平等级.通过增设相移电容避免反馈网络出现相移导致输出信号振铃.功率放大电路采用三极管M1和M2搭建的互补射极跟随器，可实现开通驱动电阻和关断驱动电阻的独立设置.Vsupply+和Vsupply-分别为图腾柱的正负供电电压，分别为18 V 和-10 V.表2 为多电平有源驱动电路所用的关键元器件型号表.

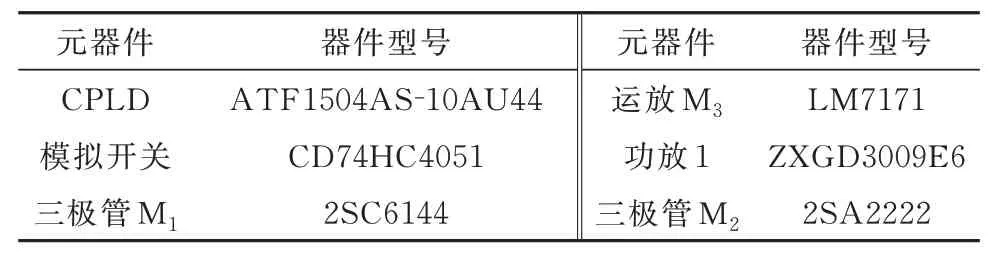
表2 驱动电路关键元器件型号Tab.2 Key component models of the driving circuit

为验证所建模型的准确性及有效性，搭建双脉冲测试（Double Pulse Test， DPT）平台，平台如图10所示，实验参数如表3 所示.

表3 实验参数Tab.3 Experimental parameters

图10 双脉冲测试实验平台Fig.10 Experimental platform for double pulse test

3.2 模型准确性验证

关断过程中重点关注对SiC MOSFET 关断损耗和关断时长有显著影响的前3 个阶段，即关断延迟、电压上升及电流下降过程.表4 为在外部驱动电阻为5 Ω 的不同驱动模式下，模型计算与实验测量的相对误差表，包含关断延迟时间相对误差δtoffd、漏源极电压变化率相对误差δdv/dt、关断电压尖峰相对误差δvp以及关断损耗相对误差δEoff.相对误差δ（x*）为

表4 模型与实验结果的相对误差Tab.4 Relative errors between model and experimental results%

式中：x*为模型计算值；x为实验测量值.

由表4 可知，所建模型计算的关断延迟时间toffd、漏源极电压变化率dvds/dt以及关断电压尖峰Vp与实验结果的相对误差均小于4%，验证了模型在不同驱动模式下均具有较高的准确性；关断损耗相对误差约为10%，主要源于采用线性损耗模型进行简化计算.

图11 为不同驱动模式下所建预测模型计算结果与实验测量结果对比图.由图11 可知，不论是在CGD 模式还是AGD 模式下，所建模型的预测结果与实验结果均具有较高匹配度.但在振荡阶段，模型计算的振荡频率和振荡幅值与实验测量结果不能完全匹配.该部分误差一方面是由于本文重点关注关断过程的前3 个阶段，对振荡阶段进行了简化处理；另一方面，功率回路中寄生参数对振荡阶段有较大的影响，而测量获取的功率回路寄生参数与实际数值存在一定偏差.

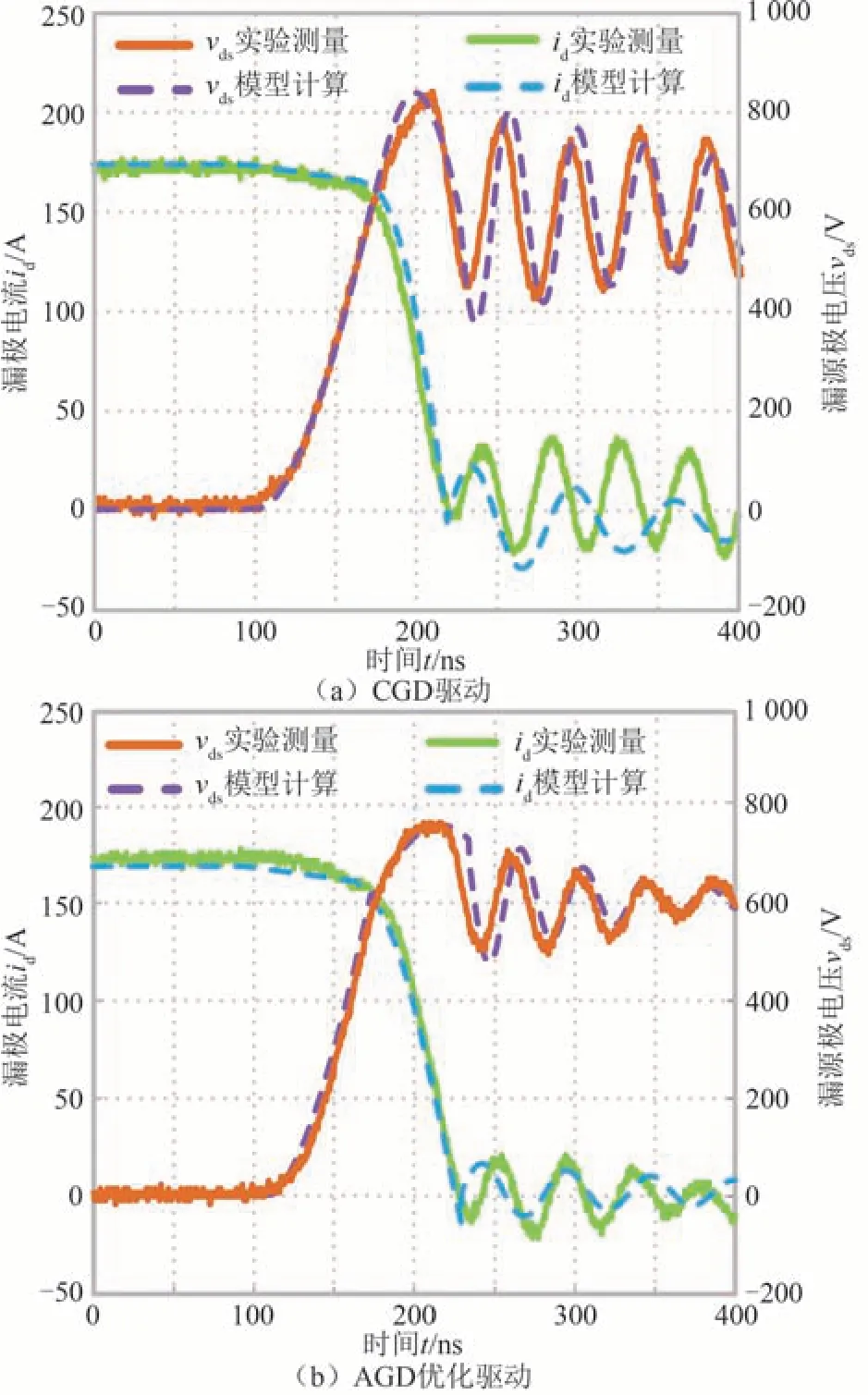
图11 不同驱动模式下模型与实验结果对比Fig.11 Comparison between model and experimental results under different driving modes

3.3 关断轨迹优化方法验证

利用所提关断轨迹优化方法，得到不同负载电流下对应的最优中间电平参数，包含中间电平值vint和切换时间tdint，如图12 所示.由图12 可知，在外部驱动电阻为5 Ω 的情况下，随着负载电流增加，优化中间电平值逐渐增加，且作用时刻提前.这是由于在较小负载电流下，SiC MOSFFET 的关断电压尖峰较小，使用较小的中间电平值可避免产生多余开关损耗；而在较大负载电流下，SiC MOSEFT 关断电压应力增大，需进一步增大中间电平值以有效抑制关断电压尖峰，避免SiC MOSFET 过电压击穿失效.此外随着负载电流增加，优化中间电平的作用时间不断提前，这是由于负载电流增加使得SiC MOSFET 关断过程加快，关断延迟时间和电压上升时间都逐渐减短，故需提前中间电平切换时间tdint以有效抑制关断电压尖峰.

图12 不同负载电流下最优中间电平参数Fig.12 Optimal intermediate level parameters under different load currents

为验证所提SiC MOSFET 关断特性优化方法的有效性，在VDC=600 V、IL1=180 A 工况下，针对5 Ω 外部驱动电阻，实验对比CGD、未优化AGD 以及优化AGD 这3 种驱动模式.不同驱动模式的参数设置如表5 所示.表6 和图13 为不同驱动模式下的关断特性对比.由表6 可知，相比CGD，未优化AGD的关断电压过冲降低了18%，关断损耗增加了3.9%，对应目标函数计算值为0.93；而优化AGD 的关断电压过冲降低了34%，关断损耗增加了6.7%，对应的目标函数为0.86.利用所提优化方法的优化AGD 目标函数值更小，在较小关断损耗增加的前提下，可显著降低关断电压尖峰，改善SiC MOSFET关断特性.

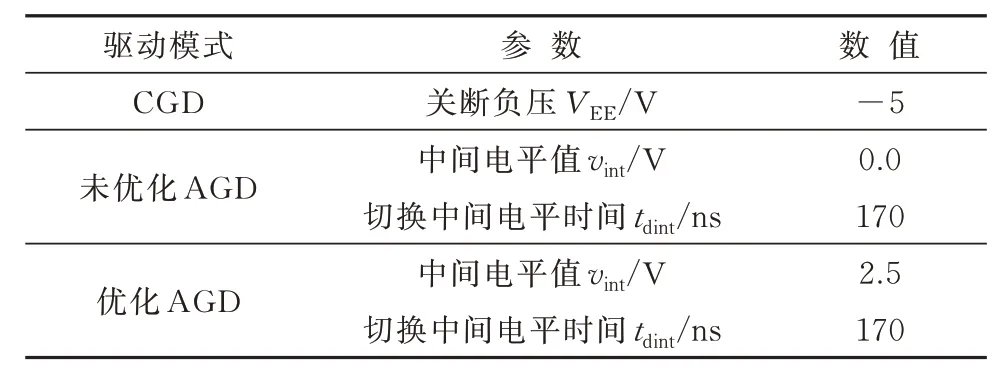
表5 5 Ω 驱动电阻下不同驱动模式的驱动参数Tab.5 Driving parameters for different driving modes under 5 Ω gate resistance

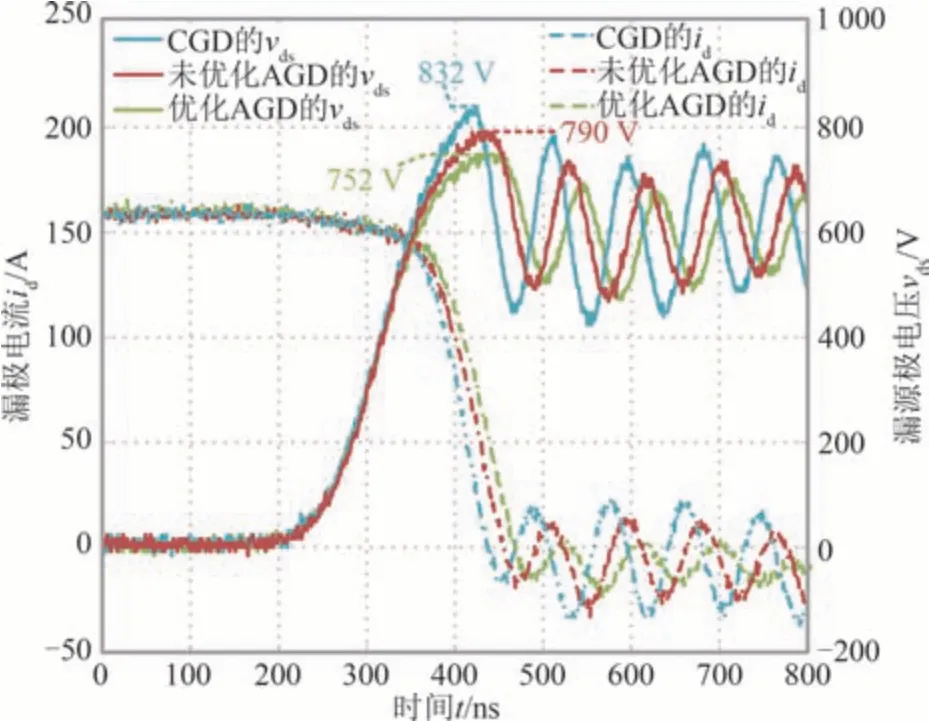
图13 5 Ω 外部驱动电阻下不同驱动模式的关断特性对比Fig.13 Comparison of turn-off characteristics for different driving modes under 5 Ω external gate resistance

图14 为不同驱动模式下漏源极电压vds的频谱分析图.由图14 可知，vds电压振荡均在23 MHz 附近产生尖峰，低频段的幅频曲线基本一致.相比CGD，未优化AGD 的vds频谱幅值降低了4 dB，优化AGD的vds频谱幅值降低了9 dB，说明优化AGD 能够从源头上减小高频EMI.

图14 不同驱动模式下漏源极电压vds频谱分析Fig.14 Spectrum analysis of drain-source voltage vds for different driving modes

3.4 关断轨迹优化方法的适用性验证

为验证所提优化方法及关断轨迹预测模型对驱动电阻的适用性，针对7.5 Ω 外部驱动电阻进行实验，计算获得对应优化中间电平参数为vint=1.5 V、tdint=230 ns.相比5 Ω 外部驱动电阻，优化算法在7.5 Ω 外部驱动电阻下计算的中间电平作用时间推迟且电平值减小.这是由于SiC MOSFET 在7.5 Ω外部驱动电阻下关断速度减慢，因此需向后推迟中间电平作用时间；相应地，由于7.5 Ω 外部驱动电阻下关断损耗增加，关断电压尖峰有所降低，因此需施加相对较小的中间电平值以在有效降低SiC MOSFET 关断电压尖峰的同时，有效抑制关断损耗的增加.

表7 为7.5 Ω 外部驱动电阻下关断损耗对比，图15 为实验测量与模型计算结果对比.由表7 和图15 可知，7.5 Ω 外部驱动电阻下，模型计算结果仍具有较高准确度，漏源极电压尖峰、电压变化率以及关断损耗误差预测均不超过5%.

表7 7.5 Ω 外部驱动电阻下关断损耗对比Tab.7 Comparison of turn-off loss under 7.5 Ω external gate resistancemJ

图15 7.5 Ω 外部驱动电阻下实验与模型结果对比Fig.15 Comparison of experimental and model results under 7.5 Ω external gate resistance

表8 为7.5 Ω 外部驱动电阻下的关断优化特性对比.由表8 可知，相比于CGD，优化AGD 的关断电压过冲降低了30%，而关断损耗仅增加4.2%，对应目标函数为0.87，在增加较小关断损耗的前提下，有效降低了SiC MOSFET 关断电压尖峰，从而减小了EMI.

表8 7.5 Ω 驱动电阻下不同驱动模式的关断特性对比Tab.8 Comparison of turn-off characteristics for different driving modes under 7.5 Ω gate resistance

实验结果验证了所提优化方法对驱动电阻的适用性，所提优化方法可实现不同驱动电阻下优化中间电平参数的计算，以保证SiC MOSFET 工作在关断电压尖峰和关断损耗的优化折衷点.

4 结论

1）针对SiC MOSFET 有源驱动电路中间电平优化参数设计问题，提出一种基于关断轨迹模型的关断轨迹优化方法.通过分析关断过程机理并结合等效电流斜率思路，建立SiC MOSFET 关断轨迹模型，利用基于目标函数的关断轨迹优化方法以优化权衡关断电压尖峰与关断损耗，最后在不同驱动电阻下进行实验，SiC MOSFET 关断特性得到改善.

2）经实验验证，所建关断轨迹模型具有较高的准确性，最大误差不超过10%.所提关断轨迹方法明显改善了SiC MOSFET 关断特性：相比传统驱动CGD，优化AGD 能在不同驱动电阻下降低SiC MOSFET 关断电压尖峰并抑制关断损耗的增加，验证了所提优化方法的有效性以及在不同驱动电阻下的适用性.