整体性思考 结构化学习

从2020年开始，为了实现素养导向、能力立意的“教—学—评”一致性课堂教学改革，引导一线教学从碎片化走向整体化，加强知识关联与衔接，让学生在深度学习中提高课堂教学质量，我们太原市开启了大单元整体备课的本土化实践。课改多年，在我们的思维中，对教学方式的选择过度重视，而对教学内容的理解关注不够。有些老师甚至认为只要课堂放得够开，对学生的主体地位足够尊重，无论讲什么，都是一堂好课。当老师对“教什么”理解不深的时候，“怎么教”就会受到很大制约。我相信，以知识与技能为载体到底要教什么的立意越深远，学生的获益就越大。2022年版课标颁布后，核心素养作为数学课程的统领性目标，明确强化了育人导向，要想让学生整体性思考、结构化学习，教师就先要成为这样的人。下面以苏教版教材三年级上册“两、三位数乘一位数”拓展课为例展开具体说明。

一、课前思考

1.相关的教学事实。

郑毓信教授在《如何很好地发挥数学教育的文化价值》一文中讲述了我国台湾地区一位小学教师的真实困惑——“女儿为什么变笨了”。大致情况是：这位教师带着儿女去吃每人199元的比萨，然后问他们一共要付多少元。小学三年级的儿子口算有困难，向妈妈要纸和笔记录“进位”的过程，幼稚园大班的女儿却借助数数很快得出了结果——“199接着就是200，三个人一共要给600元，柜台阿姨应该再找3元给我们”；可是两年后，三人去吃每人380元的“沙拉吧”，再次计算总价时，两人同时提出需要纸和笔的要求，女儿明确表示没有纸和笔就算不出来。

在一线听课和调研的过程中，我发现类似的情况在我们学生身上也司空见惯，尤其是在学习了笔算乘法并进行大量训练之后就更为明显。有一年太原市提供的四年级期末测评中有这样一道题：实验小学用水缸收集雨水，用来浇花、浇树和打扫卫生。一场大雨后，学校共收集到雨水5000多升。大扫除时，平均每个教室用水102升，这些雨水够36个教室使用吗？解决这个问题，借助口算、估算就可以，102×36=100×36+2×36，或者102×36=102×6+102×30，无论怎么算，得数都只有3000多，连4000都不到，学校收集的雨水绝对够用。可是，自主选用这套试卷的学生一律精确计算，无一人简算。

针对这样的事实，每一位数学老师都应该认真思考这样一个问题：“我们究竟是怎样把学生教笨的？如何改善这种状况？”

2.课标要求。

要想上好计算课，首先要理解“数与运算”主题。2022年版课标以“计数单位”为核心概念，将“数的认识”与“数的运算”贯通起来，就是要表达数的认识与数的运算的一致性。在整数笔算乘法系列课中，“数位”“位值”“十进制”与“计数单位”同等重要。其次要理解运算能力这个核心词的内涵。义务教育阶段的运算能力主要涉及三个问题：一是“如何算”，即对算法与运算程序的运用，表现为运算的熟练性；二是“为什么这样算”，即对算理的理解，表现为运算的合理性；三是“怎样算得更好”，即对算法的优化，表现为运算的灵活性。2011年版课标要求“寻求合理简洁的运算途径解决问题”，2022年版课标要求“选择合理简洁的运算策略解决问题”，两个版本课标的描述异中有同，都要求学生在根据法则和运算律进行正确运算的基础上，对运算策略（途径）是否合理简洁作出判断、比较和选择。

3.内容编排与学情分析。

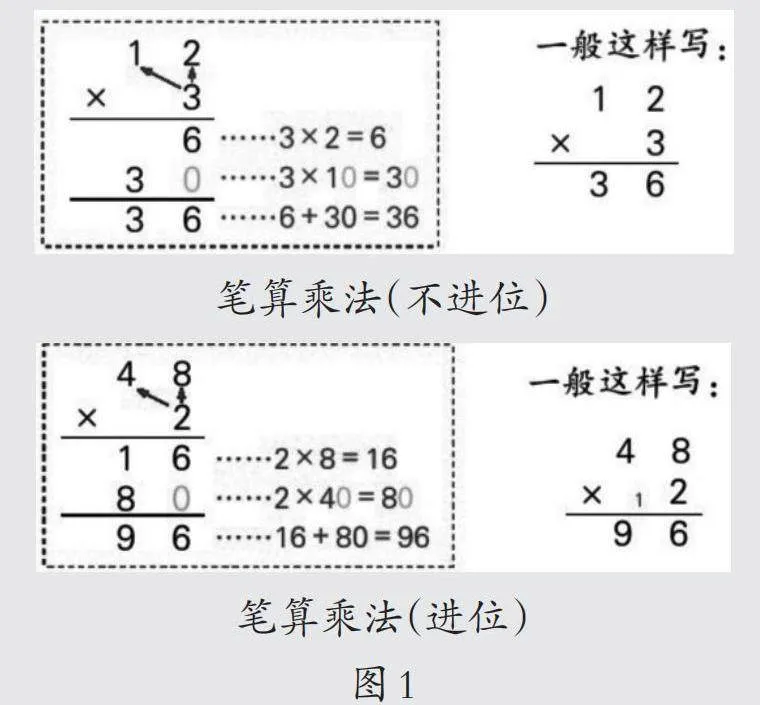
苏教版教材对整数乘法笔算安排了三个阶段：三年级上册“两、三位数乘一位数”，三年级下册“两位数乘两位数”，四年级下册“三位数乘两位数”，之后就是小数乘法、分数乘法了。显然“两、三位数乘一位数”属于笔算乘法系列的起始课。对算理的阐释，课本多次以两位数乘一位数为例，基于位值原理，结合小棒图呈现长竖式到短竖式的简化过程（如图1），并由此迁移到三位数乘一位数以及乘数中间有0、乘数末尾有0的笔算。

在这个内容的教学中，老师们容易将长竖式处理成短竖式成型的辅助，然后瞄准计算的速度和准确率，迅速进入短竖式计算的程序化训练。这样的教学处理和节奏，给学生一种错觉：算理（长竖式）不重要，记住短竖式计算的程序和步骤即可。时间长了，学生的计算思维就僵化了。在学生学习了后续的两位数乘两位数后，铺地锦、印度（日本）算法以及用短视频吸睛的万能法（如图2），让我们的学生屡屡惊叹别人的智慧，只会笔算的无力感催生了他们对习以为常的这种“笨方法”的诸多不解和质疑，却不知这些“无来由的神秘幻术”背后的算理是一致的，就是“位值”，在他们学过的长竖式里就有，稍微调整一下运算的顺序，他们自己也可以创造出来（如图3）。这种事实不只关乎能否选择合理简洁的运算策略，更深刻影响学生学好数学的信心和兴趣。

经过以上对笔算乘法的内容本质、整体知识结构及学生认知规律的分析，从“运算即推理”的理念、笔算乘法的整体发展线索出发，我认为完全可以让长竖式在学生的笔算乘法练习中再保留一些时间，让竖式计算再自由一些，不再拘泥于只能用简化后的短竖式（否则考试就要扣分）计算。在这个单元结束后，上一节三位数乘一位数的拓展课，并以长、短竖式的繁简辩证认识，引发基于简算需求的竖式计算结构的再创造。

二、教学过程

1.梳理结构，回到本源。

教师和学生一起梳理本单元学习的计算内容，有口算、估算、笔算、验算。其中，笔算的内容包括：两、三位数乘一位数（不进位），两、三位数乘一位数（一次进位），两、三位数乘一位数（连续进位），乘数中间有0的乘法，乘数末尾有0的乘法。由此确定本课复习重点是笔算。

学生列竖式计算237×4，并请一名学生描述计算过程，教师板书关键步骤（如图4）。

师：两、三位数乘一位数的笔算，每一步都要回到表内乘法，有进位时，要先心算两步再写一步。

2.长短联系，沟通算理。

（1）借助旧知，异中求同。

教师板书237×4的“长竖式”笔算法（如图5），多数学生表示看不懂。有学生提问：4×7的进位“2”为什么不写在横线上方？竖式里的12是什么意思？

教师继续板书237+237+237+237的计算过程（如图6），边板书边借助手势辅助理解。

学生小组讨论，集体反馈。

生：4×7的进位“2”写在短竖式的横线上方，是因为短竖式里的十位数要算两次才写一步，个位计算得到的进位“2”要先记在脑子里，算完十位的3×4再加上；写在长竖式的横线下方，是因为长竖式本来就是算一步写一步，不用担心忘记。

生：12是4×3得到的。3在十位，表示3个十。4乘3个十得到12个十，也就是120。

生：我来补充，竖式里的8是4×2得到的，4乘2个百得到8个百，8就写在百位上。

教师根据学生回答完善板书，最终结果如图4～6。

师：接下来，我们做一个游戏，我在长竖式里指一步，你也在短竖式里找到和我指的这步一模一样的计算。

教师依次指4×7=28，4×3=12，4×2=8，8+0=8，2+2=4，8+1=9，学生步步对应。

同桌两人再次玩这个游戏。

师：经过刚才的游戏，我们知道三位数乘一位数也可以用长竖式计算。比较一下，如果下次笔算三位数乘一位数，你选择长竖式还是短竖式？

生：我选择短竖式，因为简便。

生：我喜欢长竖式。因为短竖式里有进位时，脑子里算两步才写一步，我经常犯的错误是算了下一步，就忘加上一步的进位了。

师：长竖式虽然写得多，但脑子里记得少；短竖式写得少，但需要脑瓜子灵活，遇到进位，就得口算两步再写一步。这真是繁里有简简亦繁呀！

【思考】华应龙老师说：复习课的成败在“新”“旧”二字。由于课本中没有出现过三位数乘一位数的长竖式，因此，此处教师板书三位数乘一位数笔算的长竖式，会有很多学生看不明白。一来是长竖式笔算法打破了短竖式笔算的惯性思维，二来是不明白长竖式中的步骤和程序。此刻，让学生提出问题，并以加法竖式为支架，能很好地帮助学生基于旧知再发现，进一步理解“位值”的概念。

（2）及时巩固，迁移运用。

师：请一位同学用短竖式笔算207×4，并描述计算过程。

学生边写边说：4×7=28，进2写8，0×4=0，0+2=2，十位上写2，4×2=8，百位写8。

师：其实，计算207×4时，0×4这一步可以省略，只算两步就可以，4×7=28，4×2=8。

部分学生表示自己平时就是这么算的，没有错过。

教师请学生用长竖式的方法笔算207×4，体会这样计算的道理。

生：0乘任何数都得0。乘数的十位上如果是0，当个位计算不进位时，乘积的十位上也是0；当个位计算进位时，进几就在乘积的十位上写几，因为任何数加0都得原数，加的过程可以省略。

教师组织学生用长、短竖式计算230×4，体会末尾有0的乘法的简便算法。

3.算理迁移，迎接挑战。

师：仔细观察237×4，207×4，230×4的长、短竖式，有没有同学能想到，其实237×4还能列出不一样的竖式，计算起来还特别简便？

学生小组讨论，集体反馈。

学生板书新竖式（如图7），班里的同学一片赞叹之声，掌声雷动。我让他们把自己的名字写到竖式旁边，他们很开心，很骄傲。

两个学生为同学讲解，学生的求知欲很强，互动解惑，气氛热烈……

4.回顾反思，总结全课。

师：同学们有没有发现，其实他们这样简算的道理很简单，就是竖式计算的原理——位值。掌握了这个原理，大家的竖式计算就会很自由，根据自己解决问题的需要，可以自由安排计算的顺序，自由选择长、短竖式，将来学习两位数乘两位数等笔算乘法时，希望还能看到你们自己的创造。

【思考】事实上，237×4还有其他笔算方法，例如从高位算起。只要理解算理，把握核心概念，程序性知识也可以灵活变换。以不变应万变的前提是我们发现了其中的规律。在这个片段中，我以学生已经理解和创造的237×4、207×4等长、短竖式为支架，让学生再创造笔算237×4的简便算法，有挑战、空间大。跳一跳就能摘到果子的经历，不仅让学生触及若干知识的核心概念，把书读薄，也让学生看到了更好的自己，甚至体会到了数学的逻辑美、结构美。用数学学科本身的魅力吸引学生，欣赏数学美，这不就是素养导向、能力立意的教学追求吗？

三、启示与思考

1.2022年版课标颁布，标志着我国基础教育课程改革又跨入了一个新的历史时代。核心素养具有整体性、一致性和阶段性，对应课程内容结构优化，要求全学年、全学段、全学校的数学老师，无论是新入职，还是常年只教某个年级或学段，都必须整体分析主题、单元和课时内容结构，清楚地知道自己所教知识的前后联系，充分发挥核心素养导向的教学目标对教学过程的指导作用，帮助学生建立能体现数学本质、对未来学习有支撑意义的结构化知识体系，学会用整体、联系、发展的眼光看问题，形成科学的思维习惯。

2.教师立足知识结构整体思考的思维方式，带来的最大好处是能直面那些年年教年年有、年年解决不了的顽固问题，重新定位单元整体教学视域下的课时内容，找到解决策略，以种子课、生长课、思维拓展课等多种形式提升教学效果。例如这节三位数乘一位数的拓展课，就立足解决运算思维僵化的问题，通过整体分析笔算乘法的知识线索，找到以“位值”为核心概念的具体解决路径，支撑学生整体建构笔算乘法的算理理解，提升了运算能力。

3.教育理应培养适应未来社会的人才，但未来世界什么样，我们完全无法想象。最近很火的chatGPT，已经可以“拟人化”思考，高质量完成写作、写程序、画画等我们以往认为人类最有创造力、机器无法替代的事情。人工智能的高速发展对教育的影响可能是颠覆性的，由此也再次引发我们对“培养什么人、怎样培养人”的思考与叩问，作为基础教育的数学教师，我们目前能做的，就是回归教育初心，回到“原理”理解，注重培养创造性思维，为学生未来能够驾驭人工智能奠基。

【本文系山西省教育科学“十四五”规划课题“核心素养视域下中小学学科思维培育策略的研究与实践”（编号：GH-220293）、太原市教育科学“十四五”一般规划课题“小学数学‘教、学、评一体化’的大单元整体设计的实践研究”（编号：GH-22034）的阶段性成果】

（作者单位：山西太原市教研科研中心）