怎么做可以更好地理解“浸没”问题

“浸没”问题是学习圆柱与圆锥体积后的延伸问题，怎样做可以帮助学生更好地理解？可以采用以下教学环节。

一、从简单入手，根据立体图形截面大小判断折线变化情况

1.提出问题，描述截面。

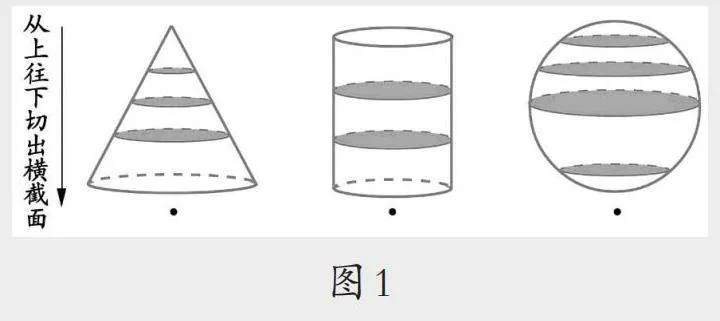
出示图1，提问：每个立体图形的横截面是什么形状？学生独立思考后与同桌交流。预设学生发现三个立体图形的横截面都是圆形。

2.比较大小，描述变化。

提出思考：从上往下依次切出横截面，横截面的大小是如何变化的？学生在组内进行交流。预设：从上往下切，圆锥的横截面逐渐变大；圆柱的横截面相同；球的横截面先变大再变小。

3.读懂图意，直观表达。

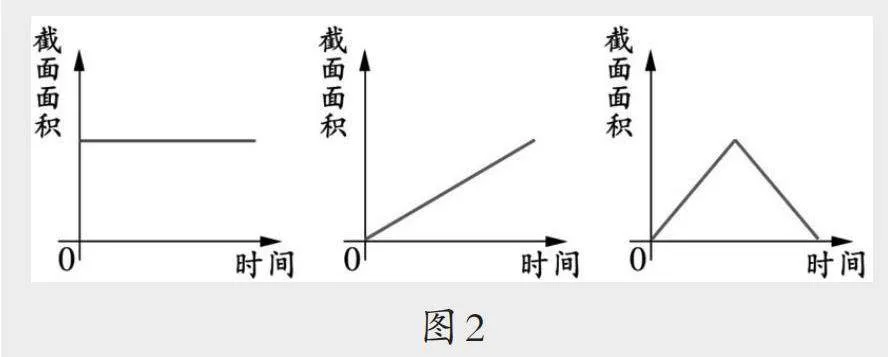
出示图2，提出思考：你能看懂这三幅折线图吗？请学生介绍横轴和纵轴表示的意思。横轴表示从上往下切的时间，纵轴表示横截面的大小变化。请学生将折线图与对应的立体图形用线连一连，并说一说想法。

二、提高难度，根据容器形状推测水位变化情况

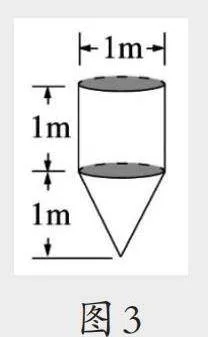
出示图3，提问：一个圆柱与一个圆锥合在一起做成的水箱，以相同的水流速度往空的水箱中注水，注水时间和水面高度会如何变化？请学生尝试在空白图上画一画（如图4），然后反馈学生作品。

三、反向逆推，根据折线变化情况推测容器的形状

1.读懂图意，尝试画图。

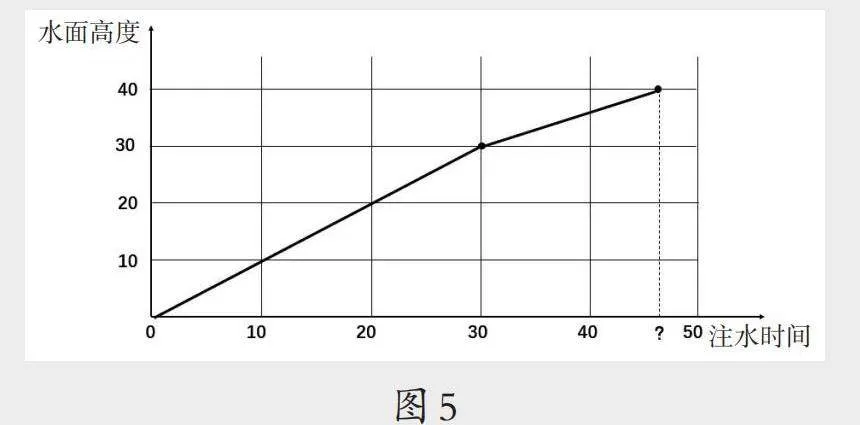
出示图5，提出问题：往容器里注水，注水速度不变，根据折线变化情况猜测容器的形状。学生尝试画容器图，组内交流想法，教师巡视，选择典型的作品进行展示。

2.呈现作品，表达想法。

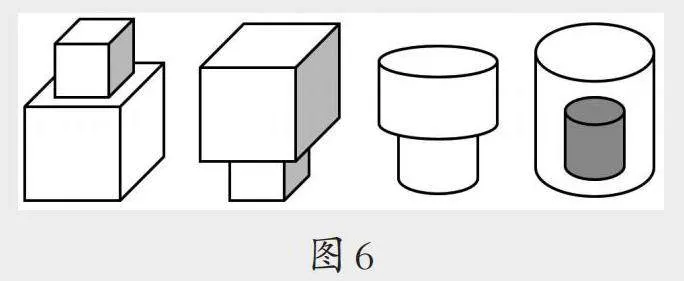
呈现学生的作品，预设学生可能的答案（如图6），让其他同学进行判断，表达自己的想法。

运用数形结合方法，解决较复杂的“浸没”问题，有助于促进学生空间观念和推理意识的培养，提高解决问题的能力。

（作者单位：浙江杭州市上城区崇文实验学校）