“角的度量（一）”教学实录与评析

【课前思考】

学生在二年级上学期初步认识了角，知道了角的组成，也已经初步感知角的大小跟角的两边叉开的大小有关，跟角的两边（画出的部分）的长短无关。“角的度量（一）”是北师大版教材四年级上册第二单元的内容。在这节课中，学生主要经历角的度量的操作过程，认识角的度量单位，即1°的角。教材创设了滑滑梯的情境。针对这个情境，可以从以下三个方面开展教学：第一个方面，思考用哪些方法可以度量角的大小；第二个方面，经历用小角量大角的操作过程；第三个方面，了解1°的角有多大。学生通过本节课的学习，认识到“量角器的本质是单位小角的集合，角的度量的本质是看被测对象中含有多少个‘单位小角’”。

【教学过程】

一、情境引入，激发兴趣

师：同学们，玩过滑滑梯吗？请想象一下分别从这两个滑梯（图略）上滑下来会有什么感觉。

生：1号滑梯很矮，从上面滑下来会感觉很舒服。

生：2号滑梯太高了，玩起来应该特别刺激。

师：这两个滑梯能带给我们不同的感觉，其实与一个数学知识有关，你们知道是什么吗？

生：角。

师：对，就是与滑梯面和地面形成的夹角有关。怎样测量角的大小呢？这节课我们一起研究这个问题。

教师板书课题。

评析：从学生生活经验出发，激发其学习兴趣，沟通生活与数学之间的联系，培养学生用数学的眼光观察生活的良好习惯，引发他们的数学思考，唤醒学生对角进行度量的需求，使学生明确本节课的学习内容。

二、复习旧知，探究新知

1.复习旧知。

教师把滑梯面和地面形成的夹角画到黑板上，让学生回忆角的组成、记法、读法。

评析：学生复习角的有关知识，培养符号意识，从中体会数学的简洁美。

2.比较角的大小。

（1）观察法。

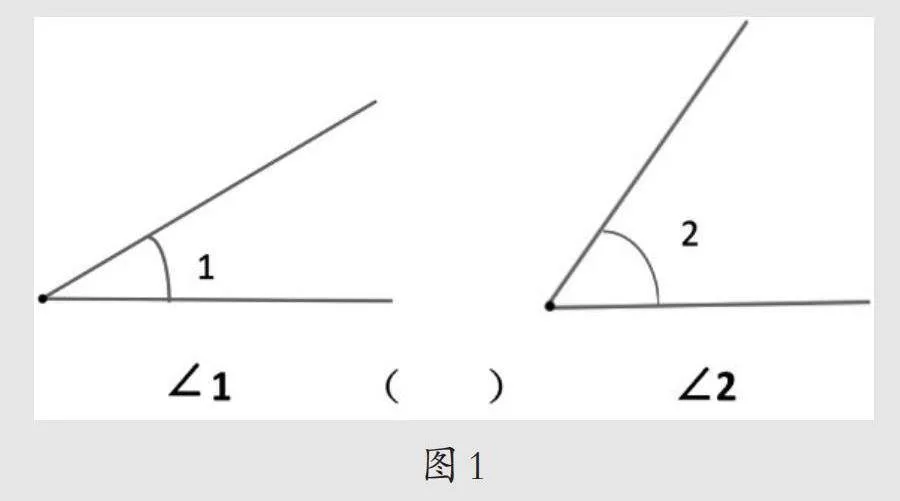
教师呈现图1，引导学生得出：当两个角的大小相差很大时，可以直接通过观察比较。教师指明这叫作观察法。

（2）重叠法。

教师呈现图2，引导学生得出：当两个角的大小比较接近时，用观察法很难做出准确的判断，这时可以将两个角的顶点重合，其中一条边重合，观察另一条边。教师指明这叫作重叠法。

（3）标准角法。

师：你还能想到其他方法比较∠1和∠3的大小吗？

师生一起回顾线段的度量和面积的测量：用1cm长的短线段作为标准可以测量较长线段的长度，用面积为1cm2的小正方形作为标准可以测量较大的图形的面积。

师：现在，要测量∠1和∠3的大小，你从上面得到了什么启发？

生：可以用小一点儿的角测量大一点儿的角。

师：你真是善于思考的孩子，小角量大角也是一种度量的方法。

教师板书：小角量大角。

师：老师给你们每个组都准备了一个锦囊，这些小角就藏在这个锦囊里面。“实践是检验真理的唯一标准。”接下来，请同学们利用锦囊里面的工具做个实验，比较∠1和∠3的大小。

学生操作。

师：通过刚才的研究，你们得到了怎样的结果？

组1：我们用红色的小角去比较，发现∠1里面刚好可以放下3个小角，∠3里面可以放下4个小角，从而得出∠1比∠3小。

师：他们用红色的小角作为标准，量出∠1正好包含3个红色标准角，把它记作3，可以吗？

生：可以。

师：∠3正好包含4个红色标准角，记作几？

生：4。

师：3比4小，所以∠1比∠3小，同意吗？

生：同意。

组2：我们小组用蓝色标准角去比较，发现∠1里面刚好可以放下2个蓝色标准角，∠3里面放2个蓝色标准角有剩余，但放不下3个蓝色标准角，从而得出∠1比∠3小。

师：∠1正好包含2个蓝色标准角，可以记作几？

生：2。

师：∠3怎么记录呢？

生：2点几。

师：到底是2点几？反正比2大比3小，就记作2.□，可以吗？

生：可以。

师：2比2.□小，所以∠1比∠3小。

评析：直观观察是学生学习的重要方法和基本能力；重叠法的学习旨在引导学生认识角的大小比较方法的多样性，渗透了度量角的方法“两合一看”；根据线段的度量、面积的度量、角的度量的纵向联系，通过知识的迁移，引导学生联想到小角（标准角）量大角的方法，悟出用小角（标准角）测量的可行性和操作要点，在操作中再次感悟量角的方法，深刻理解“一个角的大小，可以从它所包含的标准角的个数来判断”这一度量的本质，为以后学习体积的度量奠定基础。

3.认识角的度量单位。

（1）感悟度量标准的统一，引出度量单位。

师：∠1一会儿用3表示，一会儿用2表示，难道∠1的大小还会变？

生：不会。

师：那为什么一会儿用3表示，一会儿用2表示？

生：因为标准角的大小不一样。

师：是的，标准不一样，得到的结果就不一样。为了统一，我们需要约定一个度量的标准，你们知道是什么吗？

（2）渗透数学文化，建立1°的角的表象。

师：其实，数学上，通常用1°的角作为度量角的大小的标准。

教师板书：1°。

课件展示：1°的故事。（略）

师：把一个圆平均分成360份，每份所对应的角的大小就是1度，1度在数学上可以记作1°，通常用1°作为度量角的单位。

教师带领学生比画1°的角有多大。

评析：通过用不同标准角度量同一个角会产生不同的结果，引发矛盾，让学生在冲突中理解统一标准的意义，从而自然引出对角的度量单位的认识，此时嵌入“1°的故事”这一数学文化内容，激发学生的学习热情，使其建立1°的角的表象。

4.感悟度量本质，培养量感。

学生在圆上认识不同的角：5°、10°、50°、45°、110°的角，然后估计红色的小角和蓝色的小角有多大，再放到圆上比较，最后得出：红色的小角包含圆上的1个大格（10°），所以是10°；蓝色的小角包含圆上的1个大格和5个小格（1°），所以是15°。

师：看来要准确判断一个角的度数，只需要把角放到这个圆上，数清楚这个角包含几个大格、几个小格就可以了。

评析：引导学生建立红色的小角与蓝色的小角和圆上的大格与小格之间的联系，促使他们深刻理解“判断一个角的大小，就是看这个角包含的1°或10°的角的多少”，从而培养他们的量感。

三、拓展延伸，加深理解

师：你能在这个圆上找出一个80°的角吗？找一找、画一画。

学生找和画。

师：你画的角是80°的角吗？怎么确定？

生1展示并分享：这个角里面有8个大格，每个大格是10°，8个10°就是80°。

生2展示并分享：我画的这个角也是80°，而且给它标上了数据，有8个10°就是80°，这样更清楚。

师：看到生2的方法，你们有何感想？

生：标上数据后，观察起来方便多了。

师：是的，数据能给我们一目了然的感觉。

生3展示并分享：我有更好的方法，从0开始标上数据，依次是10、20、30、…、80，这样不用数，直接就可以看出来是80°。

师：听了他的方法，你们又有何感想呢？

生：这样从0开始，依次标下去，不用数就可以得出结果，更加方便。

师：一直标到180，看看你有什么发现。

生：0和180在一条直线上。

生：我发现了一个半圆。

师：现在我们把这个圆沿着0和180所在的直线对折，你有什么新的发现？有没有熟悉的感觉？

生：像一个量角器。

师：恭喜你们亲手创造了一个量角器，真了不起！你们知道量角器是用来干什么的吗？

生：量角的。

师：是的，量角器就是一种用来测量角的大小的工具，下节课我们将详细认识量角器，并学习怎样使用量角器测量角的大小。

评析：学生经历自创简易量角器的过程，产生巨大的成就感和自豪感，进一步激发学习兴趣，也为学习用量角器量角奠定基础。

四、回顾反思，全课总结 （略）

（作者单位：四川眉山市仁寿师范附属小学）