在协商中梳理 在思辨中理解

2022年版课标在数与运算主题中，明确提出要让学生达到“感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识” 的学习要求。“小数乘法”单元学习内容包括小数乘法笔算、小数简便运算及解决问题三部分内容，从复习课让学生体会运算一致性的教学目标思考，应让学生在复习梳理时理解小数乘法与整数乘法在笔算、简便计算与解决问题时的一致性。即小数乘法的算理、算法与整数乘法相同，小数简便计算与整数乘法原理相同，用小数解决问题与用整数解决问题方法也相同。针对这一复习目标，应设计整体性的复习材料，让学生在比较、思辨中理解一致性。基于这样的认识，我们进行了实践探索，取得了很好的效果。

一、在思辨交流中梳理算理算法的一致性

1.协商对话，梳理算法。

课件出示下列8个算式（如图1）：

师：今天进行小数乘法的梳理与复习。计算这8个算式前，你会有什么想法？

生：今天复习的是小数乘法，但这8道题有小数乘法，也有整数乘法，我想可能会涉及小数乘法与整数乘法的联系吧。

生：我发现这8道题的数据一样，只需要用竖式计算1道题就能直接写出其他题目的积。

师：是这样吗？那你们会选择哪道进行笔算？为什么？

生：我会选择第④题“4.5×6.2”这个算式，因为今天复习小数乘小数。

生：我会选择“45×62”这个算式，因为这个算式计算最方便。

生：我也会选择第③题“45×62”这个算式，但要补充一些原因。因为小数乘法都是先按整数乘法计算，再根据因数的小数位数从积的右边起点小数点。

师：你们能选择具体例子算一算，再介绍他的思考方法吗？请先想一想、算一算，然后在小组内说一说。

评析：教师通过富有联系的8个算式，将小数乘法与整十、整百数乘法放到整数和小数乘法的大整体中，以开放的数学问题，激发学生思考的兴趣，进一步理解小数乘法与整数乘法算法的密切联系。再依据学生汇报、师生对话，自然而然地复习梳理小数乘法的算法与整十、整百数乘法的算法。

2.沟通联系，思辨算法一致性。

学生独立计算，小组交流后汇报。

生1：我以45×6.2为例，先末尾对齐，按45×62算出积是2790，因为因数6.2是一位小数，就在积上从右往左数一位点上小数，再去掉小数点末尾的0，得到了279。

生：我计算的是4.5×0.62，也是先按45×62算出积，是2790，因为4.5看作45，扩大为原来的10倍；0.62看成62，扩大为原来的100倍。积扩大为原来的1000倍，原来的积要乘0.001，就是将小数点向左移动3位，得到积为2.79。

生：我计算的是450×620，因为450里有45个10，620里有62个10，也是先算出45乘62的积，再乘100。

……

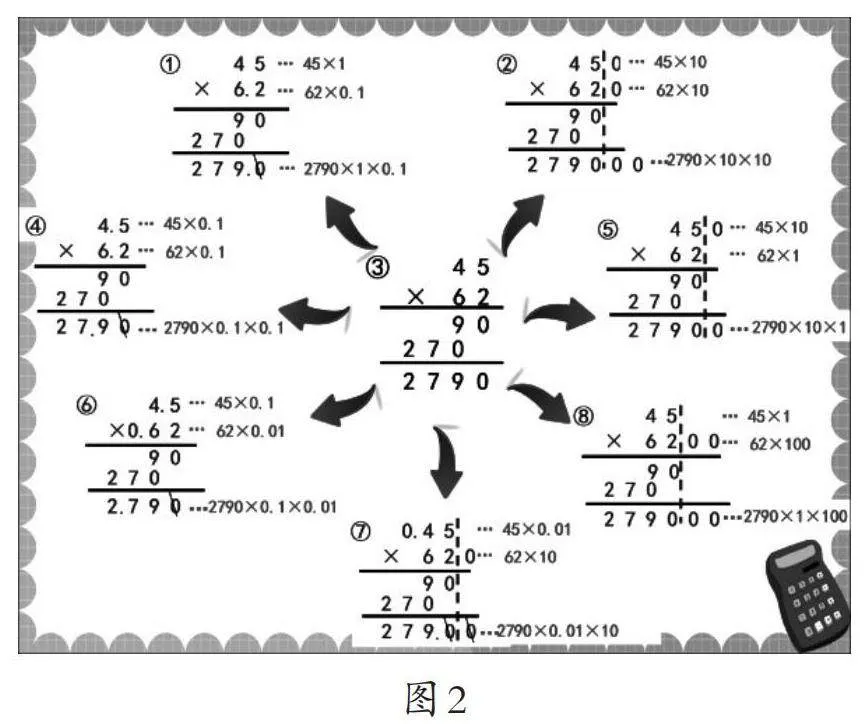
根据学生的汇报，通过对话，课件呈现如下内容（如图2）：

师：通过对这些算式计算过程的观察，你能明白什么？

生：我明白了小数乘法先按整数乘法的方法计算出积，再根据因数的小数位数点上小数点。

生：我发现整十、整百数乘法与小数乘法的方法是一样的，按末尾没有0的整数乘法算出积，因数中有几个0，就在积后面添几个0。

生：不管是小数乘法还是整十、整百数乘法，方法都是一样的，按整数乘法计算出积后，根据因数中的意义，再用积乘100、10、0.1、0.01等。

师：这里的100、10、0.1、0.01是整数、小数的计数单位，你的意思是用积再乘计数单位，是吗？

学生肯定答复：并且都是积乘两个因数的计数单位。

师总结：整十、整百数及小数乘法先按整数乘法计算出积，再分别乘因数的计数单位。

评析：小数乘法笔算先末尾对齐，按整数乘法计算后依据因数的小数位数点上小数点，该方法只是小数乘法的表面现象，并未触及小数乘法算法的本质，即数与数的积乘计数单位与计数单位的积。而本环节呈现整十、整百数乘法与小数乘法的整体对比材料，借助整十、整百数乘法末尾不对齐这一表象的矛盾，理解末尾对齐不是算法的本质属性，突出了计数单位在运算中的独立性，在不同算式运算方法的沟通中进一步理解算法的一致性。

3.质疑过程，感悟算理一致性。

师：根据你们发现的计算方法，你能结合④⑥⑦这三道题具体解释一下吗？

生：4.5×6.2的计算方法是45×62×0.1×0.1，其中45×0.1是4.5，62×0.1是6.2。

生：4.5×0.62的计算方法是将因数4.5看作45×0.1，因数0.62看作62×0.01，按45×62×0.1×0.01来计算。

生：计算0.45×620，因数0.45等于45×0.01，因数620等于62×10，所以0.45×620=45×62×0.01×10。

根据学生的回答，教师随手在黑板上写出如下横式：

④4.5×6.2=（45×0.1）×（62×0.1）=45×62×0.1×0.1

⑥4.5×0.62=（45×0.1）×（62×0.01）=45×62×0.1×0.01

⑦0.45×620=（45×0.01）×（62×10）=45×62×0.01×10

引导学生观察后，师提出：“先按整数计算出积再乘计数单位的积”的依据是什么？

学生交流后得出：依据数的意义，再运用乘法交换律与乘法结合律。

师总结：刚才我们通过对三道题计算方法的梳理，不但知道了小数乘法怎么算，还知道了这样算的道理。

评析：知其然，更要知其所以然。在本环节教学中引导学生质疑，结合具体算式的分析，在观察比较中发现运算定律是乘法算理的依据。

二、在目标协商中感悟简便运算的一致性

1.过渡，引发思考。

师：通过刚才的复习，我们知道小数乘法计算过程中，除运用乘法交换律与结合律外，还运用了什么运算定律？请结合“4.5×6.2”说一说。

生：还运用了乘法分配律，因为计算“4.5×6.2”时，可以把6.2看作（6+0.2），先用0.2乘4.5，再用6乘4.5。就是4.5×6.2=4.5×（6+0.2）=4.5×6+4.5×0.2。

师：看来小数乘法笔算并不简单，中间包含了乘法交换律、结合律与分配律的综合运用。

2.开放编题，梳理方法。

师：运用乘法运算定律可以使一些小数运算更加简便，程老师心中就有可以简便运算的一个综合式子，这个式子的前面一部分是“8.8×2.5”，你能猜测出这个式子吗？请写出这个式子，进行简便运算，并说说你是如何思考的。

学生猜测、运算、交流后，呈现作品并交流。

生1：我猜算式是“8.8×2.5+2.5×1.2”，因为8.8加1.2等于10，10乘2.5等于25。

师：你是将2.5作为公因数，根据与8.8这个数可凑成整十想到1.2，再写出的式子，并依据乘法分配律简便计算。

师：依据这个式子，你能联想到原来哪个整数简便运算的式子？

生1：我联想到88×25+25×12这个整数运算式子，它们的计算方法是一样的。

生2：我写的算式是8.8×2.5÷2.2，依据交换律得到8.8÷2.2×2.5，算出积是10。

师：补充“除以2.2”，你是依据什么思考的呢？

生2：依据2.5这个数思考的，因为2.5乘4是10，刚好凑整，而8.8除以2.2会得到4。

生3：看到2.5我马上想到了4，我就直接在后面乘4，算式是8.8×2.5×4，再依据结合律进行简便计算。

生4：我把8.8作为公因数，2.5减去1.5等于1，算式是8.8×2.5－8.8×1.5，依据乘法分配律进行简便计算。

生5：我想的算式就是8.8×2.5，它本身就可以简便计算，因为8乘25是200，把8.8看成（8+0.8），再依据乘法分配律就可以简便计算了。

师引导学生进行比较：小数乘法中的简便运算与四年级学习的整数乘法简便运算有什么共同点？

生1：小数乘法的简便运算与整数乘法的简便运算是一样的。

生2：都运用交换律、结合律或者分配律进行简便计算。

生3：都是运用运算定律进行凑整。

评析：以简便运算为目标开展编算式、简便运算，这种思维在前、导向驱动的方式能唤起学生对简便运算的已有经验，突出运用运算定律凑整这一简便运算的基本策略。虽然没有直接呈现整数简便运算，但学生通过回忆能简便运算的整数算式并联系两者的共同点，能感悟到简便运算的一致性。

三、在比较联系中思考解决问题的一致性

1.出示，引应用。

（1）一个长方形房间长8.8米、宽2.5米，这个房间占地面积是多少？

（2）一个长方形房间长8.8米、宽2.5米。现在要铺上边长为0.8米的正方形地砖，50块够吗？（不考虑损耗）

（3）装修师傅贴地砖收费标准如下：2.5平方米以内，每平方米收费8.8元；超过2.5平方米（不足1平方米的按1平方米计算）的部分，每平方米收费7元。小亮家贴地砖面积为60平方米，要付多少钱？

2.交流，聊方法。

学生独立解决、小组交流后汇报。

生：第（1）题因为长方形的面积是长乘宽，所以算式是8.8×2.5=22（平方米）。

生：第（2）题我是这样想的，因为边长是0.8米的正方形，面积是0.64平方米，50块的面积就是0.64×50=32（平方米），而前面我们已经算出房间的面积是22平方米，所以是够的。

生：如果前面不知道房间的面积是22平方米，解决第（2）题时可以用估算的方法来想，因为50块地砖的面积是0.8×0.8×50，用结合律简便计算，积是32平方米，把8.8看作9，2.5看作3，房间的面积往大估是9×3=27（平方米），还不到32平方米，所以是够的。

师：估算在有些时候是一种好办法，如果这个房间的长是8.8米、宽是4.1米，怎么估算？

生：可以往小估，把8.8估成8，4.1估成4，8×4=32（平方米），估小了刚好，说明不够。

生：第（3）题是阶段计费，因为2.5平方米以内，每平方米收费8.8元，所以要8.8×2.5=22（元），一共60平方米减去2.5平方米等于57.5平方米，这部分每平方米收7元，需要58×7=406（元），406元加上22元等于428元。

师：运用分段计费解决问题时应注意什么？

生：要注意是每平方米收费还是一共收费。

生：不足1平方米的要按1平方米计费。

生：要注意有时候是超过部分按每平方米收费，而有时候是超过后按每平方米收费。

师：你能举个例子吗？

生：这道题是超过部分每平方米收7元。有时是这样的：超过2.5平方米，每平方米收费7元，说明全部60平方米都是收7元的。

师：同样道理，小数与整数在解决问题中也存在联系。想象一下，如果将这三道题中的小数全部换成整数，你会发现什么？

生：我发现思考的过程是一样的。

生：数据全部是整数时就不用估算了，可以直接计算。

生：我不同意，如果接近整十的，也有可能把整数估成整十数呢。

师总结：整数与小数解决问题时的思考方法相同。

评析：在本环节教学中，以房间铺地砖这一主题开展复习，有利于学生在自主解决问题、小组交流的过程中感受到小数在生活中的重要作用。同时，在练习过程中通过师生对话，理解小数与整数解决问题思考方法是一致的道理，有利于学生在解决问题时回归题目的本质思考，提高用小数解决问题的信心。

（作者单位：浙江临海市哲商小学）