基于课程标准的小学数学命题设计

评价是课堂教学的指挥棒，只有命题依托于新课标，老师的教和学生的学才能更精准地落实新课标要求，因此命题的设计质量决定了教学的质量。下面，笔者结合新课标的要求，给出基于新课标的小学数学命题的策略，期望能起到抛砖引玉的效果。

一、借助尺规作图，发展几何直观

在小学数学命题设计中，可以增加对学生尺规作图能力的考查，学生经历观察、分析、思考、操作等过程，可以提高分析问题和解决问题的能力，并让思维从操作实验的具象直观，逐步向推理论证的严谨抽象过渡，助力学生的几何直观和空间观念的有效形成。

样题1：要给长方形的图画做一个相框进行装饰（如图1）。现有装饰用的一段木条如线段MN所示。不用刻度尺测量，你能用尺规作图的方式判断这段木条够不够吗？（保留作图痕迹，不考虑各段木条接头处的损失）

样题1是一个生活情境的题目，考查的知识点是周长的认识，要求学生能用直尺和圆规将长方形的四条边画到一条直线上，可以利用线段长度的可加性直观地判断木条材料够不够。该样题需要学生将图画的相框抽象成长方形的周长，并通过尺规作图的方式直观地比较长方形的周长和材料的长短关系。

二、整合结构化知识，深化数学本质

在小学阶段“数与运算”主题中，在理解整数、小数、分数意义的同时，还要理解整数、小数、分数基于计数单位表达的一致性。在平日的教学中，重视教学内容的整体分析和一致性教学，可以帮助学生在头脑中形成系统的知识框架，建立体现数学学科本质的数学知识体系，实现有效的学习。

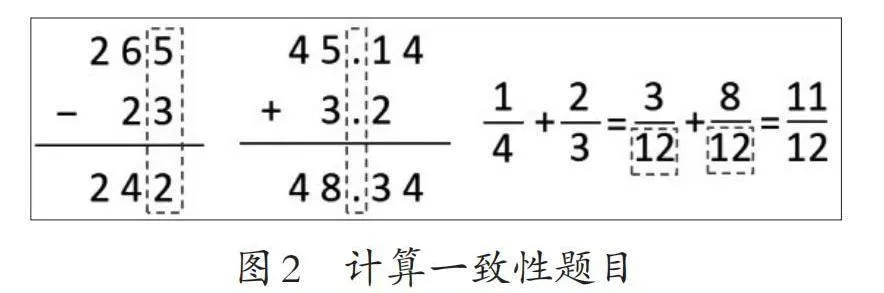
样题2：在小学阶段，我们分别学习了整数、小数、分数的加减法（如图2）。在计算时，整数的加减法要“末位对齐”，小数的加减法要“小数点对齐”，分数的加减法要“先通分再计算”。它们的计算方法看似不同，但在计算原理上是相同的。

（1）“265-23”中是5个（ ）减3个（ ）等于2个（ ）。

（2）“45.14+3.2”中是1个（ ）加2个（ ）等于3个（ ）。

（3）“[1/4+2/3]”中转换成了3个（ ）加8个（ ）等于11个（ ）。

（4）我发现整数、小数、分数的加减计算都是（ ）。

样题2是一个数学情境的题目，考查的知识点是学生学完异分母分数的加减法后，要求能通过列举的算式，理解整数、小数、分数的加减运算都是相同的计数单位相加减，感悟运算的一致性。

三、创设真实情境，指向核心素养

在教和学的过程中，教师要借助真实情境，引导学生经历发现问题、提出问题、分析问题、解决问题的全过程，实现“四能”的落实。根据“教—学—评”一致性的原则，在进行学业评价时，也要尽量依托真实情境来测评。

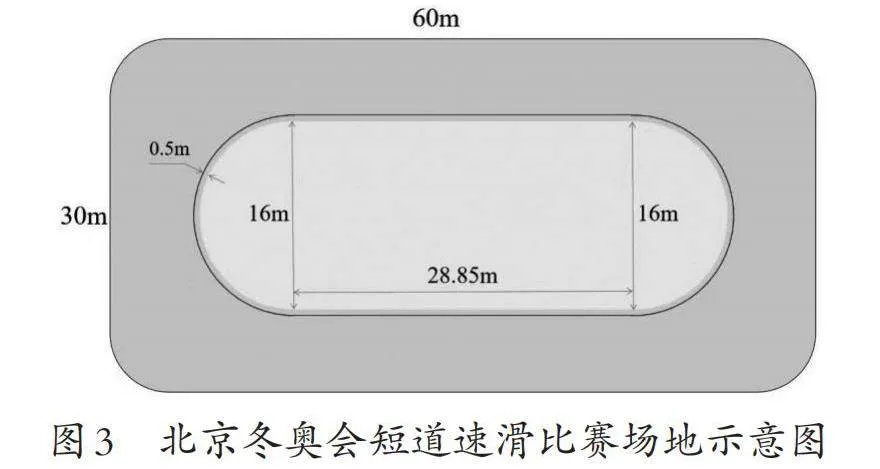
样题3：2022年北京冬奥会短道速滑比赛场地长60米、宽30米，跑道是由两条直道和两个半圆形跑道组成的（如图3）。直道长28.85米，最内圈半圆直径为16米。第一条跑道距离最内侧0.5米，如果在这个跑道上比赛，一圈长度为多少米？（π取3.14）

样题3是一个真实情境的题目，解决的是冬奥会短道速滑跑道长度的实际问题。考查的知识点是圆的周长计算，要求学生能利用圆的周长计算公式，解决跑道周长的问题。学生经过分析，将跑道抽象为“一个圆+两条线段”的周长的数学问题，利用圆的周长的计算模型，解决实际问题。

四、感悟数学文化，渗透育人价值

教材在编写时会加入《九章算术》《几何原本》等书中的数学文化内容。在教学过程中，教师也可以让学生体验相关的数学文化，展现数学发展史中我国著名数学家的数学成果，让学生感受我国数学家的卓越贡献。在试题命制时，也可以适当选取中华优秀的数学文化素材，渗透正确的人生观和价值观，充分体现数学学科的育人价值和功能。

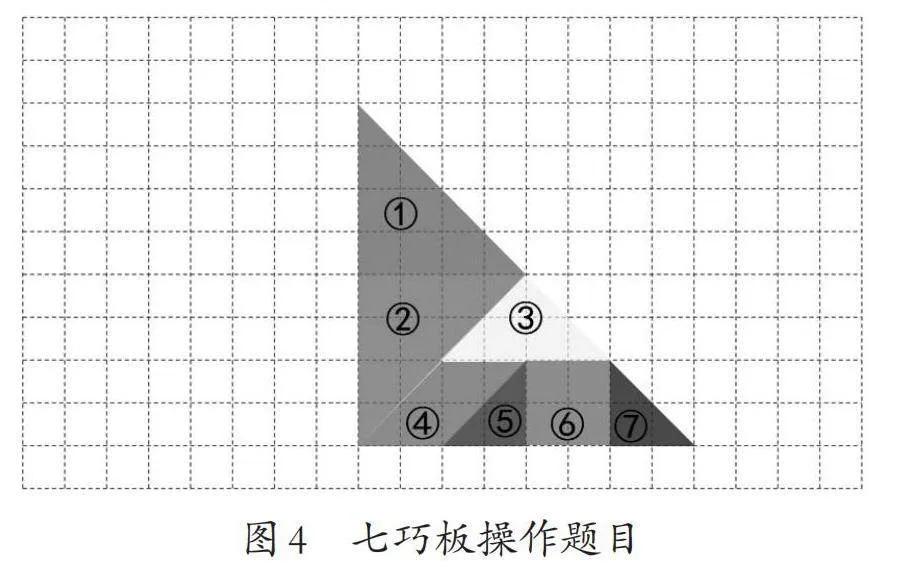
样题4：七巧板是一种古老的中国传统智力玩具，图4是一副七巧板拼成的大三角形。请你只移动其中的一块七巧板，将拼成的三角形变成梯形。请你利用平移和旋转的数学知识，写出平移和旋转的过程。（可以用字母A、B、C等标注移动的七巧板的顶点，并在方格纸上保留移动痕迹）

该题考查的知识点是平移和旋转，要求学生能根据图形特征，分析需要操作哪块七巧板，并在头脑中进行变换与比较，得到所求梯形的表象。

五、探索跨学科设计，培养应用意识

跨学科主题学习活动，可以培养学生在跨学科背景下用数学的眼光观察现实世界，并用数学学科和跨学科的知识与方法，解决真实世界中真实问题的能力，帮助学生感悟数学与现实世界的联系，培养学生的实践精神。

样题5：周期蝉在自然界进化出了非常特别的繁殖周期，目前发现的有13年蝉、17年蝉等，也就是它们的幼虫需要在地底下分别生活13年、17年才能破土而出。为了逃避天敌的侵害并安全延续种群，它们进化出一个漫长而隐秘的质数生命周期（13、17都是质数）。如果周期蝉与它的具有一定繁殖周期的天敌在同一年出现，天敌的幼虫就会以蝉的幼虫为食，对蝉的种群延续是很不利的。

以17年蝉和繁殖周期为5年的天敌为例，假设在第0年时，蝉和天敌第一次相遇，请你根据下面的百数表（如表1）完成下面几个问题：

（1）用“△”标出17年蝉的出土年份。

（2）用“○”标出繁殖周期为5年的天敌的出动年份。

（3）观察表1，17年蝉和天敌在第（ ）年相遇，此年正好是17和5的（ ）。

样题5是一个数学和科学的跨学科题目，周期蝉的形成是大自然物竞天择的结果。周期蝉选择质数的生命周期，可以在很大的机会上避免和天敌的生命周期发生重叠，实现种族的延续。该题考查的知识点是因数、倍数和最小公倍数，首先学生需要用数学的眼光读懂周期蝉的秘密，继而发现蝉的出土年份、天敌的出动年份其实就是它们的生命周期的倍数，而两者相遇的年份就是两者生命周期的最小公倍数。

（作者单位：山东青岛实验学校）