数学实验：架起知识到实践的桥梁

四年级学生学习了角的认识和度量后，知识的应用往往局限于“生活中找角”“测量角的大小”上，但这仅仅是对知识的简单应用和操作，并不是真正意义上的学科实践。所谓学科实践是源于对学科知识与生活现象本质的理解和应用，具有跨学科性和联系性。如何开发一节数学实验课，让学生经历从学科知识到学科实践的“真探究”“真实践”过程呢？“镜子里的秘密”这一数学实验项目，其目的就是在学习“角的度量”后，将数学与科学知识整合，架起知识到实践的桥梁，使学生经历数学建模过程，发展核心素养。该数学实验借助平面镜工具，让学生经历“角度与虚像的函数关系”数学建模过程，实现角度知识的迁移应用。通过观察、猜想、实践、归纳、推理等思维过程，培养学生综合应用知识的能力和实验探究力。这节实验课可以安排在“角的度量”学习后，增设一节拓展性的数学实验课，具体实验探究过程呈现如下。

一、观察单面镜，了解虚像[ ]

1.初识万花筒，引出镜子。

师：今天老师给大家带来了一个玩具（出示万花筒），这个万花筒里面真的藏着千千万万朵花吗？

生：其实没有那么多花，但因为里面有镜子，通过反射，就可以看到无数朵花。

师：看来产生那么多花是因为镜子的缘故，同学们想知道其中的奥秘吗？今天这节课我们就来研究“镜子里的秘密”。

2.通过单面镜，了解虚像。

师：老师给每位同学都准备了一面平面镜，大家照一照，你看到了什么？

生：在镜子里面看到了我自己。

师：镜子里真的还藏着一个你吗？

生：镜子里面是我的虚像，不是真实的我。

师：是的，镜子里面并不是真的有一个人，而是光线通过镜子反射到眼睛里，产生的物体的虚像。

【设计意图】从学生熟悉的万花筒入手引发猜想，激起学生探索万花筒成像数量的奥秘，从而将一个常见的科学现象与数学知识建立联系，既有学科融合又将数学应用于生活，真正发展学生数学素养。

二、调整双面镜，观察变化[ ]

1.任务驱动，建立猜想。

师：你从这面镜子里看到了自己的几个虚像？（生：只有1个）如果想看到更多的虚像，可以怎么做？

生：增加镜子。

师：增加几面呢？

生：2面或者3面。

生：2面就够了。

师：增加镜子就可以让虚像变多吗？

生：还需要转换一下角度。

师：你真会思考！2面镜子怎么转换角度呢？

生：可以连接一端，让2面镜子的夹角变大或变小，镜子的位置发生了变化，角度也就发生了变化。

师：这样的镜子，我们暂且称为双面镜。

2.操作实践，观察验证。

师：夹角变化真的可以使虚像变多吗？这些都是你们的猜想，到底能不能实现，我们还需要实验来验证。

出示实验要求：

（1）两人合作，制作双面镜。

（2）放置积木，观察怎样使虚像个数更多。

（3）与同桌交流你的发现。

3.验证猜想，反馈交流。

师：做了刚才的实验，你有什么发现吗？

生：双面镜夹角变大，虚像个数变少；夹角变小，虚像个数变多。

师：看来刚才的猜想是正确的，增加1面镜子再调整角度大小，真的可以使虚像个数变多了。

【设计意图】以任务驱动的形式调动学生视觉、触觉等多重感官，初步发现夹角与虚像个数的关系，为进一步探索“夹角与虚像个数的函数关系”铺垫操作性思维经验。

4.使用角度卡，探索规律。

（1）观察个例，探索发现。

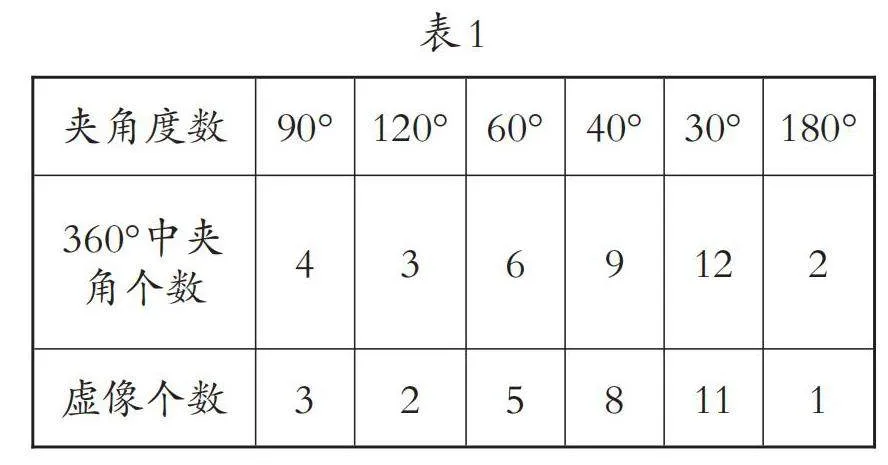
师：我们一起来观察一位同学刚才做实验时的照片（如图1），对着正中间这条线看过去，你能看到几个虚像？（生：3个）那实物在哪里？（学生指一指）猜猜这2面镜子的夹角是多少度。

生：可能是60°、90°或120°。

师：请拿出角度卡，动手试一试。

学生操作验证发现：夹角为90°。

（2）小组讨论，再次设疑。

师：看来这3个虚像和90°有一些关系，为什么偏偏夹角是90°的时候会出现3个虚像呢？小组讨论一下吧。

反馈学生讨论的结果。

生：镜子里有3个直角，每个都对应1个虚像。

生：1个周角是360°，里面恰好有4个直角，而其中1个是实像，所以虚像有3个。

师：如果4个夹角就会有3个虚像，以此类推的话，5个夹角、6个夹角又会产生多少个虚像呢？请继续用角度卡来验证你的猜想。

（3）列表归纳，建立模型。

出示学生操作过程，如图2。

师：将实验结果填入表格中（如表1）。请思考虚像个数与夹角度数有什么关系。

生1：我发现虚像个数每次都比夹角个数少1。

生2：当夹角是120°的时候，虚像个数=360°÷120°－1=2。

生3：当夹角是60°的时候，虚像个数=360°÷60°－1=5。

生4：以此类推，我发现夹角个数可以用360°÷夹角度数来计算。那么，虚像个数=360°÷夹角度数－1。

师：为什么每次都要减去1个？

生：因为有1个是实物。

师：如果夹角是30°，不做实验，你能计算出虚像个数吗？

生：360°÷30°-1=11（个）。

师：如果夹角是180°呢？怎么只有1个虚像呢？

生：360°÷180°-1=1（个），当两面镜子摆成180°的夹角时，相当于连接成了1面镜子，所以是1个虚像。

师：这就相当于我们最开始拿着单面镜照自己，只看到1个虚像。

【设计意图】从夹角为90°时虚像个数为3这一特例出发，学生初步发现虚像个数与夹角角度之间的关系，再运用类比推理，提出“虚像个数与360°中夹角个数之间相差1”的猜想。组织学生继续探究120°、60°、40°等角度，从特殊到一般，不断积累经验，通过不完全归纳，发现夹角与虚像个数之间的函数关系，借助实验实现学科知识到学科实践，又从学科实践到学科知识的双向整体联系，经历了一次数学建模过程。

三、拆解万花筒，拓展应用[ ]

1.联系实际，揭秘平行镜。

师：如果两面镜子面对面平行摆放会怎样？试一试。

生：会产生无数个虚像。

师：为什么有无数个虚像？可以用刚刚发现的算法来解释这个现象吗？

生：虚像被连续互相反射，产生了无数个虚像。

生：从刚才得出的公式计算：虚像个数=360°÷夹角度数－1，当夹角无限小的时候，虚像个数就无限大。

师：解释得非常好，有一些导演和特效师根据这一原理，制作了很多让我们叹为观止的视觉特效，让我们一起欣赏。

播放影片《盗梦空间》中“镜子时刻”的片段。

2.首尾呼应，了解原理。

师：现在大家再来猜一猜，万花筒里面究竟有多少面镜子？可以拆开来观察一下。

生：哇！里面居然有3面镜子。

师：明明是平行镜下才会有无数个虚像，里面没有相互平行的镜子，怎么也会有无数个虚像呢？

生：每两面镜子的夹角都是60°，每个60°都会产生多个虚像，虚像再经过多次来回反射后，形成无数个虚像。

师：两面平行镜就可以有无数个虚像，万花筒为什么还要选择三面呢？

生：因为万花筒是圆柱形，如果用平行镜，转动起来，会有一些角度不方便观察到虚像。

师：同学们真厉害，万花筒里的数学奥秘也被你们破解了！

【设计意图】用数学知识解释多面镜成像原理，发现两面平行摆放的平面镜能产生无数个虚像，并被广泛应用。以首尾呼应的形式，回顾释疑万花筒里镜子数量的猜想，在学生心中埋下实验研究的种子。

（作者单位：浙江杭州市天长小学）