亲历三门问题，提升“三会”素养

“设计和选用学习材料要彰显思维价值”，在浙江省新思维教育科学研究院，张天孝老师、朱乐平老师一直这样强调。三门问题是一个非常反直觉，但恰恰能彰显数学思维力量的学习材料。那么，如何促进学生从直觉判断向理性分析转化？基于实验数学的视域，我们的实践方式是“数学动手创”。面对现实问题，不停留于直觉判断，而是把它作为猜想，让学生经历实验操作、观察分析、推理论证等过程，体验像数学家一样思维，“创造”出属于自己的知识和见解，从而提升“三会”素养。

【三门问题简介】

三门问题得名于美国著名主持人蒙提·霍尔在1968年主持的一档“Let’s Make a Deal（一锤定音）”电视节目。在活动现场，有三扇门，其中一扇的后面有一辆汽车，另外两扇门后面则各藏有一只山羊，选中汽车者可当场开走。在现场，参与嘉宾首先选定一扇门，节目主持人是知道结果的，但他不是马上开门验证，而是开启剩下两扇门中有山羊的那扇门。面对剩下的两扇门，主持人紧接着问嘉宾：现在你想要改变选择，还是坚持原来的选择？

很多人认为，汽车停在门后没有移动过，改变选择不会改变结果，如果改变原来的选择，说不定“煮熟的鸭子飞跑了”，让人懊恼呢；但是不改变，会不会和巨奖就此“擦肩而过”，让人更遗憾呢？巨奖吸引人，选择很纠结，怎么办？如何做才能克服“跟着感觉走”的冲动，进行理性思考并做出正确的判断呢？

【教学目标】

1.用数学的眼光观察和思考一个综艺节目，学会转化成数学问题，把直觉判断作为猜想假设。

2.用数学的思维思考三门问题，通过模拟实验，以枚举和推理相结合的方法分析实验结果，发展推理能力。

3.用数学的语言表达三门问题的思考结果，有理有据地阐述自己的观点。

【教学过程】

一、观看节目，尝试用数学的眼光发现问题

（一）大屏幕呈现：“坚持”与“改变”。

师：同学们，当碰到一个让你为难的选择时，你是会坚持呢，还是会改变选择呢？

生：要看什么情况，能坚持的话，我会坚持下去。

生：我认为做这件事情比较有意义的时候，会坚持，但是如果我认为这件事情做不下去时，就会改变。

师：如果请你来参加有奖竞猜，选对就有一份巨奖，你会怎样选择呢？

（二）播放三门问题的节目视频：一锤定音。

（播放到第一次选择时暂停）

生：我会选3号门，我觉得主持人会把汽车停在最后一扇门后面。

生：我选2号门，和做选择题一样，选中间的更有可能对。

生：我觉得汽车停在三扇门后的可能性是一样的，都是[1/3]，选哪扇门都一样，我选1号门。

师：大家都同意吗？哦，大家都认同你的分析。让我们接着看。

（继续播放视频：主持人没有立即验证嘉宾的选择，而是打开了一扇门后无车的门，面对剩下的两扇门，让嘉宾再次选择）

师：同学们，现在主持人已经帮你排除了一扇门，如果你有机会再选一次，你会怎样选？为什么？

生：我和第一次相同，选择3号门，因为汽车没有动过，不管选几次还是在原地。

生：我和第一次相同，还是1号门，剩下的两扇门后都有可能有车，可能性都是[1/2]，既然相同，那我就不换了。

生：我想换一下选择，既然剩下的可能性都是[1/2]，那换一下选择说不定会让人惊喜呢。

生：我也想换一下选择，主持人这样做总有道理的吧。

生：才不换呢，主持人是故意的！他是故弄玄虚，引你上当。你想啊，如果你开始是猜错的，他为什么会让你再选从而得奖呢？

【教学随感】三门问题之所以令人感到反直觉，是因为人类面对不确定事件时不擅长处理。学生的选择，看上去有理有据，实际上和问题本身没有逻辑关系，只是在凭借原有经验下结论。不仅是学生，我们成人也常常囿于经验或直觉，不注意甄别现有的事实和原有的经验之间的差异，而用“经验代替事实”，然后开始“有理有据”地下结论。

师：现在我们统计一下。（统计结果是：40人中，坚持原来选择的有37人，改变选择的有3人）3位同学选择了“改变”，你们有没有什么想说的？

生：第一次有三扇门，选到的可能性是[1/3]，第二次剩下两扇门，选到的可能性是[1/2]，可能性增加了，所以我想换个选择。

生：其实是一样的，剩下两扇门不管怎样选择，可能性都是相同的，换不换选择结果都一样，就看运气好不好。

（教师当场统计，有这样的想法的学生有22人）

师：好，大家说了自己的想法。（板书：想法）不过，这是不是事实呢？（板书：事实）我们的想法和事实有没有差距呢？怎样来验证？

二、模拟实验，见证事实，用数学的眼光思考实验结果

（一）设计实验，模拟尝试。

师：大家都想亲自来尝试一下，看看自己的选择能不能得奖，是吧？我们来试一试。

【教学随感】如果实验课能有1小时的时间，教师还可以和学生共同讨论如何做模拟实验。在本节课中，教师是用倒扣在桌上的纸杯代替关闭的门，杯中放小玩具车（小球）。在实验之前，还有一个细节需要考虑：主持人放小玩具车（小球）时怎样才能做到随机摆放？因为如果不是随机摆放，主持人由自己的心意摆放，那么这个活动就变成了猜主持人心思的活动了。

师：如果你是主持人，你会把小车放在哪个杯子里呢？

生：我会轮流放，每次放的位置不一样。

生：我想每次放同一个位置，因为猜的人以为我每次都会换地方放。

师：那你们的好朋友来猜，事先知道你们的习惯，正确率比别人更高了吧。这样就会——

生：不公平！

生：最好再请一个人来放小车，这样大家都看不到。

生：如果都看不到的话，那主持人等会儿还要翻开一个空杯子啊……

师：以前我们玩游戏时，为了保证公平，是用什么方法？（生：掷骰子）为保证公平，待会儿主持人就用掷骰子（本实验用的是“三数骰子”，它只有3个数，6个面上分别是2个“1”、2个“2”、2个“3”）看点数的方式决定小车放哪个杯子里。现在谁愿意来试试？

（教师请2个学生分别扮演主持人和嘉宾来模拟活动，让大家熟悉实验过程）

（二）模拟实验，观察记录。

师：大家是不是都想自己来做？同桌两人讨论一下，怎样做这个实验呢？

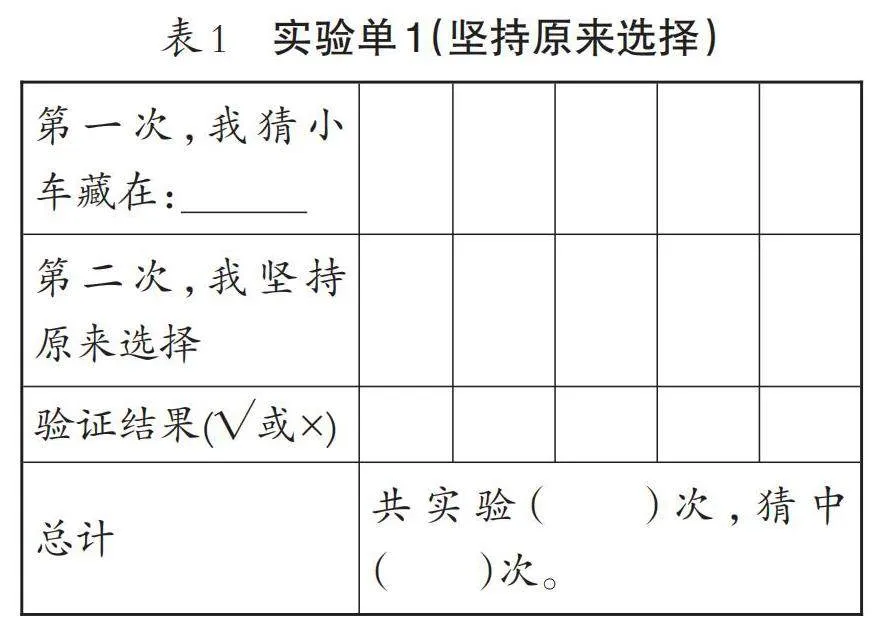
讨论后反馈：同桌两人互做主持人与嘉宾，把实验结果分别记录在实验单1（坚持原来选择，如表1）、实验单2（改变原来选择，实验单略）上。视时间，每人不少于5次。

实验签名：_________。

三、审视数据，用数学的思维解析成因

（一）实验反馈，汇总数据。

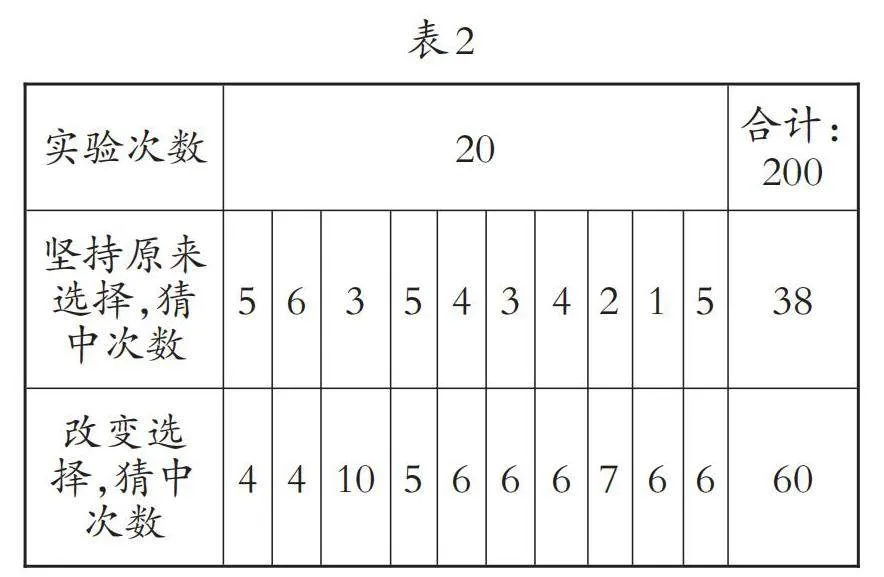
由于时间关系，这节课每人实验了5次，同桌活动后汇总到四人小组，数据如表2。

（二）审视数据，交流讨论。

师：这是我们刚才实验中产生的数据，同学们有什么想说的？四人小组讨论一下。讨论后，全班交流。

生：我发现改变选择后得奖的次数更多一点。

生：这个数据是有误差的，应该是一样的，因为剩下两个杯子，选中的可能性是一样的。

生：我觉得不一样，从表格中的数据看，虽然有2组“坚持原来选择”的得奖率高，只高了一点点，但是有8组都是“改变选择”得奖率高（有1组得奖率是相同的），全班汇总也是“改变选择”的得奖率高，高好多。

师：从全班的数据看，“改变选择”后成功的有60次，大大超过了“坚持原来选择”的38次成功。如果继续实验下去，还是“改变选择”成功率高吗？其中有没有什么奥秘呢？

（学生议论纷纷，有的拿起杯子放慢动作一边做一边想，有的拿起笔写写画画）

生：我觉得不一样，坚持原来选择的获奖可能性是[1/3]，改变选择后获奖可能性是[1/2]。

生：不一样，猜中一个杯子的可能性是[1/3]，另外两个是[2/3]，那么翻开其中一个空杯，另一个杯子里面有小车的可能性是[2/3]。

四、多元表征，用数学的思维解析成因

师：大家能听懂吗？（不少学生摇头）怎么说别人才容易听懂呢？（这个学生又重复了一遍）现在同学们能理解吗？（大部分学生还是摇头）我们是不是可以举个例子试试看？

生：比如，如图1，第一次选择了1号杯，小车在里面的可能性是[1/3]，在另外两个杯子里的可能性是[1/3]+[1/3]=[2/3]。大家同意吗？（学生点头）现在翻开了这两个杯子中的一个，没有小车，可能性是0，那么在另一个杯子中的可能性就是[2/3]。

师：大家同意吗？有问题想问吗？

（学生若有所思）

生：如果第一次选择2号杯呢？

师：是啊，也能这样想吗？如果第一次选择3号杯呢？我们能不能用画示意图的方法来分析？同桌交流交流。

【教学随感】学生用画示意图的方法分析，发现“翻开空杯”这个举动很关键，排除了这只杯子的可能性，增加了另一只杯子的可能性。学生借助图形，容易发现事物之间的联系和变化，有助于发现问题解决的思路，有利于发展几何直观。

师：看来，画示意图能让我们更容易发现问题中的关系，帮助我们解决问题，真是个好方法！在平时的数学应用中，我们还常常用到哪些方法？比如用表格来分析，我们能试试吗？

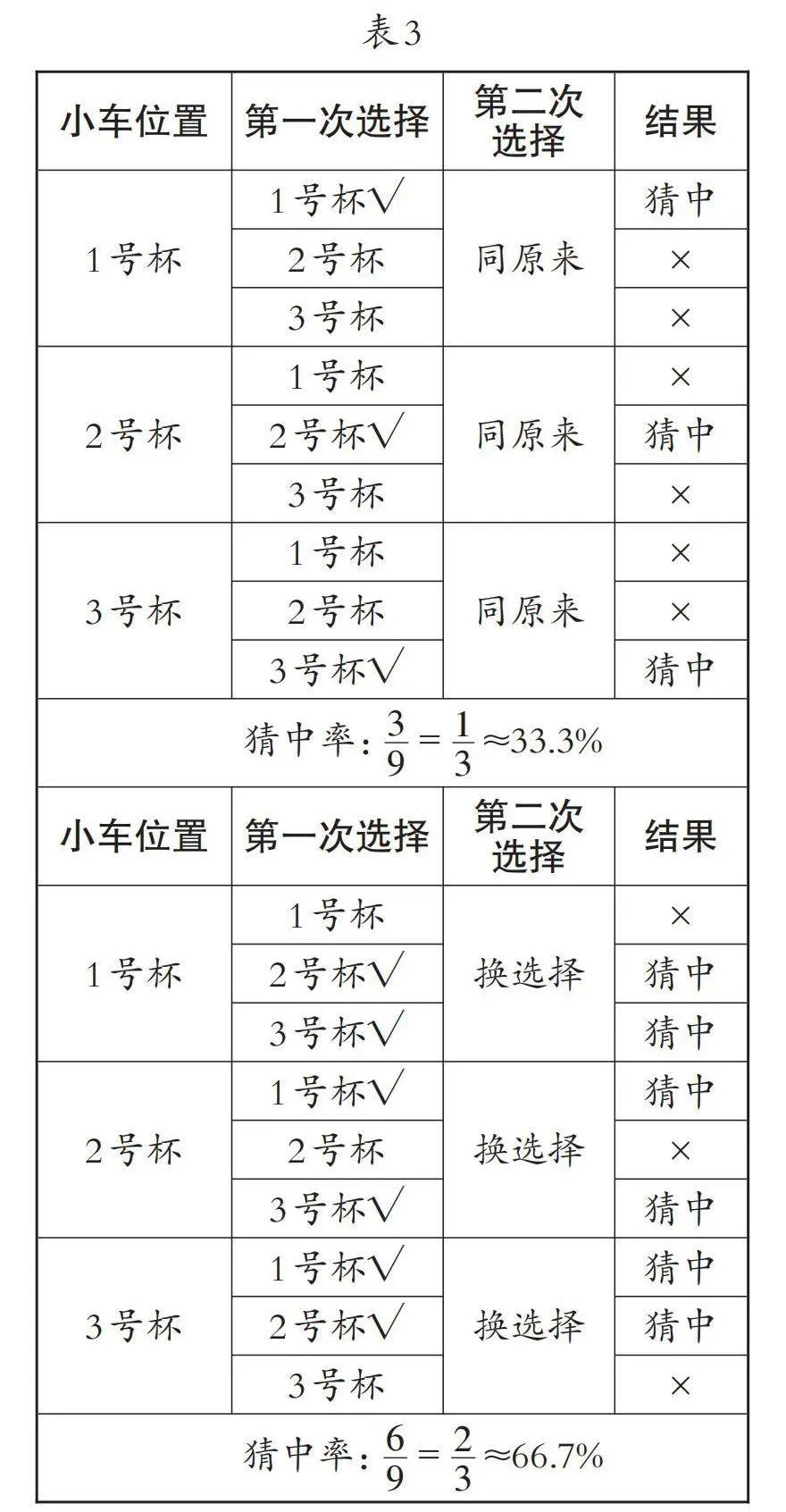
（学生反馈，在表格中把可能发生的情况列出来，如表3）

师：从表格中，我们可以发现什么？如果坚持原来选择，要在什么情况下才会猜中？

生：明白了，只有在第一次就猜对的情况下，坚持原来的才会猜中，可能性是[1/3]。

生：如果第一次猜错，那就要改变选择才会猜中，原来错的可能性是[2/3]，改变后变成猜中，所以改变选择后猜中率是[2/3]。

师：是这样吗？同桌互相检查一下。看来，××同学的发现是正确的。刚才我们用表格来分析，你觉得有什么好处？

生：我发现用表格来分析，可以把每一种情况都写出来，方便我们看。

生：我发现在用表格描述的时候，排列更有序，这样更能看出规律。

师：是呀，刚才我们用了列表法分析，还有之前用的画示意图法等，这些方法都能帮助我们整理信息，发现问题，找到关键，从而有理有据地分析。

五、回顾反思，提升认知

在经过问题猜想、实验设计、实践操作、观察记录、分析解释这一系列实验步骤之后，学生得到了三门问题的初步解答，接下来是实验教学的重要一环：回顾反思。在整个回顾反思环节，教师提醒学生回顾与思考。

师：同学们，今天这节课就要结束了，让我们来回顾一下吧！

屏幕上显示：

（1）今天的实验最让我开心的是（ ）。

（2）今天的实验最让我惊讶的是（ ）。

（3）今天的实验中我遇到的困难有（ ），我的解决方法是（ ）。

（4）今天的实验让我又冒出了一些新问题：（ ）。

生：最让我开心的是玩。最让我惊讶的是我以为可能性是一样的，没想到换选择后赢的可能性更大。

生：我一直以为坚持原来选择赢的可能性更大，做事情要坚持嘛。没想到改变选择后赢的可能性更大。

生：通过今天的活动，我想如果杯子更多，怎么选？会有什么规律呢？

生：今天的实验只有1辆小车，如果有100扇门，小车不止1辆，比如3辆，这个游戏该怎么玩？

生：如果主持人自己也不知道汽车放在哪扇门后面，随意打开一扇门，那怎么选呢？

师：今天的活动同学们玩得都很开心，很有收获，我们还想到了许多新问题，特别好！大家不妨选择其中感兴趣的问题继续研究。

【教学随感】这个回顾反思的过程是我们在所有数学实验教学中都要进行的。与反思框架中的其他问题相比，我们在本课更重视框架中的问题（1）和问题（2）的反思。在讨论中，学生们表达了自己的实验感悟：“实验前，我以为……实验后我发现……”“在实验中，我发现结果和我之前想的不一样，画过表格以后，我才发现原来……”通过反思，学生们的思维虽然还不能完全抽象到数学层面，但让他们体验到直觉的优势和理性的力量也正是本节课的重要目标。

（作者单位：罗永军，浙江省新思维教育科学研究院，杭州市胜利山南小学；沈建琦，杭州市青少年活动中心）