实践验证结论探

作者简介：赵向荣（1978—），本科学历，中学一级教师，从事初中数学教学与研究工作.

[摘 要] “三角形的内角和”作为苏科版七年级下册的内容，与小学知识衔接紧密，其中的内角和定理是几何推理的重要依据. 教学中教师要注重论证过程，设计丰富的活动，引导学生探究论证. 文章围绕定理核心，开展说理论证，探讨教学实践.

[关键词] 三角形;内角和;定理;证明

三角形的内角和是初中数学三角形部分的重要内容，是后续角度推理、计算的依据. 学生在小学阶段通过观察操作已经了解到三角形的内角和为180°，而初中阶段教学的重点是探索证明三角形的内角和定理，即引导学生从感性认识上升到深层的理性认识. 因此教学的重点是关于定理的推理与证明过程，下面开展教学探讨，探究活动设计.

设计丰富活动，引导学生认知

“三角形的内角和”章节知识衔接了小学与初中知识，同时学生已经掌握了三角形的相关知识. 关于三角形的内角和定理教学，教师可以从如下两方面来引入：一是直接给出三角形，让学生回顾三角形内角和的度数，唤起旧知;二是展示实际问题，让学生提出解题思路，具体如下.

1. 知识回顾，调动旧知

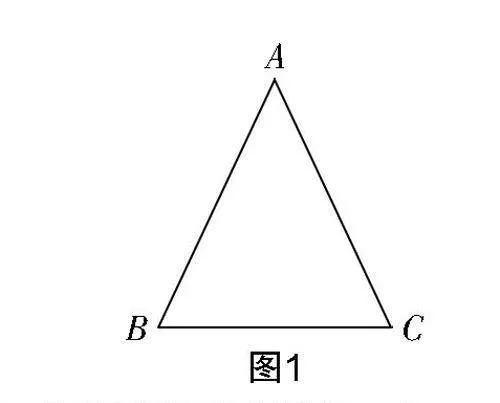
如图1所示，△ABC是我们所熟悉的三角形，那你们还记得三角形的内角和是多少度吗？

设问：对于三角形内角和的结论，大家有哪些证明方式？

学生在小学阶段通过裁剪、拼接得到了“三角形的内角和为180°”这一结论，教学中教师可以引导学生回顾此方法，通过小组讨论，展示更多的拼接方法.

2. 实例引入，启发思考

问题：如图2所示，在△ABC中，∠BAC=40°，∠B=75°，AD是△ABC的角平分线，求∠ADB的度数.

设问：求∠ADB的度数时，具体的求解思路是什么？请说理理由.

教学引导：根据已知条件，我们可以得到，在△ADB中，∠B=75°，∠DAB=20°，所以需要借助三角形的内角和来进行计算. 此时教师可以引导学生思考求解依据，从而引出三角形的内角和知识.

立足学生的知识起点构建新知，唤醒学生的认知，可以充分调动学生的探究热情. 在教学中，教师要注重说理引导，即让学生思考如何证明，为后续的推理探究做铺垫.

实践探究说理，完成定理证明

三角形的内角和定理是初中几何重要的定理，对于定理的说理教学，建议教学时分三个阶段来开展：第一阶段，直观的几何感知;第二阶段，实践几何体验;第三阶段，严谨的几何论证.

1. 直观感知

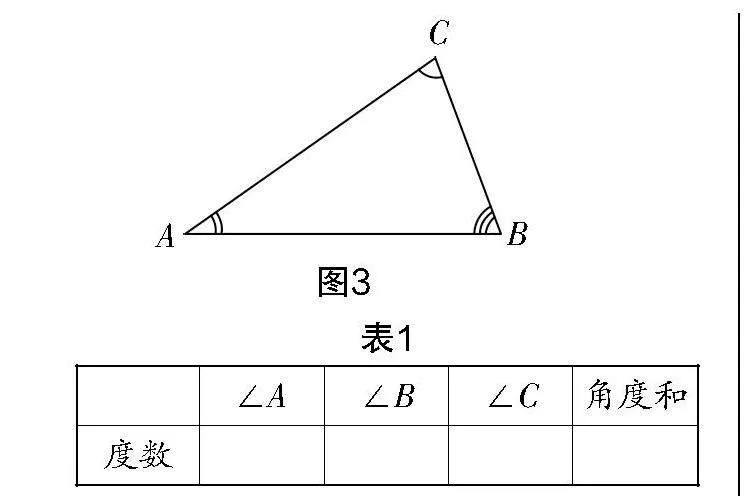
“直观感知”环节需要教师引导学生观察图形，初步做出判断. 故教学中学生可借助量角器来测量角. 如教师给出如图3所示的△ABC纸板，让学生用量角器分别测量三个内角，计算角度之和，并完成表1.

实际测量是验证三角形内角和最为直接的方法，学生可直观感知结论，但测量存在误差，教学中教师要注意引导学生小组交流，共享结论并做出判断.

2. 实践体验

“实践体验”环节可同样借助纸板裁剪拼接的方式，让学生通过动手操作来做出准确的判断. 当然，学生拼图的方式存在一定的差异，教学中教师要引导学生进行对比思考.

活动：请将如图3所示的△ABC的三个内角撕下，然后将三个内角的顶点拼接在点B处.

设问：（1）所形成的新角的两边是否在同一条直线上？你有何猜想？（2）拼图的本质是什么？

实践操作时，学生可能会拼出如图4所示的两种图案. 教学中，教师要引导学生关注pvBjQ+rMOeWapGJbvMOBww==新角的两边在同一条直线上，故可验证三角形的内角和为180°. 教师还可以让学生在任意顶点处进行拼接，从中获得启示. 此外，教师要注意引导学生关注拼图的本质，即三角形内角的等角转移，在平面内的同一点处构成平角.

3. 严谨论证

“严谨论证”环节需要教师引导学生用数学的公式定理、方法思路来加以证明. 该环节同样需要依托上述裁剪拼接实验，通过作辅助线、设点的方式来构建模型，实现问题的数学化. 故教学中教师要引导学生作辅助线，把握图形的关键点，并进行逻辑推理.

活动：根据图4来作辅助线，并设定新角的顶点，作出如图5所示的数学模型. 思考图5模型中有哪些等角，如何证明三角形的内角和为180°.

教学时教师要引导学生从拼图中获得等角关系，再借助模型中的平角推得结论. 基于图4所示的两种方案，学生可以得到对应的图形，根据图形特征即可进行证明. 教学时教师可针对图5引导学生逐个分析.

证法1：如图5①所示，过点B作AC的平行线EF. 因为AC∥EF，所以∠CBF=∠C，∠ABE=∠A. 因为∠CBF+∠ABC+∠ABE=∠EBF=180°，所以∠C+∠ABC+∠A=180°，即△ABC的内角和为180°.

证法2：如图5②所示，延长AB至点E，再过点B作BF∥AC. 已知BF∥AC，所以∠CBF=∠C，∠FBE=∠A. 因为∠ABC+∠CBF+∠FBE=∠ABE=180°，所以∠ABC+∠C+∠A=180°，即△ABC的内角和为180°.

上述针对剪裁拼接构建了数学模型，利用几何的分析方法和思路构建了证明过程，教学中教师要引导学生关注过程中的逻辑关系和推理步骤，即由“图案”抽象“模型”，由“特性”提取“条件”，由“已知”推导“未知”，过程分析要有理有据.

以上述“证法2”的推理过程为例，教师要让学生针对每一步进行说理，使学生充分理解其中的数理逻辑.

第一步，延长AB至点E，再过点B作BF∥AC——作图过程.

第二步，已知BF∥AC——作图所得.

第三步，可得∠CBF=∠C——两直线平行，内错角相等;∠FBE=∠A——两直线平行，同位角相等.

第四步，因为∠ABC+∠CBF+∠FBE=∠ABE=180°——平角的定义.

第五步，所以∠ABC+∠C+∠A=180°——等量代换.

开展多样实践，实现结论一般化

三角形的内角和定理是几何中的重要定理之一，在前面的教学过程中，教师引导学生通过拼图推理完成了证明，但从探究过程来看，并不具有一般性，学生很容易产生“是否其他三角形的内角和不符合180°”“三角形中边的长度变化是否会影响其内角和”等疑惑. 故实际教学时，教师有必要设计丰富的探索活动，让学生深入感悟三角形的内角和定理. 实践教学时建议教师从如下两方面来进行探究：一是对三角形进行拼接组合;二是改变三角形中边的长度.

1. 叠图组合，一般性探究

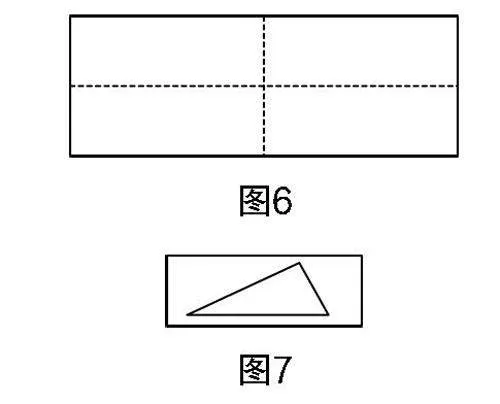
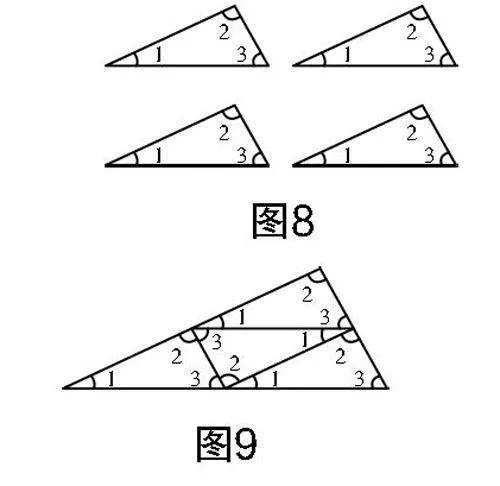
活动：将一张长方形纸片按照图6所示的方式对折两次，再在纸片上绘制一个一般的三角形，如图7所示，剪下后可获得如图8所示四张形状、大小相同的三角形纸片.

思考：用图8所示的四张小三角形纸片能否拼成一个大的三角形？这个大的三角形的内角和是否依然是180°？请说明理由.

教学引导：教师引导学生将四张三角形纸片按照图9所示的方式拼接. 由于四张三角形纸片完全相同，故其内角相当于由四张小三角形纸片的内角组合而成，从而使学生感知到任意三角形的内角和均为180°.

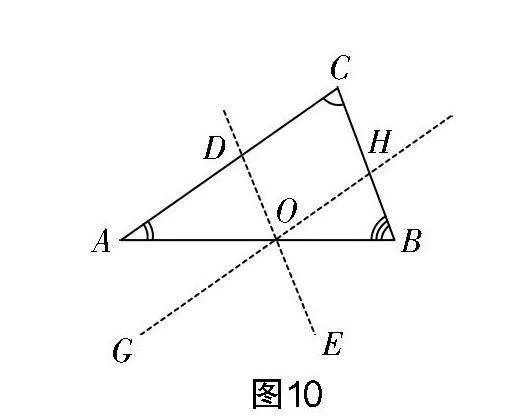
教学中教师可引导学生根据上述组合思路来作图，即过△ABC三边上任意一点作另外两边的平行线，将三角形的三个内角转移到顶点均在边上的一点处，从而构建平角，如图10所示. 探究验证时，教师可利用平行线的性质来等角转化，使学生感知到：任意三角形的三个内角均可以构建平角，即任意三角形的内角和为180°.

2. 动态探索，拓展性思考

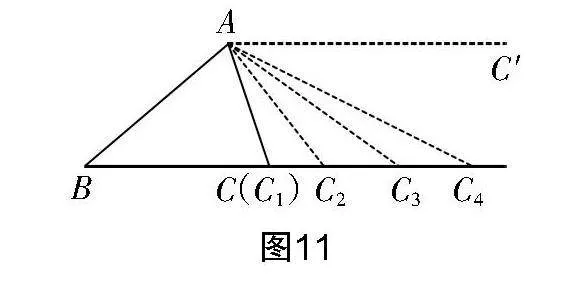
如图11所示，△ABC的边AC所在直线绕点A逆时针旋转，旋转过程中射线AC与射线BC分别交于点C1，C2，C3，…

设问1：在直线AC的旋转过程中，三角形的哪些内角大小发生了变化？

设问2：度量∠BAC1和∠AC1B并求它们的和，度量∠BAC2和∠AC2B并求它们的和……大家有什么发现？

设问3：当直线AC绕点A旋转到与直线BC平行时（即旋转到图11中的AC′位置时），度量∠BAC′的度数，大家有什么发现？

教学引导：教学中教师引导学生关注旋转过程中，三角形的两个内角变化，即∠BAC逐渐变大，∠ACB逐渐变小，但两角之和始终保持不变. 而当直线AC绕点A旋转到与直线BC平行时（即旋转到图11中的AC′位置时），∠BAC′的度数与前面两角之和相等.

对于动态变化中三角形的内角和为180°这一结论的证明，教师可以采用几何推理的方式，即当AC′∥BC时，有∠CAC′=∠C，∠BAC′+∠B=180°. 因为∠BAC′+∠B=∠BAC+∠B+∠C，所以∠BAC+∠B+∠C=180°，从而完成证明.

用运动变换的观点来探究证明三角形的内角和，更贴近实际，演绎推理合情合理. 旋转过程中三角形的内角会发生变化，但结论一致，这能让学生更加深刻地体会定理. 同时，这种探究方式可以帮助学生积累探究经验，培养数学思维.