顶角互补的双等腰结构的基本研究 与一般化推广

作者简介：周道碧（1969—），本科学历，中学高级教师，从事中学数学教学研究，2021年主研市教育学会重点课题“城市初中学校减负有效策略研究”，结题并被重庆市教育学会评为特等奖.

[摘 要] 在几何证明中，对本质结构的研究能极大加强对新结构的认知，本质结构通常称为一般化结构. 通过挖掘几何图形的本质结构，能快速解决一系列问题并加深对条件相互作用的理解. 本文以一道中考模拟题为研究的起始点，展开对顶角互补的双等腰结构的研究与一般化推广.

[关键词] 顶角互补，本质结构，一般化

《义务教育数学课程标准（2022年版）》是基础教育和课程改革的方向，相较于2011年版，新课程标准以学生为主体，对加强学生创新意识的培养提出了更高的要求. 新课标对学生数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想等方面的培养制定了更细腻的目标，切实符合义务教育阶段的数学教育与教学. 在双减背景下，减负提质，对几何题目多种证法的剖析推广的研究，能使学生有更强的图形感. 不断加强对几何直观的培养，提升学生演绎推理的能力，才能真正达到提质的目的.

原题呈现

如图1所示，在△ABC中，AB=AC，∠BAC=120°，点D为直线AC右上方一点，且满足∠ADC=60°，连接BD.点E为线段BD上一点，连接EA，EC，且满足∠EAD=60°，证明：AD=CD+2AE.

结构分析

对任意几何题目，通常会从基本结构与角度两方面进行分析，其中对角度等量关系的挖掘，可以更加充分地加强对题目的理解. 在本题中，题目的背景是等腰三角形ABC，等腰三角形有一组相等的线段，由这组等线段，经常会从旋转与对称两种全等变换中去考虑对线段角度的转化. 结构的等价变形也会加深对几何结构的辨析与理解.

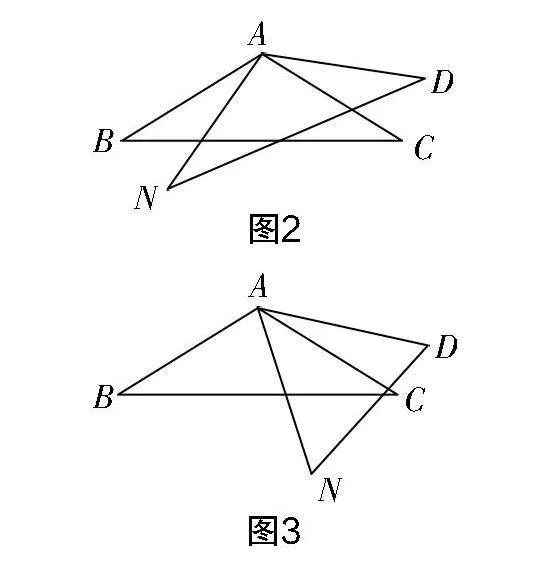
1. 旋转形构造

本题已知有两个60°，便于构造旋转形，旋转结构优先考虑.

从结构与角度分析，如图2，图3所示，会有如下两种旋转构型. 结构一可以转化CD，结构二关联了已知的两个60°，同时均有补基本形的特点.

从结论分析，待证结论中的2AE实则也包含了解题的构造方向. 二倍关系的处理通常会归结为中点问题，倍长中线，中位线，斜中半，三线合一是思考的基本方向.

2. 提炼等价构图

在相同的背景条件下，通过旋转△AED，保证点D，E，C共线，即可得到本质相同的不同构图，如图4所示，对原题的研究，可转化为对其等价构图的研究.

题目解析

1. 结论结构齐步走，倍长补形显身手

证法1：如图5所示，延长AE，DC交于点M，过点D作DF∥AB交AM于点F，交AC于点G.

证明简述：由DF∥AB，可知∠AGF=60°，可得∠CAD=∠FDE，因此△ACD≌△DFM，所以DF=AC=AB，可证得△AEB≌△FED，所以2AE=AF，因此AD=CD+2AE.

分析 从结论结构同时出发，由2AE考虑倍长中线，通过关联60°考虑补等边三角形AED，由此产生基本构图，在解题中考虑补形是关键.

2. 找准基准三角形，转移线段补结构

证法2：如图6所示，延长AE，DC交于点M，在MD上取点F，使得MF=AE，连接AF.

证明简述：由MF=AE，AM=AD，∠DAE=∠AMF，可得△DAE≌△AMF，所以∠DEA=∠AFM，∠ADE=∠FAC，可知∠AEB=∠AFC，设∠ADE=α，∠FAC=β，∠ABD=θ，在△ABD中，∠ABD+∠BAC+∠CAD+∠ADB=180°，可得θ+120°+60-α-β+α=180°，即θ=β，因此△BEA≌△AFC，所以AD=CD+2AE.

分析 基于CD的位置，AE所处的基准三角形，最终在MD上完成了线段和差关系的证明，此种处理方法的关键在于AE的基准三角形有两个，AE既在△ADE中，也在△ABE中，因此2AE最终理解为搬动两个基准三角形.

3. 先猜后证线加倍，旋转补短方向准

证法3：如图7所示，延长AE，DC交于点M，延长BA至点F，使得AB=AF，连接FD.

证明简述：易证△ADF≌△AMC，可得∠AMC=∠ADF=60°，所以∠EAD=∠ADF，因此AE∥DF，又由AB=AF，所以BE=ED，AE为△BDF的中位线，因此2AE=DF，所以AD=CD+2AE.

分析 从几何直观出发，可推测点E为BD的中点，若点E为BD的中点，则2AE=DF，即可完成2倍AE的构造与转换，此法的关键在于间接构造基本结构.

4. 解法共鸣，本质相通，提出猜想

由这三种证法的特殊性，笔者开始分析与关联一道证法相似，结构相似的题目，可由此进行类比.

题目为：如图8所示，已知△ABC，△BDE均为等腰直角三角形，连接AD，CE，过点B作BG⊥CE于点G，GB交AD于点F，求证：2BF=CE.

上述题目依然可围绕倍长中线、中位线等思路展开证明，由于证法相似，不作说明. 据此，研究两道几何题的结构共性即可提炼出一般化结构，从而得到一般化结论. 从题目背景来看均为双等腰结构，区别在于顶角的大小，但两个等腰三角形的顶角之和均为180°，同时具有2倍关系的线段在两道题目中有着相同的位置，由此可得到如下猜想.

猜想：如图9所示，在顶角互补的双等腰结构的背景下，即AB=AC，AE=AD，∠BAC+∠EAD=180°，点N，F分别为BE，CD的中点，可推得如下结论：

①2AN=DC，2AF=BE;

②△AFC≌△BNA，△AFD≌△ENA;

③S=S.

5. 验证猜想，一般化推广

由于△ABE与△ACD具有等价性，不妨证明2AF=BE，同理可证得2AN=DC. 因猜想的结构为一般化结构，可尝试用相似方法进行证明.

证法：如图10所示，过点C作CG∥AD交AF的延长线于点G.

证明简述：由点F为CD的中点，易得△FDA≌△FCG ，所以AD=CG，由CG∥AD，∠BAC+∠EAD=180°，可得∠ACG=∠EAB，因此△EAB≌△GCA，所以AG=BE=2AF，上述猜想结论可由此继续展开而得到验证.

通过中位线与直接构造也可完成猜想结论的证明，图9所示的基本结构即为一般化结构. 从证法，结构，待证结论产生基本感知，从不同结构中提炼出相同的基本要素，是一般化推广的基本方式. 从一般化结构再回到特殊结构，即完成了从一般到特殊的转化，此时对特殊结构的认知会更加深刻.

6. 探中点产生根源，究相同本质条件

在原题与类比题目中，中点E与F的产生方式不同，原题为线段相交产生中点，类比的题目中为作垂直产生. 从一般结构出发，产生中点的条件的本质应是一致的.

在一般化结构中，△AFC≌△BNA与△AFD≌△ENA的全等一定存在，在原题中即为△DAE≌△AMF与△BAE≌△ACF. 将原题等腰三角形的顶角一般化，可设∠EAD=α，则∠BAC=180°-α，若点E为BD中点，则由△DAE≌△AMF，可得∠DAE=∠AMF，即α=90°-，解得α=60°. 因此，点E为中点实则是由等腰三角形顶角的限制得到，本质是∠EAD=∠AMF. 将结论推广，如图11所示，可得到更一般的构图，同样满足一般化的结论. 对图9所示的一般化结构，按照相同思路，如图12所示，若∠BAC=∠AMC，则点N为中点.

在顶角互补的双等腰结构中，中点的产生本质是由结论②中全等的对应角限制而得到，对产生中点的条件进行分析理解，其本质实则是相同的.

7. 基于一般化思维下的几何模型意识的认知

一般化思维是一种抽象思维方式，它能够将具体的事物或现象抽象成一般性的概念或规律. 在几何学中，一般化思维可以帮助我们更好地理解和探索几何图形. 一般化思维是人类认识世界的重要方式之一，它可以帮助我们更深入地理解事物的本质，并为我们解决问题提供有力的思维工具. 在几何研究中，用一般化思维解决问题的流程是从特殊到一般再回到特殊，理解一般化结构，会对特殊结构有更深刻的认识.

通常情况下，研究几何结构的关键是研究其基本结构、基本性质. 不断增强模型意识，才会对模型有更有充分的理解，建模能力才得以不断提升. 在传统的思维模式下，往往是特殊题型对应特殊结构，笔者认为在更一般情况下总结归纳会产生更好的效果. 同时在提取一般结构的过程中也是对抽象思维、逻辑思维、创新创造能力的培养.

参考文献：

[1]樊璐瑛. 初中生数学学习力提升策略研究[D]. 西南大学，2018.

[2]路明. 论数学形象思维能力的培养[D]. 辽宁师范大学，2011.