探索知识关

作者简介：夏恋（1981—），本科学历，中小学一级教师，从事初中数学教学与研究工作.

[摘 要] “三角形相似成立的条件”与“全等三角形的判定定理”有一定的关联，实践探究建议从全等出发，开展定理探索，设计丰富的实践活动，引导学生思考，拓展学生思维. 文章从知识关联的角度对“探索三角形相似的条件”进行教学设计.

[关键词] 相似三角形;知识关联;条件;定理

“探索三角形相似的条件”是苏教版九年级下册重要的内容，是几何“空间与图形”范畴的知识探究. 从整个知识内容来看，是对全等三角形知识拓展与发展，指导学生掌握三角形相似成立的条件，形成数学的思维方式和思想方法是教学的重点.

基于上述分析，实际教学中要理清三点：一是从知识的衍生与发展角度来探索相似成立的条件;二是从条件定理探索的过程思考教学设计;三是从应用强化角度思考学生思维能力的提升. 下面结合教学核心进行深入探讨.

知识关联探讨，全等衍生相似

教材将“探索三角形相似的条件”安排在“全等三角形”之后，学生在学习本章节知识内容时已经掌握了三角形全等的判定定理，并积累了图形的性质和判定的探究经验. 对于“X5hu0qLvt5wEFBTdKBylxQ==三角形相似的条件”的探索，需要把握两点：一是知识的关联性，二是知识链的完整性. 即注重知识关联，构建完整的知识链，从全等中衍生相似定理.

从教材内容设计来看，全等三角形与相似三角形之间存在一定的联系，可将三角形相似视为全等三角形的“弱化”，即从三角形全等判定定理中衍生三角形相似成立的条件，从而让新知的生成有理有据，逻辑关联性强.

教学推进中需要让学生回顾全等知识，思考两方面问题：

一是三角形全等判定定理有哪些？

二是如何将三角形全等判定定理进行弱化？弱化后是否可以判定三角形相似？

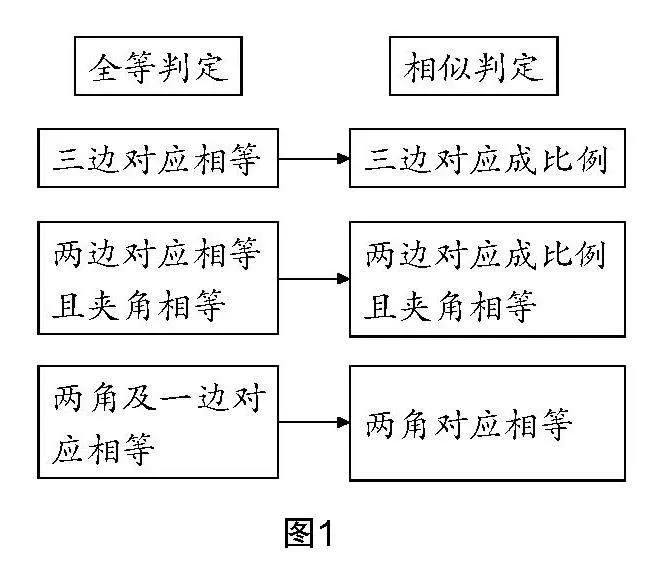
对于三角形全等的四个判定定理：SAS、ASA、AAS、SSS，从两大视角进行弱化引导：一除去其中的一组对应边相等;二是将其中的对应边相等，弱化为对应边成比例，如图1所示的弱化对应关系.

基于上述知识关联性、整体性开展的教学衍生推进，可以构建三角形相似成立的条件，实现“全等判定”向“相似判定”的转化.

经历探究过程，定理自然生成

“探索三角形相似的条件”章节内容本质上是探究三角形相似的判定定理，属于定理教学. 下面以三角形相似成立的条件“两边对应成比例及夹角相等”为例，开展教学设计，构建教学活动.

1. 情景引入，启发思考

学生已经掌握了三角形全等的判定定理，教学中弱化定理SAS来引出三角形相似成立的条件.

如图2所示，在△ABC和△A1B1C1中，已知AB=A1B1，AC=A1C1，∠A=∠A1，两三角形是什么关系？请说明所用的判定定理.

在△ABC中点D和E分别是AB和AC的中点，则△ADE与△ABC有怎样的关系？请说明理由.

思考：若要使△ADE演变为△A1B1C1，需要经过怎样的变化？

教学中从三角形全等的判定定理“SAS”入手，引导学生关注图形“缩放”后形成的相似关系. 同时“A”型相似图形的“叠放特点”有利于学生把握“对应边成比例”这一性质. 教学中注意对条件的罗列对应，直观呈现边的比例关系，可引导学生填写下表.

2. 活动体验，相似思考

活动一：请同学们准备一张三角形纸片，思考怎样剪可以获得一个与已知三角形纸片相似的三角形纸片，小组讨论，共享方案.

活动二：按照如下方案来裁剪三角形.

方案1：在已知的三角形上画一条边的平行线，沿着平行线截得三角形，再在纸片上画出与截得三角形全等的三角形，并剪下来.

方案2：先画一个与已知三角形中某角相等的角，再分别将该角的两边放大或缩小2倍，再将其剪下来.

方案3：如图3所示，先取三角形三边的中点，然后按图连接中点，再将中点三角形剪下来.

设问：思考三种方案所获得的三角形与原三角形是否相似？三种方案可以得到怎样的几何关系？

方案1：沿平行线裁剪→两边对应成比例

方案2：角的两边缩放→两边对应成比例

方案3：连接中点→两边对应成比例

活动三：在如图4所示的两个三角形中，已知∠A=∠A′，对应线段关系如图，是否可以判定两个三角形相似？

设问：请分别计算和的比值，可以得出怎样的结论？

3. 辨析说理，定理生成

该环节需要引导学生总结三角形相似成立的条件，生成定理. 同时引导学生开展辨析，探究定理的正确性.

辨析思考——以如图4所示两个三角形为例

设问1：若将条件“∠A=∠A1”去掉，两个三角形是否依然相似？

设问2：若将条件“∠A=∠A1”替换为“∠B=∠B1”或“∠C=∠C1”，两个三角形是否还相似？

定理生成——以如图5所示两个三角形为例

根据活动探究，引导学生陈述两个三角形相似成立的关系.

条件：在△ABC和△A′B′C′中，已知∠A=∠A′，=.

结论：△ABC∽△A′B′C′.

文字语言描述：两边对应成比例及夹角相等的两三角形相似.

应用迁移体验，能力强化提升

三角形相似成立的条件在解题中有着广泛的应用，教学中要开放探索、开放思维，让学生在应用迁移，思考探索中获得能力的提升. 问题设计建议由原型问题进行变式，由易到难，逐步深入，既注重定理强化，又有利于学生的思维拓展.

总之，“探索三角形相似的条件”的教学探究要基于内容的知识关联和整体性来开展，从三角形全等出发，探索三角形相似条件;让学生经历探究过程，深刻理解定理本质;合理设计应用问题，以提升学生的思维能力为重点. 整个教学环节，让学生的思想自由发挥，知识内化吸收.