基于解题经验培养的数学教学研究

作者简介：沈习辉（1977—），本科学历，中学高级教师，从事初中数学教学与研究工作，宿迁市数学骨干教师，宿城区数学学科带头人.

[摘 要] 建构主义理论认为问题的解决需以原有的解题经验为基础，在新旧问题之间建立联系是提升解题经验的法宝. 本文以“梯形”的解题教学为例，认为有效追问能帮助学生进一步理清解题思路，形成解题经验;引导学生经历尝试，可让学生在自主探索中验证经验的可靠性;及时总结提炼，可提升学生的解题经验，为形成触类旁通的解题能力奠定基础.

[关键词] 经验;追问;概括

实际教学中，有些教师将问题的正确答案作为教学的终点，教学过程因缺乏追问、拓展与总结，导致学生无法形成良好的解题经验，难以达到举一反三的解题能力. 为了改变这一现状，笔者对如何帮助学生形成良好的解题经验进行了大量的研究，发现解题教学从追问、尝试与总结三个方面出发，能起到较好的成效.

借助追问，形成经验

学贵有疑，追问属于创疑的一种方式. 适时追问可引发学生思考已经回答过的问题，让学生进一步理清解题思路与方法，为形成解题经验奠定基础. 但不少教师仅将目光锁定在原式问题的设计与处理上，忽略对问题的拓展与延伸，课堂常因缺乏追问导致无法达到深度学习的阶层. 这部分教师在学生回答问题后，直接给予肯定或否定，而不进行具体的评价，导致学生无法在自身原有的基础上得到更深层次的理解.

获得结论并不是最重要的，重要的是获得结论的过程. 追问对促进学生解题经验的积累具有重要意义，不论学生的回答是正确还是错误，作为一名合格的教师都应让学生阐述自己的想法，让学生通过对结论形成的追忆暴露真实的思维过程，以觉察思维方法的正确性.

事实证明，一个充满智慧的教师不仅能设计出精巧的问题，还能根据学生的答题情况与思路历程提出恰当的追问，达到促进经验形成的作用.

例1 如图1所示，在直角梯形ABCD中，AB∥DC，DA⊥AB，AB=1，CD=4，AD=2，求BC的长.

经思考，学生呈现出如下解题过程：过点B作AD的平行线与线段CD相交于点E，此时BE与DC垂直，由此可确定四边形ADEB为一个矩形，根据矩形性质可知BE=2，CE=3，根据勾股定理可得BC=.

追问1：你是怎样想到这样作辅助线的？

设计意图 这个追问的目的在于让学生说一说辅助线得来的依据，在这个问题的引领下，学生总结出：在直角梯形中构造出矩形，可以获得许多相等的量，将多个条件集中到一起，可以构造出待求线段相关的直角三角形，有了直角三角形就能结合勾股定理获得线段的值.

追问2： 作出的辅助线和梯形中原有的线段存在联系吗？

设计意图 此问的目的在于引导学生从多个维度来思考辅助线的作法，所作辅助线可从梯形的高出发，也可从AD的平行线或平移AD的角度来思考. 多视角思考与分析辅助线，不仅丰富了学生的学习经验，还为解题方法的析离奠定基础.

方法总结：追问的应用，让学生发现作辅助线是解决此类问题的关键切入口，辅助线的目的在于集中分散的三边，至于从什么视角（高、平行或平移）来作辅助线，可根据实际情况来决定. 在追问下，学生获得解决这一类问题的经验——择取恰当的点与方法作辅助线.

历经尝试，验证经验

当学生获得一定的解题经验后，往往会有种跃跃欲试的兴奋感，教师可趁热打铁，结合学情与教情设置难度与梯度恰当的问题，让学生尝试自主应用这些经验，以更进一步强化与巩固学习经验，增强学习信心，提升学习能力. 值得注意的是学生在原有认知经验和新问题之间必须有跨度，又有一定的联系，切忌出现一步到位的问题，要让学生拥有经验迁移的机会.

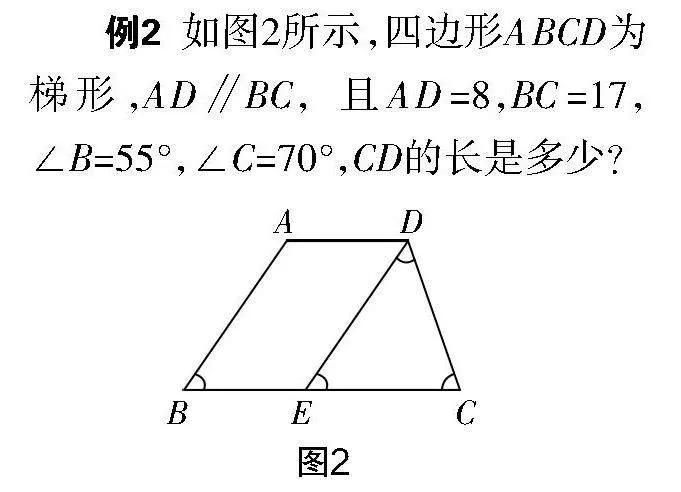
例2 如图2所示，四边形ABCD为梯形，AD∥BC，且AD=8，BC=17，∠B=55°，∠C=70°，CD的长是多少？

学生提出如下解题方法：过点D作DE与AB平行与BC边相交于点E. 根据DE∥AB的条件可知AD=BE，∠CED=55°. 根据∠C=70°的条件，可知∠CDE=55°，由此可推导出EC=DC. 因为AD=8，BC=17，可确定DC=9.

本题与例1有一定关联，解题的关键也是作辅助线，但本题通过矩形的构造解决问题显然不行，但从本题所给定角的度数出发，易联想到作平行线构造角的方法，过点D作DE与AB平行与BC边相交于点E后就构造出一个平行四边形，那么AD=BE则自然生成;从∠C=70°的条件，易联想到∠CDE=55°，问题随之解决.

从本题作辅助线的方法来看，除了构造出平行四边形之外，还与例1相似，将尽量多的条件集中到了一个三角形里面. 借助已有的教学经验，在解决完本题后，同样要求学生说说解决问题的切入点与所作辅助线和梯形原有线段之间的关系. 学生在表述的过程中发散思维，认为既可以理解为作AB边的平行线，也可以理解为平移AB边获得结论.

例3 如图3所示，已知梯形ABCD中的AD平行于BC，AC与BD垂直于点O，AD，BD，BC的长度分别为3，12，10，求AC的长度.

过点A作AE∥DB，与CB的延长线相交于点E. 此时可获得以下结论：∠EAC=90°，AD=EB，AE=BD，由此可推导出CE=BE+BC=13，根据勾股定理可得AC的长. 同理，过点D作AC的平行线DF，与BC的延长线相交于点F，获得BD的长.

本题与前两题相比发生了一些变化，前两题的辅助线都位于梯形内部，而本题的辅助线却处于梯形外部，这与学生已有的认知经验形成矛盾. 认知冲突的形成为进一步发展思维奠定了基础，此处需引导学生分析“本题与前两题相比，哪里不一样？解题关键是什么？有什么收获等”.

学生将初步形成的认知经验应用到实际问题中，不仅进一步夯实了知识基础，还获得了解题技巧，验证了经验的可靠性.

总结提炼，提升经验

解决梯形相关问题的关键在于作辅助线，学生一旦经历且积累了丰富的经验，形成独特的解题技巧后，教师可带领学生对经验进行概括性总结，帮助学生形成触类旁通的解题能力. 鉴于这些经验是零散、无条理的，教师可带领学生将这些零散的经验进行概括与提炼，形成有序思维.

提炼过程如下：①带领学生思考每一种情况下所作辅助线的共同点，将辅助线与原有线段建立关联;②从平移的视角来观察梯形固有线段，分析其平移后的状况;③观察隐含的线段，如梯形的对角线、高、角平分线等是否可以平移，平移之后会发生什么情况？④思考梯形中的线段除了可以进行平移处理之外，能否延长、缩短等;⑤思考线段之外条件的变化，如角的变大或缩小等;⑥熔炼上述思考;⑦甄别已经遇到的问题，探索辅助线的几类作法，为后续解题建立路径次序;⑧遇到复杂的梯形类问题，主动应用如上策略进行验证，丰富自身的解题经验;⑨灵活应用所获得的解题经验，形成解题能力.

以上步骤的实施需结合具体问题而定，并非要求完全按部就班地应用在解决某一类问题中，可根据学生的实际认知经验进行循序渐进的逐步渗透，让学生通过对一类问题的研究，总结提炼解题路径与方法，再将这些方法迁移到另一类问题的解决中去，形成良好的循环.

从本节课梯形问题的研究来看，解决几何问题需依托对基本元素的变换，如线段的平移旋转或角度的变化等，再结合严谨的推理形成结论. 结合已知条件与待求结论，通过对线或角等基本元素的变化就能突破一些解题障碍，尤其是恰当的辅助线是解决复杂几何问题的重中之重.

总之，想要从真正意义上突破“遇到做过的题目就会，遇到没做过的题目就懵”的状态，就需从解题经验的培养着手，让学生在经验的形成、验证与提升中获得举一反三的能力.