基于旧知引出新

作者简介：陈秀娟（1977—），本科学历，中学一级教师，从事初中数学教学与研究工作.

[摘 要] 基于一次函数视角看二元一次方程（组）、一元一次方程、一元一次不等式是函数教学的重点和难点. 教学时教师可利用PPT将系列问题渐次呈现，通过对话、追问，引导学生从旧知过渡到新知，并学会自主归纳、概括新知. 此外，教师要特别重视数形结合思想的渗透，可以安排不同的学生上台，结合图形演示讲解，以便诊评学生对数形结合的理解和掌握情况.

[关键词] 一次函数;一元一次方程;一元一次不等式;数形结合

写在前面

苏科版教材把“一次函数”安排在八年级上册，而且是先安排一个课时单独学习一次函数与二元一次方程之间的关系，后续课时才学习“一次函数、一元一次方程和一元一次不等式”（本文简称“三个一次”）， 所以教师教学“三个一次”时，要充分考虑学生的“最近发展区”，要尽量从上一课已学内容出发，设计开课情境问题，然后引出本课要研究的内容.

“三个一次”新授课教学设计

教学环节1：复习旧知，引出新知

问题1：如图1所示，在平面直角坐标系中，直线y=-x+3与x轴、y轴分别交于A，B两点.

（1）自主设计一个问题，并在小组内说说你的设计意图;

（2）画出正比例函数y=2x的图象，设其与直线y=-x+3交于点P，求点P的坐标;

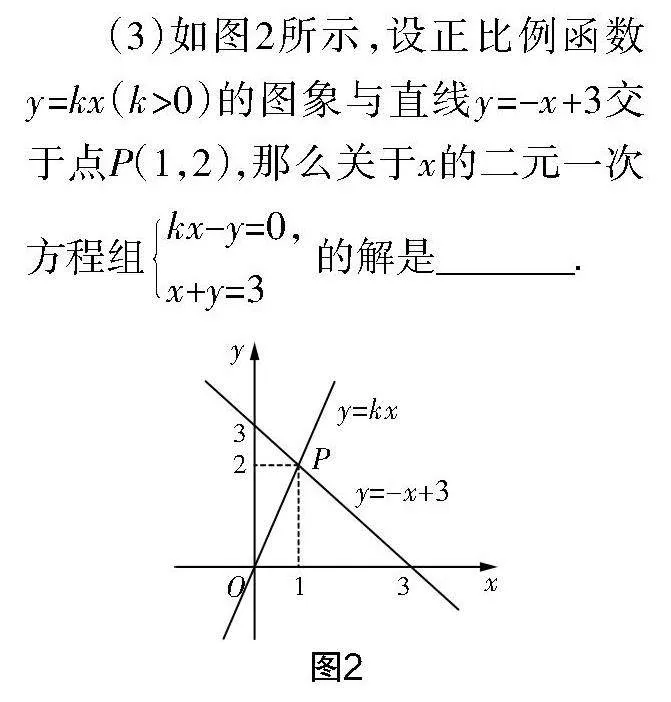
（3）如图2所示，设正比例函数y=kx（k>0）的图象与直线y=-x+3交于点P（1，2），那么关于x的二元一次方程组kx-y=0，

x+y=3 的解是_______.

教学预设：“问题1”的各个小问以PPT形式渐次呈现. 实际教学时，教师还可以让学生先画出直线y=-x+3，再画一个正比例函数的图象，然后提出一个与一次函数有关的数学问题，并在小组内交流. 这个环节主要是让学生复习旧知，因为旧知中蕴含着即将要重点学习的内容. 特别地，如果学生提到了一次函数图象与坐标轴的交点，那么就为后续研究一元一次方程提供了引出情境.

这一环节，学生应该会想到很多问题. 当然，如果学生没有想到一次函数与二元一次方程（组）相联系的问题，教师可出示PPT展示一个相关问题.

教学环节2：探究新知，归纳概括

问题2：以一次函数y=-x+3为例，刚刚有同学研究了该函数的图象与x轴公共点的问题，那如果不画图，能否心算出这个公共点的坐标？你是怎么算的？

教学预设：研究完这个特例问题后，教师可安排学生继续思考一次函数y=2x+4的图象与x轴公共点的横坐标与方程2x+4=0的解之间的对应关系，进而推广到研究一次函数y=kx+b与一元一次方程kx+b=0的关系. 最后，让学生小结出一次函数图象与x轴交点的横坐标与对应一元一次方程的解之间的一般规律.

小结之后，教师可安排教材上一道体现一次函数与一元一次方程的例、习题，从而体现以课本为主线推进学程：一根弹簧的长度为y，所挂物体的质量为x，y与x之间的函数图象如图3所示，则当y=35时，该弹簧所挂物体的质量是多少？

教学环节3：继续探究，成果扩大

问题3：继续研究直线y=2x+4，根据图象，你能否直接说出不等式2x+4>0，2x+4<0的解集？

教学预设：安排学生结合图4，以方程2x+4=0的解x=-2为基础，得到结论“当x>-2时，y>0，即不等式2x+4>0的解集为x>-2;反之，2x+4<0的解集为x<-2”.

拓展追问1：从函数图象的视角分析不等式2x+4≥6的解集.

拓展追问2：从函数图象的视角分析不等式组-2≤2x+4≤6的解集.

教学预设：让不同的学生结合图5，数形结合地演示讲解他们的理解. 如果课堂教学时间允许，教师还可以安排学生自主列举一些不等式，画出相应函数的图象，数形结合地演示不等式的解集.

教学环节4：课堂小结，布置作业

小结问题1：本课学习了从一次函数视角看一元一次方程，可举例说说你是如何理解的吗？

小结问题2：从函数图象的角度分析一元一次不等式x-3>1的解集.

小结问题3：从函数图象的角度分析方程x-3=1-x的解，以及不等式x-3>1-x的解集.

设计意图 “小结问题1”主要是从知识层面组织学生进行回顾，学生可以通过举例说出自己的理解;随后两个小结问题则明确要求学生结合具体的例子数形结合地分析、理解，以反馈学生对本课所学内容的掌握情况. 也就是说，小结问题的设计针对具体课型应有所区别. 比如有些新授课知识点多、概念也多，此时可以侧重于知识、概念的回顾与梳理，而像本课这样突出数形结合眼光、分析策略的，重在实际操作与解题运用，此时小结问题可以相机地运用具体习题来反馈学情.

教学立意的进一步阐释

1. 遵循教材顺序，基于旧知引出新知

教材编写组都是由数学家、数学教育家、数学教研专家、数学专家教师等组成的，对于教材内容的编排顺序是反复考量、精心设计的. 一般情况下，一线教师在没有深刻理解的情况下，不宜本着所谓“学材重组”的理念变动教材顺序，而应尽量遵循教材顺序，想清教学出发点、学情生长点，基于旧知引出新知.

2. 预设对话追问，引导学生概括新知

教师在备课时，除了要研究教材、精心选题而外，还要重视各个教学环节中问题的呈现方式. 笔者以为，教师首先要加强对话追问的过渡语的预设. 比如，不必急于呈现一个问题的全貌（有些习题单式导学案常有类似现象），可以使用PPT出示一个问题的题干，让学生理解、读懂题干之后，再安排学生想想能提出怎样的问题. 如果学生能想出贴近本课的问题，教师可顺势引出本课要研究的问题，这样的对话追问就起到了很好的问题过渡作用. 另外，教师要重视启发式教学，要引导学生概括新知. 比如，对于一次函数与一元一次方程之间的关系，教师要让学生从图象中观察一次函数图象与x轴交点横坐标与相应的一元一次方程的根之间的对应关系，然后让学生变式举例，从不同的角度发现规律，进一步引导学生归纳、概括规律，最后走向一般，概括本课所学的新知. 如果学生概括的语句不够完整或有缺陷，教师可组织活动进一步完善或修正，体现新知生成的“曲折”——数学概念的生成常常有“由粗糙到精致”的过程.

3. 重视数形结合，促进学生感悟方法

从函数观点看方程、不等式的教学关键就是训练学生利用数形结合解题的能力. 史宁中教授在一些报告中反复说过“数学是‘看’出来的”，大概也包含这样的思想. 以本文关注的课例来说，教师要重视学生利用数形结合思想分析问题的能力的培养. 比如，在复习旧知环节，让学生对照两个一次函数图象的交点，说出对应的二元一次方程组的解;在引出新知环节，让学生指着图象，辨别一次函数图象（直线）与x轴公共点的横坐标，并指出对应的一元一次方程的解;在变式拓展环节，让学生画图分析一次函数的函数值的取值范围与对应的一次不等式的解集之间的关系.