借助数学实验 促进深度学习

作者简介：严剑调（1994—），本科学历，中学二级教师，从事初中数学教学与研究工作.

[摘 要] 数学实验是促进深度学习的“催化剂”.本文以“三角尺拼角”的实验教学设计为例，具体从“操作思维是践行深度学习的基础”“合作探究是践行深度学习的关键”“过程结果统一是践行深度学习的核心”三方面谈一些思考.

[关键词] 数学实验;深度学习;拼角

数学实验在数学研究中并非占有主体地位，因为数学结论本身就具备确定性，课堂中不需要大量实验进行验证. 但从教学的角度出发，将数学实验与深度学习有机地融合在一起，能发挥出实验独特的教育价值. 研究发现，若将动手操作与信息技术相结合进行数学实验，往往能有效促进深度学习的发生.

实验设计

活动1 要求学生用一副三角尺进行拼角，同时思考以下几个问题：①大家观察手中的三角板，说说拼成的角度;②观察拼角，可获得什么结论？③以上观察都是从“形”出发，若从“数”的角度思考，能获得哪些角度？

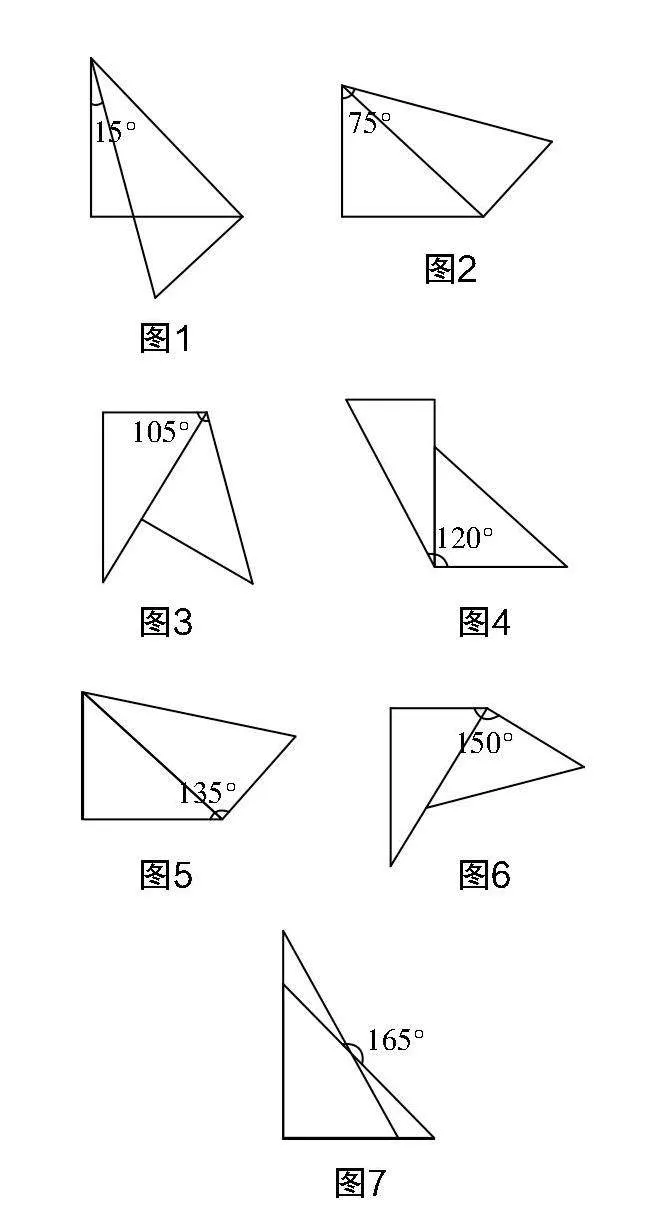
借助多媒体展示学生的拼图，如图1～图7所示.

设计意图 从手动操作出发，学生通过层次清晰的活动产生探索欲. 学生观察拼角，讨论结论的过程，需通过小组合作学习的方式来完成，这是提升学生协作能力，促进深度学习的基础. 第三个问题要求学生从“数”的角度思考拼角问题，希望学生通过动手、动脑对实验进行观察、猜想、总结等，以提升理性认识，促进深度学习的发生.

活动2 用两副三角板拼角，同时思考以下几个问题：①两副三角板可以拼出哪些角？小组讨论并介绍拼法;②能否拼出所有15°整倍数的角？③如果用更多三角板，能否拼出其他度数的角呢？

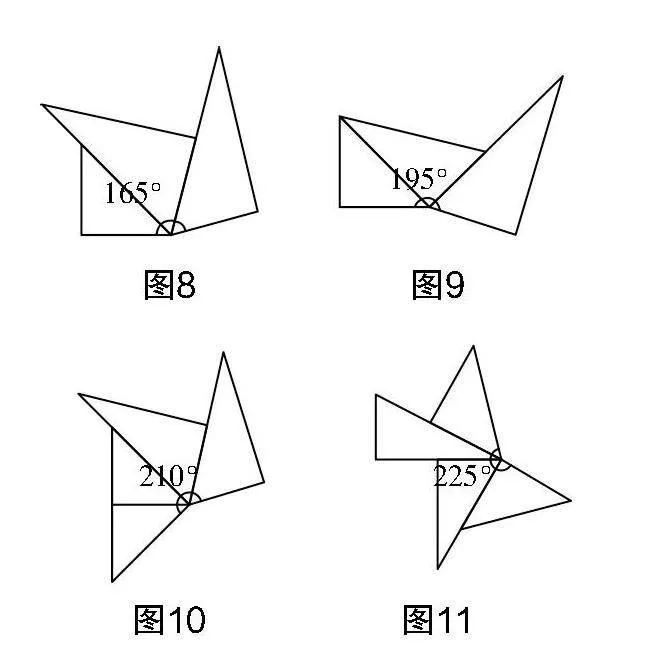
如图8～图11所示，借助多媒体展示部分学生用两副三角板所拼成的图形.

设计意图 活动2进一步深化了学生对三角板拼角的认识，学生的思维从感性转化到理解阶层. 此活动设计意在训练学生的观察与分析能力，让学生的思维从直观形象转化到抽象逻辑. 可视化的操作到抽象的数据分析，进一步提升了学生的深度学习能力，学生从中感悟到实验背后所蕴含的方法与原理等，为后续利用模板拼角奠定了基础.

活动3 设计实验模板，思考以下几个问题：①若有17°与19°的模板，尝试借助铅笔与模板分别画1°与2°的角，思考还能拼出哪些度数的角;②用17°与19°的模板是否可以拼出所有整度数的角？③尝试自己设计模板进行拼角;④若设计出来的模板为a°与b°（a，b均为整数），可以画出哪些角？

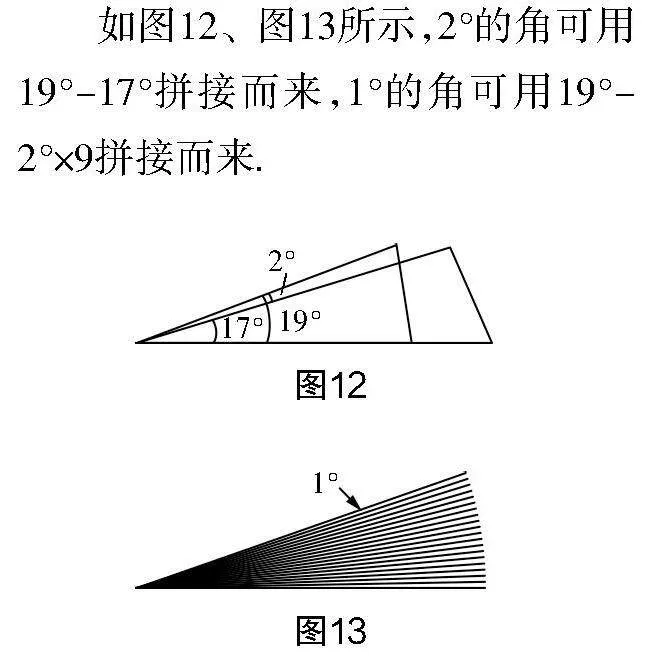
如图12、图13所示，2°的角可用19°-17°拼接而来，1°的角可用19°-2°×9拼接而来.

设计意图 学生根据教师所提供的模板自主计算拼接出1°和2°的角，由此可确定任意整数度数的角都可以拼出来. 该实验的目的意在让学生经历从特殊到一般的过程，让学生发散思维，获得归纳推理能力，从真正意义上践行深度学习理念.

教学思考

1. 操作思维是践行深度学习的基础

传统教学，教师更关注知识基础的教学，要求学生掌握知识的结论，并利用所得结论解决实际问题，而对于学生动手操作能力的培养鲜少关注. 殊不知，数学理论的获得往往来自实际操作. 想要践行深度学习理念，首先就要拥有良好的数学操作思想，因为从真正意义上掌握教学内容绝非依靠单纯的记忆或模仿，而应通过在实际操作的基础上获得直观感知，让学生对知识的认识实现从感性到理性的转变，这也是学生获取数学知识，形成良好应用能力的关键.

本节课，教师带领学生从三角板拼角出发，让学生通过自主操作来直观感知拼角情况，进而启发学生的操作思维，让学生初步形成结论. 在此基础上，提出用模板拼角的问题，使得学生再次通过操作进一步认识拼角过程与特点. 这种逐层递进的实验操作方式，使得学生从真正意义上体会到知识的形成与发展需经历怎样的一个流程，这对促进学生数学思维的发展具有重要意义，深度学习则在此操作中发生.

2. 合作探究是践行深度学习的关键

数学实验操作从本质上来看，属于一种探究性活动，需要依靠学生的合作来完成一些任务. 学生边操作、边思考教师所提出的各个问题，在观察与分析中探索知识特点. 因此，数学实验一般会选择具有开放性、挑战性的主题，学生在富有探索价值的问题中操作，感知新课标所提倡的“自主探究、实践操作与合作交流”相结合学习模式，并从中体验团队的力量，这是践行深度学习理念的关键.

本节课的模板设计环节，教师鼓励学生以小组合作学习的方式进行探讨、交流、设计，并与学生积极互动，一起探索设计模板的方法，耐心倾听学生的意见. 巡视过程中，笔者发现其中有一个小组设计出3°，5°以及8°的模板，模板设计没有问题，但在思考这几个模板可以拼接成怎样的角度时出现了障碍.

为了顺利解决这个障碍，教师鼓励学生利用模板进行拼角. 操作中，学生自主发现可以获得所有1°整倍数的角，大家因为得到这个结论而兴奋，不知不觉中就达到深度学习的目的. 由此可以看出，在良好的情境中学习，学生在实验操作与合作交流可不断提升自身的认知水平，形成合作共同体，促进教学相长.

教师作为数学实验的组织者与活动探索的引领者，应站到学生的角度来分析与思考问题，引导学生学会用数学的眼光、思维与语言来看待、思考与表达对这个世界的情感，让学生在合作探究中取长补短、协同共进，感受数学学科独有的魅力.

3. 过程结果统一是践行深度学习的核心

在以中考为背景的情况下，不少教师为了提高升学率，过于追求学生对知识结果的掌握程度，片面地认为学生只要掌握了相关的结论，就能应用这些结论去解决问题. 事实上，数学结论的形成需要经历一个过程，学生只有亲历其形成与发展过程，才能从真正意义上实现深度学习，这是培养与发展学生数学核心素养的关键一步.

斯托利亚认为：数学教学不仅仅是结论的教学，而是数学活动、思维的教学. 事实告诉我们，将数学过程与结果统一起来，才能促进学生形成终身可持续性发展的学习能力. 数学实验就是将抽象的结论转化为直观可视的一种方式，即通过实验操作探寻数学结论，让学生在探索过程中发现知识背后隐藏的数学思想方法等，从而更加深刻地理解并掌握结论，为灵活应用夯实基础.