基于PC-CFB的磨煤机分离器产品细度数值模拟

尚曼霞，姚禹歌，柯希玮，周托，黄中

(清华大学 热科学与动力工程教育部重点实验室，北京，100084)

为助力“双碳”目标的实现，我国提出要构建适应新能源占比逐渐提高的新型电力系统[1]，然而新能源发电的不稳定性和随机性将会对电力系统的安全构成巨大冲击。因此，煤电的定位将由电量型向调节型转变，以保证电网的安全。循环流化床实现了劣质煤的高效清洁利用，在中国的煤电装机容量中占比约为10%，也是未来参与电网深度调峰的主力。然而，循环流化床锅炉在负荷调节速率、深度低负荷及低负荷下的NOx排放控制、受热面磨损等方面，还有较大的改善空间[2-3]。研究和工业验证表明[4-5]，降低循环流化床锅炉给煤粒度能够提高锅炉负荷调节速率、降低NOx的原始排放等，改善锅炉运行特性。基于前人的研究成果及课题组多年的探索积累，本文提出了粉煤循环流化床(powdered coal-circulating fluidized bed, PCCFB)燃烧技术[6]，通过将流化床给煤粒度由传统的0～10 mm 宽筛分分布降低为0～1 mm 的窄筛分分布，降低床料粒度，提高床质量[7]；通过流态调控化学反应，强化低氮燃烧需要的还原性气氛，并为延长细颗粒石灰石在炉内的停留时间提供了保证，同时燃料颗粒的反应表面积得到提高，有利于燃烧性能的改善。

制粉是实现PC-CFB技术的核心，采用中速磨煤机实现粉煤的制备。其中，磨煤机顶部分离器是决定产品细度的关键，学者们对其开展了众多的数值及实验研究。苟琮琦等[8]对某电厂ZGM95G型中速磨煤机进行了分离器转速特性试验、磨煤机通风量试验等，经过试验优化得出了新的磨煤机出力与分离器转速及磨煤机风量对应等曲线，改善了磨煤机煤粉细度；李红[9]利用按4∶1 比例缩小的实验室煤粉分离器，开展了变风量的煤粉分离试验，发现综合分离效率在中间风量(150 m3/h)时，达到最大值(约为40%)，并随着风量的增大而保持平稳。由于工业型磨煤机占地大，实验操作较为困难且成本高，因此许多学者利用数值模拟手段开展了相关研究。VUTHALURU 等[10]利用Euler-Euler 方法对磨煤机内部的气固两相流动进行了计算，获得了流场及颗粒运动轨迹；吕太等[11]采用离散相模型(discrete phase model, DPM)和RNG 模型(re-normalization group model)对不同挡板开度下分离器内部气体流场和颗粒运动进行模拟，发现分离器挡板开度越小，分离效果越好，但同时内部阻力也会增大，最终确定了最佳挡板开度区间；LIU等[12]采用DPM和RNG模型对磨煤机的流场特性进行了计算，并探讨了挡板形状、数量等参数对流场和分离器分离效率的影响，优化了挡板设计。

但前人研究中的产品粒度均为0～200 μm 的常规产品粒度范围，不满足PC-CFB 技术的制粉要求，且采用的计算模型未考虑颗粒对流体的作用以及颗粒间的相互作用。为此，本文作者以一台工业型磨煤机为对象，应用计算精度更高的稠密离散相模型(dense discrete phase model, DDPM)和颗粒流动力学理论(kinetic theory of granular flow,KTGF)的四向耦合方法，对拆除挡板后的工业型磨煤机分离器内部的气固流动进行数值研究，以期提高产品煤粉细度，满足PC-CFB技术对入炉煤粒度的要求。

1 磨煤机分离器数值计算方法

1.1 几何模型及网格划分

研究对象为ZGM80 型磨煤机分离器，其几何模型如图1所示。

图1 磨煤机分离器几何模型Fig. 1 Geometric model of vertical spindle mill separator

采用ICEM CFD 软件对模型进行结构化六面体网格划分，取Y=1.2 m 截面与X=1.5 m 截面交界线上的切向速度进行网格无关性验证，如图2(a)所示。由图2(b)可知：当网格数从54万个变为196万个时，切向速度变化范围在5%以内，考虑到计算成本，最终选取的网格数为54 万个。网格划分情况如图2(c)所示。

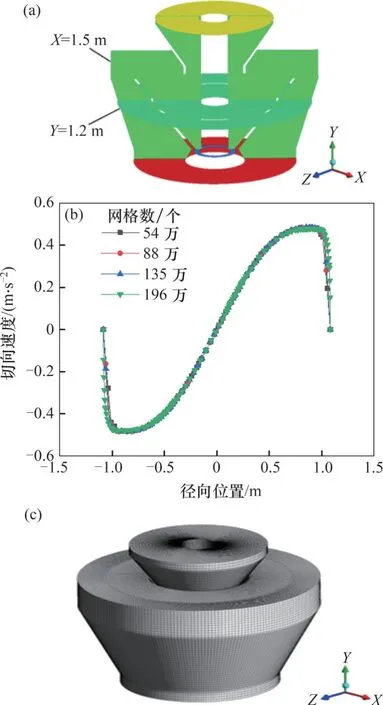
图2 磨煤机分离器网格Fig. 2 Grids of vertical spindle mill separator

1.2 数学模型

煤粉由气流携带自下向上进入分离器内部，粗颗粒煤粉在离心力的作用下被甩到分离器壁面附近，并在重力作用下返回到磨机内部继续研磨；细颗粒煤粉则由气流携带经分离器顶部出口作为产品排出。分离器内部的流动为带有旋流的湍流，对这类流动描述较为准确的有大涡模拟(large eddy simulation, LES)、雷诺应力模型(reynolds stress model, RSM)等，考虑到计算成本及时间，采用RSM模型[13-14]。

对煤粉颗粒的追踪采用DDPM 模型计算。该方法考虑了颗粒对流体的作用以及颗粒间的相互作用，引入“parcel”的概念将颗粒“打包”计算，并将颗粒相群体的特性映射到欧拉网格计算连续颗粒应力场，在计算精度和计算成本上都具有较强的优势[15-18]。

1.2.1 气相控制方程

磨煤机分离器内的气体流动可视为等温流动，气相的质量和动量守恒方程如下。

质量守恒方程：

动量守恒方程：

式中：εg为气相体积分数；ρg为气相密度，kg/m3；vg为气相速度，m/s；p为混合相压力，Pa；τg为气相的应力张量；g为重力加速度，m/s2；Kgp为每个网格单元从固相到气相的界面动量交换系数；vp为颗粒速度，m/s。

1.2.2 颗粒相控制方程

DDPM 模型中，颗粒相在拉格朗日参考系中进行描述，采用牛顿第二定律描述颗粒运动[19]：

式中：ρp为颗粒密度，kg/m3；表示重力引起的颗粒加速度，m/s2；表示由压力梯度力引起的颗粒加速度，m/s2；表示由颗粒间相互作用力引起的颗粒加速度，m/s2；FD(vg-vp)表示由曳力引起的颗粒加速度，m/s2。曳力FD采用Gidaspow模型进行计算[17]：

式中：CD为曳力系数；εP为固相体积分数；dp为颗粒直径，m；μg为气相动力黏度，Pa·s。

颗粒应力张量σp表示基于欧拉网格计算的颗粒间相互作用，采用下式进行计算[18]：

式中：pp为固相压力，Pa；为单位张量；μP和λP分别为固相动力黏度和体积黏度，Pa·s，具体计算方法参考文献[20-21]。

1.3 边界条件

图1中，磨煤机分离器底部红色圆环区域为气体和颗粒的入口，将其设为速度入口边界；磨煤机在正常工作条件下，分离器内部为200 ℃左右的高温状态，故将气体设定为200 ℃的空气，速度为5.6 m/s；颗粒入射速度与气体一致，密度设为1 300 kg/m3，入口粒度分布如图3所示；分离器顶部黄色圆环区域为产品出口，底部蓝色圆环区域为返料出口。将入口与产品出口设置为完全逃逸边界，返料出口设置为捕捉边界，壁面设置为反射边界。采用瞬态计算，经过调整，时间步长设置为0.001 s。

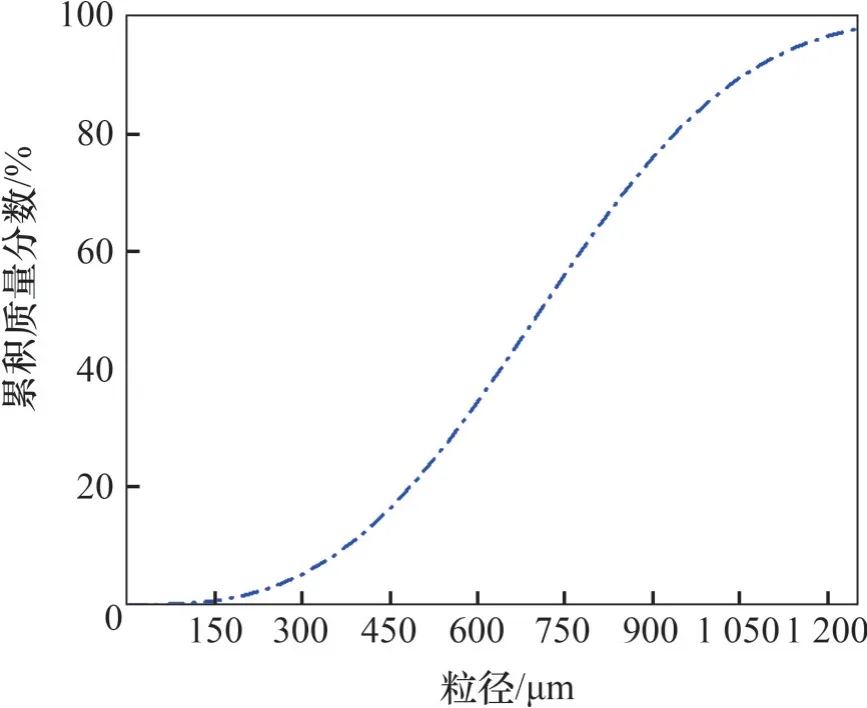
图3 入口粒度分布Fig. 3 Particle size distribution at inlet

2 结果与讨论

计算前，对模型进行了验证，验证结果如图4所示，模型计算所得的煤粉产率与实验结果间的偏差在5%以内，且产品粒度分布与实验测量结果相近，平均偏差在10%以内，证明所选模型具有较高的精确度，因此，采用模型对磨煤机分离器内的气固流动进行计算。

图4 模型计算结果与实验数据[9]的比较Fig. 4 Comparison of calculation results with experimental data[9]

2.1 磨煤机分离器内部流场

选取Z=0 m 的截面查看流场的速度矢量分布，分析磨煤机分离器内部的流场特性。图5(a)、(b)、(c)所示分别为气体的轴向、径向和切向速度矢量分布，三者均呈现明显的对称分布。相较于轴向速度，径向速度与切向速度分布均匀，其中径向速度在分离器内外锥体相接区域与下部返料出口区域数值明显增大，这是由于气体在流经该处区域时截面变窄，最终被加速；由于缺少了挡板的导流作用，气体进入分离器内锥体区后产生的旋转流动被削弱，切向速度较小，其低于8 m/s 时，有利于粗颗粒的排出，提高产品细度。

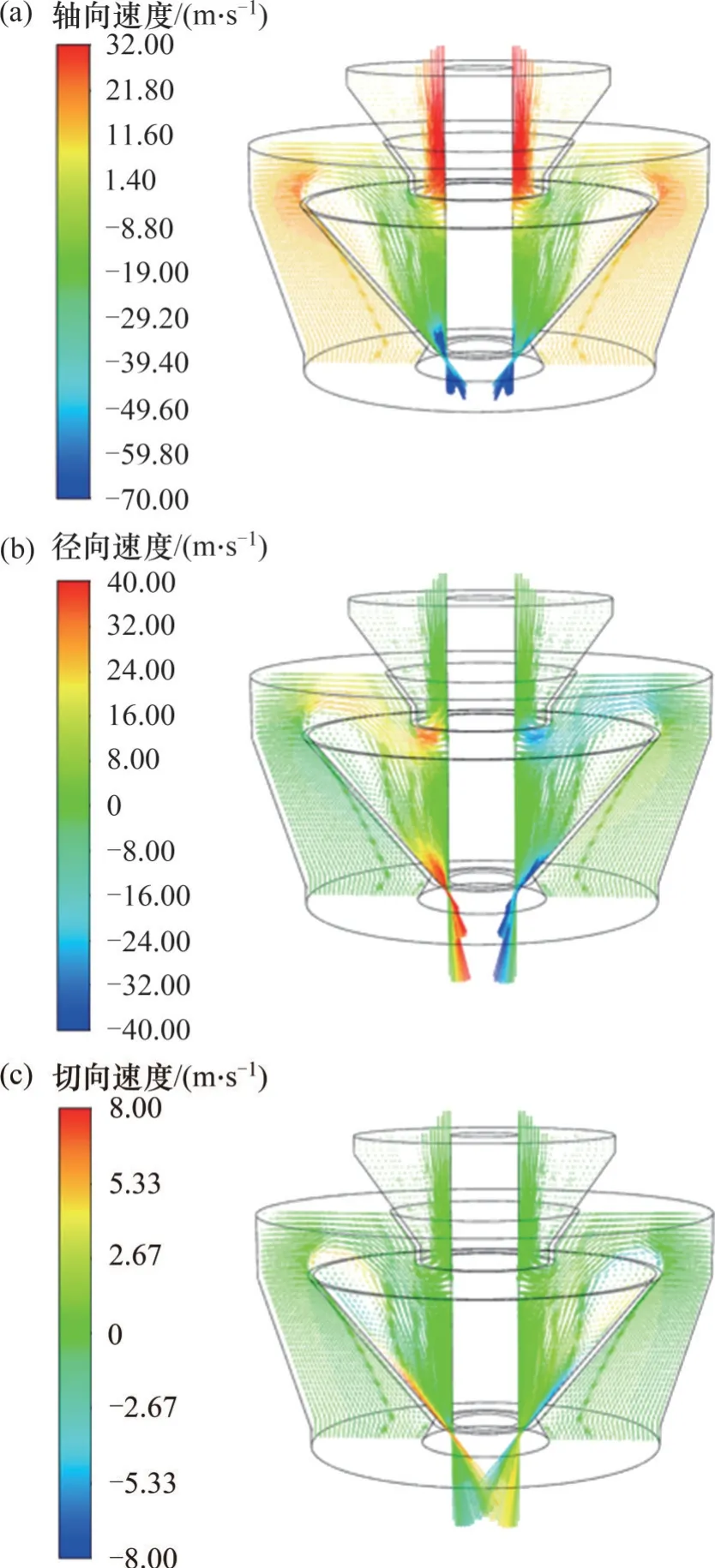
图5 磨煤机分离器Z=0 m截面速度矢量分布Fig. 5 Velocity vector distributions in Z=0 m section of vertical spindle mill separator

图6 分离器不同区域轴向速度分布Fig. 6 Axial velocity distributions in different areas of separator

分离器内不同区域轴向速度分布差别较大，因此，选取Z=0 m与Y=0.40、0.60、1.40和1.95 m 4个具有代表性截面的交界线提取数据进行作图。经过分离器入口时气体流速较低，由于通过的区域截面不断变窄，气体被加速，内、外锥体相接区域处，气速可达15 m/s。由于构造原因，靠近内边壁区域的气速大于外边壁区域的气速，约为5 m/s；通过分离器内、外锥体相接的区域后，气体分为两路，一路沿顶部产品出口流出，且速度相近；一路转而向下沿底部返料出口流出，且由于内锥体的构造，区域截面不断收窄，气体速度沿Y轴负向不断增大，最高可达70 m/s。

2.2 磨煤机分离器内部颗粒运动

在流场的基础上，加入颗粒进行计算。在进行分析之前，首先应该保证模拟中，系统已经达到稳定状态。系统随时间的稳定性分析主要通过监测分离器产品出口和返料出口的颗粒质量流率来确定。2个出口的颗粒质量流率随时间的变化情况如图7所示。由图7可知：在初始阶段，由于颗粒需要一定的时间运动到出口，2个出口的颗粒质量流率为0 kg/s；t=0.6 s，出口开始监测到颗粒；2个出口的颗粒质量流率稳定增长，t=5.0 s时，产品与返料质量流率趋于稳定，分别约为10.6 kg/s 和38.9 kg/s。因此，可以判定，当t=5.0 s，分离器系统已达到较为稳定的状态。

图7 分离器出口颗粒质量流率曲线Fig. 7 Particle mass flow rate curves at separator outlet

图8所示为不同时刻分离器内部颗粒的粒度分布情况。颗粒从外锥体区底部进入，在上升气流的作用下向上运动，并通过内、外锥体相接的区域，进入到内锥体区，随后一部分颗粒上升至产品出口，一部分颗粒下落至返料出口。由图8(a)可以看出：最细的颗粒从分离器底部运动到内、外锥体相接的区域所需的时间约为0.3 s，粗颗粒仍分布在外锥体区域。另外，颗粒在外锥体区运动过程中，已经呈现明显的分层现象，细颗粒上升速度明显比粗颗粒的快。从图8(b)可见：t=0.6 s时，大部分细颗粒进入内锥体区域，且已经运动至底部返料出口。从图8(c)可见：t=1.0 s时，在入口颗粒的持续注入下，分离器内部颗粒数量明显增多，且颗粒在分离器中的粒度分层现象更加显著，细颗粒主要分布在分离器顶部区域；从图8(d)可见：t=5.0 s 时，分离器内部颗粒流动达到稳定，产品出口、返料出口均有颗粒连续稳定排出，且细颗粒集中分布在内锥体区域。

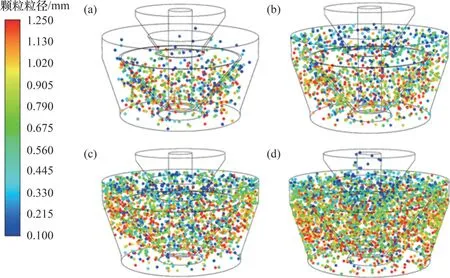
图8 不同时刻分离器内颗粒粒度分布Fig. 8 Particle size distributions in separator at different time

通过以上分析，当t=5.0 s 时，整个分离器已经处于稳定的工作状态。因此，选取t=5.0 s 后的某一时刻，即t=6.0 s，分析颗粒的粒度分布。图9所示为Z=0 m 与Y=0.40、0.60、1.40 和1.95 m 截面的颗粒粒度分布云图。图8(a)中，颗粒呈现明显的分级现象，尤其在内锥体区，大量的粗颗粒在离心力、曳力和重力的共同作用下，沿着边壁下落到返料出口；细颗粒则进入分离器顶部沿产品出口流出。由图9(b)～(e)可知：颗粒沿截面半径分级的情况较为明显，细颗粒多分布在内壁区域，而粗颗粒多分布在外壁区域。

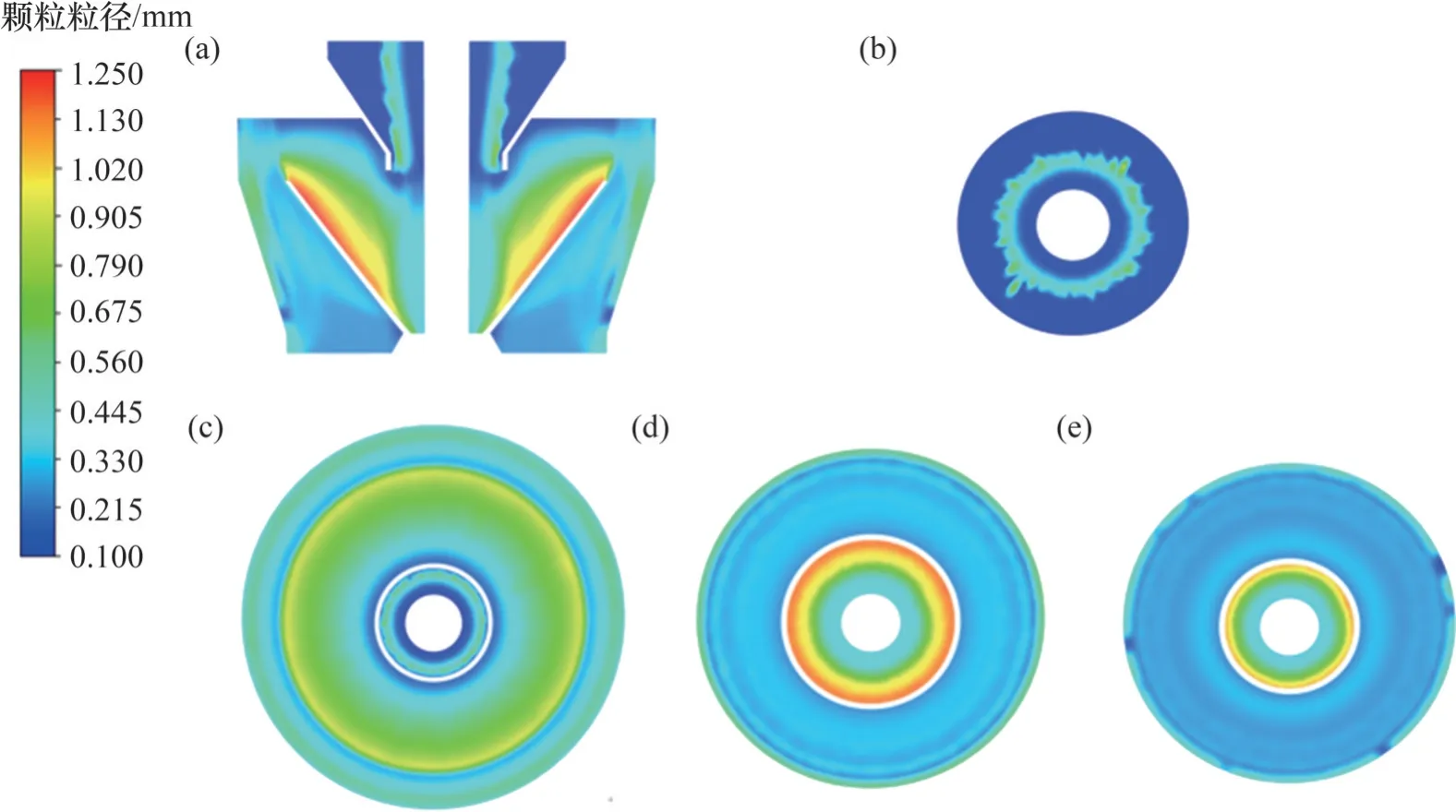
图9 颗粒粒度分布云图(t=6.0 s)Fig. 9 Contours of particle size distribution(t=6.0 s)

对t=6.0 s 时产品出口的颗粒粒度分布进行统计，结果如图10 所示，产品粒度分布符合PCCFB技术的要求。

图10 产品出口粒度分布Fig. 10 Particle size distribution at product outlet

由于拆除了磨煤机分离器顶部挡板，且厂家提供的原有的通风特性曲线为各种规格ZGM型磨煤机的通风特性的归纳，只适用于工程上的粗略估计，因此，需要对不同通风量下分离器的溢流产率进行计算，以获得改造后分离器的通风特性曲线。溢流产率M[9]的计算公式如下：

式中：mo和mf分别为分离器产品出口和入料的质量，kg。

计算所得的不同通风量下的出力如图11所示。采用线性拟合得到分离器的通风量(x)与出力(y)间的关系式为y=2.85x-39.64，决定系数为0.993 78。

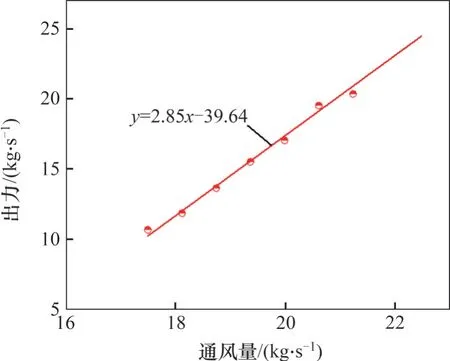
图11 磨煤机分离器通风特性曲线Fig. 11 Ventilation characteristic curve of vertical spindle mill separator

3 结论

1) 为实现PC-CFB技术对入炉煤粒度的要求，将磨煤机分离器顶部的挡板拆除，应用DDPM 模型对ZGM80 型磨煤机分离器内部的气固流动进行了计算。分离器内部径向速度与切向速度分布均匀。由于缺少挡板的导流作用，切向速度被削弱；轴向速度在分离器内部不同区域分布差别较大。

2) 颗粒在分离器内粒度分层现象明显，细颗粒上升速度明显快于粗颗粒上升速度。在气流携带下，返料出口最先有颗粒排出。t=5.0 s时产品与返料2个出口的颗粒质量流率均达到稳定状态，且产品出口粒度分布满足PC-CFB技术对入炉煤粒度的要求，验证了拆除分离器挡板是切实有效的。

3) 对不同通风量下的出力进行了计算，获得了拆除挡板后分离器的通风特性关系式，可应用于工业生产指导。