自由设站法在精密三维控制网构建过程中的应用

王温灵

（上海融测空间测绘有限公司，上海 201803）

随着船舶工业和电子科技不断发展，各种精密设备和传感器在船舶中的应用越来越普遍，对船舶建造中的测量精度要求也越来越高，精准、高效的船舶测量技术越来越受关注。由于测量仪器、方法和技术不断更新，因此需要研究人员不断寻求更优质、更适用的方案。

自由设站测量法常用于各等级控制网的加密、各类工程测量、临时设站或传递坐标测量以及独立工程控制网的建立与加密测量工作中[1]。高铁CPIII 控制网就是采用自由设站法进行观测的，控制网以线性和平面为主要特征[2-3]。自由设站法也经常应用于变形监测中（多为单站式）[4]。该文以某大型测量船为研究对象，探究应用测量精度高、作业灵活且操作简便的自由设站法，在地面高精度首级网的基础上，利用多个已知点、未知点和自由设站点构建环形三维控制网，并分别建立平面和高程平差计算模型的方法。为了提高船舶测量的精度，该文提出新的控制点布设方式和观测方法，通过试验构建一个控制网布设与测量模型，并结合控制网的特点构建平差计算模型，该模型具有较高的通用性，便于编程。

1 研究设计

1.1 研究对象

该大型测量船的总长约125 m，型宽约25 m，罗经甲板与地面高差约25 m。需要精密测量位于船底及甲板层的多台传感器设备的三维空间相对位置（设计精度如下：纵坐标X为±2 mm，横坐标Y为±2 mm，高程H为±5 mm），属于精密工程测量范畴[5]。大船位于船台，底部通视条件差，周边作业空间有限，地面可以布设观测墩的位置较少，各层甲板无法布设固定观测墩，日间现场环境干扰因素较多，并且大气环境条件随时间变化较明显，船体随气温变化会产生形变。

1.2 测量仪器和设备

该文采用激光跟踪仪靶球（SMR）配合LEICA TS60全站仪测量精密边长、水平角和竖直角，以构建三维控制网。LEICA TS60 全站仪具有性能稳定、角度观测精度高（0.5″）和距离观测精度高（0.6 mm+1×10-6×D）（D 为测距长度）以及观测效率高等优点，其ATR 自动照准功能配合蓝牙驱动，可以对目标进行连续多测回自动观测与记录，被广泛应用于高等级控制测量、核电、地铁隧道、高铁、水利电力、建筑工程和变形监测等领域。该文采用的靶球（SMR）是直径为3.81 cm（1.5 inch）的空心靶球，是API 激光跟踪仪配套使用的精密标靶，中心三维精度高于±0.5 μm，稳定性高，适合长时间测量；精密圆棱镜为LEICAGPH1P 棱镜，位置精度为±0.3 mm。采用精密靶球代替圆棱镜，可以有效提高全站仪进行自动观测时的照准和测量精度，还可以提高三角高程测量的精度。

1.3 控制点的布设与测量

平面控制网为两级，高程控制为一级，共布设28 个点位，其中平面首级控制点4 个，采用地面强制对中观测墩，高度以视线高于地面50 cm 为宜，每点安置1 套基座和精密圆棱镜并精确整平。在船舷、船体两侧以及船底等设备安装位置附近布设24 个靶球（SMR）点，将其作为加密控制点，磁性靶座用强力胶固定于船体。各控制点均以棱镜或靶球的中心作为实际控制点点位，这样不仅可以最大限度地减少观测目标重复安置造成的精度损失，而且还便于采用激光跟踪仪进行设备精密安装、定位或姿态测量。

控制网的观测时段选择在大气环境变化较小的夜间，并同步精确测量大气环境数据并输入全站仪。每个测站以全圆方向观测法观测2 个测回，在1 个测回中，对测站上所有要观测的方向进行逐一照准并观测，针对零方向，有起始和闭合2次观测[6]。先观测4 个首级点连接成的平面闭合导线，再进行自由设站观测，每个测站观测首级控制点不少于2 个，相邻测站公共观测点数不少于3 个，并保证每个加密点有不少于3 个测站方向的观测，试验中共观测9 站，控制网模型如图1所示。采用自由设站法进行测量可以避免架设仪器时对中误差的传播和积累，而且无须量取仪器高和觇标高，可以提高三角高程测量精度。此外，可以根据观测点位的分布和现场作业环境灵活选择设站位置，在测量过程中进一步优化控制网。

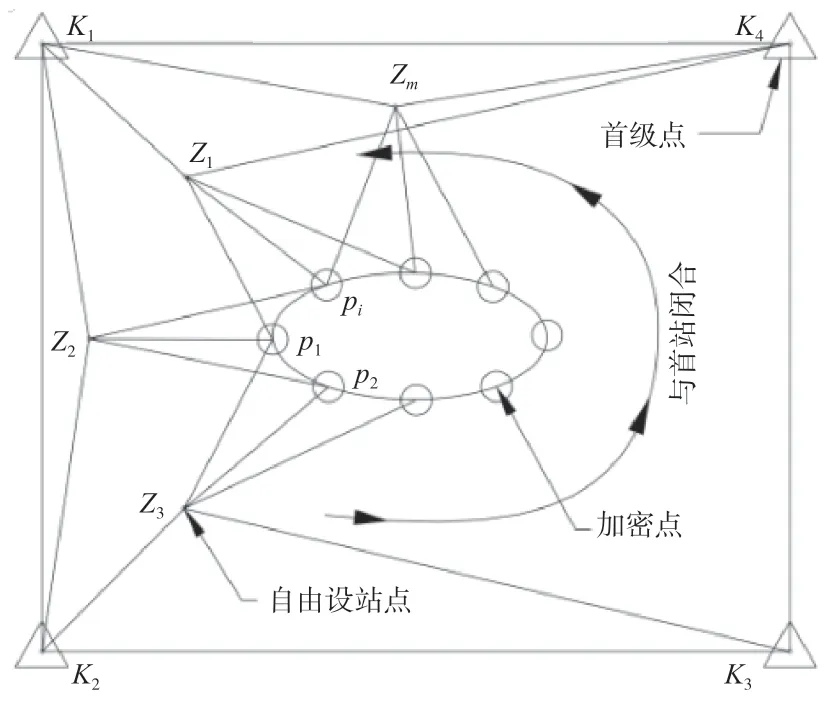
图1 控制网观测示意图

1.4 数据处理模型

控制网的观测数据分包括水平方向角、边长和高差，为了使函数模型具有通用性，采用间接平差法，分别以待定点的坐标和高程为参数建立平面和高程平差模型。

1.4.1 平面控制平差模型

1.4.1.1 函数模型

如图1 所示，首级平面控制为闭合导线K1-K2-K3-K4，以K1点为起算点，K1-K2为起算边。由于首级网的点数较少、观测条件好并采用固定棱镜为目标，因此观测精度容易控制，平差模型简单。

加密网的观测值为水平方向角Bmi和边长Smi，函数模型的建立过程如下：1） 以自由设站点Zm为原点（0，0）建立测站坐标系Om-Xm-Ym，以起始观测方向为坐标纵轴X方向，通过公式（1）计算Zm测站各观测点在测站坐标系下的坐标值（Xpi，Ypi）。2） 将测站内的2 个（或以上）已知点在控制网坐标系（O-X-Y）和Om-Xm-Ym下的坐标对代入二维四参数平面坐标转换模型（如公式（2）所示）[7]，求出4 个转换参数，即Δx、Δy、α和K（测量尺度相同时值取1），再将测站点和加密点的测站坐标代入坐标转换模型，转换为控制网坐标系下的近似坐标（）。根据该参数计算方法建立的模型通用性强，便于编程。3） 列出每个观测方向的坐标方位角的误差方程（如公式（3）所示）和边长的误差方程（如公式（4）所示）[8]。当测站观测方向为已知点时，公式（3）、公式（4）中的，公式（3）、公式（4）分别简化为公式（5）、公式（6）。4） 采用近似坐标反算各观测边的近似方位角、近似边长和各站的定向角（即零方向的方位角）近似值zm0，再结合边长和角度观测值计算误差方程的系数和常数项。

式中：pi为控制点序号；m为自由设站序号（取1，2，…，m）；i为自由设站观测方向序号（取1，2，…，i）；vmi为测站至观测方向的坐标方位角改正数；vi为测站各观测边长的改正数；m为测站定向角改正数；分别为每条边两端点的近似坐标改正数；和均为各边两端点的近似坐标增量；ami、bmi为2 个系数项，；lmi为各边的角度观测值减去其近似值，（jm为m测站上的观测方向数）；li为各边的边长观测值减去其近似值，即。

1.4.1.2 随机模型

随机模型主要确定角度和边长观测值的权比。控制网中角度和边长观测相互独立，随机模型为（σ0为单位权方差；Q为观测向量的协因数阵；P为权阵（对角阵）），网中角度和边长观测数量相同，k1=k2=2m+3i个（k1为角度观测数量；k2为边长观测数量；m为自由设站数；i为自由设站的观测方向数），设总的观测数量k=k1+k2，权阵如公式（7）所示。取测角中误差为单位权中误差，即，那么（σB为测角中误差；σS为测边中误差；PB为角度的权；PS为边长的权）。计算时σB、σS取全站仪的标称精度。

将误差方程（公式（5）、公式（6））转换为矩阵形式，如公式（8）所示。

式中：V为方位角和边长的改正数阵；B为系数阵；l为常数阵；为参数的改正数阵（同时包括方位角和边长的改正数）。

将公式（8）代入公式（9），消去V，有，如公式（10）所示。

1.4.2 高程控制平差模型

1.4.2.1 函数模型

高程控制网观测值为每个观测方向的高差观测值（模型设定K1点为已知点，高程为HK），平差函数模型的建立过程如下：1） 以待求点（包括自由设站点和船体加密控制点）的平差高程为参数，对应点的近似值为H0，改正数为。当推算近似高程时，先计算带有已知点的测站，再计算相邻测站，以此类推，计算所有点的近似高程。2） 网中共观测n=2m+3i（n为高差观测数；m为自由设站数；i为自由设站的观测方向数）条边的高差Lmi，设对应各观测边的高差改正数为vhmi，列出各观测边的观测方程（如公式（11）所示）。当观测方向为已知点时，i=H（ki为 各观测点的平差高程），并入常数项lhmi（如公式（12）所示）。将公式（12）中替换为H0+，整理后得公式（13）。令lhmi=Lmi+Hm0-Hi0（Lmi为各边的高差观测值；Hm0为自由设站点的高程近似值；Hi0为观测方向点的高程近似值），得到误差方程（如公式（14）所示）。3） 根据观测值和高程近似值，计算误差方程常数项。

1.4.2.2 随机模型

因为控制网中各观测高差为同精度独立观测值，所以按照观测边长进行定权Pmi=C/Smi（C为设定的单位权观测边长，试验模型中C=0.2 km），得到观测值的权阵P（P为n行n列的对角阵）。将误差方程转换为矩阵形式（如公式（8）所示），将系数阵B、常数阵l和权阵P带入公式（10），求出参数的改正数阵，即各点近似高程的改正数，再将代入误差方程，计算各边的高差观测值的改正数vhmi。

2 试验结果分析

当进行数据平差时，对比平面控制的2 种平差方式。一种是按照整网平差，即只保留自由设站网，以2 个已知点为起算进行平差。当计算近似坐标时，从带有已知起算点的测站开始，根据上述近似坐标计算方法计算各点的近似坐标，再依次在各测站数据中查找在首站中有3 个以上公共观测点的测站，并以这些公共观测点为重合点计算转换参数，完成这些相邻测站的坐标转换。以此类推，直到完成所有测站的近似坐标计算。另一种是根据首级网和加密网分级平差。地面首级网严密平差结果为方位角闭合差0.4″，坐标闭合差0.7 mm，相对精度为1/330000，最弱点点位中误差0.2 mm。2 种方式的平差结果对比见表1。高程控制按整网平差结果如下：最弱点高程中误差为0.15 mm，最弱测段高差中误差为0.16 mm，根据闭合环统计的测站高差中误差为0.17 mm。

表1 2 种方式平差结果对比

根据试验结果可知，基于自由设站法并使用TS60 全站仪和精密靶球构建的三维控制网在试验模型下的优势如下：1） 观测数据质量稳定，成果精度高，平面和高程平差结果均比设计精度高。2） 平面控制网2 种方式的平差结果均满足设计精度。3） 平面控制按照两级网进行平差后，总体精度更高，点位中误差可以满足一级精密工程控制网的精度要求（相邻点相对点位中误差为0.2 mm）。4） 高程控制网可以达到较高的精度，可以满足四级精密高程控制网的精度要求（测站高差中误差为0.30 mm）。

试验中最弱边和方向测量中误差较大的边主要是部分短边（边长小于10 m），因此，在实际应用中应尽量注意避免出现超短边，以获取更可靠、精度更高的观测数据。模型中首级网应尽量布设为网状，如果因条件受限无法将首级网布设为网状，那么应尽量减少导线点数量，以提高首级网的可靠性。在满足精度要求的前提下，可以采用整网平差代替两级网，以提高作业效率、降低作业成本。在试验中观测数量为2 个测回，采用适当增加测回数的方法可以进一步提高控制网的质量。试验中测量船舶为钢铁结构，测量时间为夏季，虽然选择在温度变化较小的夜间进行作业，但是其温度变化也达到3 ℃左右。船体控制点受热胀冷缩影响较大，这也是产生测量误差的一个主要因素，在实际应用中不能忽略。试验中对此进行验证，针对同一点位的坐标，采用同样的仪器和观测方法，坐标较差会超过1 cm，甚至更大，并且日间作业大气环境的变化较大，对全站仪观测数据质量也有较大影响。因此在实际应用中应充分考虑环境因素的综合影响，作业前宜使用精密几何水准对所使用的全站仪在实际作业场景条件（大气环境、视线长度以及垂直角等）下的三角高程测量精度进行验证。

3 结语

该文通过自由设站法构建的三维控制网以高精度的全站仪和靶球配合测量，可以为船舶测量，特别是船舶上安装在不同部位的精密设备相对定位提供精度较高的三维参考基准，并且以靶球中心为控制点可以直接与激光跟踪仪进行衔接，完成精密设备的安装、校准、定位和姿态测量工作。控制网以自由设站法进行观测，测站点是以仪器中心为控制点，避免了对中误差带来的精度损失。照准点以精密靶球中心为控制点，重复安置和照准精度高，无须量取仪器高和觇标高，可以提高高程控制的精度。该三维控制测量和平差模型具有精度高、布设灵活、作业简便和效率高等优势，可以为同类型精密工程测量的应用提供参考。