四旋翼无人机飞行控制算法设计及仿真分析

王建山 卢利中 丁 伟 张天宇 王光璞

（国网吉林省电力有限公司吉林供电公司，吉林 吉林 132012）

由于无人机技术日趋成熟，无人机逐渐成为一种新型智能装备，由于其具有灵巧度高、体积小以及可以定点悬停等特性，因此应用范围较广[1]。四旋翼飞行器因其独特的飞行方式，起降时所需空间较小，有利于在障碍物密集的环境中保持高机动性飞行。四旋翼无人机具备简单的机械构造，主要由十字形框架和4 个旋翼组成。当对其进行数学建模时可以发现，它是一个强耦合、非线性和欠驱动的六自由度系统。通过调整4 个螺旋桨的速度就可以实现不同的飞行姿态[2]。由于非线性强耦合系统的特性，因此控制四旋翼飞行器从初始位置到目标位置且保持当前运动状态比较困难[3]。为了达到该目的，需要对非线性四旋翼飞行器模型进行线性近似处理。该文研究了四旋翼飞行器的双闭环结构，将外环速度环的控制输入设置为内环角度环的输出，以实现对飞行器姿态进行控制的功能。该文分析了四旋翼的非线性模型和双闭环系统，建立了飞行器的动力学模型，在该模型的基础上，设计了双闭环控制系统，并采用MATLAB 进行控制系统稳定性仿真试验。

1 四旋翼无人机动力系统模型

无人机动力系统模型是四旋翼无人机飞行控制算法设计研究的基础，模型建立的准确性将直接影响控制算法设计的合理性和有效性。该文建立无人机位移运动方程、旋转运动方程、动力学方程和系统控制分配模型，为建立控制算法和搭建仿真平台奠定基础。

1.1 运动学方程

1.1.1 位移运动方程

在已知四旋翼无人机机体坐标系下的三维运动速度（u，v，z）的情况下[4]，可以采用旋转变换理论计算四旋翼无人机地面坐标系下的三维线运动速度（，，），如公式（1）所示。

式中：θ为俯仰角；γ为横滚角；φ为偏航角。

1.1.2 旋转运动

在已知四旋翼无人机机体坐标系下的三维姿态角速度（p，q，r）的情况下[5]，可以采用旋转变换理论计算四旋翼无人机地面坐标系下的三维线姿态角加速度（，，），如公式（2）所示。

1.2 动力学方程

采用Newton-Euler 式来推导飞行器的动力学方程[6]，动力学方程如公式（3）所示。

1.3 系统控制分配模型

飞行控制有升降运动、滚转运动、俯仰运动以及偏航运动4 种状态，由安装在翼端的4 个电机驱动螺旋桨转动完成，分别用U1～U4表示，如公式（4）所示。

式中：b为飞行器的桨叶的升力系数；d为飞行器桨叶的阻力系数；Ωi（i=1，2，3，4）为飞行器的电机转速。

2 控制算法设计

无人机控制算是整个飞行系统的控制核心[7]，决定无人机轨迹飞行的稳定性和安全性。随着无人机在各领域的广泛应用，无人机飞行控制算法受到了各国学者的广泛关注[8]，并取得了显著的研究成果。无人机飞行控制算法是无人机的大脑，一个好的控制算法可以保障无人机稳定、安全飞行[9]。目前，滑模控制算法和模糊控制算法是前沿研究理论，但是还未应用于实际工程中，当前普遍采用PID 算法完成位置控制器和姿态控制器算法的设计工作。

2.1 位置控制器算法设计

采用PID 算法求出四旋翼飞行器在地面坐标系下的线加速度，如公式（5）所示。

式中：zd为目标给定值；z为反馈高度；d为桨叶的阻力系数；kp3、kd3为2 个PD 算法参数。

通过俯仰角θ、横滚角γ得到飞行器的电机输入信号，如公式（6）所示。

式中：P1为飞行器的电机输入信号；g为重力加速度。

2.2 姿态控制器算法设计

采用PID 算法求出四旋翼飞行器的电机输入信号P2、P3和P4，分别如公式（7）～公式（9）所示。

式中：kpγ、kdγ、kiγ、kpθ、kdθ、kiθ、kpφ、kdφ和kiφ为9 个PID算法参数；eγ、eθ和eφ分别为飞行器的俯仰角、横滚角和偏航角的欧拉角。

3 仿真分析

四旋翼无人机初始欧拉角和初始欧拉角速度分别为（0，0，0）rad、（0，0，0）r/s；四旋翼无人机初始位置、初始线速度为分别为（0.1，0.1，1.0）m、（0，0，0）m/s。四旋翼无人机期望飞行位置为（0，0，1.26）m。

在MATLAB 软件中搭建了一个四旋翼仿真系统，以验证飞行器控制系统在无风和有风干扰下的稳定性。为了验证控制算法遇到有风干扰时的稳定性，分别在无风干扰和有风干扰2 种状况下对控制系统的稳定性进行仿真验证。有无东、北风干扰下的飞行器位置变化曲线如图1 所示，有无东、北风干扰的飞行器沿地面坐标系飞行速度曲线如图2 所示，有无东、北风干扰的飞行器姿态角响应曲线如图3 所示。

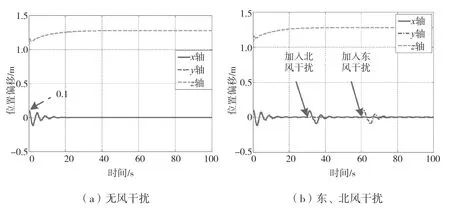
图1 有无东、北风干扰的飞行器沿地面坐标系飞行位置变化

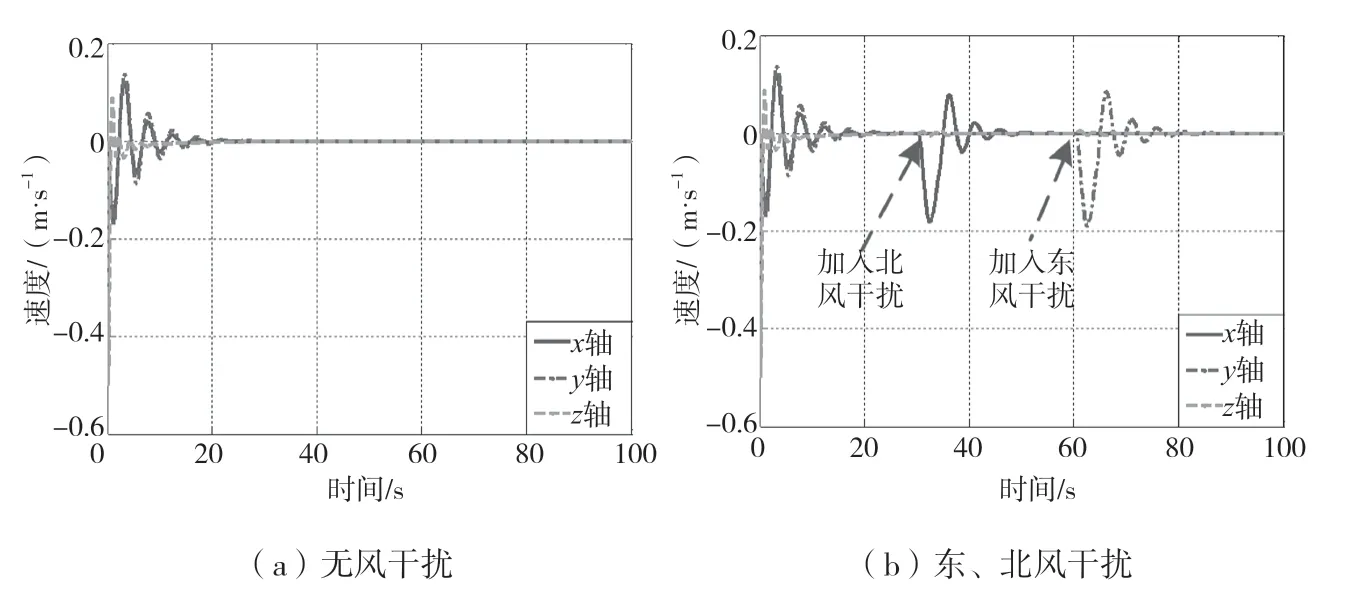
图2 有无东、北风干扰的飞行器沿地面坐标系飞行速度曲线

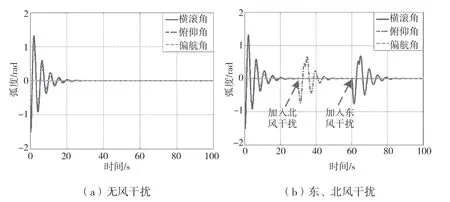
图3 有无东、北风干扰的飞行器姿态角响应曲线

由图1（a）可知，飞行器在起飞初始时刻的位置坐标为（0.1，0.1，1.0）。在经过20 s 的飞行后，飞行器成功达到目标坐标（0，0，1.26）处并保持了稳定的位置。整个系统确保了飞行器在期望的位置上进行稳定悬停飞行，说明控制算法在无风干扰下具有飞行稳定性，可以满足特定场景下的飞行任务。由图1（b）可知，在30 s 和60 s 的时间点，使用幅值为0.1、脉宽为4 s 的单脉冲方波模拟自然界的北风和东风干扰，导致飞行器在x轴和y轴上发生扰动。经过10 s，飞行器再次返回到目标位置（0，0，1.26）并保持不变。综上所述，在无风干扰的情况下，四旋翼飞行器可以准确执行飞行、悬停动作，当有风干扰时，飞行器在发生小的飞行扰动后依然可以抵达目标位置，说明控制算法具有有效性和合理性，可以保证飞行器在干扰下的飞行稳定性。

由图2（a）可知，在0 s～20 s 飞行器的速度波动较大，约20 s 时，速度接近0 m/s，表明此时飞行器已基本到达目标位置，其位置不再发生变化。整个飞行器控制系统确保了飞行器在期望的位置上进行稳定悬停飞行，说明控制算法在无风干扰下具有飞行稳定性。由图2（b）可知，飞行器在30 s 受到了北风干扰，在60 s 受到了东北风干扰，导致在x轴和y轴方向的速度发生扰动。然而，大约经过10 s 后，飞行器速度再次稳定为0 m/s，使其进入悬停状态，飞行器保持静默状态。综上所述，飞行器飞行速度抗干扰性较强，即使遇到较大的风干扰，也可以迅速调整恢复到设定飞行速度，保证飞行器执行任务时的飞行稳定性。

由图3（a）可知，飞行器的姿态角度在20 s 变为0°并保持稳定。整个飞行器控制系统系统确保了飞行器姿态的稳定，说明飞行器控制算法在无风干扰下具有飞行稳定性。由图3（b）可知，在30 s 施加北风干扰，然后在60 s施加东北风干扰，飞行器的俯仰角和横滚角受到一定强度的干扰。然而，经过约10 s 的时间，飞行器的姿态角恢复到初始的0°并保持了稳定的姿态角度。综上所述，飞行器飞行姿态抗干扰性较强，在经历干扰后可以迅速恢复到初始0°的位置，具有较高的飞行稳定性。

4 结语

该文采用Newton-Euler公式构建四旋翼无人机的动力系统模型，采用PID 控制算法设计了双闭环控制系统，并在MATLAB 软件中构建四旋翼仿真平台。仿真结果显示，设计的四旋翼无人机飞行控制系统可以抑制风干扰，具有较高的飞行稳定性，可以满足工程应用的设计要求。