形如4k-1、4k+1、6k-1和6k+1(k∈Z+)的素数都有无穷多个

陈 川,宓 玲

1.齐鲁工业大学(山东省科学院) 山东省计算中心(国家超级计算济南中心) 算力互联网与信息安全教育部重点实验室,山东 济南 250353; 2.山东省计算机网络重点实验室 山东省基础科学研究中心(计算机科学),山东 济南 250014; 3.齐鲁工业大学(山东省科学院) 数学与统计学院,山东 济南 250353

许多密码算法都建立在大素数的基础上,比如RSA公钥密码算法、ElGamal公钥密码算法、Rabin公钥密码算法、Diffie-Hellman密钥交换协议、Shamir门限密钥共享方案等[1]。特别地,在RSA、ElGamal和Rabin等公钥密码算法中,大素数或者是公钥的一部分,或者可用于生成公钥,每个用户拥有的大素数应各不相同,还需要定期更换。因此,密码学中对素数的需求量是非常大的。考虑到密码学的应用范围越来越广泛,因此有必要对素数个数和素数分布进行深入研究。

已知素数有无穷多个。若使用反证法,不难证明这个结论。另一方面,素数有非常多的分类方式。比如说,素数可以分为3种类型:2,形如4k+1的素数(5、13、17等),形如4k-1的素数(3、7、11等),其中k∈Z+。那么,形如4k-1和4k+1的素数是否分别有无穷多个?对该问题的研究具有现实意义:在Rabin公钥密码算法中,为保证顺利解密,只能使用形如4k-1的素数;在RSA公钥密码算法中,所使用的大素数一般都应是安全素数,大的安全素数也属于形如4k-1的素数。再比如说,素数还可以分为4种类型:2,3,形如6k+1的素数(7、17、19等),形如6k-1的素数(5、11、17等),其中k∈Z+。那么,形如6k-1和6k+1的素数是否分别有无穷多个?

“形如4k-1的素数有无穷多个”,该结论曾作为例题出现在教材中[2],然而例题的证明逻辑性不强,说服力不够。“形如4k+1的素数有无穷多个”和“形如6k-1的素数有无穷多个”,这两个结论曾作为课后习题出现在教材中[2-4],截至目前,笔者尚未见到这两个结论的证明。“形如6k+1的素数有无穷多个”,该结论的证明难度要更大一些,在证明该结论之前,本文先给出了一个有用的引理。

1 预备知识

定义1[5]已知p为素数,若(a,p)=1且同余式x2≡a(modp)有解,则称a为模p的平方剩余,否则称a为模p的平方非剩余。

定义2[5]设m>1是整数,a为正整数且(a,m)=1,则使得ax≡1(modm)成立的最小正整数x叫做a模m的阶,记为ordm(a)。

引理1(Euler判定法则)[5]设p是奇素数,(a,p)=1,则

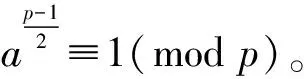
引理2[5]设m>1是整数,a为整数且(a,m)=1,若整数d使得ad≡1(modm),则有ordm(a)|d。

引理3(Euler定理)[5]设m>1是整数,a为整数且(a,m)=1,则aφ(m)≡1(modm),其中φ(m)表示m的Euler函数。

2 主要结果

定理1 形如4k-1(k∈Z+)的素数有无穷多个。

证明：(反证法)假设形如4k-1的素数仅有有限多个,不妨设有n个,分别为:p1,p2,…,pn,其中n为某个正整数。

构造一个新的整数:M=4p1p2…pn-1。

首先证明M不是素数。已知素数仅有3种类型:2,形如4k+1的素数,形如4k-1的素数,其中k∈Z+。(1)由于M是一个外在形式如4k-1的数,所以它不可能是2、形如4k+1的素数。(2)根据假设,形如4k-1的素数仅有p1,p2,…,pn,且M∉{p1,p2,…,pn},所以M也不可能是个形如4k-1的素数。综上,M不是素数,它是合数。

M既然是合数,它肯定存在素因子。M的素因子只可能属于3种类型:2,形如4k+1的素数,形如4k-1的素数,其中k∈Z+。显然,2M。另一方面,已假设形如4k-1的素数仅有p1,p2,…,pn,且易知p1M,p2M,…,pnM。由此可得,合数M的所有素因子不包括2,也不包括形如4k-1的素数,即M的所有素因子都是形如4k+1的素数。因此,M所有素因子的乘积与1模4同余。然而,M是与-1模4同余。矛盾。

所以,形如4k-1的素数有无穷多个。

引理4已知素数p>2,若-1是模p的平方剩余,则p≡1(mod 4)。

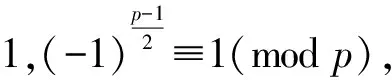
定理2形如4k+1(k∈Z+)的素数有无穷多个。

证明：(反证法)假设形如4k+1的素数仅有有限多个,不妨设有n个,分别为:p1,p2,…,pn,其中n为某个正整数。

构造一个新的整数:M=4(p1p2…pn)2+1。

首先证明M不是素数。已知素数仅有3种类型:2,形如4k+1的素数,形如4k-1的素数,其中k∈Z+。(1)由于M是一个外在形式如4k+1的数,所以它不可能是2、形如4k-1的素数。(2)根据假设,形如4k+1的素数仅有p1,p2,…,pn,且M∉{p1,p2,…,pn},所以M也不可能是个形如4k+1的素数。综上,M不是素数,它是合数。

M既然是合数,它肯定存在素因子。由于2M,可知M肯定存在大于2的素因子。

设q>2是M的一个素因子,则有M≡4(p1p2…pn)2+1≡0(modq),可得(2p1p2…pn)2≡-1(modq)。所以存在x≡2p1p2…pn(modq)且x∈{1,2,…,q-1},使得x2≡-1(modq),即-1是模q的平方剩余。由引理4可知,q≡1(mod 4)。这意味着M存在形如4k+1的素因子q。然而根据假设,形如4k+1的素数仅有p1,p2,…,pn,且易知p1M,p2M,…,pnM。矛盾。

所以,形如4k+1的素数有无穷多个。

定理3形如6k-1(k∈Z+)的素数有无穷多个。

证明：(反证法)假设形如6k-1的素数仅有有限多个,不妨设有n个,分别为:p1,p2,…,pn,其中n为某个正整数。

构造一个新的整数:M=(p1p2…pn)2-2。

首先证明M不是素数。已知素数包括4种类型:2,3,形如6k+1的素数,形如6k-1的素数,其中k∈Z+。(1)由于M是一个外在形式如6k-1的数,所以它不可能是2、3、形如6k+1的素数。(2)根据假设,形如6k-1的素数仅有p1,p2,…,pn,且M∉{p1,p2,…,pn},所以M也不可能是个形如6k-1的素数。综上可知,M不是素数,它是合数。

M既然是合数,它肯定存在素因子。由于M是一个外在形式如6k-1的数,因此2M且3M,可知M肯定存在大于3的素因子。设q>3是M的一个素因子,则q是形如6k+1或6k-1的素数。所以,M的素因子或者形如6k+1,或者形如6k-1。

接下来证明:M的素因子不可能全都形如6k+1。若M的素因子全都形如6k+1,则M所有素因子的乘积与1模6同余,而M是与-1模6同余,矛盾。

综上可得,M至少存在一个形如6k-1的素因子。然而根据假设,形如6k-1的素数仅有p1,p2,…,pn,且易知p1M,p2M,…,pnM。矛盾。

所以,形如6k-1的素数有无穷多个。

引理5设素数p>3是x2-x+1(x∈Z)的因子,则p≡1(mod 6)。

证明：首先证明(x,p)=1。若(x,p)≠1,则p|x,因此x≡0(modp),所以x2-x+1≡0-0+1≡1(modp)。然而,根据已知条件x2-x+1≡0(modp)。矛盾。

(1)证明ordp(x)≠1。若ordp(x)=1,则x1≡1(modp),所以x2-x+1≡1-1+1≡1(modp)。然而,根据已知条件x2-x+1≡0(modp)。矛盾。

(2)证明ordp(x)≠2。若ordp(x)=2,则x1≢1(modp)且x2≡1(modp)。由x2≡1(modp)可知,x≡±1(modp),又因x≢1(modp),可得x≡-1(modp),因此x2-x+1≡1+1+1≡3(modp)。然而,根据已知条件x2-x+1≡0(modp)。矛盾。

综上可知,ordp(x)=6。

因为(x,p)=1,由引理3可知xφ(p)≡xp-1≡1(modp)。根据引理2,ordp(x)|p-1,即6|p-1。因此,p≡1(mod 6)。

定理4形如6k+1(k∈Z+)的素数有无穷多个。

证明：(反证法)假设形如6k+1的素数仅有有限多个,不妨设有n个,分别为:p1,p2,…,pn,其中n为某个正整数。

由p1≡1(mod 6),p2≡1(mod 6),…,pn≡1(mod 6)可知,p1p2…pn≡1(mod 6),所以M≡1-1+1≡1(mod 6)。

首先证明M不是素数。已知素数包括4种类型:2,3,形如6k+1的素数,形如6k-1的素数,其中k∈Z+。(1)由于M是一个外在形式如6k+1的数,所以它不可能是2、3、形如6k-1的素数。(2)根据假设,形如6k+1的素数仅有p1,p2,…,pn,且M∉{p1,p2,…,pn},所以M也不可能是个形如6k+1的素数。综上可知,M不是素数,它是合数。

M既然是合数,它肯定存在素因子。由于M是一个外在形式如6k+1的数,因此2M且3M,可知M肯定存在大于3的素因子。设q>3是M的一个素因子。根据引理5,q≡1(mod 6),即M存在一个形如6k+1的素因子q。然而根据假设,形如6k+1的素数仅有p1,p2,…,pn,且易知p1M,p2M,…,pnM。矛盾。

所以,形如6k+1的素数有无穷多个。