有理数加法学习的认知模拟研究

崔 硕，崔丽红，连四清

有理数加法学习的认知模拟研究

崔 硕，崔丽红，连四清

（首都师范大学 数学科学学院，北京 100048）

在有理数加法运算中，正、负两数相加且结果为负的情形是学生学习的难点．研究应用认知模拟方法探索有理数加法的盈亏模型和绝对值模型的认知过程及其差异，结果表明：当工作记忆能力较弱，表征用时较长时，运用绝对值模型计算有理数加法的用时超过盈亏模型．两模型的差异源于问题表征的次数、问题和知识的表征形式以及对前备知识的熟练程度3个方面．盈亏模型基于熟悉的现实背景，问题及知识表征的次数少、形式简单，减轻了学习的认知负荷．建议学生在初学阶段直接利用盈亏模型进行有理数加法运算，在理解的基础上逐步总结运算规律．

ACT-R；认知模拟；有理数加法

1 问题提出

ACT-R（Adaptive Control of Thought-Rational）理论由Anderson等人提出，通过建立ACT-R模型并在计算机上模拟，解释人类的学习、记忆、问题解决等认知行为．将ACT-R模型应用于数学教育，可以预测学生已经具备的知识、能力以及达成学习目标的关键步骤，解释数学学习的认知过程[1]．

在数学认知研究中，数与代数是培养学生抽象与概括、论证与表征能力的重要载体[2]．Anderson等人最先将ACT-R模型应用于代数认知领域[3]，模拟了两步线性方程的求解过程．通过比较学生第1～5天的模拟学习数据，揭示了实现解方程自动化的关键步骤，从而得出解方程过程的加速主要源于产生式合并和对算术知识的熟练提取两个方面．代数运算以算术运算为基础，关于算术运算的认知研究主要集中于运算法则的学习过程．Bethany等人运用ACT-R模拟了学习分数除法法则的两种策略：基于分数和除法意义的“图形分割”策略和基于运算程序的“取倒数相乘”策略[4]．通过对所提取知识和认知步骤的分析，从学习难度、应用效率、通用性、记忆和可迁移性等维度比较了两种策略．结果表明：学习的难易程度取决于对先验知识的掌握情况；记忆基于“传播激活”的学习机制，当具有熟悉且丰富的相关背景知识时，学习策略更易于回忆．上述研究可推广为对运算法则学习策略的一般性讨论：在学习初期，应注重从知识背景中理解和获取运算法则，还是侧重于记忆和执行计算程序？

有理数加法是学生学习的第一种有理数运算，加法法则中的符号规则是学生学习的难点．多数教材中以位移等具有相反意义的现实情境导入，引导学生将现实情境抽象为运算表达，由算式归纳出有理数加法法则．学生需要运用归纳出的法则，才能进行有理数加法运算．问题情境影响着学生的知识建构和思维发展[5]．陈丽敏等人研究了问题情境对学生建构有理数加法法则的影响，表明：学生由这些情境建构有理数加法法则时，存在共同的认知困难[6]．其原因主要有两方面：一方面，学生未达到将意义相反的量统一并选择正确的运算解决问题的认知水平，导致学生直接由现实情境列出加法算式存在困难；另一方面，语义复杂的现实情境影响了学生对加法意义的迁移，使学生在选择使用哪种运算时出错．在学习代数运算的初期，学生更倾向于直接在简单的现实情境中解决问题，随着学习的深入，当情境和计算较复杂时，才逐渐归纳出代数表达式和运算法则[7]．

如果有理数加法以数轴、绝对值的掌握与应用为基础，由于几何知识尚不完善，学生无法熟练建立绝对值与数轴之间的联系，对绝对值的认知仍存在问题[8]；在建构法则的过程中，学生要同时处理现实情境、数轴及数学语言这3类相关性较强的信息；在应用法则的过程中，学生不但要进行绝对值的比较和运算，而且要在工作记忆中同时保持算式、两个加数的绝对值、正负数符号等信息．由于工作记忆容量有限，上述过程可能会增加学生的认知负荷，从而影响学生的学习．

综上，综合考虑学生的认知发展水平与代数学习的应用价值[9]，提出新想法：通过情境简单、易于理解的现实模型来实现有理数加法表达．学生通过将有理数加法转化为现实模型，理解有理数加法运算及结果；随着理解加深和运算的熟练，逐步归纳出有理数加法法则的代数表达．基于此，运用ACT-R模型对学生学习有理数加法的认知过程进行模拟，验证模型的合理性，并揭示学习有理数加法的预备知识以及关键步骤．通过比较盈亏模型与绝对值模型的模拟数据，分析两种模型的认知过程差异及适用条件，从而为实证研究和教学实践提供参考．

2 有理数加法学习的认知模型

2.1 盈亏模型

一个有理数与0相加的运算法则是易于理解和掌握的，所以接下来重点讨论两非零有理数相加的情形．在有理数加法教学中，可以借助盈亏模型辅助学生理解有理数加法的符号法则．

当识别有理数加法运算的数学表达式后，首先将数学表达式转化为盈亏问题，接着在盈亏模型中进行计算，最后将盈亏结果转为数学表达，即得到两个有理数的和．盈亏模型是易于理解的现实模型，如一家商店的盈利为“正”，亏损为“负”．若两次连续亏损，则合计为亏损，且亏损金额为两次亏损金额之和；若两次中有盈利有亏损，则比较盈利金额与亏损金额．若盈利金额大于亏损金额，则合计为盈利，总的盈利金额为盈利金额减去亏损金额等．

运用盈亏模型进行两非零有理数加法运算的过程可表示为如下程序框图（图1）．

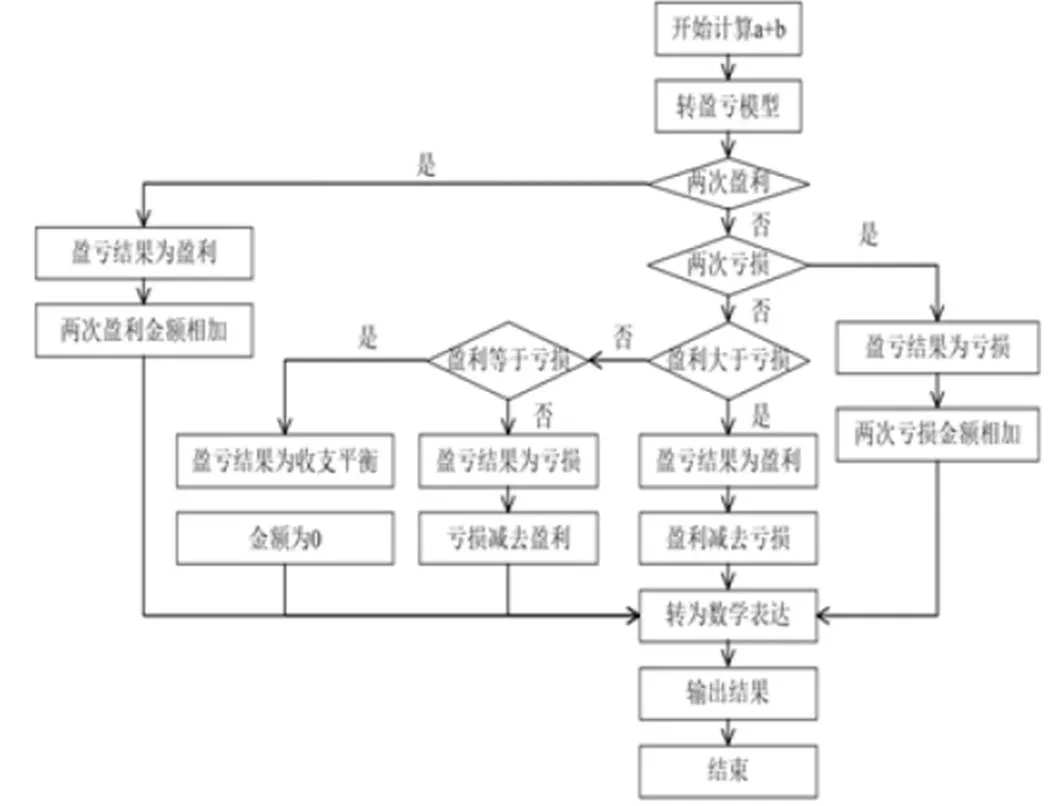
图1 有理数加法运算模型程序框图

由图1可以看出，在盈亏模型中，有盈有亏且盈利小于亏损的情形最为复杂，其思维步骤遍历了其它情形，与之相对应的是两个有理数的加法中正数加负数且和为负数的情况．因此，以“正数加负数且和为负数”的情况为例，依据ACT-R理论对盈亏模型与绝对值模型进行认知模拟．由于绝对值模型已被熟知，且篇幅限制，在此不对其过多赘述．

2.2 知识表示

习得有理数加法法则离不开已经具备的知识，模型的建立从对问题和知识的编码开始．以计算“(+6)+(-10)”为例，使用“盈亏模型”和“绝对值模型”都需要解析算式和自然数运算事实等知识，而与模型背景相关的知识有所不同．此外，在不同认知基础下，对同一知识或问题的表征也会有所不同．在ACT-R模型中，这些前备知识可表征为陈述性知识，在块（chunk）中存储．计算“(+6)+(-10)”的所有陈述性知识编码如表1所示．模型通过产生式提取和解释上述知识，完成解题过程．如表2所示，产生式系统包括通用性指令，和表达特定策略和提取特定知识的产生式．

产生式条件对应着工作记忆中的信息，即系统当前正在加工的信息[10]．以“代数表达转盈亏模型”产生式P5为例：条件中的“用盈亏模型计算两有理数之和”对应工作记忆中的当前目标，“已知两加数的正负数符号”对应问题表征．当满足产生式条件时，执行产生式的动作：将“两加数的正负数符号”添加到工作记忆中，提取长时记忆中相匹配的盈亏知识．提取到的知识在工作记忆中存储，以供下一条产生式使用．产生式系统可视为问题解决认知过程的直观化体现，通过计算机模拟，若产生式系统可以顺利运行，则证明了学习模型的可行性．

3 有理数加法学习模型的计算机模拟

3.1 认知模拟

Anderson团队基于Lisp语言开发了ACT-R7.0软件，其内部架构和参数以核磁共振实验数据为基础而设定．Adrian Bras-oveanu等人在此基础上使用Python语言开发了Pyactr包，提高了语言兼容性[11]．调用Python3.7中的Pyactr包，将表1知识表示和表2产生式系统编写为程序，模拟两种模型计算“(+6)+(-10)”的过程．计算分为编码、求解和响应3个阶段，由目标、程序、提取和表象模块相互作用而完成．以盈亏模型为例：在编码阶段，表象模块将“(+6)+(-10)”编码为心理表征．产生式识别到问题状态并激活求解策略，进入求解阶段．首先将正负数符号与算术数分开，解析算式为“+，6，+，-，10”；接着，将算式转为盈亏情境“盈利6元又亏损10元”，根据情境得出结果“亏损4元”；最后，将盈亏结果转为数学表达“-4”．这一过程通过提取模块提取盈亏情境、计算等陈述性知识，通过表象模块更新问题表征．在响应阶段，程序模块识别并输出运算结果．绝对值模型即为应用加法法则进行计算，不再赘述．

城里，我遇到老K，讲了这件事。老K不屑地说，没脸了呗，弄了个家破人亡，妻离子散，自己倒成了一个屯子人了。自作自受！

图2模拟了不同单次表征时间下，盈亏模型和绝对值模型完成有理数加法运算所需的时间．可以看出，在两个模型中，总的运算时间都随着单次表征用时的增加而增加．特别地，绝对值模型的运算时间增速更快，当单次表征用时0 s时，绝对值模型运算时间小于盈亏模型，单次表征用时0.10 s时，两模型运算时间相等，单次表征用时超过0.10 s时，绝对值模型运算时间更长．

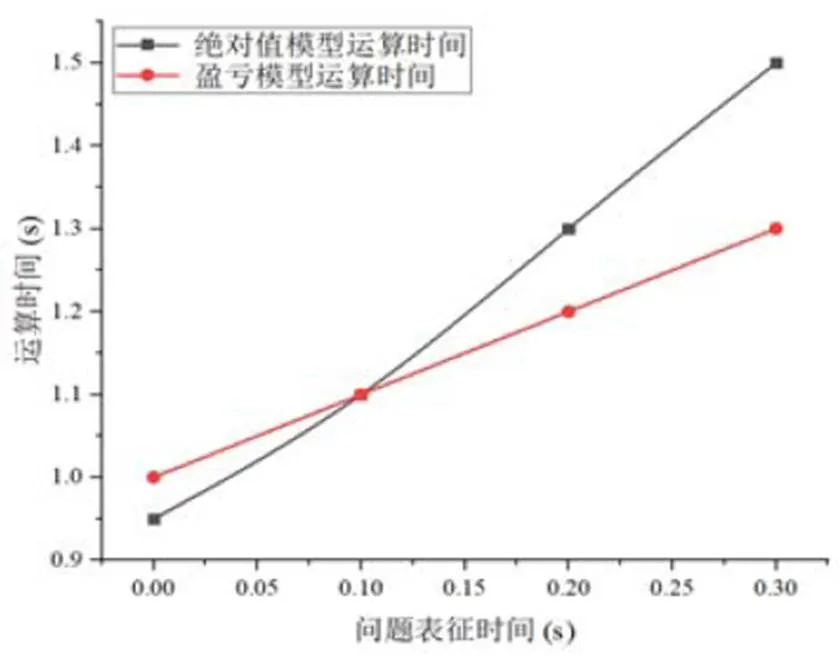
图2 两种模型完成运算所需时间

图3是问题表征时间为默认值0.2 s时的模拟实验数据．图3a为使用盈亏模型的模拟结果，图3b为使用绝对值模型的模拟结果．图中第一列是模拟时间，默认执行每条产生式、每次提取知识历时0.05 s，第二至五列说明了当前被激活的模块及在激活时间内所处理的信息．盈亏模型共用时1.20 s，绝对值模型共用时1.30 s．

比较两个模型的各个模块的结果如下．

（1）程序性模块．两个模型各激活了13条产生式．产生式系统可以顺利运行，证明了学习模型的可行性．虽然激活的产生式数量相同，但绝对值模型的运算程序中包含较多新习得的产生式，而盈亏模型中的产生式大多基于熟悉的现实背景．根据效用理论[12]，盈亏模型的产生式效用值更高，更容易运行成功．

（2）提取．两个模型都提取了解析算式和正有理数比大小以及加减运算等知识．不同之处在于，盈亏模型还提取了“盈亏与正负数符号互化”的知识；而绝对值模型提取了“求有理数绝对值”的知识．在模拟中，每次提取用时0.05 s，但实际上，知识的表征形式和对知识的熟练程度影响着提取效率[1]．如图3，两个模型虽然都提取到“比较6与10大小”的知识，但在工作记忆中的表征形式不同．在盈亏模型中，只需提取“小于”关系，而在绝对值模型中要同时提取大小关系、较大数和较小数．相比起来，盈亏模型的知识表征简单，占用的信息组块少，因而认知负荷较低，更利于提取．在熟练程度上，“用正负数符号表示具有相反意义的量”易于理解，因而“盈亏与正负数符号互化”是简单熟悉的知识；而“求有理数绝对值”是新习得的知识且更为抽象，提取时间更长．

（3）问题状态模块．该模块的缓冲区保持了运算过程中各阶段的问题表征．该模块每次只能建立一个问题表征，且建立新的表征需要时间，默认值为0.2 s（可通过参数更改）．图3为模型在默认值下的运行结果．从问题表征次数来看，盈亏模型中，问题表征发生了6次更改；绝对值模型中问题表征发生了7次更改．注意到，在绝对值模型中，若要“比较符号”，需将有理数表征为正负数符号与算术数分开的形式，即将“(+6)+(-10)”转化为“+，6，+，-，10”；若要求绝对值，则需重新提取算式“(+6)+(-10)”．多种表征形式的转换，导致信息加工速度减慢．从问题表征形式来看，绝对值模型中“确定符号”和“计算”的过程，都需要在工作记忆中同时保持加法算式、绝对值、符号关系和数字大小关系等信息，由于工作记忆容量有限，增加了认知负荷．数学能力较弱的学生工作记忆容量更小、知识提取所需时间更长．若调整模型参数，增加问题表征的时间，绝对值模型的认知负荷更大，计算用时更长．由此可以预测，对于数学能力较弱的学生来说，使用绝对值模型会更加困难，盈亏模型的问题表征形式简单，更利于掌握．

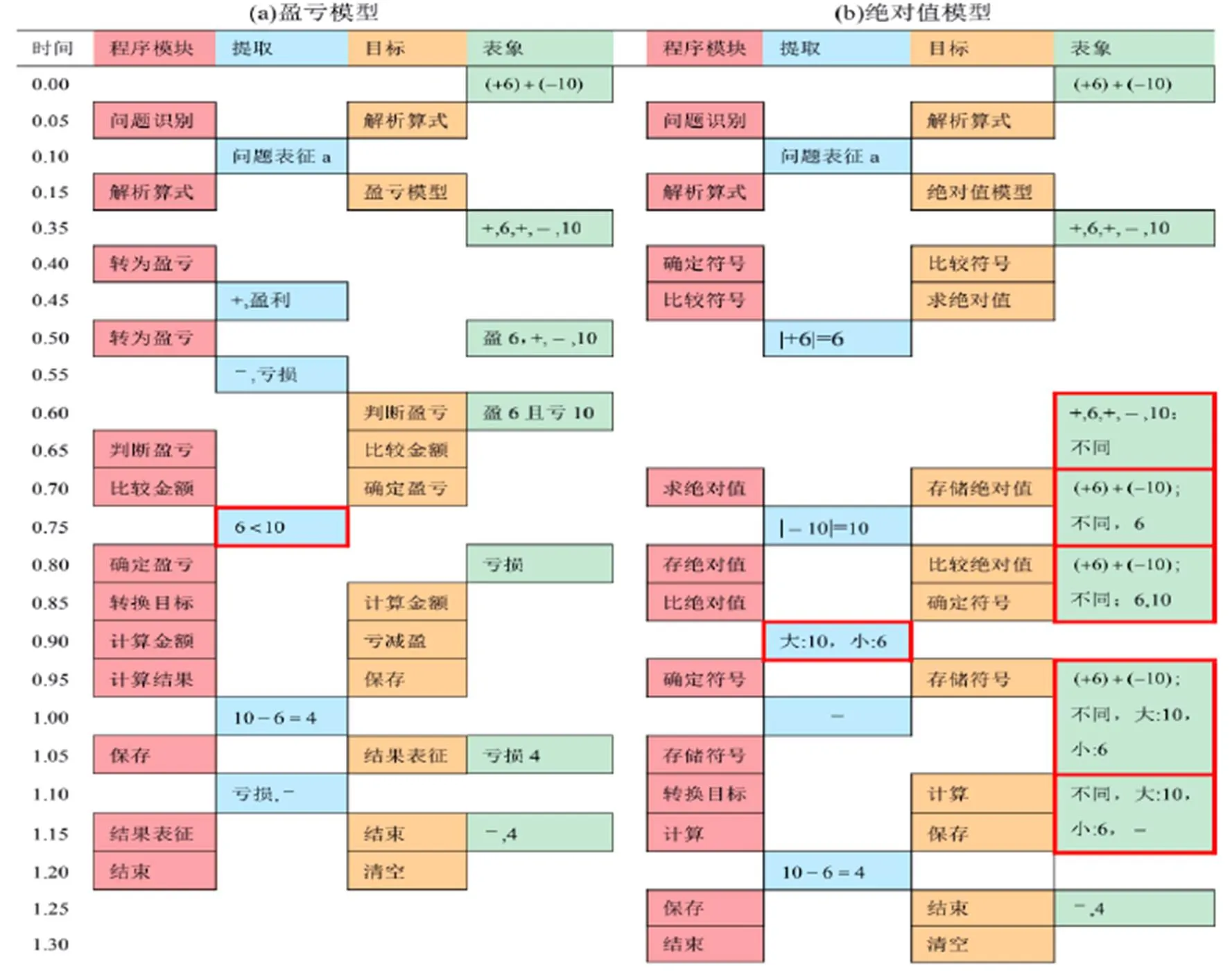
图3 盈亏模型（a）与绝对值模型（b）在ACT-R中的模块激活比较

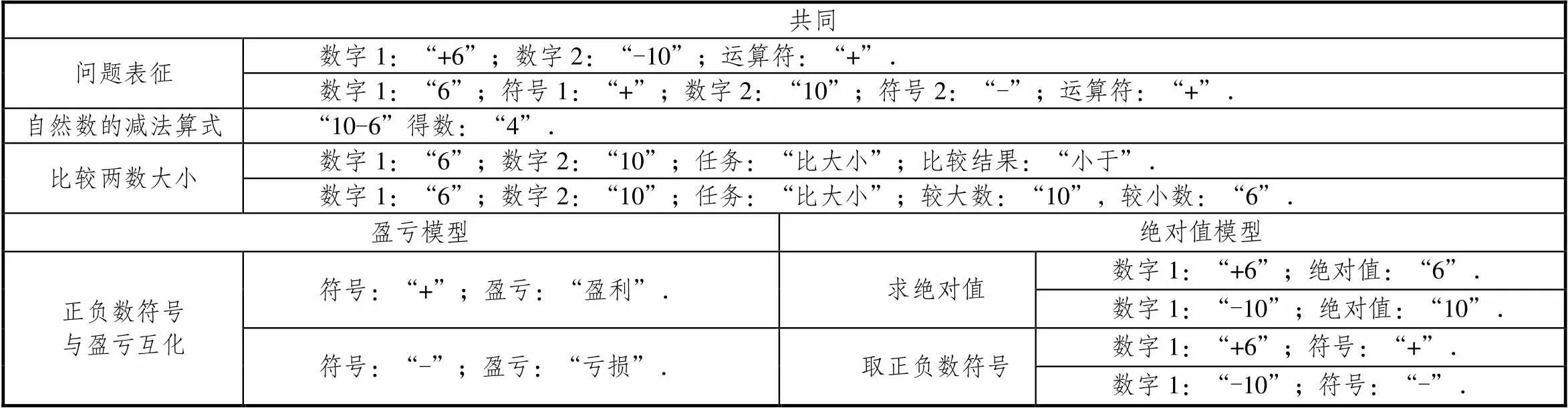
表1 问题表征和陈述性知识编码

表2 有理数加法运算产生式系统

3.2 分析与讨论

两模型的认知过程不同导致了认知负荷的差异，从而影响运算时间．其中，差异的来源主要有3个方面．第一，问题表征的次数；绝对值模型进行了多次问题表征和表征间的转换，增加了认知负荷．第二，问题和知识表征的形式[14]；绝对值模型对算式、绝对值、数字大小关系等信息的表征较复杂，会占用过多信息组块，不利于提取和在工作记忆中保持．第三，前备知识的掌握程度；对知识的掌握越熟练，越容易成功提取，反之则会导致用时过长或失败；绝对值概念是学生新习得的知识，且具有抽象性，相较而言盈亏知识是熟悉的现实背景，更易于提取．

由于工作记忆影响数学学习[15]，可以推测，这种差异对于数学能力弱的学生来说更加明显．因此，在有理数加法运算的教学中，为减轻学生的认知负荷，可暂且不使用绝对值的概念．通过盈亏模型来帮助学生理解有理数加法运算．采用把正负数符号与算术数分开的策略进行加法运算．初学阶段学生可直接利用盈亏模型进行有理数加法运算，在理解的基础上逐步总结运算规律．

上述研究的计算机模拟数据有待通过实证研究进一步验证，由于篇幅限制，将在后续的研究中加以补充．

4 研究结论

应用认知模拟方法探索了有理数加法的盈亏模型和绝对值模型的认知过程及其差异，由模拟结果得出以下结论．

（1）当工作记忆能力较弱，单次表征用时较长时，运用绝对值模型计算有理数加法的认知负荷较大，运算用时更长．

（2）两模型的差异源于问题表征的次数、问题和知识表征的形式以及对前备知识的熟练程度3个方面．盈亏模型基于熟悉的现实背景，问题及知识表征的次数少、形式简单，减轻了学习的认知负荷．

[1] Anderson J R. Cognitive tutor: Applied research in mathematics education [J]. Psychonomic Bulletin & Review, 2007, 14 (2): 249-255.

[2] 孙思雨，许添舒，孔企平．基于潜在类别分析的小学生早期代数思维水平研究[J]．数学教育学报，2022，31（1）：52-58．

[3] Anderson J R. Human symbol manipulation within an integrated cognitive architecture [J]. Cognitive Science, 2005, 29 (3): 313-341.

[4] Rittle-Johnson B, Koedinger K R. Using cognitive models to guide instructional design: The case of fraction division [C] // Mahwah. In Proceedings of the 23rd Annual Conference of the Cognitive Science Society. NJ: Erlbaum, 2001: 857-862.

[5] 张晶，夏小刚．数学问题情境化设计中的认知偏差及任务靶向[J]．数学教育学报，2022，31（6）：75-79．

[6] 陈丽敏，景敏．问题情境对学生建构有理数加法法则影响的差异性研究[J]．数学教育学报，2015，24（6）：64-67．

[7] Koedinger K R, Anderson J R. Illustrating principled design: The early evolution of a cognitive tutor for algebra symbolization [J]. Interactive Learning Environments, 1998, 5 (1): 161-179.

[8] 黄波．初中生绝对值概念认知状况的研究[D]．桂林：广西师范大学，2012：32．

[9] 石义娜，丁红云，夏小刚．初中数学教材中的问题编写及其价值取向变化——以人教版（1978—2020年）“有理数”内容为例[J]．数学教育学报，2022，31（2）：35-39．

[10] Anderson J R. Rule of the mind [M]. Hillsdale, NJ: Erlbaum, 1993: 1, 4-7.

[11] Adrian B, Jakub Dotlačil. Computational cognitive modeling and linguistic theory [M]. Switzerland: Springer, 2020: 7-15.

[12] Lovett M C, Anderson J R. History of success and current context in problem solving: Combined influences on operator selection [J]. Cognitive Psychology, 1996, 31 (2): 168-217.

[13] 郑毓信．《义务教育数学课程标准（2022年版）》的理论审思[J]．数学教育学报，2022，31（6）：1-5．

[14] 贺李，张春莉．脑科学对数学认知的最新研究成果及其教育启示[J]．数学教育学报，2023，32（1）：59-65．

[15] 林洪新，马荃，管晓，等．数学在线样例学习中的工作记忆资源损耗效应[J]．数学教育学报，2022，31（6）：24-29．

A Cognitive Simulation Study of Rational Number Addition Learning

CUI Shuo, CUI Li-hong, LIAN Si-qing

(School of Mathematical Sciences, Capital Normal University, Beijing 100048, China)

In the operation of rational number addition, it is difficult for students to learn the situation where positive and negative numbers are added and the result is negative. This study applies cognitive simulation methods to explore the cognitive processes and differences between the profit-and-loss model and the absolute value model of rational number addition. The results show that when the working memory capacity is weak and the representation takes longer, the use of the absolute value model to calculate the rational number addition takes longer than the profit-and-loss model. The differences between the two models stem from three aspects: the number of problem representation, the representation form of problems and knowledge, and the proficiency of prerequisite knowledge. The profit-and-loss model is based on a familiar real-life background, with fewer representations and simpler forms of representation, which reduces the cognitive load of learning. It is recommended that students use the profit-and-loss model to perform rational number addition operations directly at the beginning stage, and gradually summarize the operation rules on the basis of understanding.

ACT-R; cognitive simulation; rational addition

G632

A

1004–9894（2023）06–0067–05

崔硕，崔丽红，连四清．有理数加法学习的认知模拟研究[J]．数学教育学报，2023，32（6）：67-71．

2023–10–27

国家社科基金教育学重点课题——教师核心素养和能力建设研究（AFA170008）

崔硕（1994—），女，河北保定人，博士生，主要从事数学认知发展与教育研究．连四清为本文通讯作者．

[责任编校：陈隽、陈汉君]