多扰动下微电网故障检测方法

喻贞楷，王 斌，闫 墉，徐万万，方宇辰

（1. 武汉科技大学信息科学与工程学院，武汉 430081；2. 冶金自动化与检测技术教育部工程研究中心，武汉 430081）

微电网作为利用清洁能源的一种形式，其将光伏、风电及储能等通过现代电力电子技术连接在一起，并直接向用户端供电，得到广泛应用[1]。但随着大量分布式电源DG（distributed generation）并入配电网，逆变器等电力电子设备的大量使用会对故障分析和故障诊断产生影响，例如逆变器的限流保护作用使得故障电流受限、谐波复杂，进而导致故障特征不明显，同时复杂的运行状态也会严重影响故障诊断的正确性[2]。因此，高效精准的故障检测方法对维持微电网安全运行、提高供电可靠性有重要意义。

现有的电网故障检测方法主要分为两类：①基于电气信号稳态特征量的故障检测方法[3-4]，其原理是利用故障时产生的电流稳态工频信号的幅值、极性及功率方向来进行故障检测，但是由于不稳定电弧及故障间歇性的影响，容易造成稳态故障特征薄弱，从而造成稳定特征量检测法发生误判；②基于信号暂态特征量的故障检测方法[5-7]，其原理是利用故障发生时持续若干周波的暂态过程来进行故障检测，虽然故障发生时间短，但暂态过程信息丰富，并且不同的故障点、故障过渡电阻、运行工况等对应的暂态故障信息也是不同的。因此，以暂态故障信息数据为驱动的故障检测方法更加可靠准确。

随着数学理论及信号分解技术的发展，学者利用适当的故障信号分析方法来挖掘其隐含在暂态特征量中的故障信息，从而实现故障的有效诊断。目前常用的信号分析方法主要有小波变换、傅里叶变换、局部均值分解、经验模态分解等。其中，小波变换可以对故障信号进行任意放大及平移以提取相应特征。文献[8]利用快速小波变换对采集电流进行故障特征提取，随后利用极限学习机进行学习，得到故障诊断结果，但此类方法在选取不同小波基和分解尺度时会造成故障特征缺失，当发生高阻故障且故障特征薄弱时，往往会发生误判。而基于递归的经验模态分解方法有效解决了小波基选择问题，文献[9]利用经验模态分解对三相及零序电流进行分解，选取暂态高频信号的标准差和相关系数构造成故障特征量，将其在二进制蚁群模糊神经网络中学习以实现故障诊断，但该方法属于递归类模态分解，分解过程中极易出现模态混叠等问题，掩盖了信号微弱的故障特征，从而影响最终的故障诊断效果。针对上述问题，有学者将变分模态分解VMD（variational mode decomposition）[10]算法引入到故障信号分析中，有效地解决了传统信号分析的模态混叠问题。

如果采集的故障信号比较复杂，当故障特征薄弱时，不易直接获取较好的信号特征。若将原始信号直接进行神经网络学习，则容易因样本数大、计算复杂、学习时间长等问题影响最终的故障识别分类。熵用来衡量信号复杂度，常用的熵值算法包括样本熵、近似熵、排列熵PE（permutation entropy）及多尺度排列熵MPE（multiscale permutation entropy）。相比于其他熵值算法，MPE 对信号变化具有较高的敏感性，在信号程度更为复杂的脑电、地震波及机械方面[11]都取得了良好的辨识效果，但目前在电气故障识别方面鲜有运用。

为此，本文将VMD和MPE相结合，对运行状况复杂的微电网系统故障进行诊断。首先，通过逐次变分模态分解SVMD（successive variational mode decomposition）[12]将故障信号自适应分解为不同中心频率的模态分量；然后，利用峭度指数选择最优的模态分量，获取其MPE 以构成相应故障的特征量，用以表征不同故障情况下的故障特征；接着将故障特征量输入至基于鲸鱼算法优化核极限学习机WOA-KLEM（whale optimization algorithm-kernel extreme learning machine）模型进行训练。将训练好的WOA-KLEM 模型作为微电网故障诊断模型，进行微电网故障检测。

1 微电网对传统故障检测与保护的影响

不同于火电、水电等传统发电形式，DG受环境、天气与时间影响很大，出力存在很大的波动性，造成微电网系统不稳定运行，从而造成继电保护误动。另一方面，微电网存在并网运行、孤岛运行、孤岛环网及孤岛树状多种运行方式。不同运行状态下，微电网的短路电流存在着较大差异。当离网运行时，微电网多由逆变型DG 组成，逆变器等电力电子设备的限流作用使DG提供的短路电流为额定电流的1.2～2.0倍，导致短路电流较小；而当并网运行时，配网容量远远大于微电网，致使故障电流较大。可见，传统的单一阈值过流保护不再适用于微电网。

综上所述，微电网复杂的运行状态、DG频繁投切、DG出力波动等都对微电网故障诊断产生影响，从而影响微电网保护的可靠性。因此，需要一种既能适应微网不同运行状态，又能准确辨别故障扰动与非故障扰动的故障检测方法，为微电网故障保护提供更加精准的故障诊断信息。

2 算法介绍

2.1 变分模态分解

VMD是2014年由Dragomiretskiy等提出的一种完全非递归、准正交的信号分解算法，其核心思想是将传统的信号分解转变为变分求解问题，通过对变分模型寻找最优解来进行信号分解，到K个模态分量，分解后的模态不仅要满足全部模态之和与原始信号相等，而且要求每个模态函数的估计带宽之和达到最小。

约束变分问题可表示为

式中：{uk} 为分解后K个模态分量的合集；{ωk} 为分解后模态分量的中心频率的合集；δ(t) 为狄拉克分布；为模态函数uk(t) 对应中心频率ωk的指数项；为分解后所有模态分量之和；uk(t) 为分解后第k个模态分量；f(t) 为原始信号；∂t表示求偏导运算。

通过引入拉格朗日乘数λ和二次项惩罚因子α将式（1）所示的约束变分问题转变为非约束变分问题，并得到增广拉格朗日表达式，即

式中：λ(t) 为拉格朗日算子；表示内积运算。

2.2 逐次变分模态分解

尽管SVMD 具有良好的信号分解能力，但其分解效果取决于参数K与惩罚因子α的取值，当K过小时，易导致信号分解不足，信号中部分分量互相夹杂；而当K过大时，会使得信号分解过度，信号的重要分量由2个或多个不同模式共享，呈现过分解状态。 因此，在使用SVMD进行信号分解时，需预先确定合适的K值。为了能自适应分解K值，为此，本文在利用SVMD算法分解信号的过程中加入准则约束。

（1）由于每个被分解的子模态都围绕一个中心频率，故在信号分解过程中加入最小化约束，即

式中：J1为第1 个约束条件；ωL为第L阶模态的中心频率。

（2）为了使分解后的模态分量与残余未分解的模态分量之间模态频谱重叠量最小，可选用满足如下频率响应的滤波器：

根据式（4）可得第2个分解约束J2为

式中：fr(t) 为残余未分解的模态分量；* 表示卷积运算；βL(t) 为式（4）中滤波器的脉冲响应。

（3）为了有效区分第L阶模态与前L-1阶模态，可选用满足如下频率响应的滤波器：

根据式（6）可得第3个分解约束J3为

式中，βi(t) 为式（6）中滤波器的脉冲响应。

（4）为了确保信号能够完全重构，分解后的信号应满足前L-1 阶模态分量、第L阶模态分量与残余未分解的模态分量之和等于原信号，即

因此，分解信号获取模态问题可以表示为满足上述约束条件下的最小化解问题，即

式中，τ为平衡3个约束条件J1、J2和J3的参数。

2.3 多尺度排列熵

为了精确反映信号复杂度，避免微弱信号特征遗失，Aziz 等提出了MPE 的概念，利用不同尺度下的排列熵表征信号的复杂度，对信号突变及微弱变化更敏感。MPE的计算过程如下。

（1）对于给定信号xi(i= 1,2,…,N) 进行多个粗粒化处理，即

式中：s为尺度因子；j= 1，2，…，N/s，N为信号序列时间长度；ys(j) 为粗粒化后不同尺度下的信号序列。

（2）对每个粗粒化后的信号序列进行相空间重构，以得到序列重新构建的分量，即

式中：Ys(i) 为对xi粗粒化相空间重构后的分量；i为重构分量数；m为嵌入维数；τ为延迟时间。

（3）将重构分量Ys(i) 按照升序方式排序，由重构分量组成的新序列S(r) 可表示为

式中：r= 1，2，…，K，K≤m!；jm为排序后的重构分量。

（4）计算每个序列S出现的概率，并根据信息熵的定义对其加以标记。粗粒化序列的排列熵可表示为

式中：Hp为排列熵值；Pr为序列出现概率。

3 基于SVMD-MPE 的微电网故障特征提取

考虑到微电网的故障信号具有非线性、非平稳、故障特征薄弱等特点，本文提出了一种基于逐次模态分解与多尺度排列熵相结合SVMD-MPE（successive variational mode decomposition-multiscale permutation entropy）的故障信号特征提取方法。首先采用SVMD 算法将各继电器采集到的故障前后各半个周期内的故障电压信号自适应分解成多个模态分量；接着引入峭度对其模态分量进行优化重构；然后计算优化重构信号的MPE，从而实现故障信号特征的定量描述。该方法既能充分发挥SVMD算法自适应分解信号的特点，又能多尺度刻画故障信号的局部特征，实现了故障信号特征的全新表征。

故障电压信号分解得到的模态分量如图1 所示。可以看出，模态分量中仅有少数模态分量能较好地反映故障状态。考虑到实际信号特征提取往往具有冗余性和高维性，如果计算全部模态分量必然会造成计算维数灾难，因此引入峭度概念对模态分量进行优化筛选。

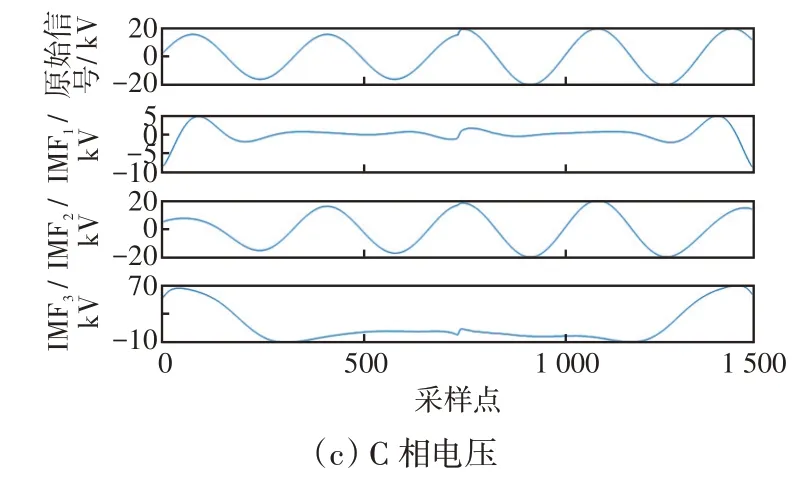
图1 故障暂态电压SVMD 模态分量Fig.1 IMFs of fault transient voltage decomposed by SVMD algorithm

峭度是用于描述概率分布形状的无量纲参数。当信号存在干扰（例如故障）时，信号的峭度是最敏感的特征之一。峭度值越大说明该模态与均值的偏差越大，所包含的故障信息就越丰富，反之，峭度值越小则说明该信号含有的故障信息就越少。信号的峭度计算公式为

式中：η为峭度；E（）为样本期望；x为IMF分量；μ为样本均值；σ为样本方差。

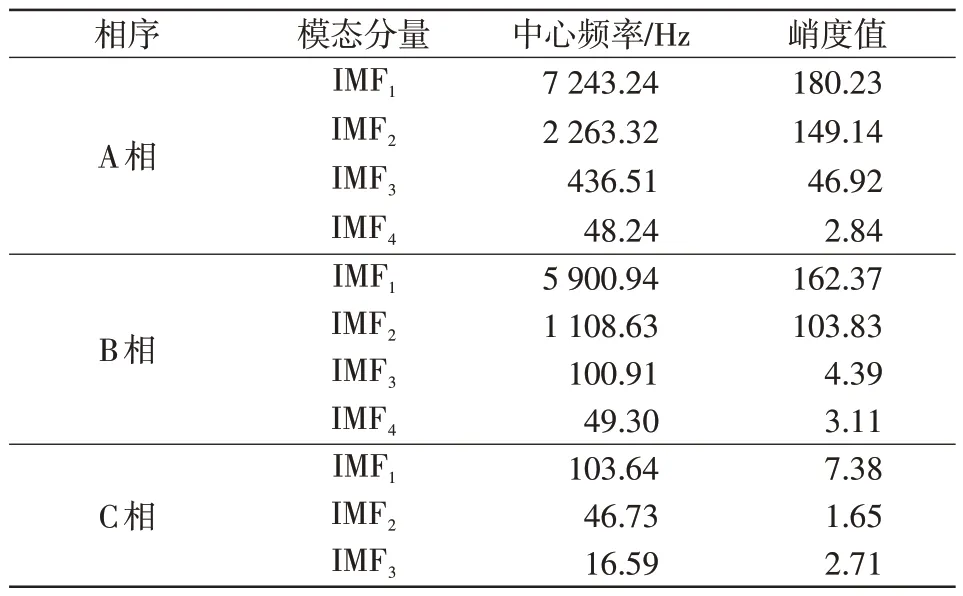
表1 IMF 中心频率及其峭度值Tab.1 Center frequency and kurtosis of IMFs

本文选取峭度值最大的两个模态分量进行信号重构优化，使得优化后的信号包含了大量的故障信息，既实现了计算降维、加快了计算速度，又保留了信号的故障特征。

4 故障识别方法验证及分析

利用PSCAD 仿真实验平台搭建如图2 所示的微电网模型，其中配电网通过公共连接点PCC（point of common coupling）连接微电网，DG1、DG2为采用PQ控制策略的光伏微源和风能微源，DG3为采用U/f控制策略的微型燃气轮机微源并作为主控电源，DG4为光伏电池微源，L1～L4为三相负荷，R1～R5为各分支馈线断路器及测量装备，F1～F3表示发生在微电网内部不同位置的故障。微电网模型的具体参数如表2所示。

表2 微电网模型参数Tab.2 Parameters of microgrid model

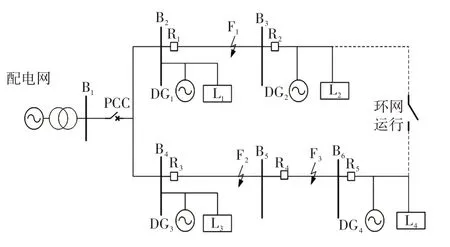
图2 微电网拓扑Fig.2 Microgrid topology

4.1 故障辨别方法验证

根据峭度选取模态分量进行信号重构，并计算重构信号的MPE 值。MPE 取决于信号、延迟时间、尺度因子及嵌入维数。当嵌入维数过小时，MPE对信号中突变的灵敏度就会降低；当嵌入维数过大，MPE 对故障信号细微变化的灵敏度也会降低，同时还会增加计算时间。而延迟时间对于MPE 计算的影响较小，可以忽略不计。经多次实验，在尺度因子λ为10、嵌入维数为5 情况下，本文提取MPE值进行故障特征信息表征。

为验证本文算法，设置F3处发生AB 相接地短路故障，对三相电压进行故障诊断，实验结果如图3所示。

图3 重构信号后MPEFig.3 MPE of reconstructed signal

从图3 可以看出，A 相与B 相电压的MPE 值分别为8.54和8.63，大小相近且都高于0.80；而C相电压的MPE值为6.20，明显小于A相与B相。结果表明，三相电压的MPE 值存在较明显的差异，可以明显区分故障相与非故障相。

由于MPE不受信号幅值的影响，本文所提的故障检测方法在微电网并网时短路电流与微电网离网时相差较大的情况下均适用。图4 为孤岛状态下F1处发生AB两相接地短路故障时在R1处三相电压的MPE值。可以看出，A相与B相电压的MPE值明显大于C相，故障诊断结果与并网状态下保持一致，并未受微电网运行状态的影响。

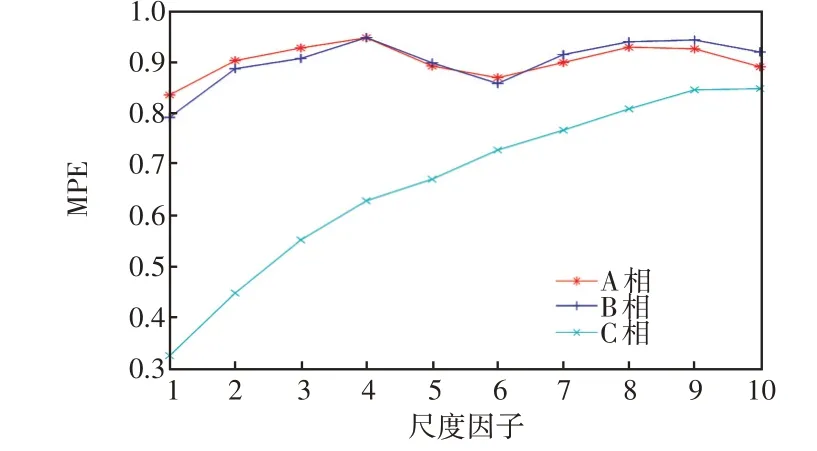
图4 孤岛下两相接地短路故障MPEFig.4 MPE under two-phase grounding fault in islanding mode

对比图3 和图4 可以看出，离网时非故障相与故障相的差异随着尺度因子的增大越来越小，而并网时差异变化较小。这是因为离网时系统电压幅值较小，故障相与非故障相之间的幅值差异没有并网时明显，该差异会随着尺度因子的增加而减少。当尺度因子λ为10 时，离网状态下故障相与非故障相之间的幅值差异很小，但本文方法依然能有效区分故障相与非故障相。

对于不同故障类型、故障地点、故障电阻条件下，每相电压的MPE值如表3所示，其中R1/CG/0.1 Ω/F1表示F1处发生C相接地故障，接地电阻为0.1 Ω，在R1处检测故障信号。从表3可以看出，微电网故障点位置不同或故障电阻不同时，故障相电压的MPE值均明显大于非故障相，并不会影响本文方法检测故障的准确性。

建筑群体的布置是否合理，对冬季获得太阳辐射热和夏季通风降温非常重要。如建筑选址上，建筑用地不宜选择在洼地、山谷等处，应该选择在向阳、避风的地段上，为建筑物争取日照创造必要的条件。结合建筑用地的自然环境、气候条件及建筑物的使用功能等，在不破坏原有生态环境的前提下，结合人的行为活动特点，建立一个自然——人工生态平衡的系统，降低太阳辐射、增强建筑物的通风效果，利用建筑楼群的合理布局，在节约土地资源的前提下增加建筑物之间的间距，既争取日照，又能合理组织气流，从而使建筑物与空气的热交换增加，降低建筑能耗。

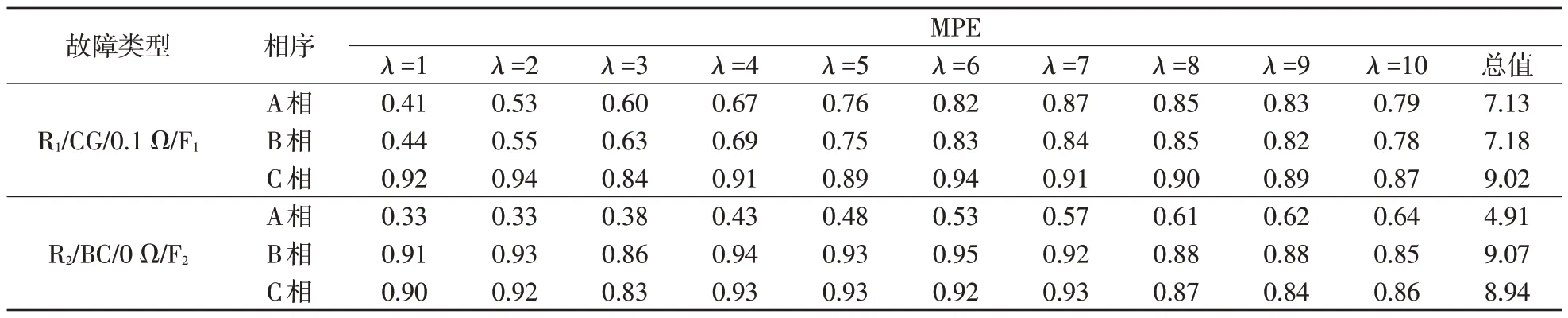
表3 不同故障类型、故障点、故障电阻下的MPE 值Tab.3 MPE in the cases of different fault types, different fault points and different fault resistances

4.2 适用性分析

4.2.1 非故障扰动分析

微电网复杂的运行状态会引起系统内电流出现波动，波动严重时会导致继电保护装置发生保护误动作，造成巡检维修的浪费。为了验证本文方法能有效区分故障与非故障扰动，本文对DG投切、负载投切和DG出力波动3类非故障扰动进行仿真分析，结果如表4所示。

表4 非故障扰动下三相电压的MPE 值Tab.4 Three-phase voltage MPE under non-fault disturbance

由表4 可知，在DG 投切、负载投切及DG 出力波动情况下，本文方法提取出的三相电压的MPE值都小于故障时故障相电压的MPE值，且三相电压的MPE值之间差异很小，MPE总值也明显小于故障时三相电压的MPE总值。对比表3和表4的仿真结果可知，本文方法能有效区分故障与非故障扰动，防止因非故障扰动而引发的保护误动作，提高微电网运行的可靠性与稳定性。

4.2.2 多扰动分析

为了进一步验证本文方法的优越性，在多扰动叠加的情况下进行故障诊断，即微电网发生非故障扰动的同时系统发生故障。

假设微电网在切除负载的同时，F2处发生A相单相接地故障，仿真结果如图5所示。可以看出，A相电压的MPE 值明显大于B 相与C 相，且B 相与C 相电压的MPE 值相似。这表明本文方法在扰动条件下依然能识别故障，具有良好的抗干扰能力。

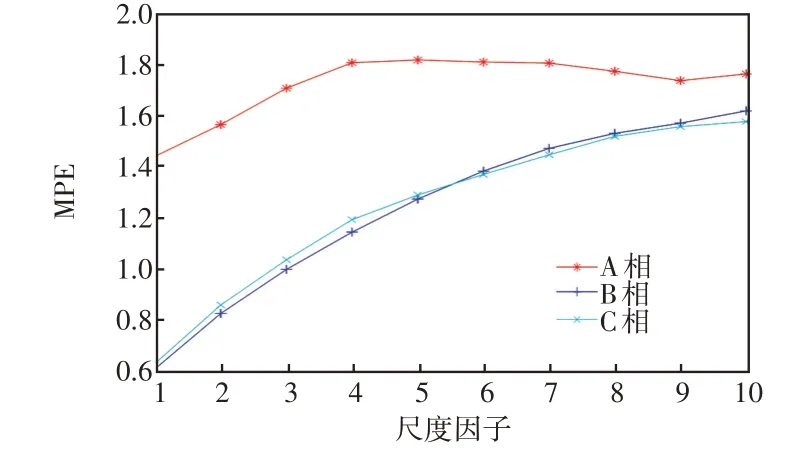
图5 负荷切除同时单相接地故障下MPEFig.5 MPE under single-phase grounding fault while load is removed

4.2.3 高阻接地故障分析

在高阻接地故障情况下，节点的故障电压、电流变化特征不明显，特别在孤岛情况下，受电力电子设备自身保护的影响，故障电气量的幅值会很小。孤岛情况下高阻接地故障时三相电流如图6所示，可以看出，在孤岛情况下，正常时三相电流幅值为13 A，故障时电流最大幅值为16 A，远远小于保护阈值，导致继电保护装置无法正确动作。长时间高阻接地故障运行，必将造成微电网设备损坏。

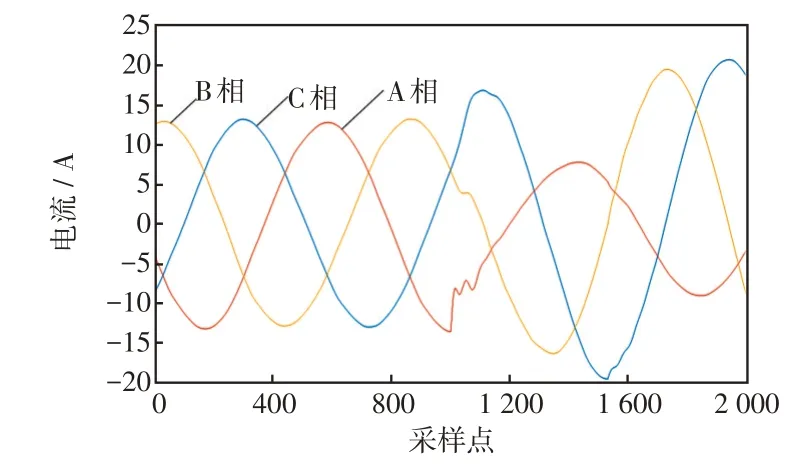
图6 孤岛情况下高阻接地故障时三相电流Fig.6 Three-phase current under high-resistance grounding fault in islanding mode

但本文方法在高阻接地故障下依然能识别出故障特征，对故障进行正确诊断。实验结果如图7所示，可以看出，C 相电压的MPE 值明显大于A 相与B 相电压的MPE 值。这表明本文方法在高阻接地的情况下依然能准确识别系统故障。

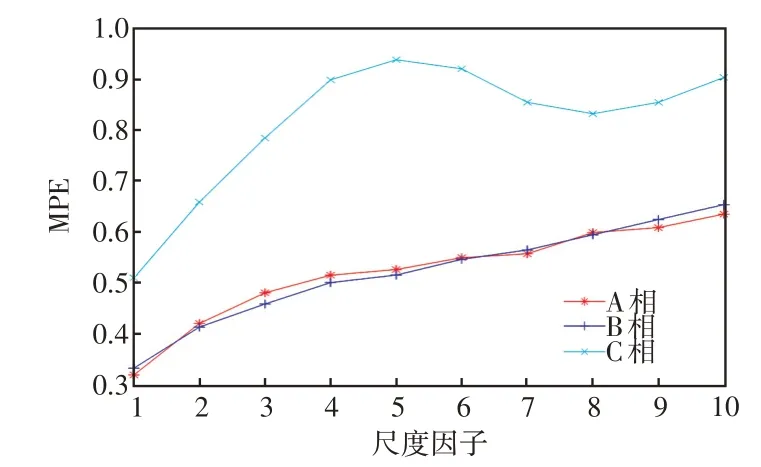
图7 高阻接地下C 相接地故障的MPEFig.7 MPE under phase-C grounding fault with highresistance grounding

本文方法是根据故障相与非故障相的MPE 值差异进行故障识别。由上述分析可知，当发生故障时，故障相电压的MPE 值明显大于非故障相，且故障相电压的MPE 值较大，从而可以判断出故障类型；当发生非故障扰动时，三相电压的MPE 值较小且每相之间的差异也较小，从而可以有效识别出非故障扰动的干扰。同时，本文方法在多扰动及高阻接地故障情况下，都能取得优良的故障识别效果。

5 WOA-KELM 故障诊断

5.1 采用WOA 优化KELM

为了准确区分故障类型，采用KELM 模型对微电网故障类型做进一步分类。由于实际情况下微电网故障特征常常为非线性且故障数据较少，故选取具有较强泛化性的KELM 模型进行故障诊断。KELM 的识别结果受参数C与γ的影响，因此本文利用WOA对KELM参数进行寻优。WOA的初始参数如表5所示。

表5 WOA 初始参数Tab.5 Initial parameters of WOA adopted

5.2 诊断结果分析

本文在PSCAD 平台搭建微电网模型进行故障仿真，从而获得故障数据。对微电网正常运行和故障状态下的电气参数进行数据采集。故障类型设包括单相接地短路、两相接地短路、两相相间短路、三相短路故障；故障电阻分别为0.1 Ω、1.0 Ω、10.0 Ω、20.0 Ω；故障点分别设定在F1、F2和F3处；微电网非故障扰动状态设定为负荷电流波动、微源投切、微源出力波动及双扰动状态；微电网运行模式包括并网运行、离网运行及环网运行。

在获得大量故障仿真实验数据后，选取其中一部分数据作为训练集，对WOA-KELM 故障诊断模型进行训练；剩下数据作为测试集，对WOA-KELM故障诊断模型进行测试。WOA-KELM 故障分类结果如图8所示。

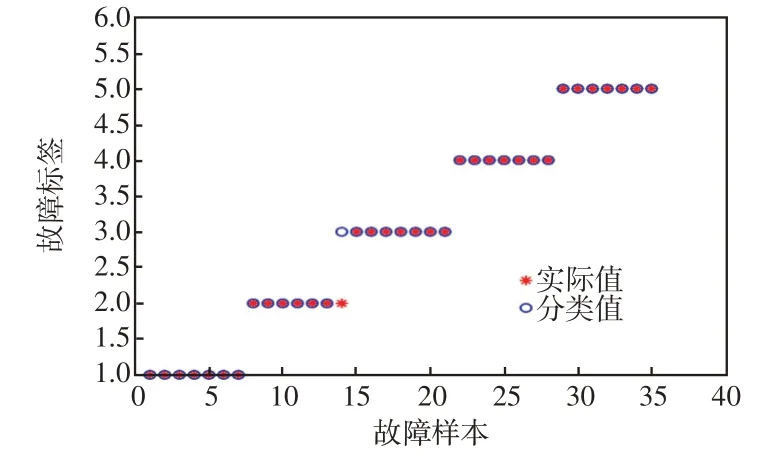
图8 WOA-KELM 故障分类结果Fig.8 Fault classification result obtained using WOAKELM

为了验证本文方法在提取特征及故障识别方面的优势，将本文方法同文献[8]中方法、MPE 与未优化的KELM 结合的方法、单尺度排列熵与WOAKELM 结合的方法进行比较，结果如表6 所示。可以看出，单尺度排列熵与WOA-KELM 结合的方法以单尺度排列熵为特征，其识别准确率远低于以MPE为特征的方法；MPE与未优化的KELM结合的方法以MPE为特征时，识别模型在没有优化的前提下，准确率达到90%，这说明在提取微电网故障特征方面以MPE 为特征具有一定优越性；文献[8]中方法比本文方法的准确率低，这是因为本文方法在高阻接地故障情况下，依然能有效区分故障类别。上述结果表明，本文方法在微电网故障特征提取及故障类型识别上均有一定优越性。

表6 不同诊断方法故障识别结果对比Tab.6 Comparison of fault identification result among different diagnostic methods

6 结 论

本文主要分析了微电网在多扰动故障条件下的故障诊断方法。首先采集故障前后半个周期的信号进行SVMD；然后采用峭度对分解后的信号进行优化重构并计算MPE 值，以构成故障特征信息，将故障特征信息输入至WOA-KELM 模型进行训练；利用训练好的WOA-KLEM 模型进行故障检测。根据实验结果得到主要结论如下。

（1）利用SVMD 算法有效解决了VMD 算法中K值需要事先设定的问题，避免了递归类信号分解方法中存在的模态混叠等问题，为微电网故障特征提取提供了精确的时频信号分量，有效提高了故障识别精度。

（2）采用MPE 表征信号在不同尺度下的故障信息。由于MPE不受幅值大小影响，在不同电压等级下都能有效提取故障特征，具有良好的适用性。本文方法以MPE 为特征，在多扰动、高阻故障及信息缺失情况下依然能保持较好的特征提取能力。

（3）在样本数较少、采样时间短的情况下，所提的WOA-KELM故障诊断模型可以根据据故障特征进行准确快速地故障识别，有效区分故障与非故障扰动，满足微电网故障诊断要求，为故障保护动作提供更加全面的诊断信息。