考虑相位分布特征的多谐波源叠加方法

高 敏，朱明星，汪 清，焦亚东，丁 同

（1. 安徽大学电气工程与自动化学院，合肥 230601；2. 南方电网公司新型智慧城市高品质供电联合实验室（深圳供电局有限公司），深圳 518020）

随着光伏电站、风电场、电气化铁路、高压直流换流站等规模化并网，电力系统的“双高”特征凸显[1]，加剧了电网的波形畸变[2-3]。同时，输配电线路电缆化率的不断提升[4]，电缆对地电容[5-6]和治理装置[7]等引起的谐波谐振问题频现，威胁电力系统的安全稳定运行。因此，加强对非线性负载并网前后的谐波管控是保障电网安全稳定运行的重要手段。然而，并网前预评估过程中的谐波发生量计算，以及并网后测试评估过程中的谐波限值分配，均会涉及多谐波源叠加问题[8]。

目前，多谐波源叠加方法主要有两种实现路径：①通过建立配电网节点模型，模拟在不同节点注入谐波源，采用蒙特卡罗等方法对关注节点的谐波电流叠加结果进行越限概率或畸变水平的统计分析[9-10]，该类方法不关注具体的谐波叠加过程，需建立网络阻抗模型，在实际应用中实施难度较大；②国标《GB/T 14549—1993 电能质量 公用电网谐波》推荐在无相位条件下采用谐波电流叠加方法，并给出了谐波电流叠加公式和谐波电流叠加系数推荐值，为多谐波源叠加的工程应用提供了方法指导。但该标准中叠加系数是在一定的分布假设下得到的[11]，不同类型的非线性负荷谐波电流分布特征均存在差异，采用统一的谐波电流叠加系数会增大谐波电流叠加计算误差[10]，增大谐波管控难度及成本。为获取实际应用场景下谐波电流叠加系数，文献[12]基于核密度估计与重要抽样的蒙特卡罗方法，对两个谐波电流源相位差的余弦值进行期望估算，得到谐波电流叠加系数，进而实现多谐波源叠加的准确计算，但该方法需要对参与叠加的两个谐波源进行同步采样。文献[8]基于多通道同步采样计算多谐波源电流叠加系数的分布，再通过置信区间估计得到谐波电流叠加系数的取值，但该方法也需多通道同步采样。可见，目前关于谐波电流叠加系数的计算主要是基于同步采样和概率统计法解决多随机变量矢量求和问题。在实际应用中，由于测试条件限制，很多场景无法满足同步采样需求。此外，对相位差余弦值的概率分析只能反映两个谐波源的叠加特性，当电网中存在多个不同类型的谐波源时，需对各谐波源的不同组合分别同步采样。

谐波源的相位分布往往表现为在小于2π的扇形分布或椭圆分布[13-15]，通过数据筛选谐波电流较大工况时的相位分布近似呈正态分布[16-18]。为此，本文针对上述谐波源相位角分布特征，提出考虑相位角分布特征参数的谐波电流叠加系数计算方法。该方法通过获取各谐波源相位角分布的期望值和标准差，即可实现任意谐波源之间叠加系数的准确计算，无需同步采样，有利于实际应用。

1 多谐波源叠加模型

多谐波源叠加模型如图1[19-20]所示。其中，为背景h次谐波电压时序数列；ZS,h,t为等效的系统h次谐波阻抗时序数列；为公共连接点PCC（point of common coupling）处h次谐波电压时序数列；为PCC 处h次谐波电流时序数列；，分别为负荷1，2，…，m注入电网的h次谐波电流时序数列；分别为负荷1，2，…，m中h次谐波电流源时序数列；Z1,h,t，Z2,h,t，…，Zm,h,t分别为负荷1，2，…，m的h次谐波阻抗时序数列；h为谐波次数；t为各时序数列的时间维度。

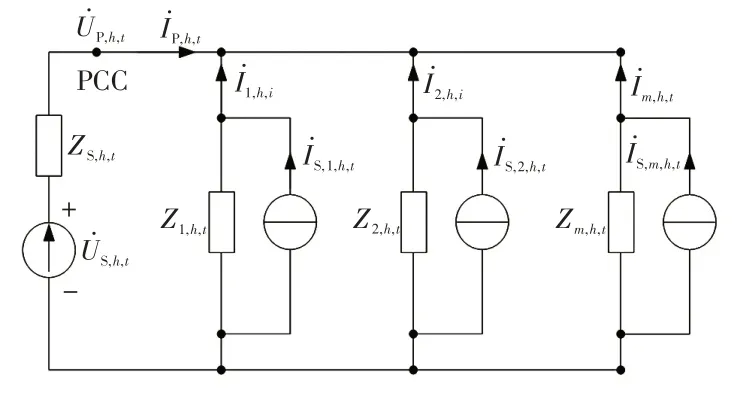
图1 多谐波源叠加模型Fig.1 Multi-harmonic source superposition model

不考虑背景谐波影响时，M个谐波电流源注入PCC形成的总h次谐波电流时序数列可表示为

考虑背景谐波影响下，各谐波源注入PCC处的总h次谐波电流时序数列可表示为

式中，Zh,t为PCC 处所有负荷等效谐波阻抗的时序数列。可见，多谐波源同次谐波电流叠加是指多谐波源谐波相量时序数列的叠加。根据各谐波源谐波电流的幅值和相位变化信息，采用相量时序数列叠加的方式进行叠加计算，如图2所示。

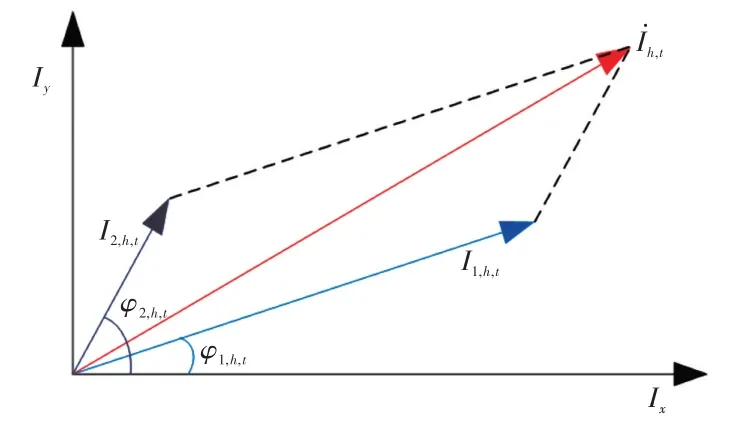
图2 谐波电流相量叠加示意Fig.2 Schematic of superposition of harmonic current phasors

图2中，I1,h,t和I2,h,t为两个独立随机变量的h次谐波电流幅值的时序数列，φ1,h,t和φ2,h,t为两个独立随机变量的h次谐波电流相位的时序数列，则两个时序数列的相量叠加值的幅值计算公式为

对于相互独立的两个随机变量，其乘积的期望值等于期望值的乘积，则对式（3）两边求数学期望可得到谐波电流叠加公式为

式中：Ih、I1,h和I2,h分别为Ih,t、I1,h,t和I2,h,t时序数列的期望值；E() 表示期望运算。当电网中含有多个谐波源时，先将谐波电流含量较大的谐波源进行叠加，再与谐波电流含量较小的谐波源叠加，依此类推。

根据式（4），令谐波电流时序数列的叠加系数Kh为

可见，确定谐波电流叠加系数Kh是多谐波源叠加的关键。在多谐波源系统中，若φ1,h,t和φ2,h,t保持恒定，则谐波电流叠加系数计算结果也是确定的。但在实际应用中，谐波电流相位分布在一定区间内随机变化，而获取φ1,h,t-φ2,h,t的时序数列时，需对两个谐波源开展同步测量，不同时间的测试结果难以兼容，增大了谐波电流叠加系数的计算难度和工作量。因此，如何仅通过获取单个谐波源相位时序数列的分布特征，准确计算不同谐波源的叠加系数，是当前急需解决的技术难题。

2 考虑相位分布特征的谐波叠加方法

2.1 叠加原理及影响因素

根据对典型负荷谐波电流相位分布特征的研究，大多谐波源在谐波电流较大工况下的相位特征近似呈正态分布。正态分布概率密度函数为

式中，μ、σ分别为正态分布的期望值和标准差，μ、σ均为常数且σ> 0 。若随机变量X满足式（6）所示的概率密度函数，则称X服从参数为μ、σ2的正态分布，记作X～N(μ,σ2)。设谐波源1和谐波源2的相位角正态分布参数分别为和，下标1 和2 表示谐波源编号，则相位差φh,t仍呈正态分布，φh,t=φ1,h,t-φ2,h,t，则相位差φh,t满足

根据式（5）和式（7），叠加系数是对两个谐波相位差余弦值的时序数列求期望，若不考虑标准差的影响，即令，则叠加系数可表示为

可见，不考虑标准差影响时，期望值μ1-μ2越小，叠加系数越大，两者呈余弦关系。当期望值一定时，标准差越大，相位角分布的离散性越大，谐波叠加的不确定性越大，则叠加系数越小。因此，当标准差不为0 时，式（8）不成立。为验证标准差对叠加系数的影响，利用蒙特卡罗法产生相位分布满足φ1,h,t～N(30°,(20°)2) 和φ2,h,t～N(5°,(10°)2) 的两组随机数组，如图3（a）和图3（b）所示。将谐波源1与谐波源2 的相位求差值，即φh,t=φ1,h,t-φ2,h,t，得到φh,t的概率密度分布及叠加系数概率密度分布分别如图3（c）和图3（d）所示。

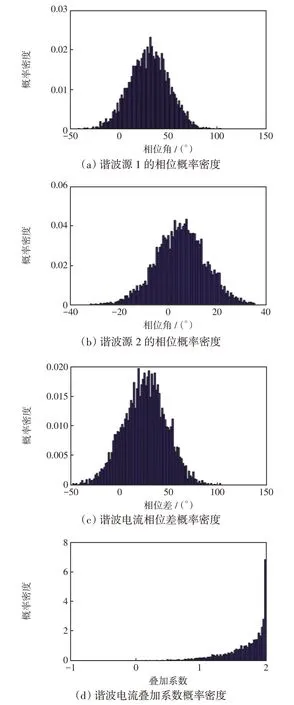
图3 正态分布相量叠加的概率密度Fig.3 Probability density for superposition of normally distributed phasors

谐波源1与谐波源2相位差的期望值为25°，不考虑标准差影响时，叠加系数Kh= 2 cos 25°= 1.81，而根据叠加系数概率密度分布得到的叠加系数为1.68，因此，叠加系数受相位分布标准差的影响也较大。

综上所述，叠加系数取决于谐波源相位分布的期望值和标准差。由于期望值与叠加系数呈余弦关系，因此如何量化标准差对叠加系数的影响是本文方法的关键。

2.2 影响量化分析

为量化分析谐波电流相位分布的标准差对叠加系数的影响，利用蒙特卡罗法，每次生成5 000组满足指定正态分布特征参数的随机数，计算出相位差在不同的数学期望和标准差下叠加系数的变化趋势，如图4 所示。当谐波源相位差的期望值为180°、标准差为0°时，叠加系数为-2，谐波电流叠加时相互削弱。以相位差的期望值等于180°为界限，当相位差的期望值从180°变化至360°，与从180°变化至0°时，两者的叠加系数变化趋势相互对称。当谐波源的相位差为0°（或360°）、标准差为0°时，谐波电流叠加系数为2，谐波电流叠加时可采用线性叠加。

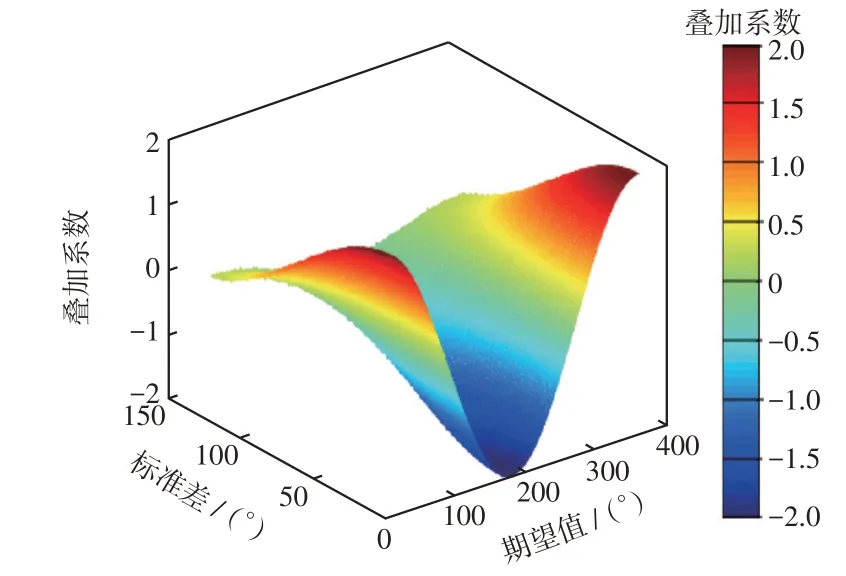
图4 相位分布特征与谐波电流叠加系数的量化关系Fig.4 Quantitative relationship between phase distribution characteristics and Kh

为量化标准差σ对叠加系数的影响，定义谐波电流叠加衰减系数Kσ等于标准差为σ时的谐波电流叠加系数与标准差为0 时的谐波电流叠加系数的比值。在不同期望值下，Kσ随σ的变化趋势如图5（a）所示。可见，在不同期望值下，Kσ与σ的变化趋势均一致，说明Kσ仅受标准差的影响，不受期望值的影响。由图5（a）中各条曲线拟合得到Kσ与σ的对应关系如图5（b）所示。

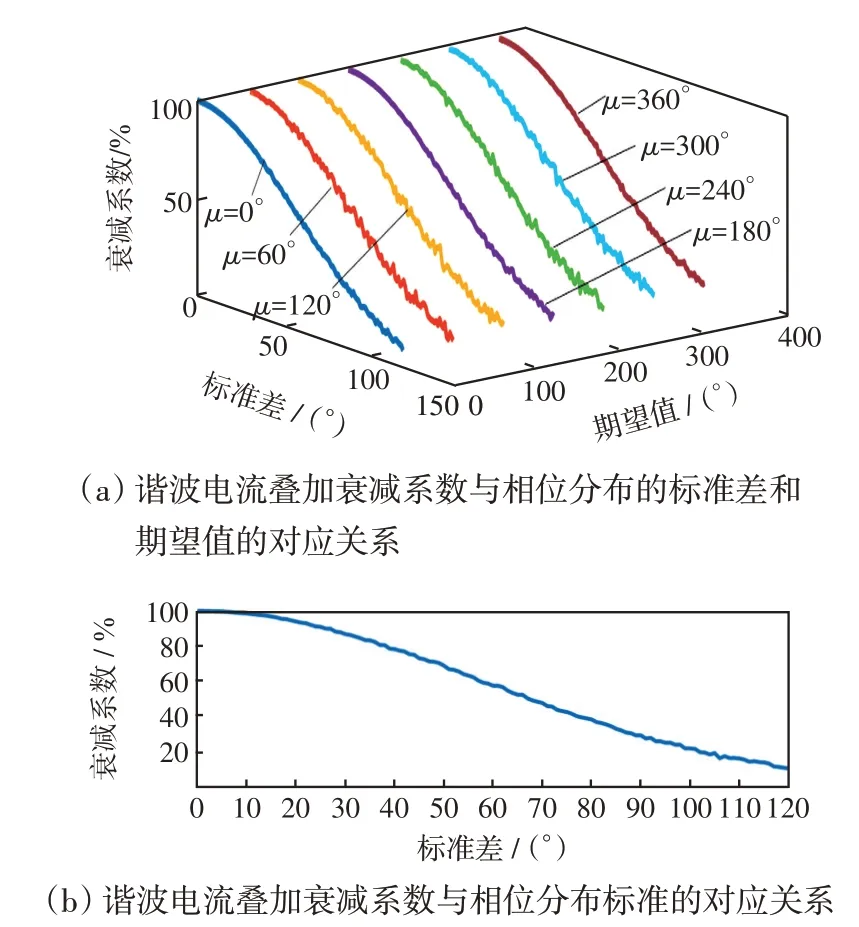
图5 谐波电流叠加衰减系数Kσ拟合结果Fig.5 Fitting results of Kσ

因此，基于蒙特卡罗拟合结果，可得出两个谐波相位呈正态分布的谐波电流叠加系数的计算公式为

这里谐波电流叠加衰减系数Kσ仅与两个谐波源相位差的标准差有关。由式（9）可知，只要获取各谐波源相位角的期望值和标准差，即可准确计算任意谐波源之间的叠加系数。

3 测试数据验证

3.1 居民负荷谐波叠加验证

某居民负荷台区有两条馈出线，为便于对叠加效果进行验证，采用多通道测试仪器对两路馈出线和低压台区总进线的电流信号及供电母线电压信号进行同步采样。以A相3次谐波电流为例，测得馈线1、馈线2的3次谐波电流变化趋势分别如图6（a）和图6（c）所示，两条居民用电负荷馈线的3次谐波电流相位分布特性如图6（b）和图6（d）所示。

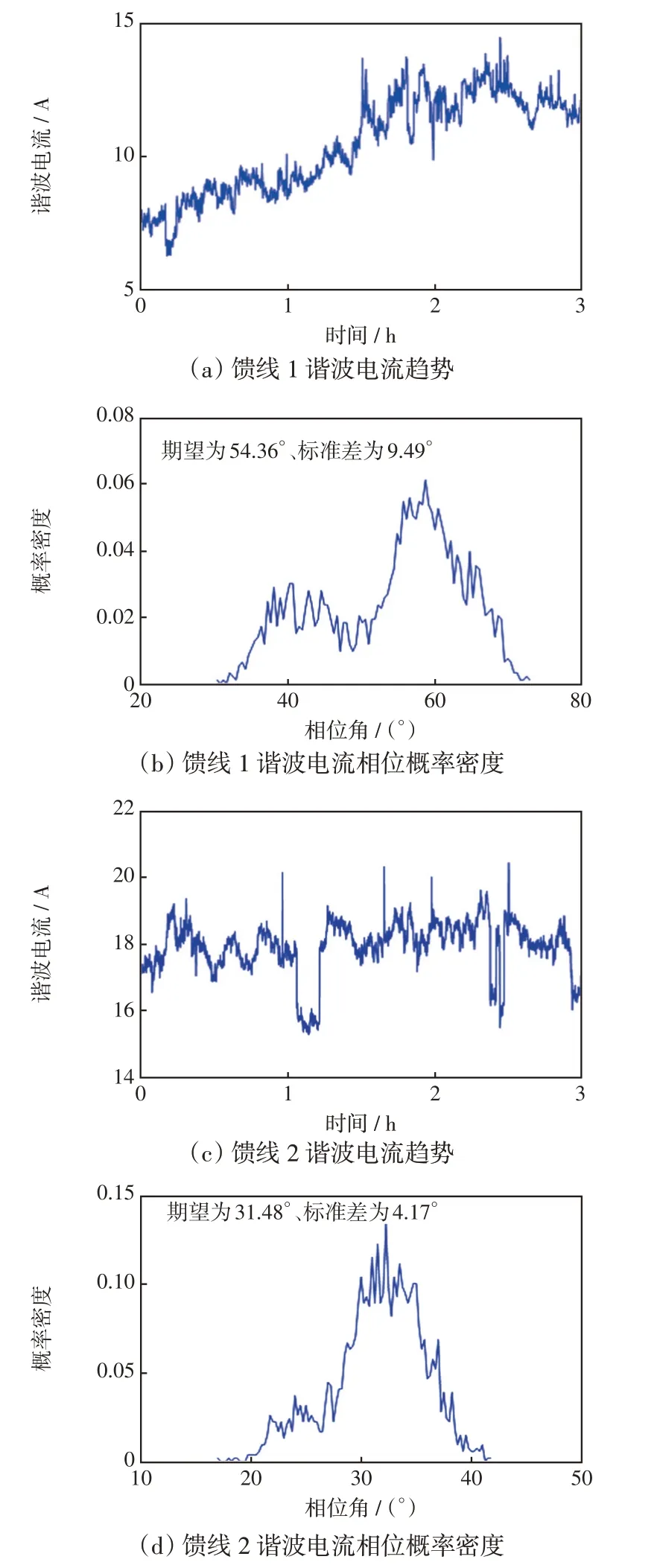
图6 居民用电负荷3 次谐波电流趋势及相位概率密度Fig.6 Trend and phase probability density of 3rd harmonic current of residential electric load

从图6 可以看出，由于居民负荷用电具有随机特征，不同时段的用电设备不同，导致测试时间内的谐波电流相位分布呈现非标准的正态分布。但是，根据两条居民负荷馈线3次谐波电流相位差的正态分布特征参数，馈线1 的3 次谐波电流相位角分布的数学期望和标准差分别为54.36°和9.49°，馈线2的3次谐波电流相位角分布的数学期望和标准差分别为31.48°和4.17°。两者相位差分布的数学期望μ= 54.36°- 31.48°= 22.88° ，相位差分布的标准差。根据图5得到标准差σ= 10.37° 对应的谐波电流叠加衰减系数Kσ= 0.98 ，根据式（9）计算出的谐波电流叠加系数期望值为Kh= 2 cos 22.8°× 0.98 = 1.805 8 。

根据本文方法计算得到的谐波电流叠加系数和国标《GB/T 14549—1993 电能质量 公用电网谐波》中提供的3次谐波电流叠加系数（即1.62），分别计算两条居民负荷馈线的谐波电流叠加值，并与实测的居民负荷总进线3次谐波电流进行对比，结果如图7 所示。可见，实测的居民负荷总进线3 次谐波电流最大值、95%概率值和平均值分别为31.80 A、30.81 A 和27.63 A；而根据国标推荐的叠加方法计算的居民负荷总进线3次谐波电流最大值、95%概率值和平均值分别为31.42 A、29.94 A和27.03 A；本文方法计算的居民负荷总进线3次谐波电流最大值、95%概率值和平均值分别为32.19 A、30.66 A 和27.66 A。以95%概率值进行评估时，国标推荐的叠加方法和本文方法的计算误差分别为2.8%和0.5%，本文方法计算误差降低了82.1%，与国标要求的A级谐波测量仪允许误差（≤5%）相比，本文方法计算误差降低显著。

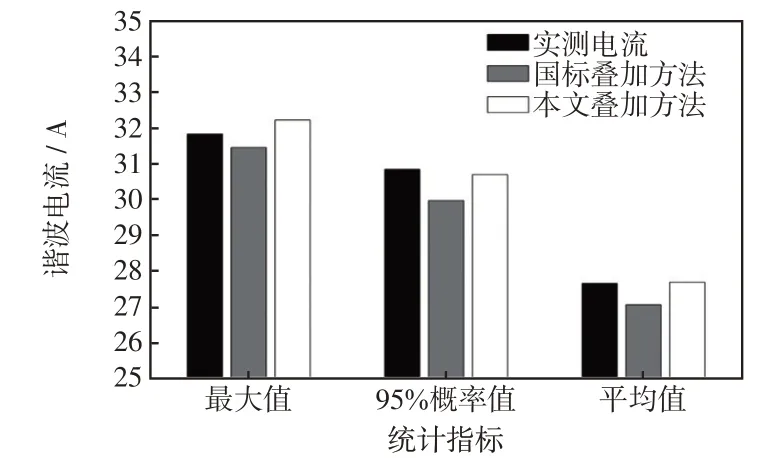
图7 不同方法叠加结果与实际测试结果对比Fig.7 Comparison between superimposed results calculated bydifferent methods and actual test results

3.2 充电站负荷谐波叠加验证

某充电桩负荷含两条充电桩馈线，每条馈线有两个直流充电桩，为便于对叠加效果进行验证，采用多通道测试仪器对两条充电桩馈线和总进线的电流信号及供电母线电压信号进行同步采样。以A相的5次谐波电流为例，测得馈线1、馈线2的5次谐波电流变化趋势分别如图8（a）和图8（c）所示。充电桩存在明显的运行周期，充电时段的谐波电流变化相对稳定，非工作时段的谐波电流含量很小。为排除充电桩非工作时段谐波电流相位分布对叠加系数计算结果的影响，通过数据筛选剔除充电桩非工作时段的谐波数据，数据筛选阈值为对应馈线最大谐波电流的0.3倍。数据筛选后两条充电桩负荷馈线的5 次谐波电流相位分布特性的分析结果如图8（b）和图8（d）所示。

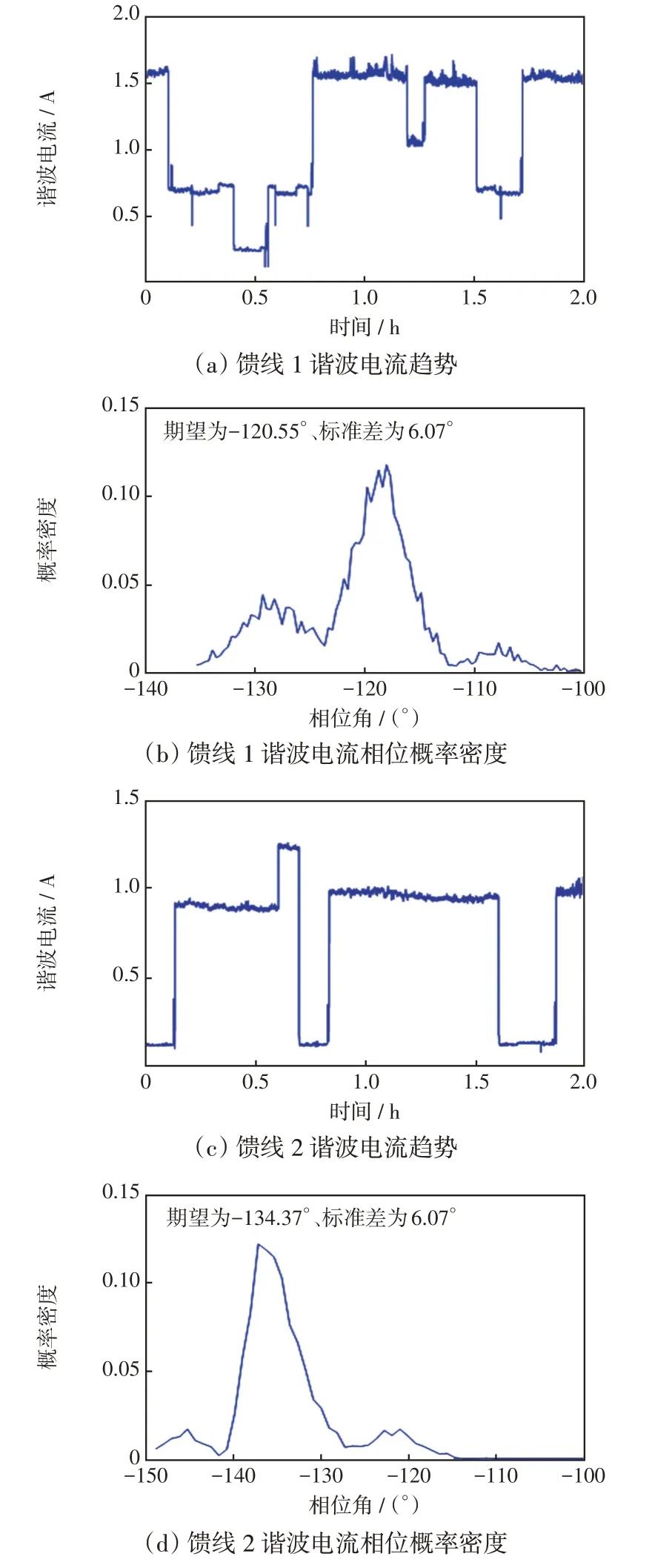
图8 充电桩5 次谐波电流趋势及相位概率密度Fig.8 Trend and phase probability density of 5th harmonic current of charging pile

从图8 可以看出，对于充电桩负荷来说，充电过程中谐波电流相位稳定，相位分布近似呈正态分布。而根据两条充电桩馈线5 次谐波电流相位差的正态分布特征参数，馈线1 的5 次谐波电流相位角分布的数学期望和标准差分别为-120.55°和6.07°，馈线2 的5 次谐波电流相位角分布的数学期望和标准差分别为-134.37°和6.07°，则两者相位差分布的数学期望μ= 13.82° 、标准差σ= 8.58° 。根据图5 可得到标准差σ= 8.58° 对应的谐波电流叠加衰减系数Kσ= 0.985 ，谐波电流叠加系数期望值Kh= 2 cos 13.82°× 0.985 = 1.913 。

根据本文方法计算的谐波电流叠加系数和国标中提供的5次谐波电流叠加系数（即1.28）分别计算两条充电桩馈线的谐波电流叠加值，并与实测的两条充电桩总进线5次谐波电流进行对比，结果如图9所示。可以看出，实测的两条充电桩总进线的5次谐波电流最大值、95%概率值和平均值分别为2.670 A、2.529 A 和1.822 A，而根据国标推荐的叠加方法计算的两条充电桩总进线的5次谐波电流最大值、95%概率值和平均值分别为2.461 A、2.326 A和1.710 A，本文方法计算的两条充电桩总进线的5 次谐波电流最大值、95%概率值和平均值分别为2.669 A、2.528 A和1.837 A。以95%概率值进行评估时，国标推荐的叠加方法和本文方法的计算误差分别为8.03%和0.04%，本文方法的计算误差降低了99.50%。

图9 不同方法叠加结果与实际测试结果对比Fig.9 Comparison between superimposed results calculated by different methods and actual test result

4 结 论

本文提出了一种考虑谐波电流相位分布特征的多谐波源叠加方法，主要结论如下。

（1）谐波叠加是相量运算，在实际电网中由于谐波的幅值和相位均在一定区间内随机变化，因此多谐波源叠加的本质是随机矢量求和问题。

（2）叠加系数取决于谐波电流相位分布的数学期望和标准差。本文基于蒙特卡罗法量化了标准差对谐波电流叠加系数的影响，提出了基于数学期望和标准差的谐波电流叠加系数计算公式。通过在居民负荷和充电桩负荷两种典型场景中的应用验证，本文方法较国标推荐方法的计算误差降低80%以上。

（3）实际应用中往往以谐波的95%概率值进行评估，当非线性负荷的谐波电流变化幅值较大时，筛选出谐波电流较大时刻的谐波电流相位分布特征进行计算，可以显著降低计算误差。

（4）本文方法以基波电压上升沿过零点为谐波电流相位计算的参考基准，仅需计算或获取各谐波源的相位分布特征参数，即可实现任意谐波源的叠加计算，具有计算量较小、计算误差小、无需同步测量等优点，提高了多谐波源叠加的准确性和工程实用性。

本文方法在各谐波源相位角近似满足正态分布的场景下取得了较好的叠加效果，但对于交流电弧炉等电弧类非线性负荷场景下，谐波电流相位角不满足正态分布时，谐波电流叠加方法的适用性及改进是下一步需重点研究的方向。