InSCC拓扑结构的能控性分析

肖朋朋,纪志坚,刘允刚,林 崇

(1.青岛大学自动化学院,山东 青岛 266071;2.山东省工业控制重点实验室,山东 青岛 266071;3.山东大学控制科学与工程学院,济南 250061 )

0 引言

随着计算机技术的发展,以分布式网络化系统为代表的新型系统模式,在实际应用中充分体现了相对于单个系统更加方便和智能的优势,多智能体系统越来越受到人们的关注。不仅在控制领域,在无人机编队等领域[1-5]也对多智能体系统进行了研究。

众所周知,要实现对一个系统的控制,前提是保证系统的能控性。能控性概念是20世纪60年代由卡尔曼[6-7]首次提出,2004年[8]能控性的概念被引入到多智能体的研究中,文章利用领导者-跟随者框架定义了系统的能控性。近些年对多智能体系统能控性[9-11]和能观性的研究逐渐增多,在She等[12]的文章中利用拓扑特征来研究有符号路图和循环图领导者的选择,以确保领导者-跟随者的能控性。在Guan等[13]的文章中研究了用有向加权符号图表示有符号网络的多智能体系统的能控性。Sun等[14]研究了一类符号多智能体网络的能控性,在广义等价划分的基础上,提出了能控子空间上界的图论刻画。在Tian等[15]的文章中研究了切换系统的等价划分定义及应用。在Zhao等[16]的文章中研究了异构多智能体系统的能控性。在Liu等[17]的文章中研究了离散时间多智能体系统的能观性问题。

对多智能体系统的研究大多是从代数和图论角度出发的,其中从图论角度得到的结论,在使用时仅依靠网络结构就可以描述系统的能控性,这极大减少了计算量,在实际应用中具有重要意义。之前的工作揭示了对称性、自同构和等价划分等结构对能控性的影响,但这类结构并不能包含所有情况,还需要挖掘新的特殊结构,并分析其对能控性的影响。本文提出一种新的拓扑结构输入强连通分量(InSCC),用于解决含有输入强连通分量的一类多智能体系统的能控性问题。

本文的贡献主要包含4个方面:1)提出了InSCC结构,利用PBH判据等工具,分析了含有InSCC结构的网络拓扑的能控性,相应地给出了保证系统能控的领导者选择方法;2)以InSCC结构为基础,在不同的InSCC结构之间及路图中增加通讯边,证明了按本文提出的方式增加通讯边并不改变多智能体系统的能控性,这为通过加边的方式构造更为一般的能控图提供了一种可尝试的方法;3)依据InSCC结构的特性,提供了一类能控拓扑的构造方法;4)给出了含有InSCC结构的多智能体系统在切换拓扑下能控的充要条件。

1 预备知识

图论知识:一个由n个节点构成的有向拓扑图G(V,E,A),图的点集用V={v1,v2,…,vn}表示,图的边集用E={(vi,vj)|vi,vj∈V,i≠j}表示,A=[aij]∈Rn×n表示加权邻接矩阵,aij表示顶点j到顶点i的权重,若无特殊说明,aij=1。本文不考虑存在自环的情况,即不存在(vi,vi)∈E。Ni={j∈V∣(j,i)∈E}表示节点i的邻居集合。如果在每一对不同的顶点i,j之间都有一条从i开始到j结束的定向路径,那么图G就是一个强连通图。对于一个集合U,|U|代表集合中元素的个数,对于有向图G,di=|Ni|表示节点i的度,有向图G的度矩阵用D(G)=diag(d1,d2,…,dn)表示。拉普拉斯矩阵是相较于度矩阵的另一种表达图中顶点关系的矩阵,拉普拉斯矩阵用L(G)=D(G)-A(G)表示。

数学符号:R表示实数集,Rn为n维实向量空间。X/Y表示属于X但不属于Y的集合,I为单位矩阵,0表示文中合适维度的零矩阵,φ表示空集。

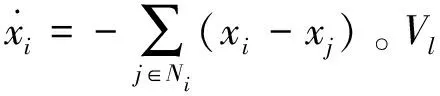
(1)

其中,L∈Rn×n是拉普拉斯矩阵,B∈Rn是控制输入矩阵。

定义1对于一个加权有向图G(V,E,A),当且仅当G1=(V1,E1,A1)满足1)V1⊆V,2)E1⊆E,3)A1是A的子矩阵时,称G1是G的一个子图。

定义2对于有向图G的一个子图G′,如果G′为单向强连通环图,且对于任意j∈V/V′,i∈V′,都有(i,j)∉E,强连通子图G′整体只有单个输入,这种结构称为InSCC。含有节点数目不同的InSCC结构称为不同的InSCC。在本文中把没有入度的节点作为初始节点,即节点1为初始节点,如图1 所示。

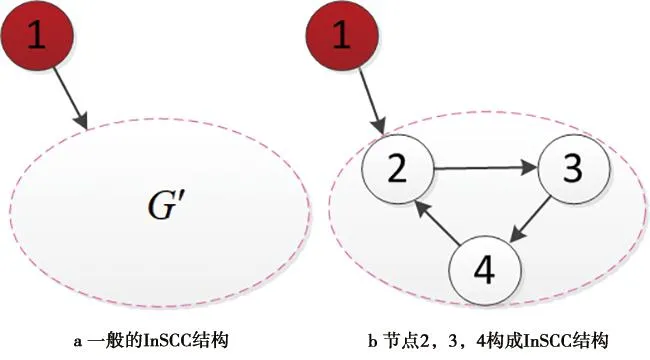
图1 InSCC结构

2 含有不同InSCC结构的多智能体系统的能控性分析

在目前为止的所有文献中,关于能控图构造的文献很少,大部分都是非能控图,本节为构造能控图提供了图论基础。分析只含有不同InSCC结构的多智能体系统的能控性,以及含有InSCC结构和路图的多智能体系统的能控性,给出领导者的选择方法以实现系统能控。对于一个有向拓扑图G,如果含有相同InSCC结构,则存在对称节点[18],此时网络不能控,故不探究。本文着重分析含有不同InSCC结构的多智能体系统的能控性。

2.1 单领导者时仅含有InSCC的多智能体系统的能控性分析

本节讨论含有不同InSCC结构的多智能体系统的能控性,如图2所示。

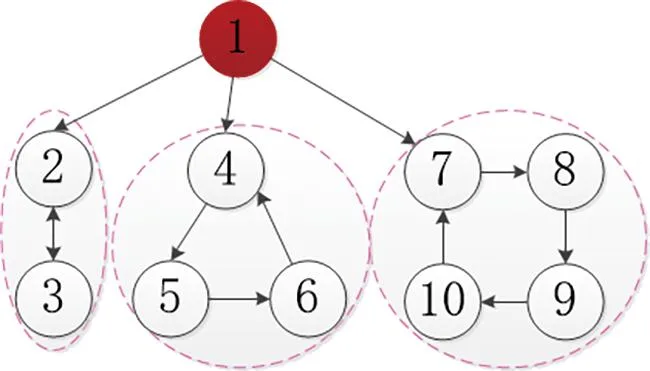
图2 仅含有InSCC结构的有向拓扑

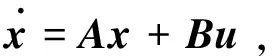
命题1在含有不同InSCC的多智能体系统中,当选择初始节点为领导者时,多智能体系统是能控的。

证明:不失一般性,假设多智能体系统含有m个InSCC结构,则系统的拉普拉斯矩阵为

(2)

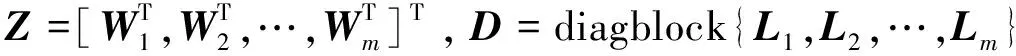
(3)

为了进一步体现有向图与无向图的区别,考虑图2所对应的无向图(见图3)。当选择初始节点1为领导者时,经验证得到无向图的能控子空间维数为8,而有向图的能控子空间维数为10,对于本文考虑的情况,有向图的表现在一定程度上更为出色,这里面的区别是值得研究的。注意到,基于无向图等价划分[20]的定义,在图3中存在2对自同构节点,因此选择初始节点1为领导者时,能控子空间的维数就等于节点数n和等价划分胞腔数之差。因此相较于无向图,本文利用有向图去构造能控图是有优势的。

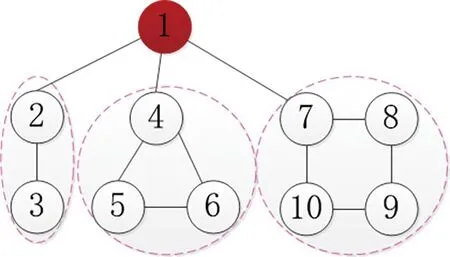
图3 与仅含有InSCC的有向拓扑所对应的无向拓扑

2.2 多领导者时仅含有InSCC的多智能体系统的能控性分析

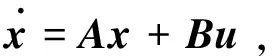
命题2在含有InSCC结构的多智能体系统中,选择初始节点和第k个InSCC结构中的部分节点为领导者,且控制输入矩阵为单列矩阵,第k(k=1,2,…,m)个InSCC结构中领导者数量严格小于其节点的数量时,多智能体系统是能控的。

2.3 含有InSCC和路图的多智能体系统能控性分析

在本文2.1和2.2小节中,给出了领导者的选择方法以实现系统能控。为了使结论更加一般化,在只含有InSCC结构的多智能体系统中引入路图,将路图的端节点与初始节点相连接,如图4所示。

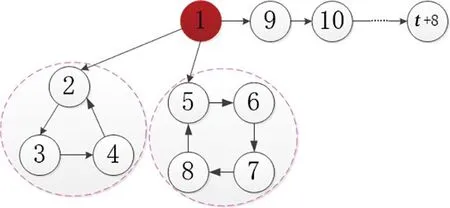
图4 含有InSCC和单条路的多智能体系统

命题3在一个含有不同InSCC结构和单条路的多智能体系统中,选择初始节点为领导者,那么它对应的多智能体系统是能控的。

证明:假设多智能体系统中共有n+t个节点,包含m个不同的InSCC和1条含有t个节点的路图,系统的拉普拉斯矩阵L1为

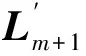
当选择初始节点为领导者时,输入矩阵B1=[1,0,…,0]T,B1∈Rn+t,

所以,rank[λI-L1|B1]=n+t,由引理1可得选择初始节点为领导者时,多智能体系统是能控的。

3 含有不同InSCC结构的拓扑加边后的能控性分析

在第2节中讨论了含有InSCC结构和路图的一类拓扑的能控性问题,给出了领导者的选择方法以实现系统能控。从中可以看出,除了共同接收初始节点的信息,InSCC结构之间没有通讯,是一个比较理想的假设。实际上对于更一般的图,不同InSCC结构之间往往存在耦合关系。本文首先在仅含有InSCC结构的拓扑图中,InSCC结构之间加单向边,其中每个InSCC结构中都有偶数个节点。其次,讨论在InSCC结构之间加单向边,同时在路图中增加逆向边,得到了不影响系统能控性的加边方法。

3.1 含有InSCC结构的多智能体系统加边后的能控性分析

在不同InSCC结构之间加单向边,如图5所示。

图5 增加正单向边后的拓扑

定义3对于只含有不同InSCC结构的多智能体系统,把不同的InSCC结构看作不同的胞腔,不同胞腔之间仅内部节点数量存在差异,且不存在两个相同的胞腔。两个不同的胞腔Ci,Cj之间增加由Ci指向Cj的通讯边,其中Ci中的节点数量小于Cj中的节点数量,增加的这种边称为正单向边,反之为负单向边,正单向边和负单向边构成的集合分别为P+,N-。

定理1在只含有不同InSCC的多智能体系统中,增加正单向边后,当选择初始节点为领导者时,多智能体系统是能控的,加边前后两种系统的能控性相同。

同理,增加负单向边也不改变多智能体系统的能控性,这为构造更复杂的能控图提供了加边的方法。

3.2 含有InSCC结构和单条路图的多智能体系统加边后的能控性分析

在2.3小节中,分析了InSCC结构和路图共同组成的拓扑结构的能控性,给出了领导者的选择方法以实现系统能控。根据定理1的分析,在不同InSCC结构之间加单向边不改变多智能体系统的能控性,同样能够实现单领导者能控。本节考虑在不同InSCC结构之间加单向边,同时在路图上增加逆向边,路图中增加的逆向边是从节点vj指向节点vi,i,j∈{n+1,n+2,…,n+t}且j>i,如图6所示。

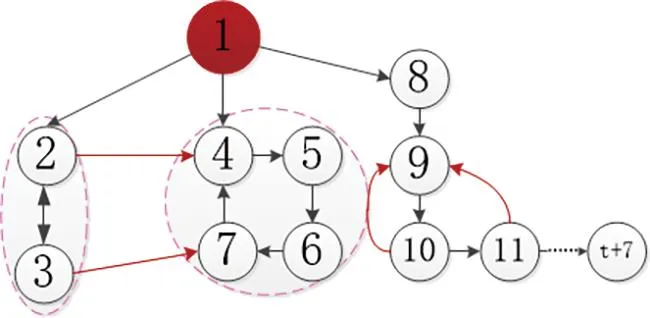
图6 InSCC增加正单向边和路图增加逆向边的拓扑

定理2在只含有不同InSCC结构和路图的拓扑中,在不同InSCC结构之间加正单向边,同时在路图上增加逆向边,当选择初始节点为领导者时,加通讯边前后能控性相同。若含有InSCC结构和单条路图加边后的多智能体系统是能控的,则在领导者的选择中必然有初始节点。

证明:在不同InSCC结构之间加正单向边的同时在路图上增加逆向边,对应的拉普拉斯矩阵L3为

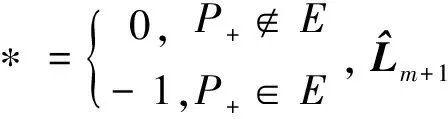
4 一类能控图的构造

本节主要利用InSCC结构和有向路图的特点,提供一类能控图的构造方法。

本文对含有不同InSCC结构的多智能体系统的能控性做了分析,发现了InSCC结构和路图所具有的特殊性质。在目前的众多文献中,很少有能控图构造的结论。本文利用InSCC结构和路图的特性来构造一类能控图。

方法1:如图7a所示的拓扑图,在命题1的基础上,加入一个含有t个节点的有向路图,路图的末端节点与初始节点相连接,当选择端节点1为领导者时,多智能体系统是能控的。

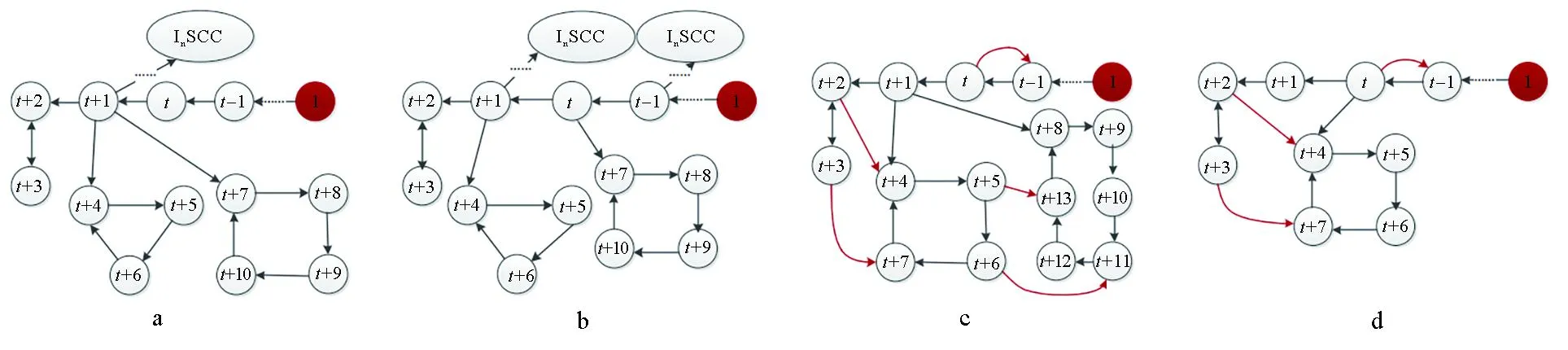
图7 构造的含有InSCC结构和路图的能控拓扑

方法2:如图7b所示的拓扑图,利用不同InSCC结构的特性,在一条含有t个节点的路图基础上,从每个节点引出不同的InSCC结构所构成的复杂拓扑,当选择端节点1为领导者时,系统是能控的。

方法3:如图7c所示的拓扑图,每个InSCC结构都由偶数个节点组成,在定理1的基础上,加入一个含有t个节点的有向路图,路图的末端节点与初始节点相连,并且在有向路图上增加逆向边,当选择端节点1为领导者时,多智能体系统是能控的。

方法4:如图7d所示的拓扑图,每个InSCC结构都由偶数个节点组成,利用不同InSCC结构加单向边和有向路图加逆向边不改变能控性的特性。在一条含有t个节点的有向路图上,从每个节点引出不同的InSCC结构所构成的复杂拓扑,同时不同的InSCC结构之间增加单向边,有向路图增加逆向边。当选择端节点1为领导者时,多智能体系统是能控的。

这些结论的证明可以参考本文前边结论的推导。我们讨论了固定拓扑下含有InSCC结构的多智能体系统的能控性,根据InSCC结构的特点,给出了几种能控图的构造方法。但在现实生活中,各种情况错综复杂,固定拓扑下的多智能体系统往往不能解决很多实际问题,多智能体系统可能是时变的。

5 含有InSCC结构的多智能体系统在切换拓扑下的能控性分析

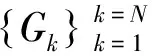
(4)

其中,Lσ(t)∈Rn×n为Gσ(t)的拉普拉斯矩阵,系统(4)包含N个子系统(-Lk,Bk),k=1,2,…,N,σ(t)=i表示子系统(-Li,Bi)在t时刻被激活。

定义4如果对于任意初始状态x0,任意终端状态xf,存在切换信号σ(t)和分段连续输入函数u(t),t∈[t0,tT],可以使系统从x(t0)=x0驱动到x(tT)=xf,此时系统(4)是能控的。

引理3[21]当且仅当rank(Qs(-Li,Bi))=n时,多智能体系统(4)是能控的,其中

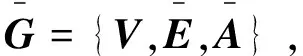
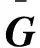
(5)

在矩阵(5)中,从2N列到2N+1列之间加入块列-L2B1,…,-LNB1,…,-LNBN,再从矩阵(5)的最后增加块列(-L2)(-L1)n-2B1,…,(-LN)n-1B1,…,(-LN)n-1BN,得到如式(6)的矩阵

[B1,B2,…,BN,-L1B1+…+(-LN)B1,…,-L1BN+…+(-LN)BN,

-L2B1,-L3B1,…,-LNB1,…,-LNBN,…,(-L1)n-1B1+…+(-LN)n-1B1,…,

(-L1)n-1BN+…+(-LN)n-1BN,(-L2)(-L1)n-2B1,…,(-LN)n-1B1,…,(-LN)n-1BN]

(6)

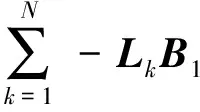
[B1,B2,…,BN,-L1B1,…,-LNB1,…,-LNBN,…,

(-L1)n-1B1,…,(-LN)n-1B1,…,(-LN)n-1BN]

(7)

式(7)为行满秩矩阵,通过引理3可以得到只含有InSCC结构在切换拓扑下的系统(4)是能控的。

(必要性)假设系统(4)是能控的,即能控性矩阵C行满秩,其中

本文命题1证明在固定拓扑下含有InSCC结构的多智能体系统,当选择初始节点为领导者时,多智能体系统是能控的。因此在Gk={V,Ek,Ak}中,当选择初始节点为领导者时,子网络均是能控的。在矩阵C中去掉块列-L2B1,…,-LNB1,…,-LNBN和(-L2)(-L1)n-2B1,…,(-LN)n-1B1,…,(-LN)n-1BN,得到

(8)

矩阵(8)仍然有n个线性无关的列向量,所以矩阵(8)是行满秩的。由于列初等变换不改变矩阵的秩,因此我们用向量-L1B1加上-L2B1-…-LNB1,-L1BN加上-L2BN-…-LNBN,(-L1)n-1B1加上(-L2)(-L1)n-2B1+…+(-LN)n-1B1,(-L1)n-1BN加上(-L2)(-L1)n-2BN+…+(-LN)n-1BN,得到

[B1,B2,…,BN,-L1B1+…+(-LN)B1,…,-L1BN+…+(-LN)BN,…,

(-L1)n-1B1+…+(-LN)n-1B1,…,(-L1)n-1BN+…+(-LN)n-1BN]

(9)

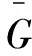
6 数值验证

例:在图5所示的有向拓扑中,节点2、3和节点4、5、6、7,以及节点8、9、10、11、12、13分别组成了3个不同的InSCC结构,选择在不同的InSCC结构之间增加单向边,如图5所示,增加的通讯边已用红色作为区分,在节点2和节点4、节点3和节点7、节点5和节点13、节点6和节点11之间分别加一条正单向边。下面将用具体实例来验证本文的结论,当选择初始节点1为领导者时

根据引理1得rank[sI-L2|B2]=13,在一个含有InSCC结构的多智能体系统中,当选择初始节点为领导者时,多智能体系统是能控的,加边并不影响多智能体系统的能控性,这与定理1完全一致。

7 结论

本文对一类含有InSCC结构的多智能体系统的能控性进行了研究,结果表明:对于仅包含InSCC结构的多智能体系统,选择初始节点为领导者时系统是能控的;对于包含InSCC结构和路图结构的多智能体系统,也得到了相应的结论,给出了领导者的选择方法以实现系统能控。受此启发,提出了不改变系统能控性的通讯边增加规则及一类能控拓扑的构造方法。最后基于得到的结果,对切换拓扑条件下相关系统的能控性进行了讨论,得到了含有InSCC结构的多智能体系统在切换拓扑下能控的充要条件。本文得到的结果为研究更为复杂的多智能体系统的能控性提供了一定的理论参考,未来工作中将进一步探索InSCC结构在寻找本质能控图(在任意领导者选择下均可控的网络)方面的潜在作用。