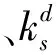基于熵的多属性决策超网络重要节点识别方法

吴英晗,李明达,胡 枫

(青海师范大学 a.藏语智能信息处理及应用国家重点实验室;b.高原科学与可持续发展研究院,西宁 810008)

0 引言

近年科技的高速发展,使人类社会处于信息化数据时代。从现实社会的关系网到虚拟的互联网,从线上到线下,我们的生活始终与复杂网络息息相关[1]。比如与生活密切相关的因特网、交通网络、电力网络[2];与他人交流的社交网络、科研合作网络[3];可以说网络无处不在。随着对网络科学领域的深入研究,人们发现基于超图的超网络[4-6]可以更好地表述公交网络中线路途径多个站点以及科研合作网络中多个作者多次合作等真实网络的情况,于是人们便将研究的焦点转向更能精准刻画真实网络多元复杂关系的超网络。无论是基于普通图的复杂网络[7-9]还是基于超图的超网络,都存在部分节点,其失效会对整个网络的结构及功能产生深层次的影响[10],因此,如何度量超网络中节点的重要性以及挖掘超网络中的重要节点仍旧是网络科学领域值得研究的问题。

目前,诸多学者根据实际需求针对节点重要性问题做了相关研究。Estrada等[5]将复杂网络中的子图中心性和聚类系数指标扩展到超网络,并用这两种指标识别出了3类现实超网络中的重要节点;Kapoor等[11]将节点度中心性的概念推广到社交超网络,依据节点的强度将节点间的联系分为强联系和弱联系,并以此为附加特征,从而提高了预测的准确性。王雨等[12]从超网络视角出发,综合考虑作者自身科研价值以及作者间的重要性贡献值,提出了一种新的重要度评价指标D′,有效识别出了科研领域的核心作者。Song等[13]基于转录组学数据构建超图,引入新的平均超图中心性指标对与病毒/病原体感染相关的基因集进行对比分析,结果表明平均调和s-介数中心性能够有效识别关键基因。周丽娜等[14]将复杂网络中的K-shell分解法扩展到超网络,基于复合参数的思想,结合超度及K-shell值利用欧氏距离公式提出了一种超网络关键节点识别指标。

1 相关工作

1.1 超网络相关概念

1.2 超网络中节点重要性评价相关指标

定义1超网络介数中心性 介数中心性[18]用于刻画节点对网络中沿着最短超路径传输网络流的控制力,可表征网络中处在“桥”位置节点的重要性。节点vi的介数中心性定义为

(1)

其中,gk为节点vj和节点vk之间的最短超路径数目,gk(i)为节点vj和节点vk之间的最短超路径中经过节点vi的数目。

定义2信息熵 信息熵[19]于1948年由Shannon提出,利用概率与统计方法来表征样本空间所体现的系统无序化程度,进而反映节点在网络中的重要性。信息熵被定义为

(2)

定义3核度中心度 核度中心度指标是结合节点超度和K-shell值,利用欧氏距离公式计算的超网络中节点的核度值,该指标有效改善了超网络K-shell分解方法的区分度。节点vi的核度中心度定义为

(3)

其中,dH(i)为节点vi的超度,Ks(i)为节点vi的Ks值。

定义4超网络最大连通子图的相对大小为网络受到攻击后的最大连通子图的节点数与原始网络总节点数之比,即:

(4)

其中,S为遭受攻击后网络的最大连通子图的大小,N为原始网络的节点数。该方法着重考察移除部分节点后网络结构和功能的变化,通过网络的鲁棒性和脆弱性对排序算法进行客观评价。

定义5超网络自然连通度[20-21]超网络的邻接矩阵A(H)=(aij)N×N为对称矩阵,令λ1≥λ2≥…≥λN为A(H)的特征根,表示网络中所有闭途径数目,则超网络的自然连通度[22]定义为

(5)

其中,λi为超网络邻接矩阵的特征根。该方法基于网络特征谱,通过计算网络中不同长度闭环数目的加权和来刻画网络中替代途径的冗余性,用于反映网络的抗毁性,进而对排序算法进行精确性评价。

2 构造中心性度量指标

超网络由节点及超边组成,通过超边连通的节点之间存在一定的重要度依赖关系。由于邻居节点间的影响是相对重要且直接的,在对节点重要性进行度量时,考虑节点自身属性及邻居节点间的相互影响,提出了局部影响力和全局影响力两种指标。

2.1 局部影响力指标

超网络中节点超度反映节点自身的直接影响力,而节点的重要性不仅与自身属性有关,还依赖于网络中其他节点对其重要度的影响,尤其是邻居节点的贡献。为此,本文基于节点超度引入影响度的概念,来表征邻居节点间的相互影响。

定义6节点vi对节点vj的影响度定义为

(6)

其中,dH(vi)为节点vi的超度,Γ(vj)为节点vj邻居节点的集合。

定义7节点vi和节点vj之间的相互影响度Rw(vi,vj)定义为

Rw(vi,vj)=w(vi,vj)+w(vj,vi)

(7)

显然节点vi和节点vj的邻居节点不同,w(vi,vj)和w(vj,vi)不一定相等。

定义8(局部影响力LI)节点vi的局部影响力LI(vi)定义为

(8)

2.2 全局影响力指标

超网络中节点的影响不仅取决于节点的局部影响,还依赖于节点的全局影响。K-shell分解法[14]是一种从网络整体结构评价节点重要性的全局性指标。该方法的基本思想是通过迭代的方式将网络划分为从核心到边缘的不同层次,越靠近核心的节点越具有影响力。图1b～d分别为1-shell、2-shell和3-shell分解图。

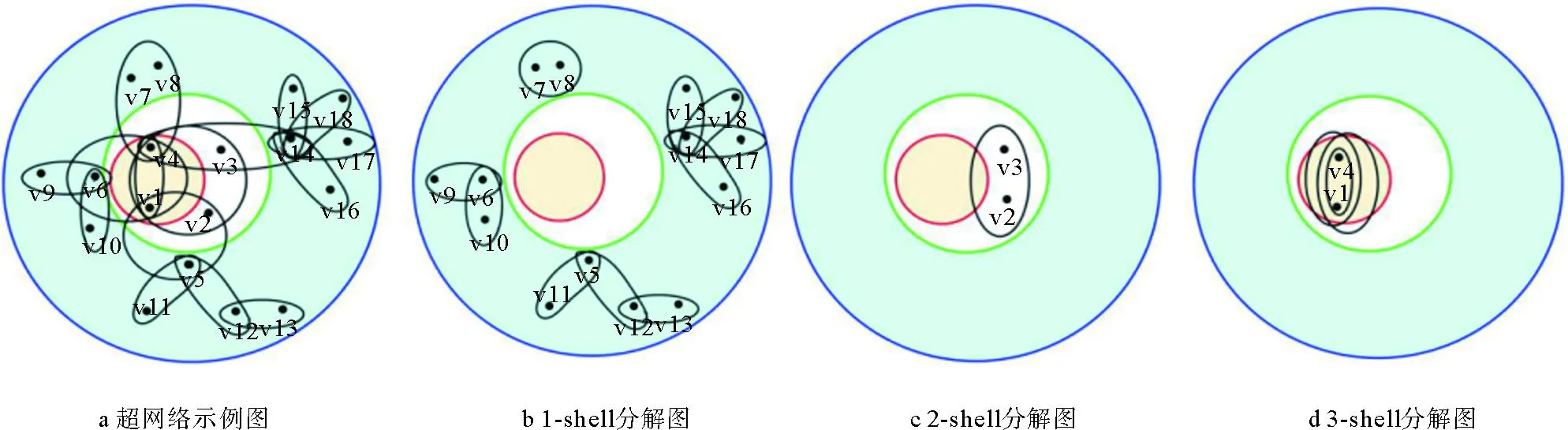
图1 3-shell分解过程示例图[14]

由图1可知,节点1,4均位于超网络的核心位置,具有相同的ks=3,显然这两个节点的影响力是不同的。K-shell分解法无法区分ks值相同的节点的影响,这会导致节点排序结果过于粗粒化,因此,为了更准确地识别影响节点,本文给出衡量节点全局影响力的定义。

定义9(全局影响力GI)考虑到节点邻居数目及所处位置的影响,将节点vi的全局影响力GI(vi)定义为

(9)

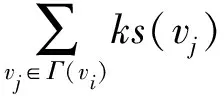
图1所示的网络中,ks=3的节点可以通过全局影响力进行区分:GI(1)=12,GI(4)=14。节点5,6,7,12,15的ks值均为1,其GI值分别为8,9,5,3,2。综上可以看出,GI指标相比ks指标能更进一步区分节点的影响力。

3 多属性决策的重要节点识别算法

节点的局部影响及全局影响对节点重要性识别起着重要作用,但每个属性各有侧重且存在一定差异。本文在考虑网络拓扑结构信息的基础上,选用介数中心性来度量节点在网络连通性方面的重要性,综合考虑节点的局部影响力LI和全局影响力GI,通过熵理论对每个指标赋予不同的权重,提出一种基于熵的多属性决策超网络重要节点识别算法(Entropy Theory-Based Multi-Attribute Centrality of Hypernetworks,简称EBMCH)。算法步骤为

步骤1构造属性矩阵

在评估节点重要性时,对局部影响力、介数中心性以及全局影响力进行归一化处理,根据归一化后的值构造属性矩阵P:

(10)

其中,n为超网络中的节点数,{ai1,ai2,ai3}表示节点的属性。

步骤2计算各属性熵值

在多属性决策问题中,为保证各属性权重分配的合理性,基于熵理论来客观确定各属性权重。如果一个属性的信息熵越小,说明该属性提供的信息量就越大,在综合评价中所起的作用就越大,其权重相应就越高。基于香农熵理论,计算第j项指标的熵值ej:

(11)

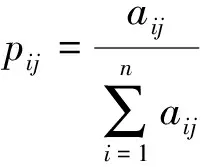
步骤3根据熵值ej计算各指标的权重wj:

(12)

步骤4根据熵权法的结果,计算节点vi的权重因子si:

(13)

步骤5结合节点本身及其邻居节点的权重因子,最终得到节点vi的基于熵的多属性中心性EBMCH(i)为

(14)

4 实证分析

4.1 示例超网络分析

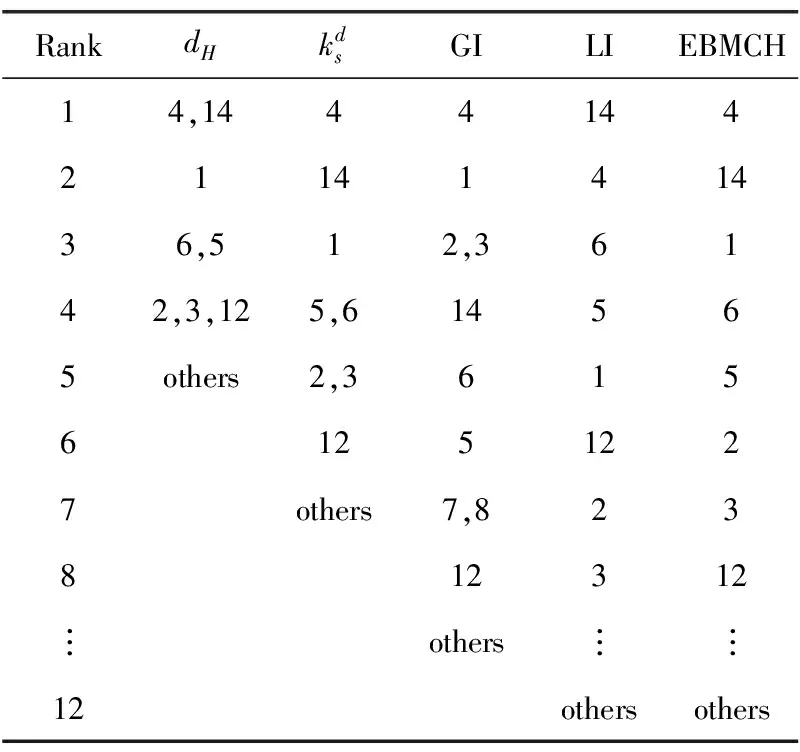
表1 不同指标对示例超网络的排序结果

为了进一步验证本文算法的合理性,从网络拓扑结构和特征谱两个方面来验证本文所提方法的准确性。对比按照不同方法依次移除节点后剩余网络的最大连通子图的相对大小及自然连通度变化情况,结果如图2所示。

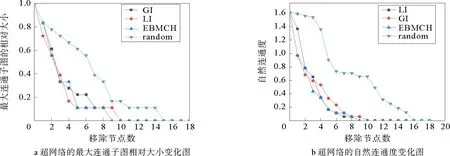
图2 移除节点后的网络最大连通子图相对大小及自然连通度变化图

由图2a可知,EBMCH指标在移除第1,4节点后得到的网络最大连通子图的相对大小值略高于其他指标,而其他节点删除后得到的最大连通子图的相对大小值均小于或等同于其他指标,如图2b,EBMCH指标在移除第2,7节点时的网络自然连通度值略高于其他指标,在删除其他节点时的网络自然连通度值一直处于最低位置。

4.2 实证超网络分析

4.2.1 数据来源

为了进一步验证EBMCH算法的可行性,本文以西宁市公交数据为例,收集了截至2022年2月13日西宁市公交线路及站点的数据,得到577个公交站点以及92条公交线路。基于此数据集构建西宁市公交超网络模型,站点表示超网络中的节点,线路表示超网络中的超边。

4.2.2 实验结果分析

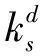
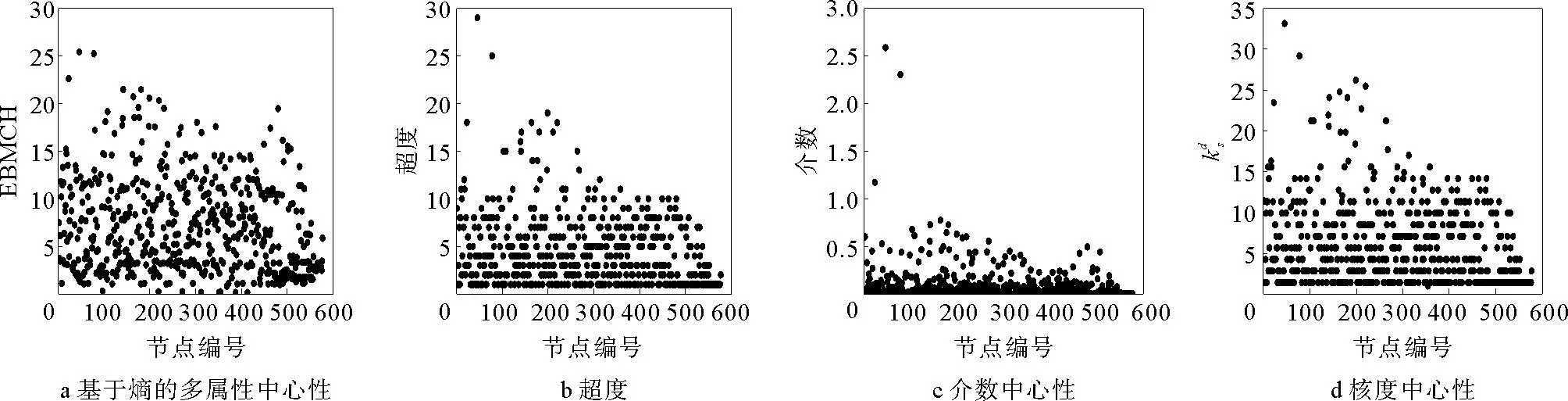
图3 所有节点的基于熵的多属性中心性值、超度值、介数中心性值及核度中心度值

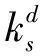
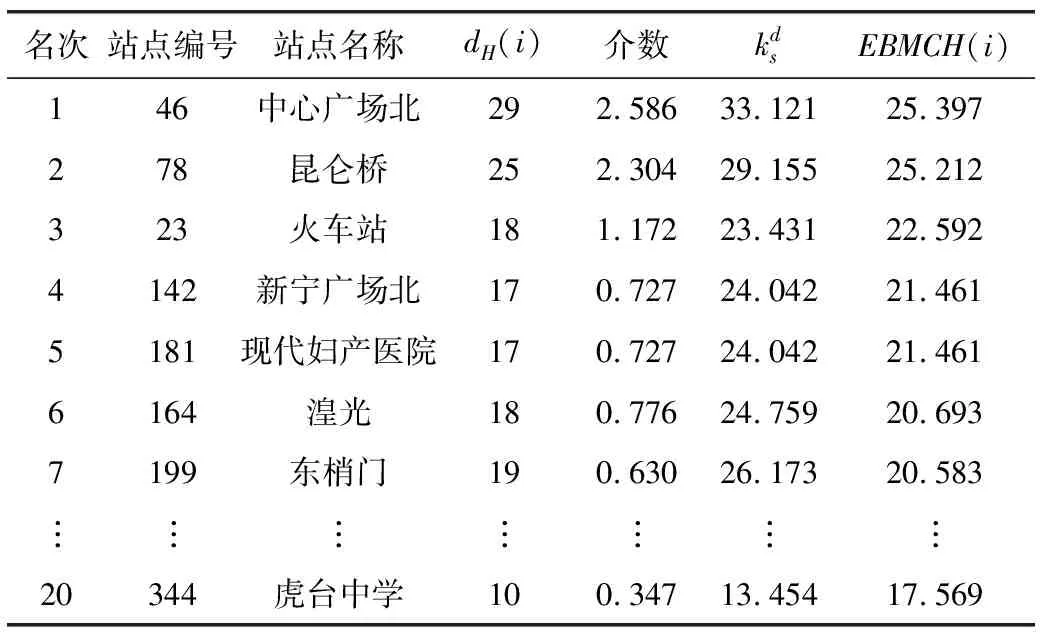
表2 EBMCH排名前20的站点及相应指标

由表2知,节点46和节点78的EBMCH值最大,即识别出的西宁市公交超网络的重要节点分别是中心广场北站和昆仑桥站。这与其他单一指标的识别结果一致。EBMCH值排名第3的是火车站,而其他指标识别排名靠后,相同值较多,火车站作为城市的重要枢纽,其重要性显而易见。由EBMCH识别的4、5名站点位于西宁市城西区域,据智能CT实时数据显示,西宁市四区中最拥堵区域为城西区,由EBMCH指标识别出的站点位于城西区的占45%以上,表明EBMCH指标能更准确、有效地识别公交超网络重要节点。为了进一步验证识别结果的合理性,对比网络最大连通子图相对大小及自然连通度值如图4所示。

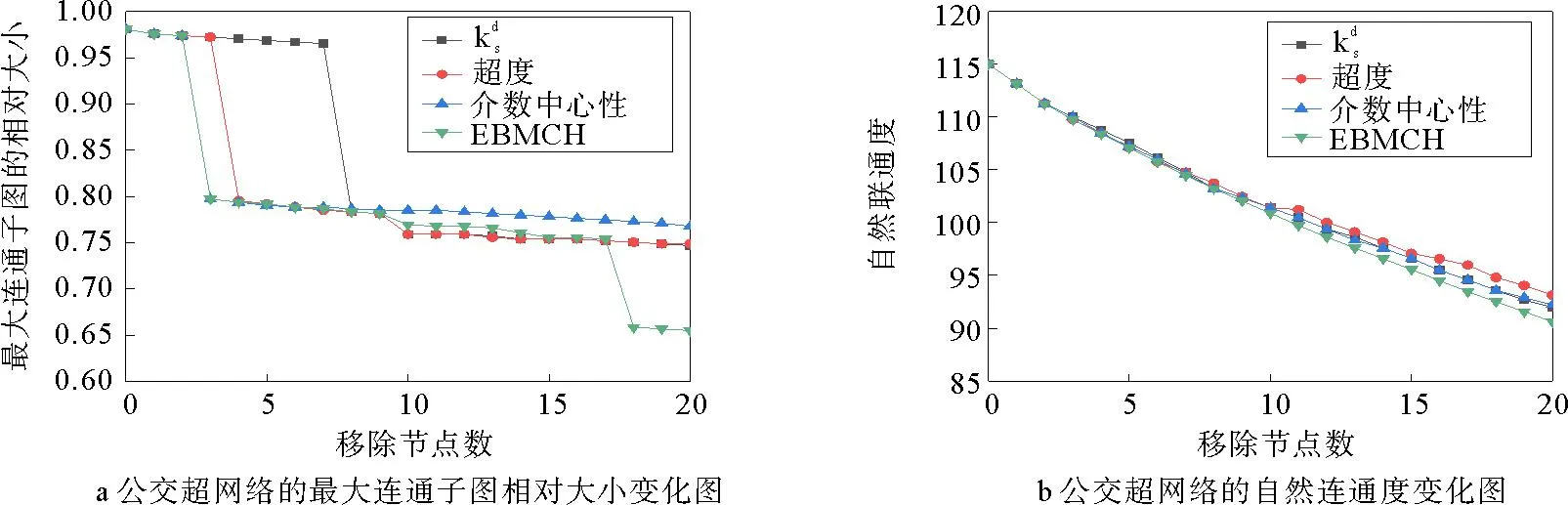
图4 移除节点后的公交网络最大连通子图相对大小及自然连通度变化图

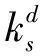
5 结论