极点极线视域下圆锥曲线试题的应用探索

福建省泉州市晋江市紫峰中学(362200)曾晓丽

定义1(极点, 极线) 若圆锥曲线C:Ax2+Bxy+Cy2+Dx+Ey+F=0,已知点P(x0,y0)(非中心),直线,则称点P(x0,y0)是直线l关于圆锥曲线C的极点,直线l称为P点关于曲线C的极线.

性质1若P在圆锥曲线C上,则P关于C的极线即C为在P处的切线.

性质2(配极原理)关于圆锥曲线C,若P在Q的极线上,则Q在P的极线上,并称P,Q关于C调和共轭.

性质3(极线即切点弦)过圆锥曲线C外的一点P作PA,PB切C于A,B两点,则AB为P关于C的极线.

定义2(调和点列)若直线l上四个点A,B,C,D满足,则A,B,C,D是一组调和点列.

定义3(调和线束)四条直线l1,l2,l3,l4相交于一点,记直线li,lj的夹角为αij,若,则l1,l2,l3,l4是一簇调和线束.

性质4(调和点列与调和线束的转换) 若直线上有四个点A,B,C,D, 直线外有一点P, 若A,C;B,D调和, 则PA,PC;PB,PD调和;反之也成立.

性质5(极点极线与调和点列的转换)圆锥曲线C上有A,B两点,若P,Q;A,B是调和点列,则P,Q关于C调和共轭.

即证P,Q关于C调和共轭.

引理若A1,A2;B1,B2在圆锥曲线C上,A1B1∩A2B2=P,A1B2∩A2B1=Q,则P,Q调和共轭.

证明在A1B1上取Q1P使得A1,B1;P,Q1调和,由性质5 有Q1在P的极线上.设QQ1∩A2B2=Q2, 由QA1,QB1;QP,QQ1调和, 有B2,A2;P,Q2调和, 故Q2在P的极线上.于是Q1Q2为P的极线,而Q∈Q1Q2,故Q在P的极线上,即P,Q关于曲线C调和共轭.

性质6(平行线被调和线束平分)l1,l3;l2,l4是调和线束,若l//l1交l2,l3,l4于A,B,C,则B为A,C中点.

证明设线束交于P点,则

故AB=BC.即证B为A,C中点.

例1(2023 年高考乙卷理科第20 题) 已知椭圆的离心率为,点A(-2,0)在C上.

(1)求C的方程;

(2)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明: 线段MN的中点为定点.

解(1)由题意b= 2,得知:,从而a=3,所以曲线C的方程为:.

(2) 证明: 令B(-2,3), 如图1, 在线段PQ上取一点E使得, 即B,E;P,Q为调和点列,又P,Q是椭圆C上的点, 根据性质5可知:B,E关于椭圆C调和共轭,所以点E在点B的极线上,点B的极线l为:.又因为A(-2,0),所以点A也在极线l上,即直线AE就是极线l.因为B,E;P,Q为调和点列,所以AB,AE;AP,AQ为调和线束.由题可知: 直线AB:x= -2, 所以AB//y轴, 又因为直线AP,AE,AQ分别与y轴交于点M,D,N,由性质6 可知:D为MN的中点.由于直线AE为定直线,所以它与y轴的交点为定点,即D(0,3).

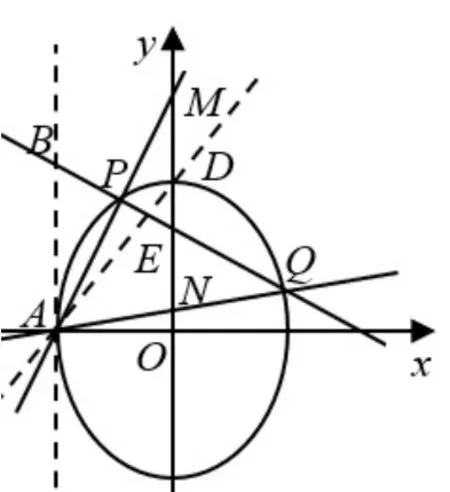
图1

例2(2023 年高考新课标II 卷第21 题)双曲线C中心为原点,左焦点为,离心率为.

(1)求C的方程;

(2)记C的左,右顶点分别为A1,A2,过点(-4,0)的直线C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于P,证明P在定直线上.

解(1)由题意,则a=2,b2=16,双曲线为.

(2)证明令Q(-4,0),如图2, 在MN上取P1̸=Q使得M,N;Q,P1调和,由性质5 有P1在Q的极线上,由题知点Q的极线l为:x= -1, 并且得到调和线束PM,PN;PQ,PP1, 设PP1∩A1A2=P2,则直线A1A2与PM,PN,PQ,PP1分别交于点A1,A2,Q,P2, 即A1,A2;Q,P2为调和点列, 又A1,A2在双曲线C上,所以Q,P2关于双曲线C调和共轭,即P2在Q的极线上, 所以, 直线P1P2就是极线l, 又因为P∈P1P2,所以点P在极线l上,即x=-1 上.

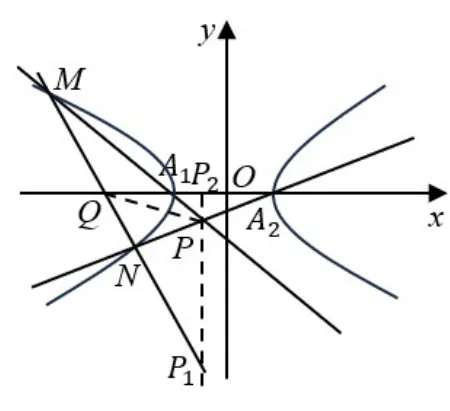
图2

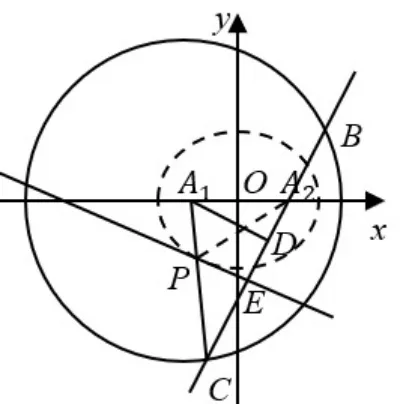
图3-1

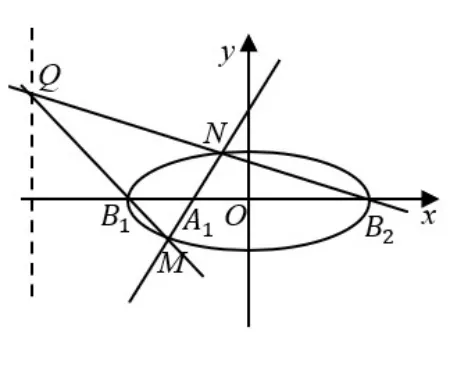
图3-2

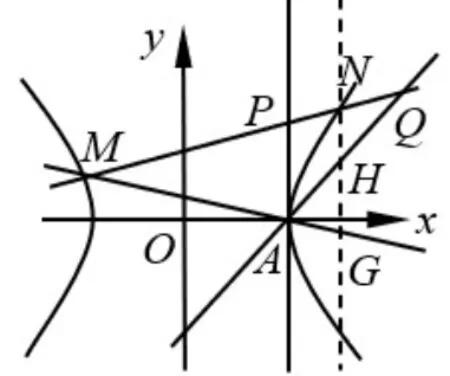
图4

例3(福建省2023 届适应性试卷第21 题) 已知圆A1:(x+1)2+y2=16,直线l1过点A2(1,0)且与圆A1交于点B,C,BC中点为D,过A2C中点E且平行于A1D的直线交A1C于点P,记P的轨迹为Γ.

(1)求Γ 的方程;

(2)坐标原点O关于A1,A2的对称点分别为B1,B2,点A1,A2关于直线y=x的对称点分别为C1,C2,过A1的直线l2与Γ 交于点M,N,直线B1M,B2N相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.

①∆QB1C1的面积是定值; ②∆QB1B2的面积是定值; ③∆QC1C2的面积是定值.

解(1) 由题意得,A1(-1,0),A2(1,0).因为D为BC中点, 所以A1D⊥BC, 即A1D⊥A2C, 又PE//A1D, 所以PE⊥A2C,又E为A2C的中点,所以|PA2| = |PC|,所以|PA1|+|PA2|=|PA1|+|PC|=|A1C|=4>|A1A2|,所以点P的轨迹Γ 是以A1,A2为焦点的椭圆(左、右顶点除外).设,其中a>b>0,a2-b2=c2.则2a= 4,a= 2,c= 1,.故.

(2)结论③正确,下证∆QC1C2面积为定值.

证明因为B1,B2,M,N都在椭圆Γ 上, 由题易知B1B2∩MN=A1,B1M∩B2N=Q,则A1,Q关于椭圆Γ调和共轭,即Q在点A1的极线上,又因为极点A1的极线为x= -4,所以点Q在直线x= -4 上.所以点Q到C1C2的距离d=4,则

例4(2023 年5 月福州市高三毕业班质量检测)已知双曲线的右顶点为A,O为原点,点P(1,1)在C的渐近线上,∆PAO的面积为.

(1)求C的方程;

(2)过点P作直线l交C于M,N两点,过点N作x轴的垂线交直线AM于点G,H为NG的中点, 证明: 直线AH的斜率为定值.

解(1) 因为P(1,1) 在C的渐近线上, 所以a=b,因为A(a,0),所以∆PAO的面积为,解得a=1,所以b=1,所以C的方程为x2-y2=1.

(2) 在线段MN上取点Q使得,即M,N;P,Q为调和点列, 又M,N是曲线C上的点, 根据性质5 可知:P,Q关于曲线C调和共轭, 设Q(xQ,yQ),P(xP,yP)则有xPxQ-yPyQ= 1,又P(1,1)代入有xQ-yQ= 1.因为点P(1,1)的极线l1:x-y= 1,所以点Q在极线l1上,又因为点A(1,0),所以点A也在极线l1上,即直线AQ就是极线l1.因为M,N;P,Q为调和点列,则AM,AN;AP,AQ为调和线束.又因为NH⊥x轴,由题易知直线AP为:x= 1, 所以NH//AP, 并且直线NH与直线AN,AQ,AM分别交于点N,H,G,则由性质6 可知:H即为线段NG的中点.即中点H在直线AQ上,所以直线AH即为极线l1:y=x-1,所以直线AH的斜率为1.

例5(2022 年高考全国乙卷理科第20 题) 已知椭圆E的中心为坐标原点, 对称轴为x轴、y轴, 且过A(0,-2),两点.

(1)求E的方程;

(2)设过点P(1,-2)的直线交E于M,N两点, 过M且平行于x轴的直线与线段AB交于点T, 点H满足.证明: 直线HN过定点.

解(1) 设椭圆E的方程为mx2+ny2= 1, 过A(0,-2),,则,解得,所以椭圆E的方程为:.

(2)定点为(0,-2),证明如下:

证明在线段MN上取点Q使得,即M,N;P,Q为调和点列, 又M,N是椭圆E上的点, 根据性质5 可知:P,Q关于椭圆E调和共轭.设Q(xQ,yQ),P(xP,yP) 则有, 又P(1,-2)代入有,而直线,所以Q∈AB, 即Q为AB与MN的交点.如图5, 可知M,N;P,Q为调和点列,则AM,AN;AP,AQ为调和线束.

图5

又根据题意过M作MT//x轴,且直线AP:y= -2,所以MT//AP, 直线MT分别与直线AM,AQ,AN交于点M,T,H1, 根据性质6 可知T为MH1的中点.又因为,所以T为MH的中点,即H与H1重合,所以A,H,N三点共线,即直线HN必过定点A(0,-2).

极点极线的问题若只是以高中的角度来看并不是太复杂,在高中解析几何中即可用来求切线、切点弦方程,易学易懂.还可用来确定割线交点的位置,在处理一些动直线过定点和动点在定直线上时很容易找到答案,极点极线的应用在高考中出现频率较高,此处只是将极点极线的性质直接拿来使用,更多的性质以及性质的证明在大学高等几何中会学到,此处无需深究.