从期望与方差的角度谈高考英语的“七选五”题

广东省佛山市乐从中学(528315)林国红

一、研究的源由

高考英语中有一类叫“七选五”的试题,该题一般出现在试卷阅读部分的第二节,是一篇缺少5 个句子的文章,提供7个选项(A,B,C,D,E,F,G),要求学生根据文章的结构、内容,从文后的7 个选项中选出5 个最佳选项填入文中相应空白处,使文章完整、连贯通顺.即“七选五”试题共有5 道选择题,给出7 个选项,其中有2 个多余选项(干扰选项),考生从中选择5 项依次填入每道题中,每题只有一个正确选项,每选对一题得2.5 分.

若一位同学的英语水平不好,在做“七选五”题时,若通过蒙题的方式答题,能做对多少题? 平均得分又是多少?

注所谓的“蒙”题,是指这篇文章你完全看不懂(或者不看文章内容),5 个空白处随便填入一个选项.

二、第一种蒙题方式的探究

“七选五”试题中,每题只有一个正确选项,若不考虑同一选项被多次选择的情况(即选项不能重复),对5 道题全部随机作答,记答对的题数为X0,求X0的分布列与数学期望.

文[1]对此问题进行深入的探究,得到X0的分布列.

0 1 2 3 4 5 P 1214 2520 905 2520 320 2520 70 2520 10 2520 1 2520

并求得X0的数学期望:

另外,可求得X0的方差:

三、第二种蒙题方式的探究

“七选五”试题中,每题只有一个正确选项,若同一选项可被多次选择,即每个空的选项可以部分相同,也可以全部相同,此时对5 道题全部随机作答,记答对的题数为X,求X的分布列,数学期望与方差.

下面的讨论约定“七选五”试题的正确答案为ABCDE,记Ω = {A,B,C,D,E,F,G},Ω1= {A,B,C,D,E},Ω2={G,F}.

3.1 选项全部相同(即MMMMM 型,M ∈Ω)

记答对的题数为X1, 则X1∈{0,1}.显然, 随机变量X1服从两点分布,其分布列为:

X1 0 1__P 2/7 5/7

所以X1的数学期望为.方差为.

3.2 选项部分相同

1.MMMMN型,M,N∈Ω

记答对的题数为X2, 则X2∈ {0,1,2}.因为是MMMMN型, 所以只需从7 个选项中选出2 项, 并按一定的顺序填入5 个空中,共有种填法.

(1)当X2=0 时,有4 种情形:

①若M,N∈Ω2(如FFFFG型),有2 种选法,此时5个空中选4 个空填F,1 个空填G,则有种填法;

②若M∈Ω2,N∈Ω1(如FFFFA型),有2×5 种选法,此时只需第一个空填F,在剩余的4 个空选3 个填F,1个空填A,则有种填法;

③若M∈Ω1,N∈Ω2(如AAAAF型),有2×5 种选法, 此时只需第一个空填F, 在剩余的4 个空全填A, 则有种填法;

④若M,N∈Ω1(如AAAAB型), 有5 × 4 种选法,此时只需第一个空填B, 在剩余的4 个空全填A, 则有种填法.所以, 当X2= 0 时, 共有10+40+10+20=80 种填法.

(2)当X2=1 时,有3 种情形:

①若M∈Ω2,N∈Ω1(如FFFFA型),有2×5 种选法, 此时只需第一个空填A, 在剩余的4 个空全填F, 则有种填法;

②若M∈Ω1,N∈Ω2(如AAAAF型),有2×5 种选法,此时只需第一个空填A,在剩余的4 个空选3 个填A,1个空填F,则有种填法;

③若M,N∈Ω1(如AAAAB型),有5×4 种选法,此时第一个与第二个空只能填A,在剩余的3 个空选2 个填A,1 个空填B,则有种填法.所以,当X2= 1时,共有40+10+60=110 种填法.

(3) 当X2= 2 时, 只有1 种情形:M,N∈ Ω1(如AAAAB型), 有5 × 4 种选法, 此时第一个需填A, 第二个空需填B,在剩余的3 个空全填A,则有种填法.从而可得X2的分布列为:

X2 0 1 2__P 80_________________210 110 210___20 210_

评注后述各种类型的解答与本类型的思路一致,限于篇幅,只给出最后的结果,不再分析详细的求解过程.

2.MMMNN型,M,N∈Ω

记答对的题数为X3, 则X3∈{0,1,2}, 可得其分布列为:

X3 0 1 2__P 180_______420 180 420___60 420_

3.MMMNO型,M,N,O∈Ω

记答对的题数为X4,则X4∈{0,1,2,3},可得其分布列为:

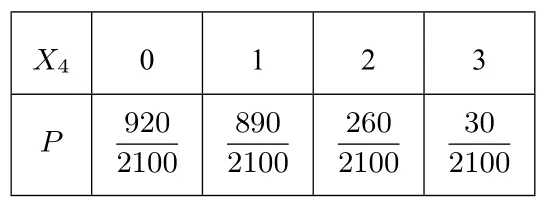
X4 0 1 2 3 P 920 2100 890 2100 260 2100 30 2100

4.MMNNO型,M,N,O∈Ω

记答对的题数为X5,则X5∈{0,1,2,3},可得其分布列为:

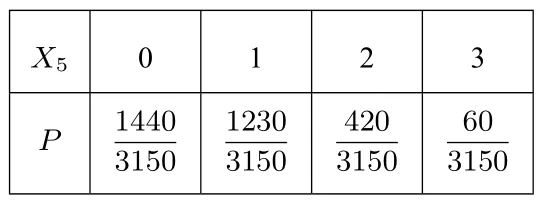
X5 0 1 2 3 P 1440 3150 1230 3150 420 3150 60 3150

5.MMNOP型,M,N,O,P∈Ω

记答对的题数为X6,则X6∈{0,1,2,3,4},可得其分布列为:

X6 0 1 2 3 4 P 3940 8400 3160 8400 1080 8400 200 8400 20 8400

四、蒙题的期望与方差分析

4.1 期望分析

显然E(X1) =E(X2) =E(X3) =E(X4) =E(X5) =E(X6) =E(X0),也就是说不管用哪一种方式蒙题,期望做对的个数都是一样的! 这样的结果是巧合吗?

事实上, 这个结果并不是巧合, 原因如下: 记事件Ai(i= 1,2,3,4,5)表示第i个空答对,则.由全概率公式,得:

记答对的题数为X, 则X服从二项分布, 即, 于是, 所以采用蒙题方式答题, 期望做对的个数为,和有没有重复选项没有关系.

4.2 方差分析

五、蒙题方式答题的一些结论

通过两种蒙题方式的分析,可以知道:

(2)高考英语“七选五”题型的设置是科学的,也是公平的,保证用蒙题方式答题的期望是相同的,能有效防止通过蒙题的方式得到高分;

(3)英语的“七选五”题采用蒙题的方式答题,其期望得分是非常低的,所以蒙题是非常不明智的举措,如果你不想落入这种窘况,那就只有好好学习了!

(4)如果英语水平不好,考试时确实看不懂文章的意思,只能用蒙题方式答题.从方差的角度看: 如果想保底获得一点分数,可以填写5 个选项全部相同,这样最保险;如果想博取更高的分数,则可以填写5 个选项均不相同,在运气好的情况下,有可能得满分,但是“高回报意味着高风险”,因为在选项不能重复情形下,全蒙错的概率为,即有接近一半的概率得0 分,这是各类蒙题方式中,全错概率最高的.

六、进一步思考

在英语“七选五”题中,若考生能正确答对某题(或某几题),剩余的题目完全不懂,采用蒙题方式进行答题,那么答对题数的期望与方差又如何计算?

这类情况可以仿照前述的方法进行分析,留给感兴趣的读者自行研究.