砂性基础大直径单桩水平承载力预测模型
陈大江,詹懿德,张 强,张 毅,郑 莉
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;2.浙江华东工程咨询有限公司,浙江 杭州 311122;3.浙江大学 海洋学院,浙江 舟山 316021)
0 引 言
单桩基础在世界海上风电项目中应用最为广泛[1-2]。目前所采用的海上风电大直径单桩基础的长径比(埋深与桩径之比)一般小于10[3]。在复杂的海洋环境下,单桩基础设计主要受水平承载特性的控制[4]。截至2020年底,江苏省海上风电装机并网规模为573万kW,占全国的63.7%。江苏岸外辐射沙洲是江苏省重要的海上风电规划区域[4],因此研究江苏岸外辐射沙洲海域大直径单桩水平承载特性具有重要的工程意义。当前,众多学者采用数值模拟方法研究桩参数[5-6]、土体参数[3,7]和环境因素[8]等对单桩水平承载特性的影响规律,发现桩径和埋深对单桩水平承载力的影响非常显著。熊根[9]基于有限元软件Abaqus开展大直径单桩水平承载特性研究,指出当桩径为5 m时,埋深大于40 m后,单桩水平载荷-位移曲线不再发生变化。杨永垚[10]基于所提出的单桩水平承载力解析解,开展桩基承载力敏感性分析,发现单桩水平承载力随桩径或埋深的增大而增大。周茂强等[11]采用Abaqus软件开展大直径钢管单桩水平承载特性敏感性分析,数值模拟结果表明随桩径增大,桩身水平位移逐渐减小,单桩水平极限承载力线性增大。目前,许多学者广泛开展桩径和埋深对单桩水平承载特性的影响研究,但缺乏考虑桩径和长径比影响的单桩水平极限承载力预测模型。
本文开展江苏竹根沙海域现场试桩试验,采用有限元软件Abaqus建立等效大直径单桩水平受荷分析数值模型,开展单桩水平承载特性数值模拟,研究桩径和长径比对单桩水平极限承载力的影响规律,提出大直径单桩水平极限承载力预测模型,研究成果可为江苏竹根沙海域海上风电大直径单桩的承载力预测提供模型支持。
1 江苏竹根沙海域现场试桩
某海上风电项目位于江苏岸外辐射沙洲海域,开展该海域的现场试桩试验,获取单桩桩身挠度和弯矩曲线。
1.1 试桩背景介绍
试桩场地海域如图1所示,在桩入土深度范围内的岩土体性质为第四系沉积物,土体分层繁杂,表层以砂土为主。
图1 试桩场区位置[11]
1.2 现场试桩试验
开展单桩水平静力载荷试验,试验装置如图2所示,试桩桩径为1.8 m,桩长为51.0 m,壁厚为25.0 mm,埋深为29.0 m,悬臂段长22.0 m,长径比(埋深与桩径之比)为16.1,水平力加载点位于桩顶下0.5 m处。
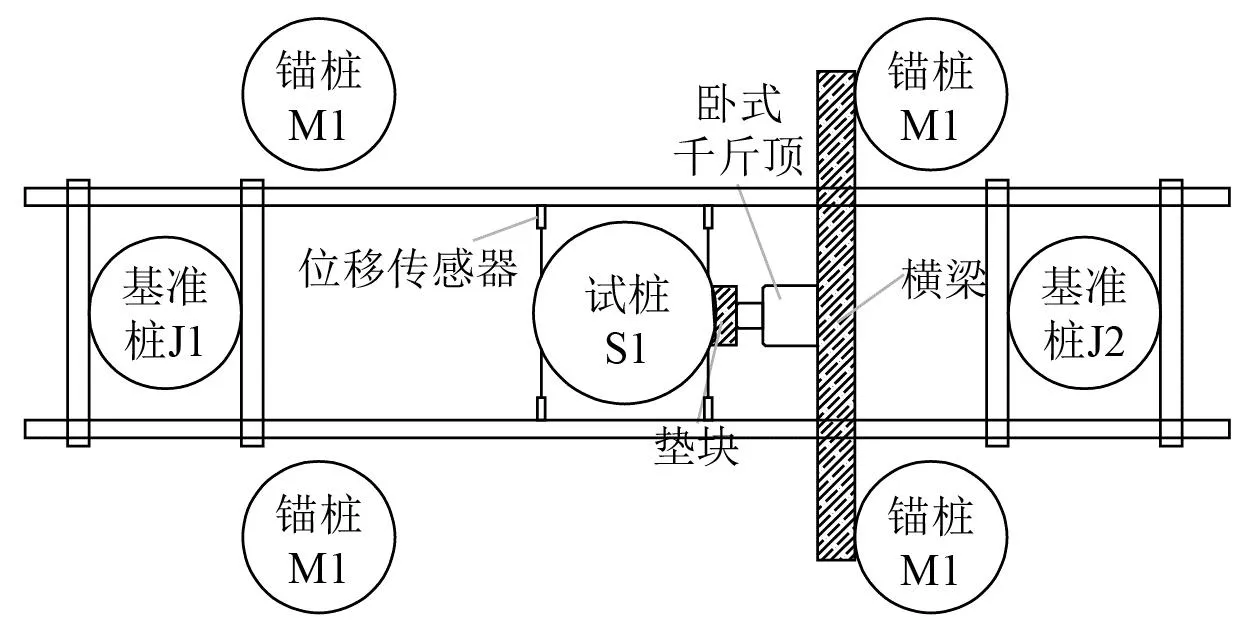
图2 现场水平静力载荷试验
桩身挠度采用北京智利科学仪器厂CX-08A测斜仪进行测量,桩身应变采用日本Neubrex公司的光纳仪(型号NBX-6045L)自动完成。所得部分单桩桩身挠度和弯矩曲线如图3所示。
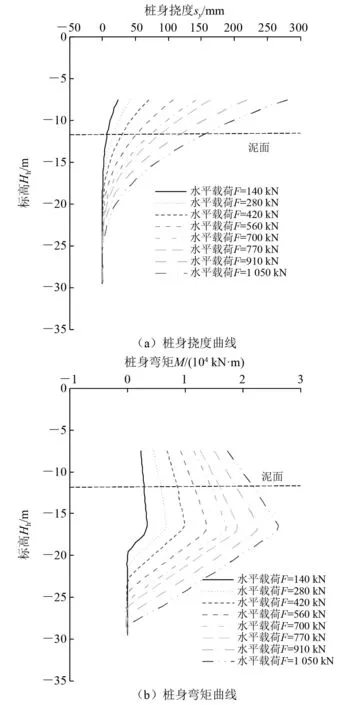
图3 现场试桩数据
由图3可知:试桩近桩底处几乎未被扰动,呈现典型的柔性桩特征;随着水平载荷的增大,试桩桩身最大弯矩逐渐增大,所在位置逐渐下移,在泥面以下4.0~4.5 m,即2.2D~2.5D(D为桩径)。
2 大直径单桩水平受荷等效数值模型
考虑到该海域地质条件较为复杂,土体分层繁多且以砂土为主,因此采用单层砂土进行数值分析。开展单桩水平受荷数值模拟分析,使在单层砂土中所得试桩的水平载荷-位移曲线与实际试桩试验结果相符,校准单层砂土模型参数,为后续研究提供合理的桩基模型。
图4为采用有限元软件Abaqus所构建的试桩数值模型,考虑到几何形状和载荷的对称性,选取1/2进行分析。整个土体模型考虑为半圆柱体,截面半圆的直径为20D,土体底部距离桩底的垂向距离为10D。模型整体采用C3D8R类型的网格,并控制网格属性为结构化网格。对于模型整体边界条件的设置,考虑对称性,在模型对称面限制垂直于该面的位移,在模型底部采用固定支座约束所有方向的位移,在模型外围边界则对径向位移进行约束。
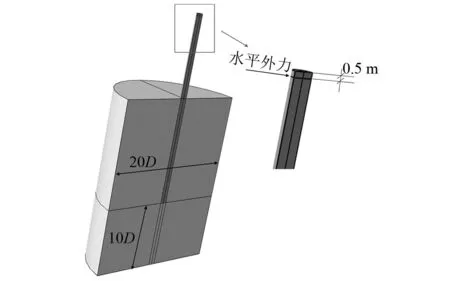
图4 现场试桩Abaqus数值模型
桩的长度、壁厚、入土深度和水平受荷点高度均参照现场试桩试验进行设置,该试桩考虑为实心桩,桩的弹性模量参照式(1)进行转换,桩的密度参照式(2)进行转换。模型参数如表1所示。
(1)
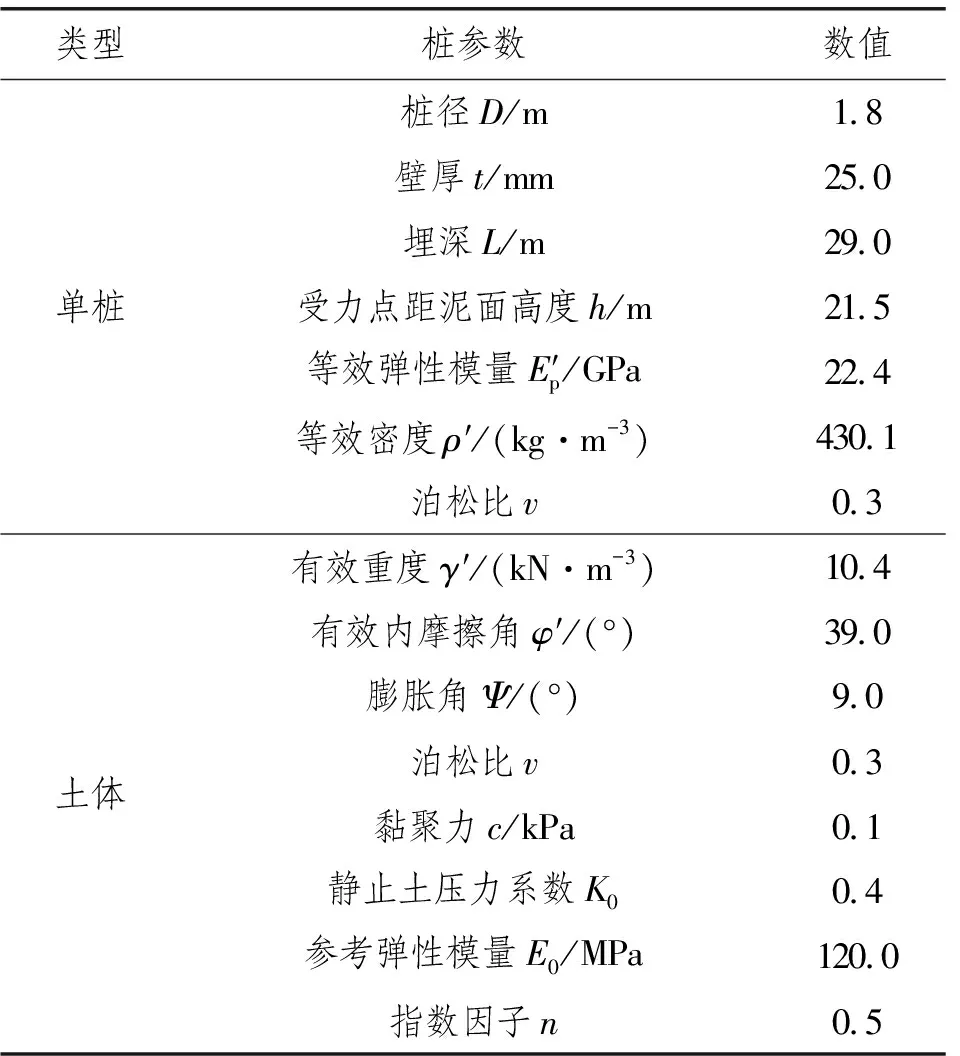
表1 试桩模型参数
(2)
式(1)和式(2)中:Ep和Ip分别为管桩的弹性模量和截面惯性矩;E′p和I′p分别为简化后实心桩的弹性模量和截面惯性矩;ρ为管桩的密度,一般取7 850 kg/m3;ρ′为转换后实心桩的密度;t为壁厚。土体弹性模量采用线弹性模型,计算式为
(3)
式中:Es为砂土的弹性模量;E0为土的参考弹性模量;σ3为最小主应力;pa为大气压,pa=101 kPa;n为指数因子。
此外,桩-土之间的相互作用采用法向硬接触、切向罚函数进行设置。罚摩擦因数设置为tan(0.5φ′)。桩-土之间的相对位移容差设置为2 mm[3]。
基于表1中的数值模型数据,对所建立的现场试桩模型开展单桩水平受荷数值模拟,所得桩受力点处水平载荷-位移曲线如图5所示。由图5可知,数值模拟结果与现场试桩所得结果相符很好,说明所采用的大直径单桩水平受荷等效数值模型合理可靠。
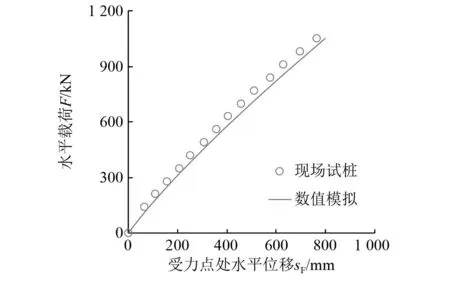
图5 现场试桩与数值模拟所得桩受力点处水平载荷-位移曲线
3 大直径单桩水平极限承载力预测模型
3.1 数值模拟结果
在所建大直径单桩水平受荷等效数值模型(见图4)基础上,构建桩径为2、3、4、5 m,长径比L/D为4、6、8、10、12的桩-土模型,泥面以上桩长设置为1D,模型参数如表1和表2所示,所得各桩-土模型的水平极限承载力如表3所示。

表2 桩模型参数
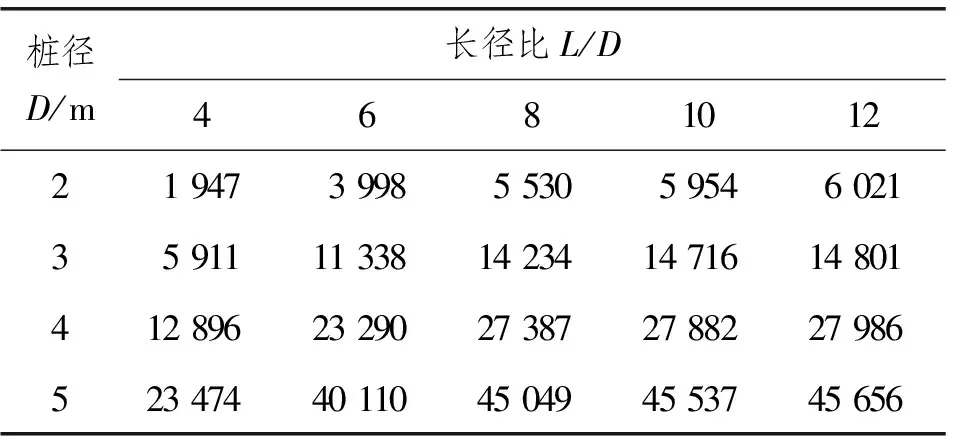
表3 各桩-土模型水平极限承载力
3.2 预测模型建立
为将数值模拟所得单桩水平极限承载力无量纲化,选取桩径为3 m、长径比为8的桩-土模型作为基准模型,在此基础上,提出单桩水平极限承载力因子β计算式为
(4)
式中:Fc为某桩-土模型的水平极限承载力;F0为基准模型的水平极限承载力。
基于式(4),获得各桩-土模型的水平极限承载力因子如表4所示。
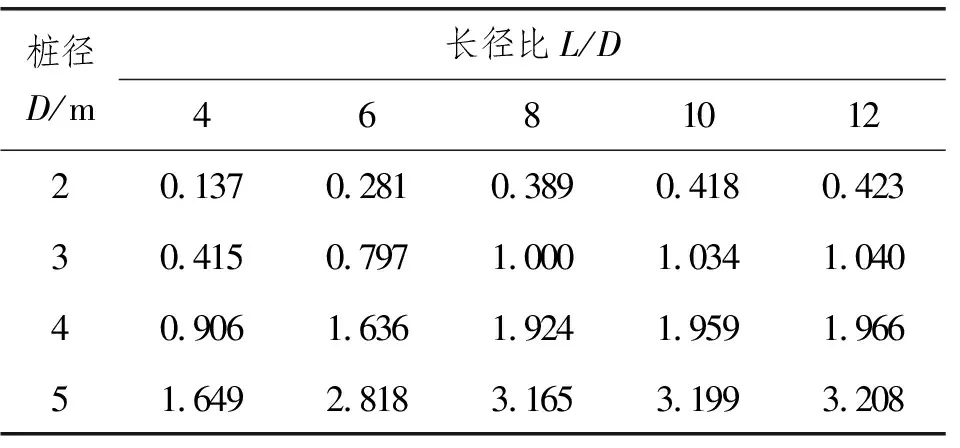
表4 不同桩-土模型水平极限承载力因子β
基于表4,采用幂函数建立单桩水平极限承载力因子β与桩径D的相关关系:
β=MDN
(5)
式中:M和N为待拟合参数。
不同长径比对应的拟合参数M和N的取值如表5所示。
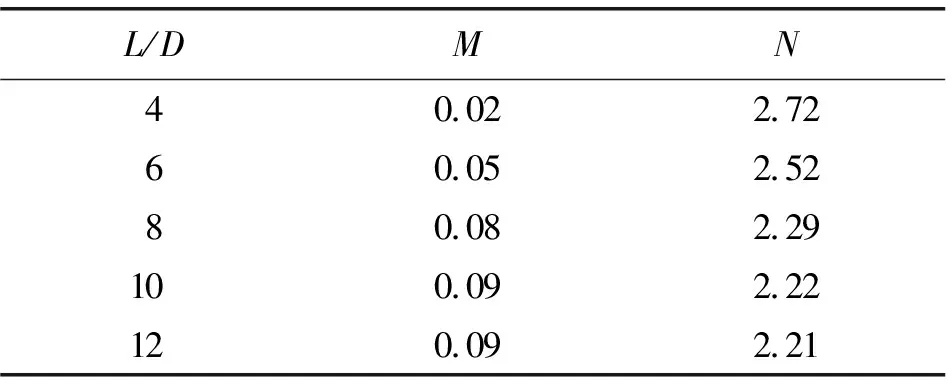
表5 不同长径比时拟合参数M和N取值
进一步地,拟合参数M和N与长径比L/D之间的相关关系如图6所示。采用二次函数进行拟合,如式(6)和式(7)所示,可以看到,拟合效果均非常优异。
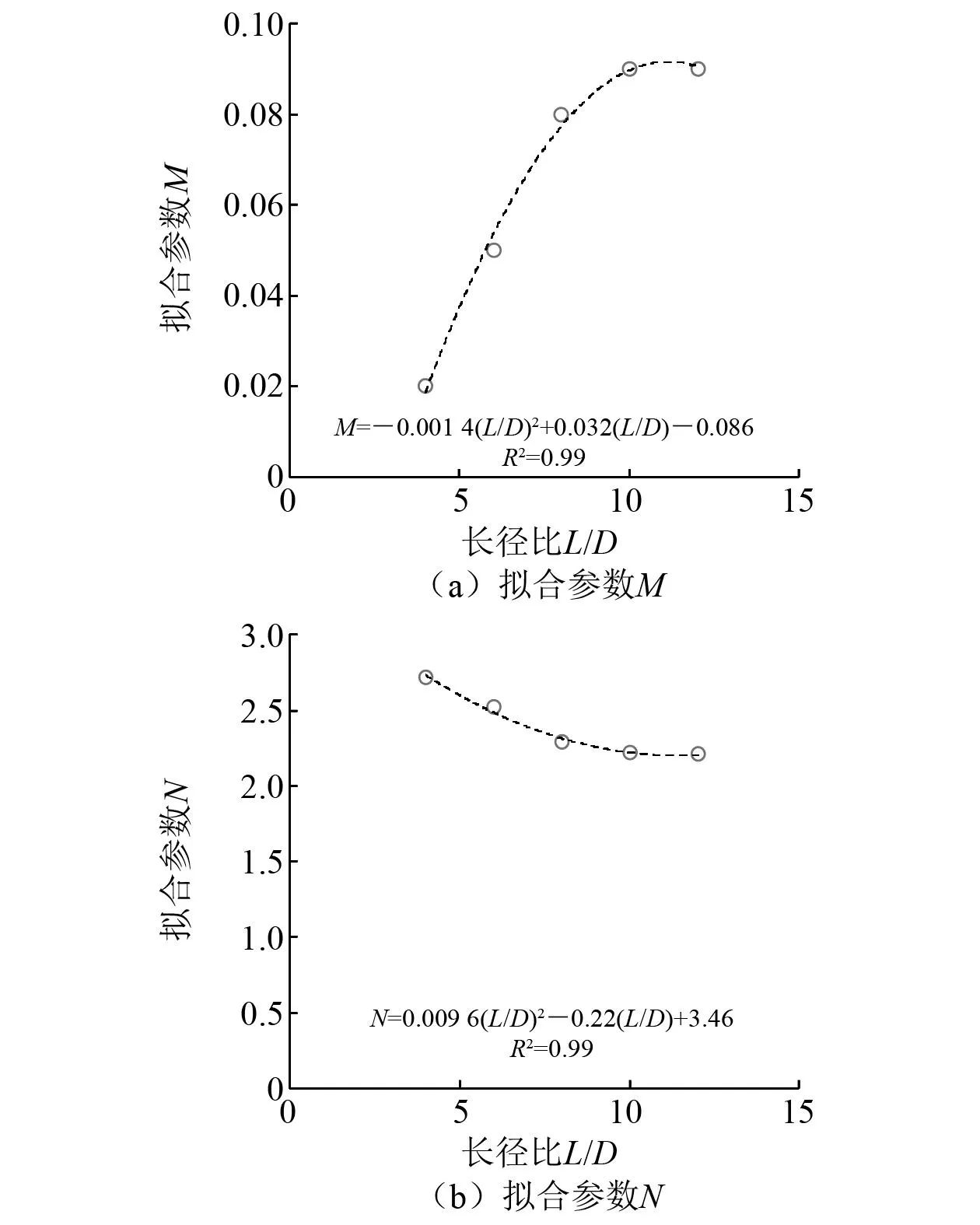
图6 拟合参数M和N与长径比L/D的相关关系
M=-0.001 4(L/D)2+0.032(L/D)-0.086
(6)
N=0.009 6(L/D)2-0.22(L/D)+3.46
(7)
将拟合式(6)和式(7)代入式(4)和式(5),即可得到大直径单桩水平极限承载力F′预测模型:
F′=[-0.001 4(L/D)2+0.032(L/D)-0.086]·
D0.009 6(L/D)2-0.22(L/D)+3.46F0
(8)
3.3 预测模型验证
基于大直径单桩水平极限承载力预测模型,对表3中各桩-土模型的水平极限承载力进行预测,将表3中各桩-土模型所对应的桩径D、长径比L/D代入式(8),得出各桩-土模型水平极限承载力预测值F′。采用平均相对误差(Absolute Average Relative Error Percentage,AAREP)对预测值的准确性进行分析,计算公式为
(9)
(10)
式(9)和式(10)中:N为试验工况总数;S′为预测值;S为试验值;Dp为试验值与对应预测值之间的相对误差。
所得水平极限承载力预测值与试验值的关系如图7所示。由图7可知,单桩水平极限承载力预测值与数值模拟试验结果相符很好,平均相对误差仅4.9%,最大相对误差为10.9%。
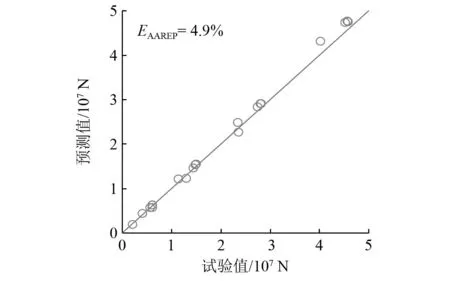
图7 单桩水平极限承载力预测结果
4 结 论
开展江苏某海域现场试桩试验,基于有限元软件Abaqus建立水平受荷单桩分析数值模型,开展单桩水平承载特性数值模拟研究,提出大直径单桩水平极限承载力预测模型,主要结论如下:
(1)试桩的桩身挠度在近桩底处趋于零,呈现典型的柔性桩特征;随着水平载荷的增大,试桩桩身最大弯矩逐渐增大,所在位置逐渐下移,在泥面以下4.0~4.5 m,即2.2D~2.5D。
(2)提出大直径单桩水平极限承载力预测模型,采用该模型对单桩水平极限承载力进行预测,所得预测结果的平均相对误差仅4.9%,最大相对误差为10.9%。该模型可基于试桩试验的单桩水平极限承载力数据对该海域所有不同桩径和长径比的单桩水平极限承载力进行预测。

