一种启发式自优化的紫外线消毒机器人路径规划方法

余一聪，骆绍烨，许城涛，张勇敢，蔡荣贵，2

（1.莆田学院 新工科产业学院， 福建 莆田 351100，2.厦门金龙联合汽车工业有限公司，福建 厦门 361006）

1 研究背景

新冠病毒的全球蔓延，对我国产业产生许多负面影响，疫情让大家对公共环境卫生问题尤为关注。目前有许多杀毒技术被提出，如紫外线杀毒已被证实有效，不污染环境。紫外线杀毒需满足一定要求，即特定的紫外线波长、照射剂量和时间等[1]。大部分紫外线杀毒装置采用定点方式安置，机动性不足、耗费人力等。通过在移动式机器人上装载紫外线消毒装置，能够让机器人在特定的区域范围内自主移动进行杀毒，充当疫情“志愿者”，降低人力成本，提高公共卫生应急响应能力。

在实际复杂环境特定区域下，往往消毒区域复杂且存在诸多障碍物，移动式紫外线消毒机器人常因移动轨迹未优化，使得消毒区域的全覆盖目标难以实现。因此，如何实现在给定区域利用路径规划算法给出最佳的移动轨迹，同时根据移动中出现的障碍物情况实时调整移动轨迹，获得最佳的消毒移动轨迹，已成为紫外线消毒机器人当前的研究热点。本研究中，首先把特定的消毒区域切割成许多小网格，并考虑每一个网格需达到全覆盖，当满足这个条件时，则整个消毒区域能达到全覆盖。

传统的路径规划算法并不能保证全区域的杀毒，虽然使用移动式机器人可克服部分环境的限制，但仍面临着杀毒区域不够全面，包括由障碍物造成的小范围死角和杀毒点位不够精准的问题。此外，需考虑移动机器人电力不足，须返回充电站进行充电任务。为了解决上述问题，本研究提出了一种启发式自优化的路径规划（Heuristic Self-optimizing Path Planning，HSPP）算法。该算法旨在实现消毒区域的全覆盖，优化机器人的路径长度并确保回到起点。HSPP 分为2 个程序：路径生成与路径优化程序。在路径生成程序中，机器人试图基于SCAN 算法，生成一种路径的可行解，能够覆盖全区域的消毒轨迹。在路径优化程序中，采用贪心策略优化机器人的移动路径轨迹，减少机器人重复的移动轨迹。本研究的贡献有以下3 点：

（1）提出了HSPP 算法，设计并实现了路径生成与路径优化程序用于移动式紫外线消毒机器人。

（2）在路径生成程序中，HSPP 基于SCAN算法，达到全区域覆盖的目标，实现全区域消毒任务。

（3）通过路径优化程序寻求最小环的策略缩短机器人的总移动路径长度，提高消毒效率。

2 相关研究

国内外学者针对移动机器人的路径规划做了大量相关研究。Liu 等[2]提出一种基于Delaunay的测量算法，通过标定Voronoi 节点作为改进的A*算法寻路节点，并融合了动态融合寻路算法，提高了路径规划算法效率，但并未充分考虑路径规划中的全覆盖及安全性等。Hou 等[3]提出了一种基于蚁群算法的修正策略，能够减少移动路径中曲折路线信息造成的干扰，该方法能提升算法收敛速度和结果。王豪等[4]提出一种改进自适应遗传算法应用于机器人路径规划，将移动路径长度和拐点数量选为评估指标，并设计了自适应交叉算子等，提高了算法收敛速度等问题。陆向龙等[5]针对复杂的果园环境，提出了一种融合A*算法与DWA 算法路径规划算法，可实现果园复杂环境下喷雾机器人的作业需求。刘子豪等[6]针对室内移动中存在过多的冗余拐点等现象，提出一种改进的A*算法，结合跳跃点搜索理论,通过选取特定关键点的方法用于室内环境的机器人移动，结果表明在相同环境下，运行时间及总长度等均有明显的提高。秦涛等[7]设计一款集成紫外线消毒及喷雾功能的移动消毒防疫机器人，通过移动底盘进行地图构建和自主导航，能够在仿真地图环境下自主导航，可实现室内空间区域地面及较高位置消毒的需求。徐建萍等[8]设计一款可移动自动消杀机械控制系统，该机器人可携带不同的机械臂，通过即时定位与地图构建（Simultaneous Localization and Mapping，SLAM）技术进行导航操作，可满足对狭窄空间等进行无接触自动消杀作业需求。

3 紫外线消毒机器人路径规划

3.1 问题概述

为了实现对公共环境区域消毒的效果，可通过紫外线照射的方式，破坏和改变病毒微生物的结构，使病毒立即死亡或无法增殖，从而实现对环境消毒的目标。不妨通过设定待消毒的环境区域，按照前面所述，将整个环境区域（图1）切割成多个小网格，其中LG为小网格的大小，为紫外线照射半径。通过勾股定理，能够很容易得出网格长度LG与的关系式，如式（1）所示：

图1 紫外线照射半径与网格大小的关系

因此，机器人在小网格的中心位置，即代表该网格被机器人的紫外线所覆盖。本研究期望机器人在移动中以以最短路径遍历所有的小网格，确保每个小网格仅被访问一次，并最终返回到出发点，在这个设计中，借鉴了扫地机器人回到原点充电的思路[9]。此外，基于分治法的原理，通过遍历所有小区域的方式，当每个小区域都能被覆盖到，则整个区域都实现全覆盖的目标。在路径移动的问题上，为了节能与省时，同时期望遍历的路径越短越好，这个问题可转化为商旅问题(Travelling Salesman Problem, TSP) 的一个实例。假设在环境中，存在个小网格，这些网格可用集合来表示，机器人从起点L0出发后，然后沿着移动路径逐一访问每个网格，确保每个网格都能够被遍历1 次，最终再回到起点L0，因此，机器人的遍历路径Z 可描述为式（2）所示：

其中式（3）受限于式（4）：

那么，机器人的移动轨迹的最短路径SP，可用式（5）表示：

为了满足HSPP 中的路径生成与路径优化程序，机器人必须记录的每一个小网格的相关属性。假设整个区域Area 被切割成n 个网格，每一个网格gi∈Area，1 ﹤i ﹤n 都有唯一的ID、机器人网格的遍历路径满足，它们负责记录机器人需遍历网格的顺序。同时将区域的左上角网格g1设置为起点，机器人会遍历所有的网格，最终再回到起点g1。在机器人移动中，定义网格权值Wi用于记录网格g1被走访的次数，若某一个网格被机器人访问过多次，则权重值Wi越高，其初始值设置为0。另外，在遍历路径Z中设置标签ti标记，当tagi=1 代表可被删除，当tagi=0 代表不能被删除。

3.2 路径生成程序

设定机器人具有上下左右及其45°方向等8种移动方向，如图2 所示。

图2 机器人移动的8 个方向

HSPP 的路径生成程序是基于SCAN 产生移动网格路径轨迹（图3），并记录该网格的ID、遍历的次序及权值。假定机器人从左上角的网格中心点出发，沿着X 轴遍历每一个小网格，当同一行的网格都被遍历过后，沿着Y 轴向下移动一个小网格的距离，继续沿着X 轴的反方向遍历，直到遍历过所有网格，实现特定区域的全覆盖。在真实的环境中，机器人需避开移动路径上的障碍物。为此采用一种简单而有效的策略来绕过障碍物，即在机器人上安装激光雷达，让机器人在遇到障碍物时能够自主灵活地调整路径进行绕行。如图4 所示，当探测到左侧障碍物面积大于右侧时，机器人将向右侧的网格遍历，并沿着障碍物周围的网格绕行，反之则相反；如果障碍物太大，机器人无法判定左右两边面积的大小时，机器人随机选择一个方向的网格遍历并绕过障碍物。

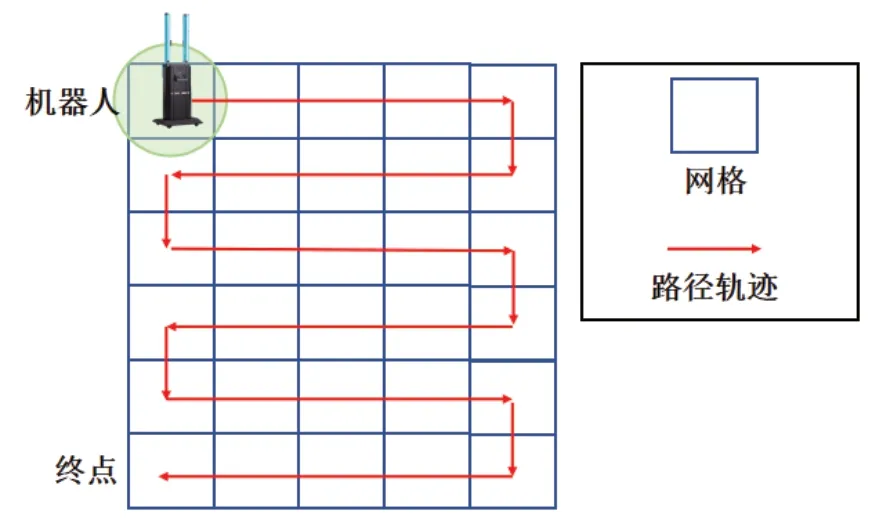
图3 机器人SCAN 的路径轨迹

图4 机器人遇障碍物绕行策略

3.3 路径优化程序

由路径生成程序生成的路径有时可能导致机器人在绕过障碍物时遍历了冗余重复路径，本研究要设法去除多余的路径，因此被访问超过1 次的节点必须去除。除此之外，去除的原则必须保证机器人的路径是不间断的。由于简单的SCAN并不总能生成一个最小环，为了避免过长重复路径，在路径生成程序执行后，启动路径优化程序。路径优化程序采用贪心法的策略，试图缩短机器人的遍历的路径。假设某路径生成程序所生成的序列Z={gi, gi+1, gi+2, gi+3,…, gn, gi}，对应的权值为wi, 1 ≤i ≤n。由于机器人必须从原点出发，最终返回原点，故路径优化程序只需从序列第2 个节点开始依次检查，以下为路径优化程序的步骤：

步骤1：设置检查起点位置，逐一向后检查每一个节点的权值，若节点的权值大于1 且位置与的邻接距离大于1 时，则继续向后检查，式（6）为位置i 与位置j 的初始化。

定义邻接距离Adj 为2 个相邻的节点，即在序列中位置的距离之差，如式（7）所示。

步骤2：当某节点的权值为1 时且位置i 与j的邻接距离等于1 时, 则该节点设置为检查终止位置j。删除起点位置i 与终止位置j 之间的节点。由于权值大于1 则代表该节点被遍历超过1 次，因此，可以删去权值大于1 的节点。假设原始序列Z 中，元素个数有n 个，SS 为位置i+1 至位置j-1的元素所构成的集合，元素有m 个，因此可以表示为式（8）：

步骤3：由于将权值大于1 的删除，所以权值wk必须减1（更新）成为新的权值，如式（9）所示。

步骤4：若尚未达到序列的最后节点，则将终止位置设置为新的起点位置并返回第1 步，否则整个程序结束。以图5 为例，在序列中增加许多重复路径，以此证明如何通过优化路径程序来优化路径长度。假设路径轨迹Z(0)={g1, g2, g3, g6,g5, g4, g7, g8, g9, g8, g5, g6, g3, g2, g1}，序列长度为15。由于序列头尾节点是不能够被删除的节点，故先将检查起点位置设置为第2 个节点g2，由第二个结点逐步向后检查，发现到第6 个节点g4与第2 个节点相邻（相邻距离为1），同时第6 个节点的权值为1，因此将第6 个节点设置为检查终止位置j。因此，能够将节点g3、g6和g5删除。紧接着，将检查起点位置i 设为j，再将设置为新的检查起点,逐步向后检查。直到第9 个节点为i，第11 个节点为j 时，其第10 个节点g8符合被删除的条件，因此将第14 个节点删除。经过优化程序后的结果为Z(1)={g1, g2, g4, g7, g8, g9, g5, g6, g3, g2,g1}，如表1 所示。接着再将优化过1 轮的序列整理后继续进入第2 轮的路径优化程序。从序列Z(1)中，发现Z(1)已无法再优化，故路径优化程序结束。

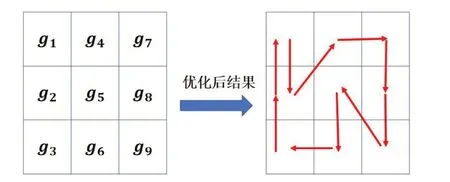
图5 机器人经路径程序优化后的路径长度示例

表1 经过一轮路径优化程序案例

4 仿真实验设计及结果

4.1 实验环境与参数设置

在仿真开发方面，使用Windows 10 系统，利用Java 语言、MATLAB 以及Gnuplot 作为绘图及辅助工具。通过设定3 组对比实验来比较HSPP、随机法和SCAN 的平均路径长度比和平均覆盖率等内容。

随机法要达到全覆盖需花费很长的时间，假设机器人移动1 个小网格耗费1 个单位时间，S定义为总路径长度与2 倍的网格总数的比率，其中Atotal为整个区域的网格总数，而平均路径长度APL 等于SPLR 除以总执行次数，如式（10）所示：

当遍历序列S 中的网格Gj与Gk存在路径时，xij为1 否则为0，其中exe 为总执行的次数。此外，为了评估紫外线消毒机器人的消毒效率并实现全区覆盖的目标，定义Acovered为被覆盖的网格总数，那么覆盖率的计算方式如式（11），平均覆盖率CR 可用式（12）表示：

每组实验进行如下：（A）改变区域大小；（B）改变障碍物数量；（C）改变障碍物大小。实验设置的参数见表2。

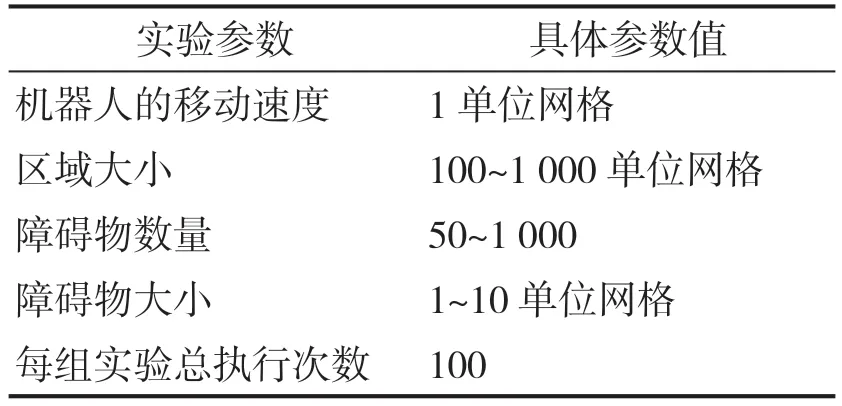
表2 实验参数设置

4.2 改变区域大小的影响

在本实验中，通过改变区域的大小，比较3 种方法的平均路径长度与覆盖率的效能。其中区域边长从100 单位网格数递增至500 单位网格数，每组实验的区域边长每次递增50 个单位网格，障碍物的大小为1 个单位网格，障碍物的数量固定为1 500 个。从图6 可看出，区域大小的改变对于HSPP 与SCAN 法在覆盖率上并无明显区别，原因在于SCAN 是以全区域覆盖目标所设计，HSPP 的路径生成程序是基于SCAN 改进的。在平均路径长度比表现方面，SCAN 的路径长度约为随机法的0.6 倍，而HSPP 约为随机法的0.4 倍，效果最佳。这是由于随机算法未考虑到覆盖与路径的问题，SCAN虽考虑了移动路径，但当环境中存在较多障碍物时，SCAN 未对路径进行优化，会生成许多重复的路径；而HSPP 考虑了重复路径问题，针对路径长度进行了优化。

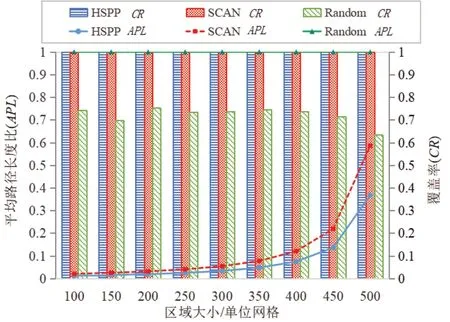
图6 区域大小对路径长度的影响

4.3 改变障碍物数量的影响

在本实验中，设法改变障碍物的数量，比较3 种方法的平均路径长度比与覆盖率的效能。区域的大小固定为单位网格，障碍物的大小固定为1 个单位网格，随机生成的障碍物数量从600 个递增至1 500 个，每组实验的障碍物数量依次递增100 个。从图7 可看出，障碍物数量的改变对于HSPP 与SCAN 法的覆盖率有一定影响。当障碍物数量达到1 500 个，HSPP 的平均路径长度比为0.36，SCAN 的平均路径长度比为0.58。随着障碍物数量的增加，SCAN 的重复路径增加，HSPP 使用优化程序进行优化，使得其平均路径长度比明显优于SCAN 与随机法。

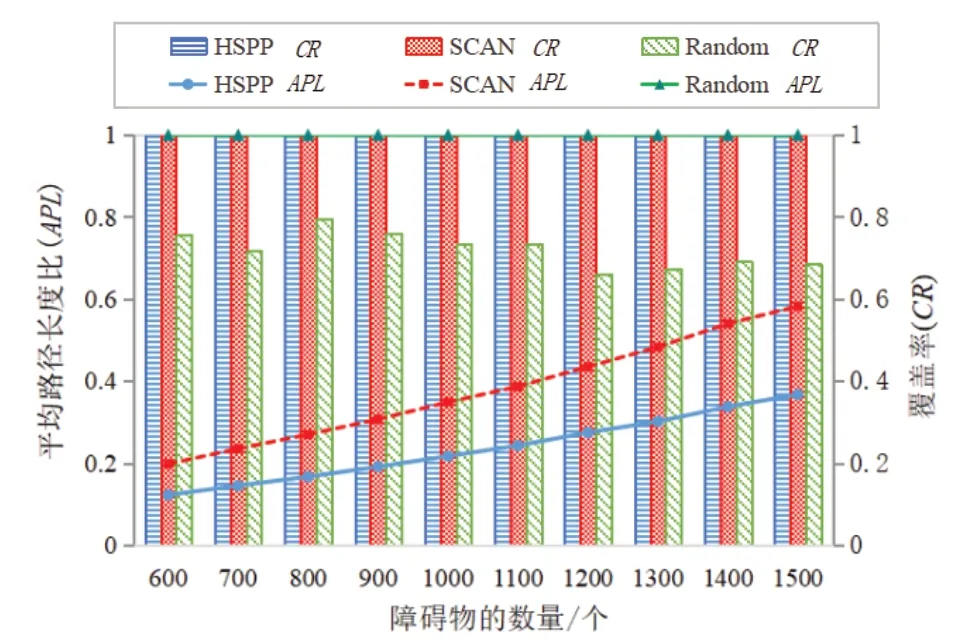
图7 障碍物的数量对路径长度的影响

4.4 改变障碍物大小的影响

为了营造不规则区域场景的环境，在实验中，通过改变障碍物的大小，形成各种不同形状大小的障碍物，并使得障碍物间可能相邻。本组实验同样比较3 种方法的平均路径长度比与覆盖率的效能。区域的大小固定为 单位网格，障碍物的数量固定为500 个，障碍物的大小从1 个单位网格大小递增至10 个单位网格大小，每组实验的障碍物的大小递增1 个单位网格。从图8 可看出，障碍物大小的改变对于HSPP 与SCAN 法的覆盖率都达到100%。当障碍物大小为10 时，HSPP 的平均路径长度比为0.363，SCAN 的平均路径长度比为0.41。随着障碍物大小的增加，SCAN 的重复路径随之增加，经过优化程序的HSPP 算法在平均路径长度比明显优于随机法，且比SCAN 表现更好。

图8 障碍物的大小对路径长度的影响

5 结论

移动式紫外线杀毒机器人是一种高效且实用的公共环境消毒技术应用，但现实中移动机器人未能完全满足复杂环境区域的任务需求，常因移动轨迹未优化、消毒区域不全面等问题而未能发挥出最大效能。而在本研究中装载HSPP 算法的移动式紫外线消毒机器人能够通过SCAN 生成一种可行的移动轨迹进而优化的方法，能很好地满足全区域高效全面的消毒任务，具有很好的应用价值。