另辟蹊径 化难为易

◎赖晓宇

题目：有一个正方形（如图1），它的面积是8平方米，这个正方形内切一个最大的圆，这个最大的圆面积是多少平方米？

图1

分析：按常规的思考，要求正方形内切圆的面积，需要先求出圆的半径。而正方形内最大圆的直径等于正方形的边长，因为正方形面积是8 平方米，8 是由哪两个相等的数相乘得到的呢？这个问题在小学数学中很难解决。但如果我们另辟蹊径转换思路，问题就可以化难为易。

解法一：把正方形面积缩小一半为4 平方米，因为2×2=4，所以缩小后的正方形边长为2 米，也就是缩小后圆的直径为2 米，即半径为1 米，这样缩小后圆的面积是3.14×1×1=3.14（平方米），原来这个圆的面积是3.14×2=6.28（平方米）。

解法二：把正方形面积扩大2 倍为16 平方米，因为4×4=16，所以扩大后的正方形边长为4 米，也就是扩大后圆的直径为4 米，即半径为2 米，这样扩大后圆的面积是3.14×2×2=12.56（平方米），原来这个圆的面积为12.56÷2=6.28（平方米）。

解法三：在图中画出两条互相垂直的半径（如图2），这样把正方形平均分成了四个小正方形，小正方形的面积就是r2，所以圆的面积是=（平方米）。

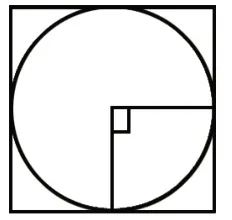
图2

解法四：由于圆的面积和正方形的面积之间的关系为：，也就是圆的面积是正方形的面积的，所以，圆的面积是（平方米）。