基于超图的多尺度决策信息系统最优尺度选择
马周明, 黄 闽, 林国平, 施虹艺
(1.闽南师范大学数学与统计学院,福建 漳州 363000;2.闽南师范大学福建省粒计算及其应用重点实验室,福建 漳州 363000)
Pawlak[1]于1982年提出了经典粗糙集理论,随着数据挖掘等信息技术的迅速发展,经典粗糙集理论现已被广泛用于处理不确定数据及特征选择问题,成为分析处理不精确、不一致、不完整等不完备信息的有效工具.基于经典粗糙集理论,众多学者提出了优势粗糙集[2]、邻域粗糙集[3-6]等广义粗糙集模型.
Lin[7]在1998年首次提出“粒计算”概念.粒计算作为一种处理多尺度数据的方法,注重在各种粒度层面上进行数据处理.采用这种多粒度视角,粗糙集理论在处理多尺度或分层信息时的效率得以显著提升,尤其是在特征选择和数据分类等方面.这种多层次的数据处理方法在医疗诊断、图像识别、决策支持系统等多个领域中得到应用,并展示了其在处理模糊、不确定或不完整信息方面的强大能力.将粒计算理念融入到粗糙集理论中,诸如多粒度粗糙集[8-10]这样的模型便得以诞生.这类模型通过考虑不同粒度层次上的知识,为分析复杂信息系统提供了新的视角.而现实世界的应用场景复杂多变,一个样本在某特定特征上可能存在多个不同等级的评价尺度.针对这一问题,Wu 等[11]提出了Wu-leung 多尺度信息系统模型.对于寻找多尺度决策信息系统中尺度的变化规律与最优尺度选择,Chen 等[12-13]利用三支决策研究目标动态增长条件下局部最优尺度的更新规律.在保持系统的不确定域不变的情况下,首先探讨了对象增量情况下决策信息系统中决策类的不确定性更新规律.其次,利用序列三向决策理论给出了保持决策类不确定性的局部最优尺度的定义,并利用决策类不确定性的更新机制给出了最优尺度的更新规律.Li 等[14]利用三支决策中的不确定域,探讨了最优尺度变大或者不变的充要条件.Yang 等[15]提出了一种新的成本敏感多粒度S3WD 模型,对于S3WDRFS 及其三个区域,以层次颗粒结构揭示了其决策代价的变化规律,通过考虑用户的需求,讨论如何实现目标优化机制与总成本最低的最优粒度.Hao等[16]应用序贯三支决策理论研究了该系统中决策类别的不确定性与尺度变化之间的关系,提出了不确定性的最优尺度选择,并给出了添加新对象时的更新规律.目前大部分研究集中在如何选取多尺度决策信息系统的最优尺度组合[17-21].
图论中求解极小顶点覆盖问题为一个NP-hard问题,长期以来,许多学者对该课题从不同层面或不同角度的进行了探索和研究.Chavatal[22]在1979 年提出了经典的顶点覆盖算法.Chen 等[23]研究了特征子集选择与极小顶点覆盖之间的关系,发现求图的极小顶点覆盖等价于求信息系统的特征子集选择.同时,特征子集选择亦可转化为图的极小顶点覆盖的计算.Mi等[24]利用图论的相关理论方法,对基于区分矩阵的粗糙集特征选择方法给出了直观和等价的刻画.Zhang 等[25]利用图的思想研究了覆盖决策信息系统特征子集选择算法,首先计算覆盖决策信息系统的辨识集,进而得到一个超图的关联矩阵.然后,基于贪心法求该超图的极小顶点覆盖,该方法可以看作是一种局部逼近最优的特征子集选择策略.Jin 等[26]通过构造多尺度辨识矩阵,将辨识矩阵与多尺度信息系统结合,探究其特征选择与最优尺度选择.
目前已有研究中的多尺度决策信息系统的特征选择与最优尺度选择算法,在面对高维尺度以及海量样本时具有较高的时间复杂度以及时常陷入局部最优解.利用图论解决该问题的传统方法中,边的数目繁多且不直观,不利于获取极小顶点覆盖.将超图与多尺度信息系统结合,控制特征邻接关系数目,利用超图对多尺度信息系统中特征的邻接关系可视化,提出了基于超图的多尺度信息系统最优尺度特征求解算法,在处理高维度数据时具有显著的优势.
1 预备知识
本节介绍关于多尺度决策信息系统中的基本知识.
定义1[27]设S=(U,C)为一个信息系统,U是非空有限论域,C为特征集.对于任意特征a∈C,称a:U→Va是信息函数,Va称为特征a的值域.
定义2[20]设S=(U,C) 为一个信息系统,C为特征集 对B⊆C且B≠∅,有不可辨识关系RB={(xi,xj)∈U|∀b∈B(b(xi)=b(xj))}.显然RB为U上的等价关系.论域U被RB划分为两两不相交的等价类U/RB={[xi]B|x∈U},其中
设X为U的任意非空子集,定义X关于特征子集B的上近似和下近似为
定义3[20]设S=(U,C∪D)为一个决策信息系统,D为决策特征类,由∀d∈D诱导的不可辨识关系Rd,若RC⊆RD,则称该决策信息系统S是协调的,否则称决策信息系统S是不协调的.
定义4[20]设S=(U,C∪D)为一个协调决策信息系统,设B⊆C,称B为协调决策信息系统S的一个特征选择子集,若B满足
1) [xi]B⊆[xi]D,∀xi∈U;
2)∀a∈B,∃x∈U,[xi]B-{a}≠[xi]B.
定义5[10]设S=(U,C∪D)为一个协调决策信息系统,假设C中的每个特征都具有I个等级的尺度,决策类D为单一等级的尺度,则多尺度决策信息系统可以表示为
对于1≤t≤l,存在映射,即,其中为粒度信息转换函数.
性质1[17]设S=(U,C∪D)为一个协调多尺度决策信息系统,其中B为C的一个特征子集,xi,xj∈U,对∀at∈B,t∈[1,2,···,I],满足
1)RBt={(xi,xj)∈U×U|at(xi)=at(xj)};
2)[xi]Bt={xj∈U|(xi,xj)∈RBt}={xj∈U|at(xi)=at(xj)};
3)U/RBt={[xi]Bt}.
则有RB1⊆RB2⊆…⊆RBI,[xi]B1⊆[xi]B2⊆…⊆[xi]BI.
定义6[21]设S=(U,C∪D)为一个广义多尺度决策信息系统,对于特征am∈C,取第lm等级的尺度,m=1,2,…,n.定义指标序列K=(l1,l2,…,ln),有,SK=(U,CK∪D),则称K为SK在S中的一个尺度组合,记所有的尺度组合为κ.
定义7[21]设S=(U,C∪D) 为一个协调多尺度决策信息系统,κ是S的所有尺度组合,对K1=(l11,l12,…,l1n),K2=(l21,l22,…,l2n)∈κ,若对于m=1,2,…,n均有l1m≤l2m,则称尺度组合K1细于K2,记作K1-≺K2.
进一步地,若K1≺-K2且∃p∈{1,2,…,n},使得lp1<lp2,则称尺度组合K1严格细于K2,记作K1≺K2.
性质2[21]设S=(U,C∪D)为一个协调多尺度决策信息系统,尺度组合K1=(l11,l12,…,l1n),K2=(l21,l22,…,l2n)∈κ,有
其中:lj=min{l1j,l2j},Lj=max{l1j,l2j},j=1,2,…,n.
定义8[28,30]给定一个协调多尺度决策信息系统S=(U,C∪D),对∀xi,xj∈U,定义|U| ×|U|的矩阵M为S的辨识矩阵,其中
对于协调多尺度决策信息系统S=(U,C∪D)的其辨识矩阵M,其辨识函数定义为
其中:∨M(xi,xj)表示辨识矩阵M中所有辨识集的析取;∧M(xi,xj)表示辨识矩阵M中所有辨识集的合取.
性质3[29-30]设S=(U,C∪D)为一个协调多尺度决策信息系统,B⊆C是S的一个特征子集当且仅当是fM的主蕴含项.
2 多尺度决策信息系统特征邻接关系及其诱导的超图
本节定义了β邻域,用样本间的距离构造了极小相似对,生成特征间的邻接关系,利用超图将其可视化.探究求解信息系统中的特征子集选择与对应超图的极小顶点覆盖问题间的关系.
受到文献[31]的启发,类似地定义样本关于特征的邻域.
定义9设S=(U,C∪D)为一个协调多尺度决策信息系统,对am∈C,xi∈U,给定阈值β∈[0,1],若有xj∈U,使得d(xi)=d(xj)或|atm(xi)-atm(xj)| <β,t=1,2,…,I,称xj在xi关于特征am的β邻域中.记(xi)为xi关于特征am的β邻域,其中
定义10设S=(U,C∪D)为一个协调多尺度决策信息系统,am∈C,xi∈U,给定阈值β∈[0,1],若有xj∈U,使得d(xi)≠d(xj)且,则xj在xi关于特征am的β邻域的补集之中.记为xi关于特征am的β邻域补集,其中
其中t=1,2,…,I,β为给定的阈值.因,故(xi)为xi的一个去心领域.
性质4设S=(U,C∪D)为一个协调多尺度决策信息系统,其中Nβam(xi)为xi关于特征am的β邻域,(xi)为xi关于特征am的β邻域补集,有
定义11设S=(U,C∪D)为一个协调多尺度决策信息系统,(xi)为xi关于特征atm的β邻域补集,对∀xj∈(xi),定义(xi,xj)为xi关于特征am的相似对,记特征am的所有相似对为δ(am).
对于(xi,xq)∈δ(am),若不存在(xi,xp)∈δ(am),使d(xi,xp)<d(xi,xq),那么称(xi,xp)为特征am下的极小相似对,记为δmin(am).其中
定义12[22]设G=(V,E)为超图,V代表包含对象的集合,E为基于V构建的超边ei的集合.在传统图结构中,它的一个边只能和两个顶点连接,若边的端点重合为一个顶点,则称为环.超图是在传统图上的泛化.在超图中,每条边可以连接任意数量的顶点,记边ei中的顶点集为N(ei).
定义13[32]给定图G=(V,E),对于V'⊆V,若V'中的顶点能覆盖图G所有边,那么称V'为图G的一个支配集.若V'为图G的一个支配集,对∀v∈B,若V'-{v}不能覆盖图G的所有边,那么称支配集V'为图G的一个极小顶点覆盖.
性质5[23,32]给定图G=(V,E),v∈V'⊆V,若V'是图G的极小顶点覆盖当且仅当是fG的一个主蕴含项,其中
定义14设S=(U,C∪D)为一个协调多尺度决策信息系统,记R(C)={R(a1),R(a2),…,R(an)}为C的特征组合集,其中am∈C,δmin(am)=(xi,xj),有R(am)={atk||atk(xi)-atk(xj) |≥β}.
受到文献[23]的启发,根据定义14 得到的特征间邻接关系R(C),类似地定义多尺度决策信息系统诱导的邻接矩阵.
定义15设S=(U,C∪D)为一个协调多尺度决策信息系统,对于atk∈C,k∈{1,2,…,m},t∈{1,2,…,I},定义|m| ×|m×I|的矩阵Is为多尺度决策信息系统诱导的邻接矩阵,即
Is(am,atk)代表的位置为矩阵Is的第m行,第((k-1)×I+t)列.
令e∈R(C),表示e为R(C)中的元素,记V=C,E={e∈R(C)}.称GS=(V,E)为协调多尺度决策信息系统S的所生成的超图.
由定义15 可知,超图GS实际上是协调多尺度决策信息系统S的特征作为顶点集,以邻接关系作为边集,是特征间的邻接关系的直接刻画.根据性质3 和性质5,可知通过邻接矩阵生成的超图的极小顶点覆盖与该决策信息系统S的特征选择子集是相同的[23-24,33].故求决策信息系统的特征选择问题亦可转化为求相应图的极小顶点覆盖问题.
例1设S=(U,C∪D)为给定的协调多尺度决策信息系统,U={x1,x2,…,x6},D={0,1},特征类C={al1,al2,al3},其中l=1,2,3,β=0.5,详见表1.
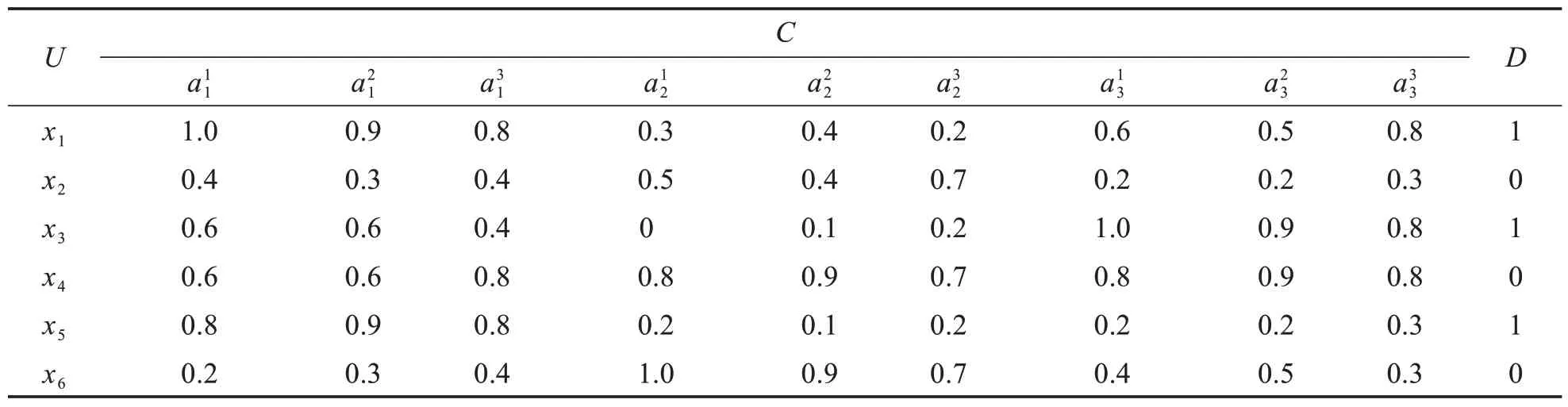
表1 协调多尺度决策信息系统Tab.1 Generalized coordination multi-scale decision information systems
对于协调多尺度决策信息系统S,计算可得所有相似对为
根据式(9),计算得到特征下的极小相似对δmin(a1)=(x2,x5),δmin(a2)=(x2,x5),δmin(a4)=(x2,x3).计算极小相似对中的特征间邻接关系,可得R(a1)={a21,a32},R(a2)={a21,a32},R(a3)={a12,a32,a13,a23}.令V=C,E=R(C),得到表2 所示的邻接矩阵,用超图将其可视化,如图1 中的超图G所示.由于v11,v31,v22,v33并未出现在任一边中,与其他顶点均未连接,不另外表出.根据式(10)可得
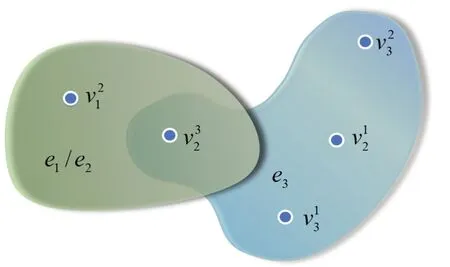
图1 邻接矩阵诱导的超图Fig.1 Hypergraph induced by adjacency matrix

表2 多尺度决策信息系统诱导的邻接矩阵Tab.2 Adjacency matrix induced by multi-scale decision information systems
由此可得图超图G的极小顶点覆盖有{v32},{v21,v12},{v21,v13},{v21,v23}.令V=C,可得{a32},{a21,a12},{a21,a13},{a21,a23}为协调多尺度决策信息系统S的尺度特征选择子集.
根据布尔函数求解超图的极小顶点覆盖,在顶点数相同或是极小顶点覆盖中尺度相近,往往无法明确得到一个最优解,接下去探究对超图中顶点的提取规则,以得到极小顶点覆盖的最优解.
3 基于超图的多尺度决策信息系统最优尺度特征选择
目前关于多尺度决策信息系统的最优尺度组合算法,在处理高维度样本时效率不高且易陷入局部最优,而利用图论解决该问题的传统方法中,边数目繁多复杂,两者都影响了数据挖掘效率.针对这些问题提出基于超图的多尺度决策信息系统最优尺度特征求解算法.
定义16设S=(U,C∪D)为一个协调多尺度决策信息系统,对∀R(am)≠φ,∃atm∈R(am)使得Ram-{}=φ,则称R(am)为核心子集.定义core(C)为核心特征集.若atm∈core(C),称为核心特征.
定义17设S=(U,C∪D)为一个协调多尺度决策信息系统,R(C)为特征间的邻接关系,对∀atm∈R(am),R(am)≠{},有
1)当core(C)∩R(am)≠∅,称R(am)为不必要子集,记Run(C)为全体不必要子集;
2)当core(C)∩R(am)=∅,称R(am)为必要子集,记Rne(C)为全体必要子集,∩Rne(C)为所有必要子集的交.
定义18设S=(U,C∪D)为一个协调多尺度决策信息系统,对第k个特征,有atk∉core(C),且∩Rne(C)={apk},那么apk为特征选择子集中的必要特征.对apk,aqk∈∩Rne(C),若q<p,那么apk为特征选择子集中的必要特征,为特征选择子集中的不必要特征.
性质6设S=(U,C∪D)为一个协调多尺度决策信息系统,对第k个特征,有atk∉core(C),且∈∩Rne(C).apk为特征选择子集中的不必要特征当且仅当∃aqk∈∩Rne(C),且p<q.
证明首先证明其必要性.因apk为特征选择子集中的不必要特征,则有apk∈∩Rne(C).若不存在∈∩Rne(C),其中aqk∈C且p<q,那么apk为特征选择子集中的必要特征.这与apk为特征选择子集中的不必要特征所矛盾,可得∃apk∈∩Rne(C).
其次证明充分性,当apk,aqk∈∩Rne(C),且p<q,由定义18可得apk为不必要特征.
定义19设S=(U,C∪D)为一个协调多尺度决策信息系统,∀ak∈C∧ak∉core(C),记当前必要子集数目|Rne(C)| =γC.定义∂(alk)为alk的特征权重,其中
令E=R(C),V=C.对∀vi,vj∈V,若∂(vi)>∂(vj),有vi▷vj,定义“▷”为顶点优先序.当∂(vpi)=∂(vqi),若p<q,则vqi▷vpi.进一步地,为了减少极小顶点覆盖的搜索成本,若vqi为必要特征,则令vri=0,其中r<q.
当记max ∂(v)为当前顶点优先序下的首位顶点.核心顶点集不能覆盖所有的边时,依照优先序,添加max ∂(v)至极小顶点覆盖中.若max ∂(v)不唯一,则同时选取.
例2设S=(U,C∪D)为给定一个协调多尺度决策信息系统,其中U={x1,x2,…,x8},决策类D={0,1},特征类,l=1,2,3,给定β=0.5,详见表3.
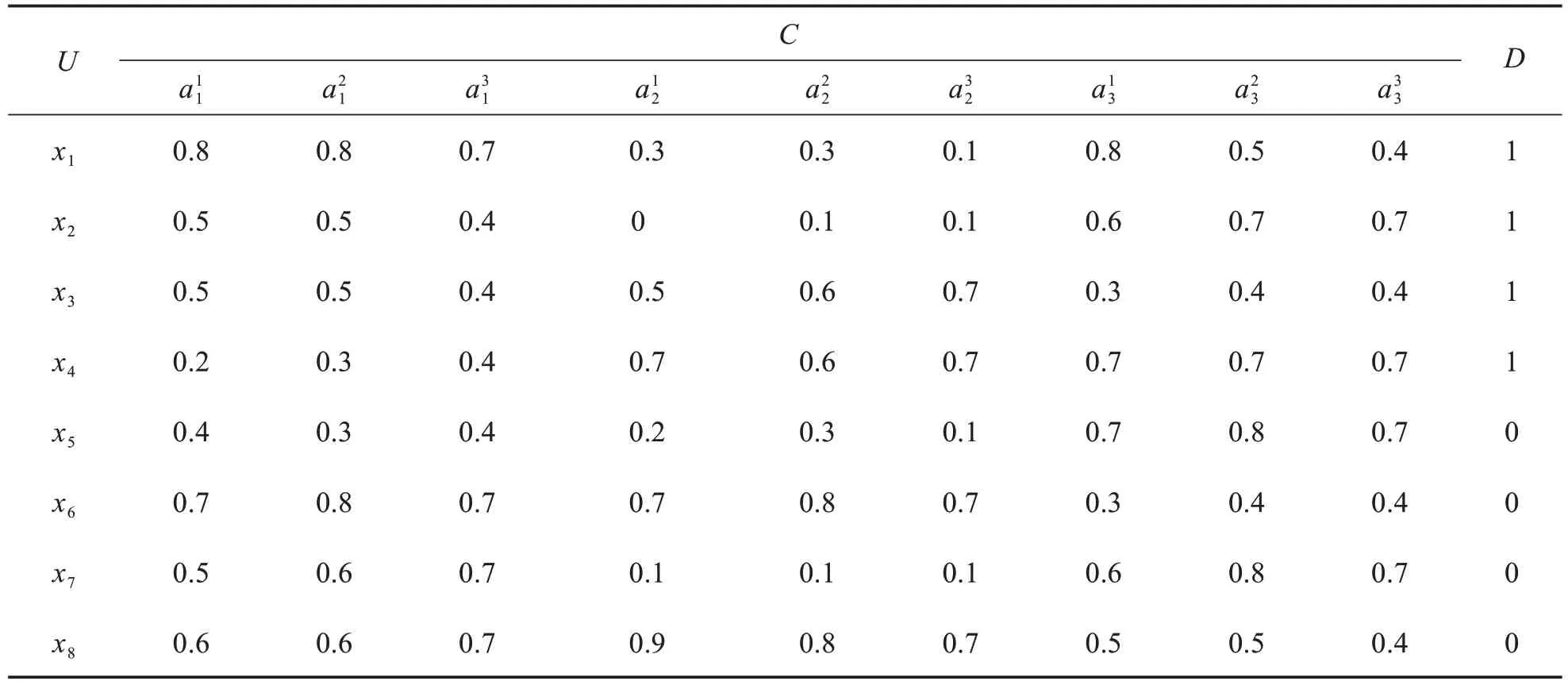
表3 协调多尺度决策信息系统Tab.3 Generalized coordinated multi-scale decision information systems
根据定义11可得每个特征的相似对为
由此可得到每个特征下的极小相似对
计算极小相似对中的特征间邻接关系,可得
令E=V,得到如表4所示的多尺度决策信息系统诱导的邻接矩阵.用超图将其可视化,如图2所示.
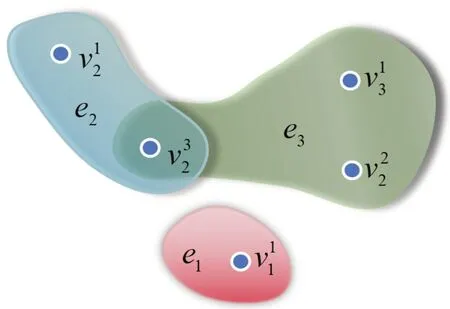
图2 邻接矩阵诱导的超图Fig.2 Hypergraph induced by adjacency matrix

表4 多尺度决策信息系统诱导的邻接矩阵Tab.4 Adjacency matrix induced by multi-scale decision information systems
由于v21、v31、v23、v33并未出现在任一邻接关系中,故与其他顶点均无超边连接,不额外表出.N(e1)中只有一个顶点,core(V)={v11},去除v11所覆盖的边剩下的边为e2,e3,计算N(e2),N(e3)中顶点的权重,同时,对∀vt1,t∈l,令∂()=0.
计算可得∂(v12)=0.5,∂(v22)=0.5,∂(v32)=1,∂(v13)=0.5.计算顶点优先序,可得v32▷v13=v22=v12,此时max ∂(v)=v32,将v32添加到极小顶点覆盖集当中,删除被v32所覆盖的边,此时已无剩余边,令C=V,故{a11,a32}为协调多尺度决策信息系统S的一个特征选择子集.
根据例3的求解步骤,给出基于超图的多尺度决策信息系统最优尺度特征求解算法.

算法1 基于超图的最优尺度特征求解算法(MGED算法)输入:协调多尺度决策信息系统S=(U,C ∪D),alk:k ∈[1,n], l ∈[1,I],阈值β输出:最优尺度特征选择子集Cη 1:根据定义11得到δmin(a)2:生成R(ak),令V=C,E=R(C),Ene=Rne(C),将其刻画成超图Gs 3:for k=1:n 4: while |N(ek)|=1 5: core(V)←core(V)∪{vlk}6: while N(ek)∩core(V)=∅7: Ene ←Ene ∪ek 8:Cη←Cη∪core(V)9:while E ≠∅10: 计算∂(v),对∀vt m ∈Cη,令∂(vpm)=0,其中p=1,2,…,l.对∂(v)排序11: if max ∂(v)=vtm∧∀vpm ∩core(V)=∅12: Cη←Cη∪vt m 13: if vt m ∩N(ek)≠∅14: Ene ←Ene-ek 15: else 16: ∂(vpm)←0 17: end if 18: else 19: ∂(vpm)←0 20: end if 21:令C=V,输出Cη
MGED 算法在步骤1~2 中的时间复杂度为O(|U|*n*I),在步骤3~8 中时间复杂度仅为O(n).在步骤9~20中,仅有一层循环结构,该部分时间复杂度最为O(n!).因此,对于高维度数据集,MGED 算法能够有效提高特征选择的效率.
4 实验设计与分析
为了验证算法的有效性,对算法进行数值实验分析与对比.CDG 算法[34]、GBFS 算法[26]都是采用图论方法来对多尺度信息系统求解最优尺度组合.CDG 算法是在单尺度信息系统进行特征选择,采用辨识矩阵来刻画图的每一个边集;而GBFS 算法则是将其推广到协调多尺度决策信息系统.两种算法与MGED算法均具有一定的对比性.
实验选取了10个UCI上的公开数据集,数据集基本信息如表5所示.有高维数据集也有低维数据集.β取值均为0.5,每个数据集运行10次,取10次的平均成绩来对比分析各个算法的性能水平.
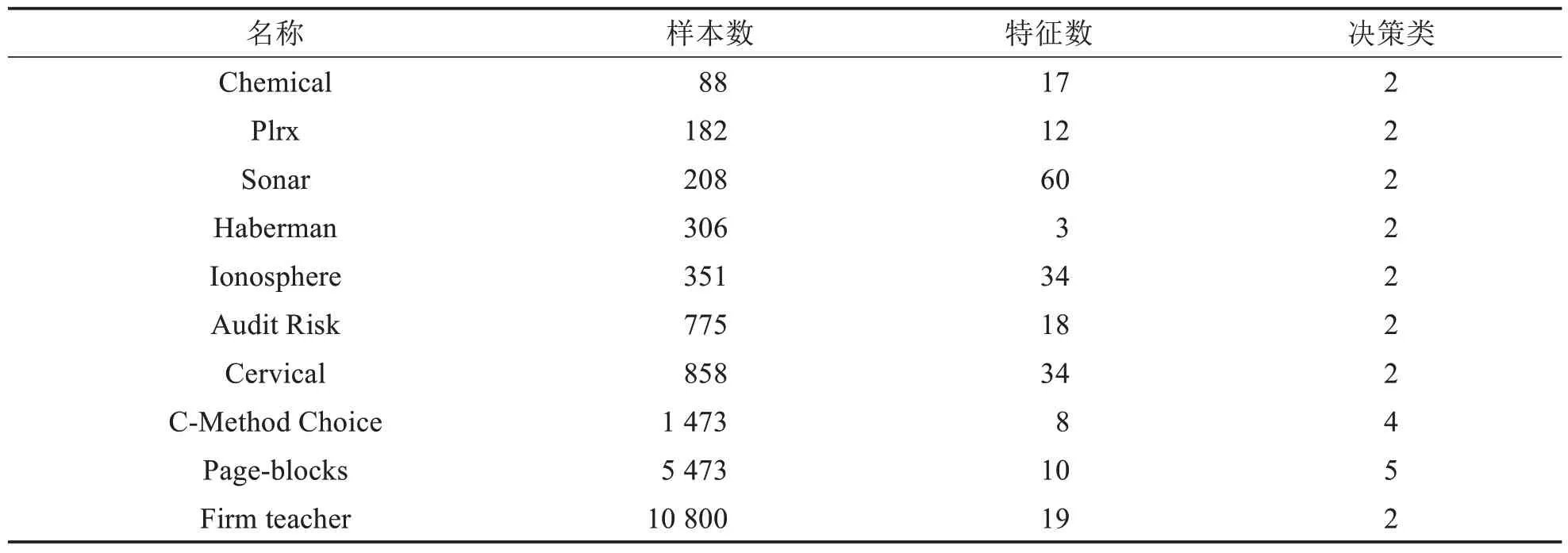
表5 数据集基本信息Tab.5 Basic information about the datasets
值得注意的是,UCI中的数据集均为单尺度数据集,因此先对这些数据集进行预处理.
1)删除具有缺失特征的样本.
2)将特征中的语义型数据转化为数值型数据.
3)利用类似合并相邻方法将单一尺度扩充成为多尺度.定义ϕσk(at)为特征a第t等级下的第k个特征相似域,其中σ为特征相似域的容量.
将原始尺度记为第1等级尺度,则有ϕσ1(a1m)为特征am在第1等级下的特征相似域,且特征相似域容量为σ1=1.将样本按am的特征值升序排列,设ϕσ2(a2m)为第2等级的特征相似域,其容量为σ2,且σ2>σ1.
将第1 等级尺度am下的每个特征值,按照顺序分配至对应的特征相似域中,并取每个特征相似域中平均值生成第2 尺度.即第1 至第σ2个特征值分配到第1 个特征相似域并取均值,第σ2+1 至第2σ2个特征值分配到
第2个特征相似域并取均值,以此类推,结果均保留两位小数.若最后一个特征相似域中特征值数目不足σ2,则在取均值时从前一个特征相似域中随机挑选对应数量的特征值加入计算.直至遍历完所有尺度特征.
设第3尺度等级的特征相似域为φσ3(a3),其中σ3>σ2,依照生成第2尺度方法,将第2尺度下的特征值分配至ϕσ3(a3),生成第3尺度.直到生成最后一个尺度.本次实验对所有数据集统一选取10个等级尺度,且σn=n.
文中的算法均在基于Python3.9的Spyder软件中实现,并在装有Windows 10的个人电脑上运行,电脑核心处理器为i5-10300H,四核心八线程,主频2.5 GHz,最大睿频4.5 GHz,运行内存为8 GB.
将每个数据集U平均分成10 个子集{U1,U2,…,U10}.将U1作为第一个临时数据集,即10%的样本,U1∪U2作为第二个临时数据集,样本比例为20%,以此类推.对于每个特征,均取十个等级的尺度.
MGED 算法与GBFS 算法对于各比例样本的时间差异,如图3 所示.可以看出,MGED 算法在大部分数据集上都具有一定的时间优势.在数据集维度较小时,MGED算法与GBFS算法差距并不十分明显.但从图的整体趋势来看,样本比例越大,两个算法的时间差异越明显.在100%的Ionosphere数据集与Cervical数据集中,MGED算法用时均不超过GBFS算法用时的4%.说明MGED算法在处理高维数据更具有优势.采用十折交叉法将两个算法在100%样本比例下所得的特征子集结果,在CART、LDA、SVM、KNN、SDA 与3N 分类器上进行其分类性能评估.其中原始尺度记为RAW,最粗的尺度记为COAST,添加文献[23]中的CED算法作为对比,对比结果如表6~11所示.
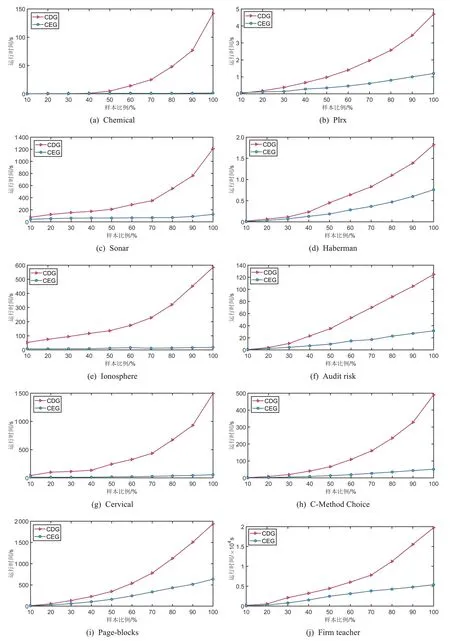
图3 不同样本比例下的时间变化Fig.3 Time variation at different parameter levels
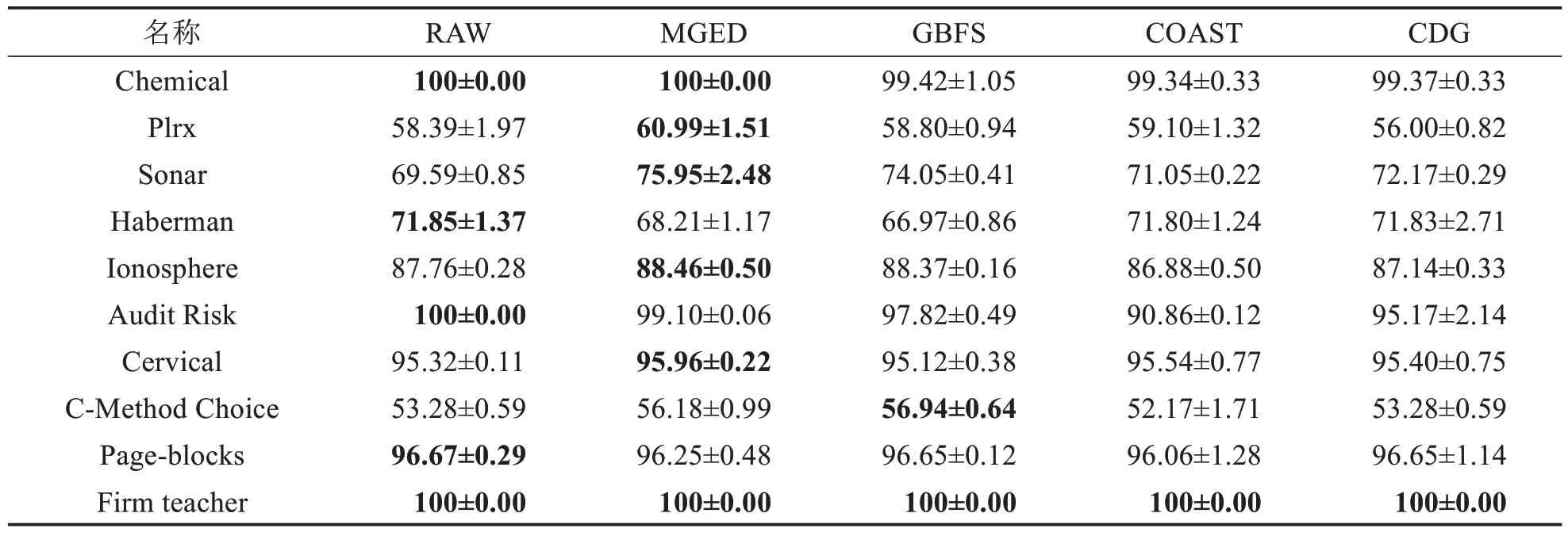
表6 CART分类器上的精度比较Tab.6 Accuracy comparison on classifier CART (单位: %)
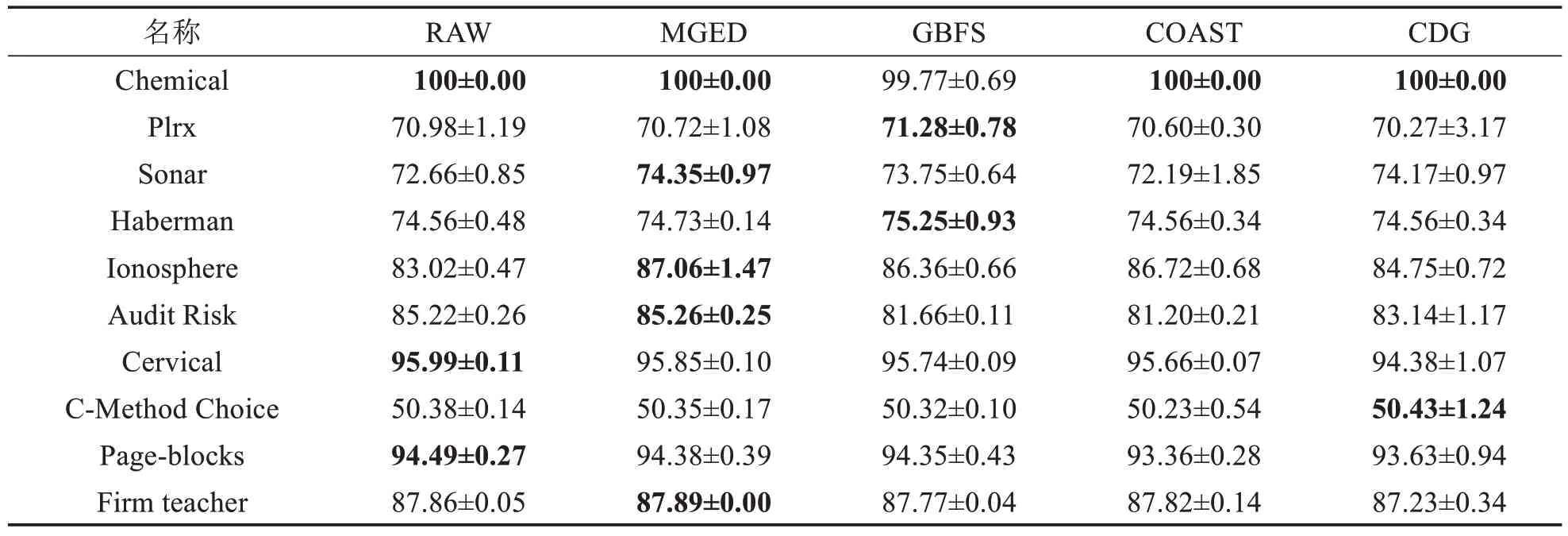
表7 LDA分类器上的精度比较Tab.7 Accuracy comparison on classifier LDA (单位: %)
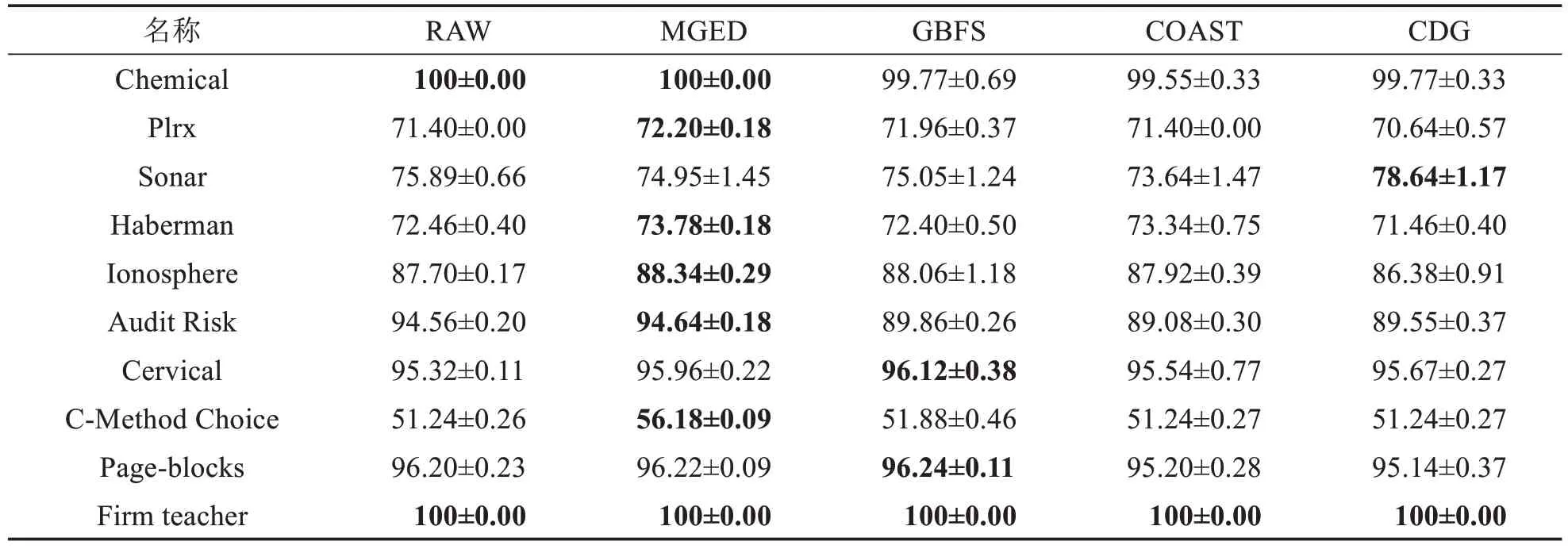
表8 SVM分类器上的精度比较Tab.8 Accuracy comparison on classifier SVM (单位: %)
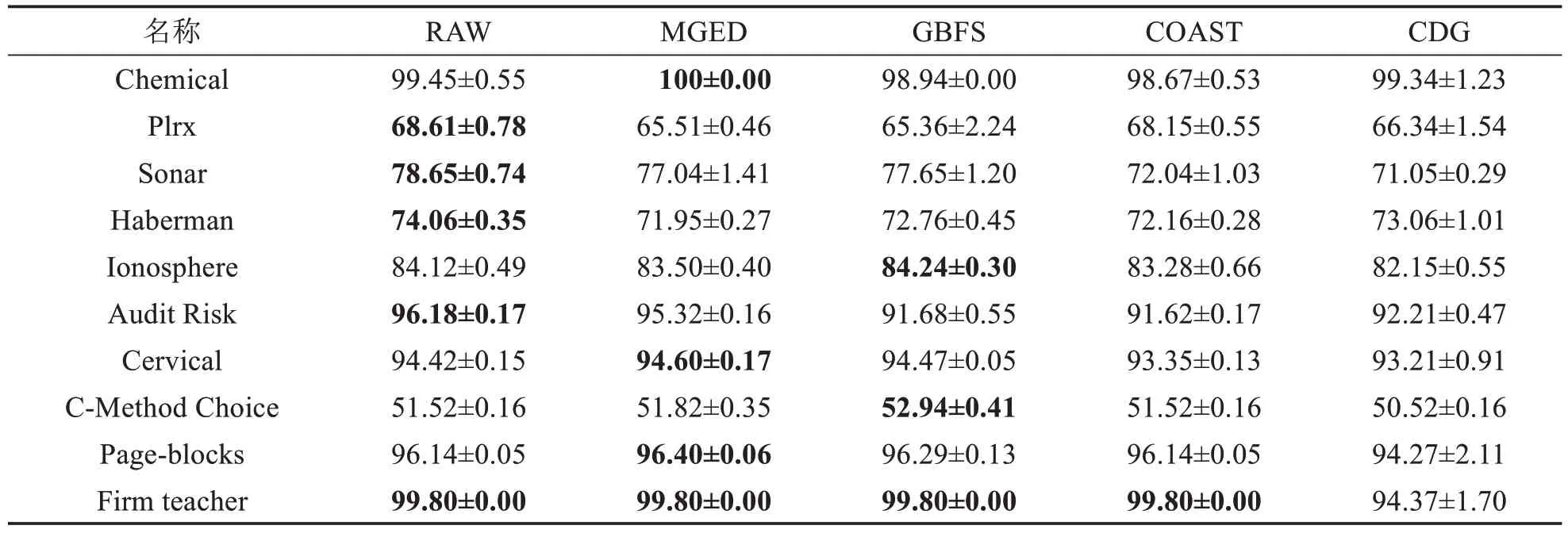
表9 KNN分类器(k=2)上的精度比较Tab.9 Accuracy comparison on classifier (k=2) KNN (单位: %)
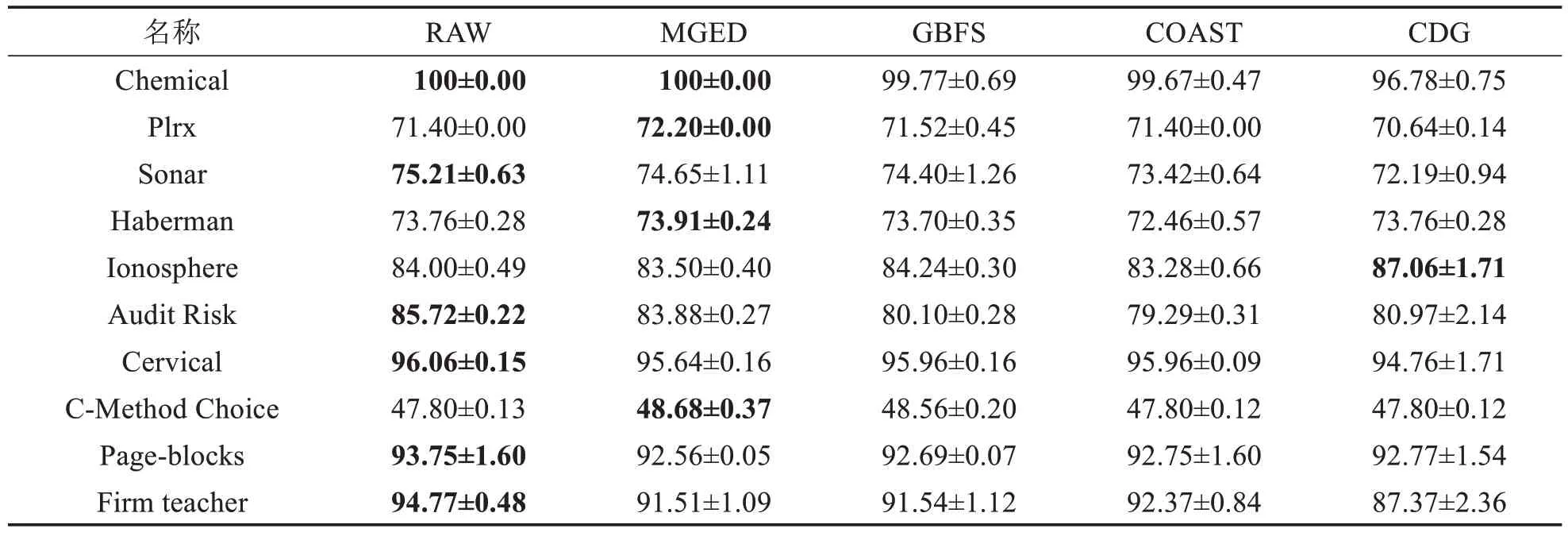
表10 SDA分类器上的精度比较Tab.10 Accuracy comparison on SDA classifier (单位: %)
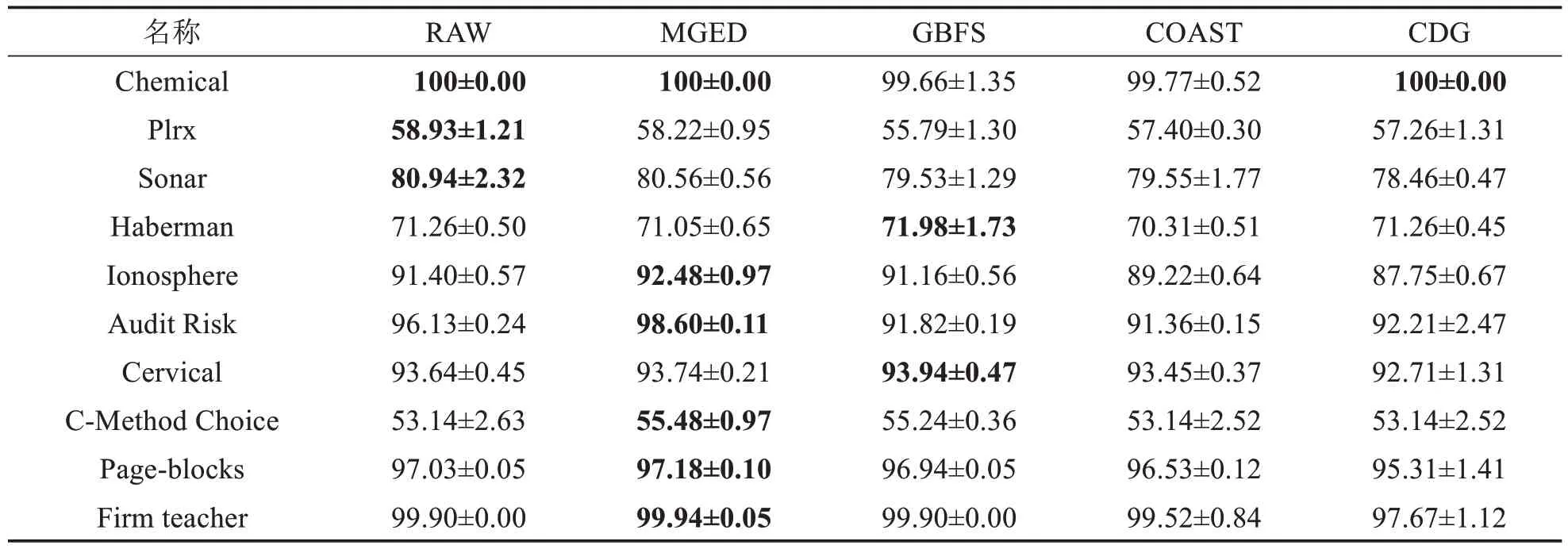
表11 3N分类器上的精度比较Tab.11 Accuracy comparison on classifier 3N (单位: %)
由表6~11可得,MGED算法的分类精度较于GBFS算法与最粗尺度,具有一定优势.对于Chemical数据集,仅有MGED 算法在各个分类器上将分类精度保持在100%.MGED 算法在CART、LDA、SVM 与3N分类器上都有较好的表现.在KNN 与SDA 分类器上,分类精度接近原始数据的分类精度,对于GBFS 算法与CDG算法,MGED算法对多尺度信息系统进行特征选择时能保持相对较好的分类训练精度.
为了探究MGED 算法、GBFS 算法与CED 算法是否具有统计学上的差异,对三个算法进行Friedman检验.首先,假设三个算法的性能相同,当α=0.05 时,qα=0.05=2.344,F(2,18)的临界值为3.555.在CART 分类器上的ΤF=2.650 5,在LDA 与3N 分类器上的ΤF值均为4.483 1,在SVM 分类器上的ΤF=4.793,在KNN分类器上的ΤF=3.720,同时在SDA分类器上的ΤF=1.714.
可知在α=0.05 时,原假设在LDA、SVM、KNN 与3N 分类器上被拒绝.为了进一步验证结论,对其进行Nemenyi 后续检验,CD 值为1.048.结果如图4 所示,可以看出三个算法在CART 与SDA 分类器上并没有显著性差异,而在LDA、SVM、KNN与3N分类器上都有显著性差异,这与假设性检验结果一致.
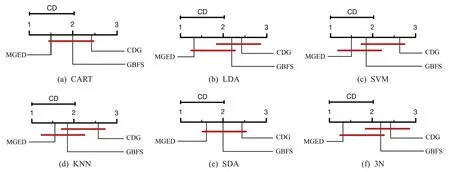
图4 分类学习精度的Nemenyi检验Fig.4 Nemenyi test for categorical learning accuracy
为了进一步验证MGED模型的有效性,对每个模型得到的特征子集在分类器上的训练时间进行对比,结果如图5所示.可以看出,MGED 算法在大部分数据集中,训练时间优于原始数据集及GBFS与CED 算法.在SVM分类器上,因为所有模型的训练时间较为接近,但是MGED算法在10个数据集中,有8个数据集的训练时间小于其他模型的训练时间.相较于最粗尺度,MGED算法在训练时间上依旧具有一定优势.
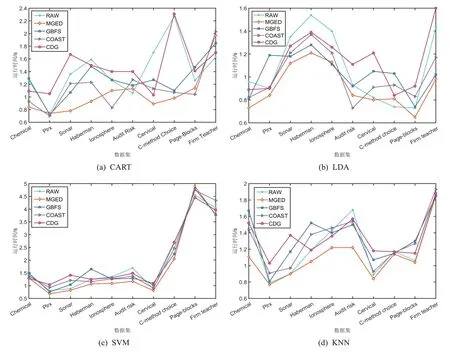
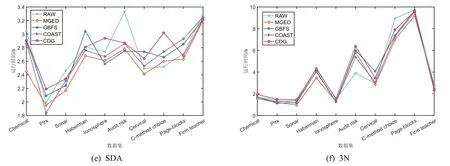
图5 模型在分类器上的训练时间对比Fig.5 Comparison of the training time of the model on the classifier
当尺度较粗时可能出现信息系统不协调的情况,故对分类训练时间有些许影响.在KNN分类器上的训练时间相较于其他模型具有较为明显的优势.整体上看MGED 算法能更好的去除冗余特征,更利于数据的分类与预测.
5 总结与展望
针对多尺度决策信息系统的最优尺度组合与特征选择问题,将图论思想与协调多尺度信息系统相结合,提出了基于超图的多尺度信息系统最优尺度特征求解算法.通过特征间的邻接关系构造多尺度决策信息系统诱导的邻接矩阵,利用超图将其可视化,将求解信息系统的特征选择子集与求解对应超图的极小顶点覆盖相联.从减少必要子集的数量入手,减少超图中不重要的超边数量,以此大幅减少特征选择的时间.因此,随着数据规模的增加,算法始终能保持相对较低的运行时间.数值实验结果表明,算法在分类训练精度上具有一定优势.在处理小数据集样本,运行稳定的同时大幅度减少陷入局部最优的情况发生.对于具有海量样本和高维特征的数据时,算法具有显著的时间优势以及相对较高的分类精度.今后将进一步研究如何优化极小相似对的生成算法,以及在多决策信息系统中的知识获取问题.

