考虑公平性的客舱乘务员排班研究

于 蓉, 郝蓉慧, 关欣怡

(1.中国民用航空飞行学院 空乘学院, 四川 广汉618307; 2.中国民用航空飞行学院 机场学院, 四川 广汉 618307; 3.中国民用航空飞行学院 经济与管理学院, 四川 广汉618307)

随着中国的经济正在快速增长,旅客出行的选择也越来越多样化,这也使得航空运输企业之间的竞争越来越激烈。航司对于客舱乘务员群体的需求量也将与日俱增,但近年研究显示客舱乘务员流失比例逐年增加[1-3],其中资源配置管理中排班公平性占主要原因。

由于客舱乘务员排班不公平的现象日益凸显,导致客舱乘务员流失率持续攀升,这不仅给航空公司带来了巨大的经济负担和时间成本。排班不公平导致出现同一个客舱乘务员有连续飞行一个月早班的情况,在进行飞行任务时容易导致工作能力和工作效率下降的状况。不公平的同时也会导致飞行安全存在隐患,客舱乘务员的休息如果得不到保证,容易产生身体疲倦,在遇到紧急特殊情况时不能及时做出反应,造成致命的航空事故。客舱乘务员流失也会降低人员队伍的稳定性。因此,如何提高客舱乘务员排班公平性从而减少客舱乘务员流失、飞行安全隐患是航空公司尚待解决的重中之重。

国内外学者针对客舱乘务员排班的问题做了相关研究。Dusan和Panta[4]采用“逐日”的算法,将工作任务以最小时间单位天进行安排,按照自然月顺序依次分配工作任务,直到满足所有客舱乘务员的工作量最大值结束。Gamache等[5]采用“单人”算法,以客舱乘务员为单位,先给第一位客舱乘务员安排工作任务结束后,再给第二个客舱乘务员安排工作任务,以此类推直至所有的客舱乘务员工作任务安排结束。Panta和Dusan[6-7]采用贪心算法与模拟退火、遗传算法、禁忌搜索等多种启发式方法成功地解决了60名客舱乘务员以及近600个航班的排班问题。饶云波[8]提出了一种新的排班系统,通过FP-growth算法,可以有效地将混合排班的数据库中的冲突元素按照一定的顺序进行降序,从而实现有效的冲突解决。张应辉[9]首次利用模拟退火算法并深入研究了如何有效地安排乘务员的工作时间,同时对“一个乘务员接一个乘务员排班”方法进行了改进,提高了乘务员排班的效率和准确性。陈骏[10]利用GASA混合算法有效地解决了乘务员排班系统的复杂性,取得了显著的成果。沈中林[11]采用基于Paretoz最优的粒子群算法,考虑同等级乘务员的飞行时间差异最小和航程起降次数差异最小这两个目标对604个航班、326个乘务员进行仿真排班。陈侨[12]首次尝试通过启发式搜索和贪心算法来改善乘务员的排班,解决了人员飞行时间的均衡。Michel等[13]、Torsten等[14]、Meinolf等[15]结合线性规划中的对偶理论,采用列生成算法缩小了乘务员排班问题的求解规模。

综上所述,专家学者大多对乘务员排班的方法进行研究,但考虑客舱乘务员排班公平性的研究甚少。且在考虑客舱乘务员排班目标方面,多数都是以航司的角度考虑成本因素,同时对于飞行任务多以航班作为最小单位,使得排班问题复杂度较高。因此,基于已有的理论和文献,为客舱乘务员排班问题的复杂度,本文首先生成满足限制条件的任务环,将最小工作单位从航班转化成任务环。同时,在任务环的基础上,考虑飞行时间、过早过晚航班、客舱乘务员人数这三个要素建立公平性排班模型,采用遗传算法对实际数据进行验证,证明其可行性。

1 客舱乘务员排班分析

在航空运输生产过程中,由于考虑自然条件、生产要素、风俗习惯等各方面因素的影响,整个货运和客运的相关时长会出现一定规律的季节性波动,因此航班时刻表也由于季节的不同有很大的区别。航空公司为了能有效且准确地得出航班计划表,需提前半年进行航班计划表的排班工作,从而产生下一个季节相应的乘务员飞行计划表。不同季节的航线、机型还有航班班次都需要变更,这就需要航司对每个月的乘务员飞行计划在执行前根据不同的需求做一个适当的调整和改动,产生每个月的乘务员飞行计划表。乘务员排班具体流程如图1所示。

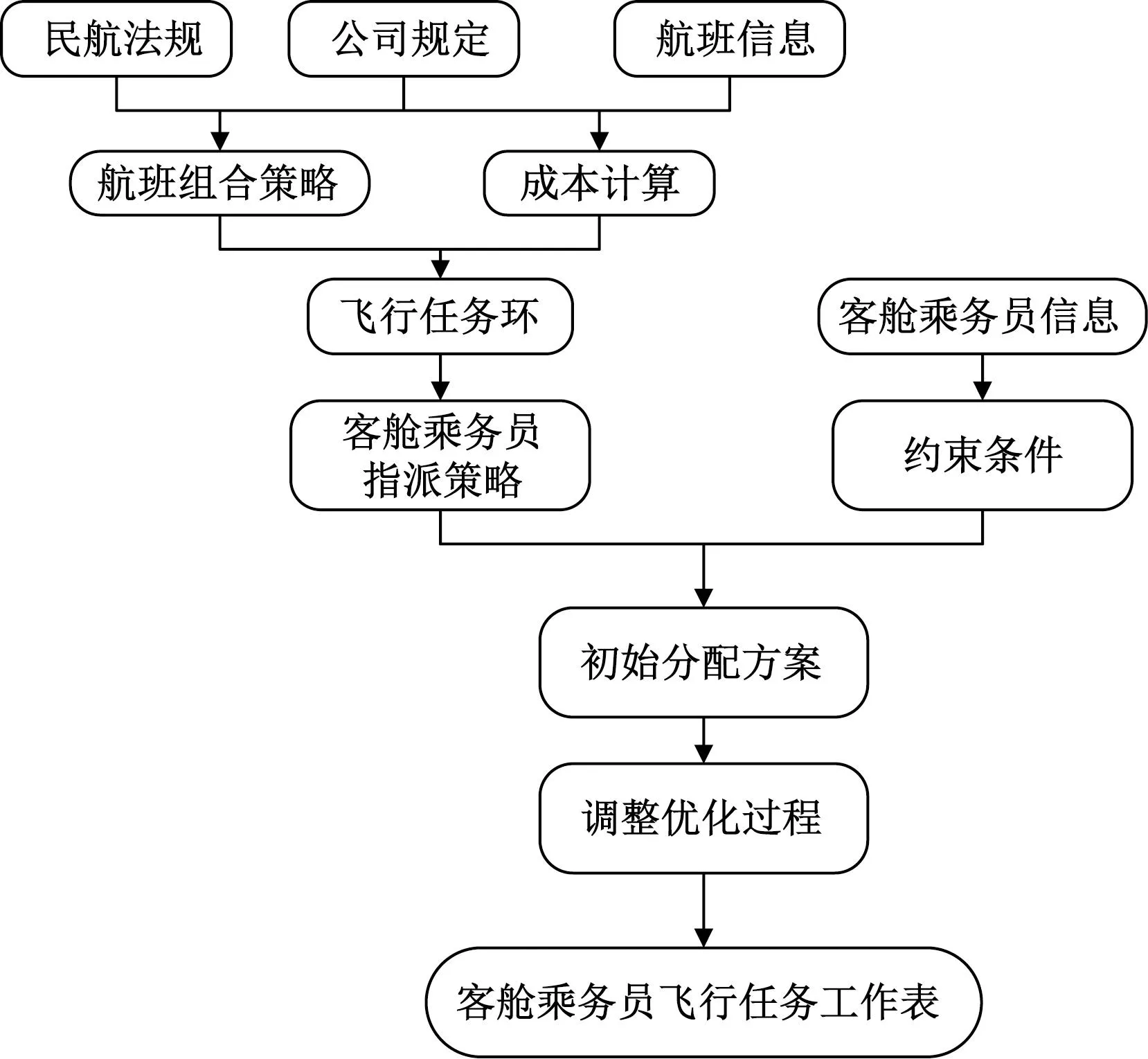
图1 客舱乘务员排班流程

2 航班任务环

2.1 任务环相关概念

在进行客舱乘务员排班之前,需要建立在任务环生成的条件下,所以第一步需要先生成符合规则的任务环,接下来阐述任务环的具体概念。

航班段(flight segment)是指飞机经过一次起飞、降落的飞行任务。它是客舱乘务员排班中的基本单位。如果航班中间没有经停,该情况只包含仅此一个航段;如果航班有经停,这说明该航班由多个航段组成。

任务(duty)是指两个及以上的航班满足空间时间限制所连接的有序序列,一般指一天内航班序列。其中限制条件包括航班在空间和时间上是连续的;两个连续的航班之间必须满足最大/小间隔时间;该任务的总飞行时间也有明确的限制时间。

任务环(pairing)是指由多个任务组成的接续序列,其中起始地与终点地必须是同一个乘务基地。任务环相关限制条件有任务环的第一个任务的出发机场必须是乘务基地,通常是指乘务员的住宅所在地,最后一个任务的到达机场也必须是乘务基地;任务环的最大任务数量,最长执勤时间、最大休息时间等。

2.2 任务环模型

任务环模型相关限制条件:每一个航班的到达机场与下一个航班起飞机场保持一致;在一个任务环中起发航班的机场与该任务环最后一个航班的到达机场保持一致;在一个任务环中任务相互不冲突;一个任务环的总执勤时间不超过12小时;每个任务环的机型保持一致;任务环的周期时长不能超过4天。

任务环模型为

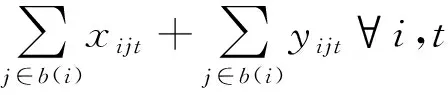
(1)

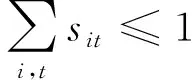
(2)

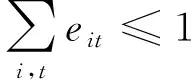
(3)

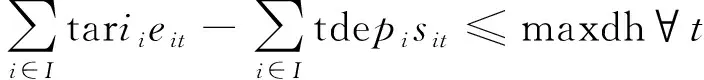
(4)

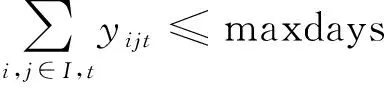
(5)

xijt,yijt,sit,eit∈{0,1}

(6)

式中:i为航班,i∈I,I为所有待执行航班集合;t为时间,t∈T,T为日期总和集合;h(i)为i航班的前导航班;b(i)为i航班的后序航班;sit为t日任务环是否从i航班开始的决策变量,sit为0～1的变量;eit为t日任务环是否从i航班结束的决策变量,eit为0～1的变量;xijt为t日i航班是否与j航班连接的决策变量,xijt为0～1的变量;yijt为t日i航班是否与t+1日j航班连接的决策变量,yijt为0～1的变量;tarii为i航班串的起飞时刻;tdepi为i航班串的降落时刻;max dh为机组每天的最大执勤时间;max days为任务环的最大天数跨度。式(1)为主要约束条件,包括地点衔接约束、时间衔接约束及流量平衡约束;式(2)为任务环只有一个起点;式(3)为任务环只有一个终点;式(4)为客舱乘务员每天的执勤时间不超过最大执勤时间,maxdh=12 h;执勤时间是转机、等待、飞行等所有总和的时间,等于降落时刻-起飞时刻;式(5)为任务环的时间跨度不超过规定的最长天数约束,max days=4 d;式(6)中xijt,yijt,sit,eit均为0～1的变量。

3 公平性排班模型

由于采用了遗传算法,需要有一个适应度函数(工作负荷值)来评估客舱乘务安排的工作负荷程度,其计算公式为

W=xFlight Time+yEarly Late Count+

zCrew Members Count

(7)

式中:W为工作负荷;x、y、z为权重,三者之和为1;Flight Time为每个客舱乘务员执行任务环的飞行时间;Early Late Count为每个客舱乘务员执行任务环中的过早/过晚航班次数;Crew Members Count为每个客舱乘务员执行任务环中的过早/过晚航班次数。

Flight Time=f1+f2+…+fi,i=num of pairing

(8)

式中:fi为第i个任务环的飞行时间;num of pairing为任务环的数目。

Early Late Count=xi1+xi2,i=num of pairing

(9)

式中:xi1为i任务环中过早航班次数;xi2为i任务环中过晚航班次数。

Crew Members Count=(N1+N2+…+Ni)/i,

i=num of pairing

(10)

式中:N为每个任务环所需的客舱乘务员人数。

计算工作负荷(work load)值的主要步骤如下。

1)判断长途航班和短途航班: 首先,通过将航班飞行时长(flight period)转换为时间间隔对象,然后与中位数飞行时长进行比较,判断航班是否是长途航班。经计算发现本文实验数据中位数飞行时长为5 h 3 min,超过中位数飞行时长定义为长途航班,小于中位数飞行时长定义为短途航班。

2)计算起飞时间和降落时间是否过早或过晚: 将实际起飞时间和实际降落时间转换为日期时间对象。其次,检查起飞时间是否在早上8点之前或降落时间是否在晚上8点之后。统计过早或过晚的次数。

3)选取每个任务环需要的客舱乘务员的人数:其中每个航班乘务员人数为航司给定的值。

4)计算工作负荷的值:使用给定的权重系数(0.4、0.4、0.2),将长途航班时间、过早或过晚的次数和乘务员人数结合起来计算工作负荷值。其中长途航班时间和过早或过晚次数会对工作负荷产生影响,客舱乘务员人数的影响较小。最终得到每个航班的工作负荷值。

work load=0.4Flight Time+0.4Early Late Count+

0.2Crew Members Count

(11)

约束条件为

Subject to:

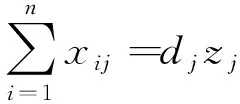
(12)

式中:xij为乘务员i是否指派到任务环j上,i=1,2,…,m;dj为第j个任务环所需的乘务员个数,j=1,2,…,n。

式(12)是指满足任务环的需要的人数。

xij≤zj

(13)

式中:zj=1时,第j个任务环被选中。式(13)满足乘务员i指派到任务环j要与选中任务环j数目保持一致。

xij+xih+cjh≤2

(14)

式中:xih为乘务员i是否指派到任务环h上;cjh=1:表示第j个任务环与第h个任务环在时间上重叠。

式(14)表示第i个乘务员在执行j、h任务环在时间上不重叠。

式(14)对于第i个乘务员在执行第j个任务环与第t个休息任务,这两者在时间上不重叠。

xij+yit+Rjt≤2

(15)

式中:yit=1时,表示第i个任务环执行第t个休息任务;RJt=1:表示第j个任务环与第t个休息任务冲突。

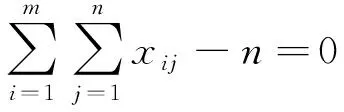
(16)

式(16)表示排班方案必须涵盖所有飞行任务环。

xij、zj、xih、cjh、yit、Rjt∈{0,1}

(17)

式中:xij、zj、xih、cjh、yit、Rjt为0～1的变量。

4 实例验证和分析

4.1 案例数据

采用我国某小型某航空公司一个月(9月)的航班计划进行乘务员排班规划,相关航班信息如表1所示。表1统计了航班数据的基本信息,包括航班号、基地、机型、日期、航程、实际起飞时间、实际降落时间、飞行时间及所需的客舱乘务员人数。根据表1数据,利用前文任务环模型生成564个可行任务环,运用公平性排班模型将564个可行任务环分配给航空公司的664名客舱乘务员。

表1 9月部分航班计划

4.2 模型算法

将航班数据进行收集整理后,采用遗传算法对乘务员排班模型进行求解。遗传算法是一种优化算法,通过模拟生物遗传过程中的选择、交叉和变异等操作来不断演化,以找到适应度最高(或最低)的解决方案。在这段代码中,遗传算法被用于寻找最优的工作调度方案,以最大限度地减少每个乘务员的总体工作量,并实现工作负荷的均衡分配。

具体步骤如下。

1)原始数据输入:任务环数目564个, 客舱乘务员人数664人。

2)定义参数: 定义遗传算法的相关参数,如种群大小、变异率、迭代次数等。

种群大小为100,变异率为0.1,迭代次数为100。

3)适应度函数: 定义适应度函数来评估每个染色体(工作调度)的优劣。利用适应度函数计算每个乘务员的总工作负荷,并将所有乘务员的工作负荷之和作为染色体的适应度值。

4)创建染色体: 创建一个染色体(工作调度)的方法。该方法随机将所有工作打乱,然后按照给定的乘务员数量分配工作,同一个乘务员第j个任务环与第t个休息任务时间上不重叠,直到所有的工作分配完毕。

5)变异操作:通过定义变异操作来引入随机性。在变异操作中,随机选择某个乘务员的工作,并随机交换该乘务员的某些工作,以增加染色体的多样性。

6)计算乘务员工作负荷: 计算每个乘务员的总工作负荷,以用于后续评估。

7)遗传算法主循环: 使用遗传算法的主循环,通过选择、交叉和变异等操作,生成新的染色体群体,并持续迭代一定次数,以逐步优化工作调度。

8)输出结果: 输出经过遗传算法优化后的最佳工作调度方案、最佳适应度值(总工作负荷)以及每个乘务员的工作负荷。

4.3 模型对比分析

为验证乘务员公平性排班模型的有效性,将航班计划数据分别采用考虑公平性的排班以及随机生成排班两种方式进行排班计算,通过对比乘务员工作负荷方差的方式来说明模型的有效性,方差越小说明,工作负荷越均衡,进而体现排班结果越公平。

工作负荷度方差的计算公式为

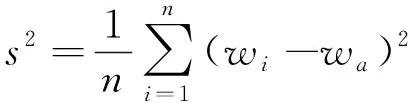
(18)

式中:s2为工作负荷度方差;i为第i个客舱乘务员,i=1,2,3,…,n;wi为第i个客舱乘务员的工作负荷度;wa为所有客舱乘务员的工作负荷度的平均值。

本文提出的优化方法基于生成可行任务环,采用工作负荷公式作为客舱乘务员公平性指标,使用python求解器运用遗传算法对公平性模型进行求解。表2展示了664名客舱乘务员的排班结果,其中包括乘务员执行的任务环序列集合、总飞行时间、过早过晚航班次数、工作负荷值。

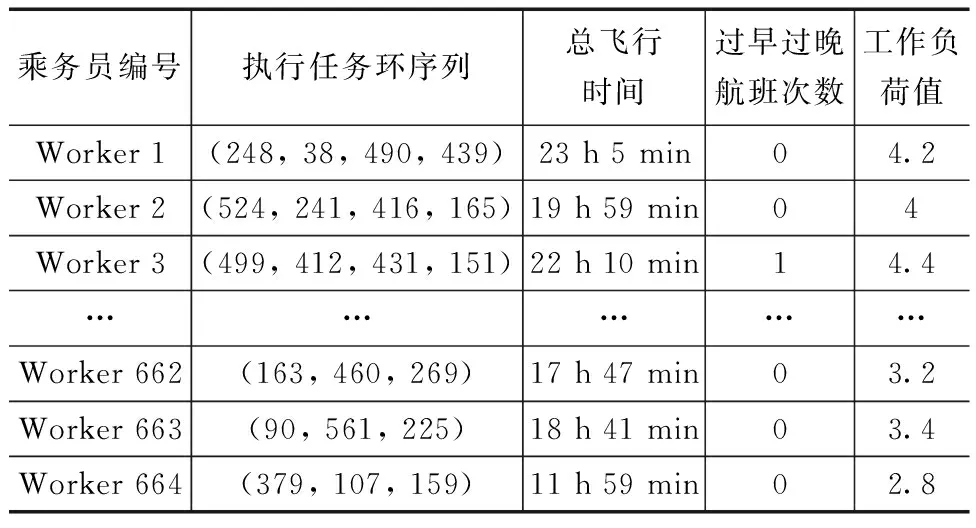
表2 客舱乘务员排班结果

表3展示了两种模型不同指标的对比结果,表3中的所有指标都围绕客舱乘务员的工作负荷值展开。

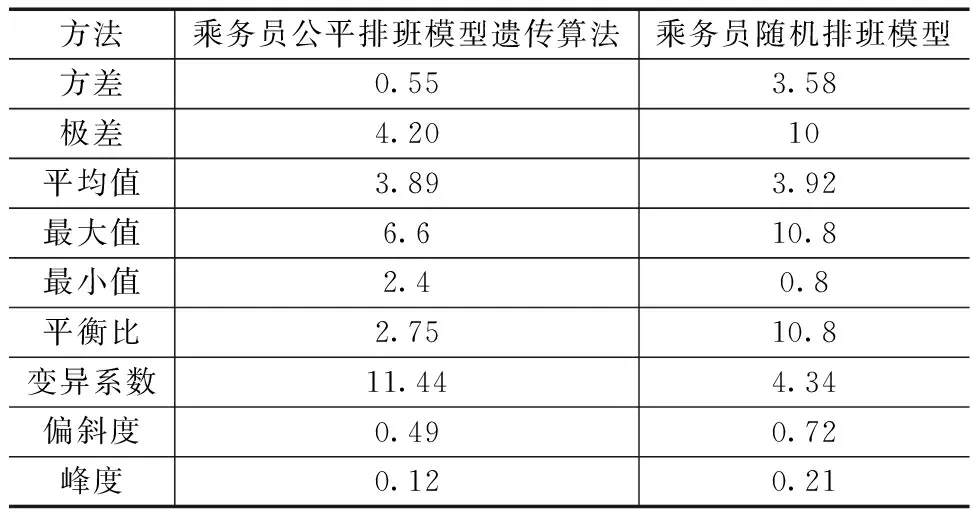
表3 模型对比结果

表3运用公平性模型的工作负荷方差为0.55,随机排班模型为3.58,方差越小说明排班结果更公平。极差的是工作负荷最大值与工作负荷最小值的差值,该值越小说明分配越公平,由表3可知,用公平性排班模型的极差为4.2,随机排班模型的工作范围为10,公平性排班模型更公平。工作负荷平衡比计算的是最大工作负荷与最小工作负荷的比值,用于衡量工作负荷在不同方法下的的平衡程度,该值越小说明工作量分配越均衡。由表3可知,用公平性排班模型的工作负荷均衡比为2.75,而随机派班模型的工作范围为10.8,公平性排班模型更公平。工作负荷度分布的偏斜度,即工作负荷度分布的不对称程度,接近零的偏度表示分配相对均衡,公平性排班模型(0.49)<随机排班模型(0.72),公平性排班模型更优。工作负荷度分布的峰度,即工作负荷度分布的尖锐程度,较小的峰度表示分配更均衡,公平性排班模型(0.12)<随机排班模型(0.21),公平性排班模型更优。

综上所述,针对客舱乘务员排班,用遗传算法求解的公平性排班模型结果比随机模型排班结果更优更公平,达到了实验初衷,具有一定的有效性。

5 结论

本文主要针对在满足限制约束条件形成任务环的基础上,考虑飞行时间、过早过晚次数、客舱乘务员人数三个方面制定乘务员公平排班模型,通过添加公平性约束条件,采用实际数据,运用遗传算法进行优化工作调度及排班结果。同时根据满足约束条件随机生成排班计划表,算出每个客舱乘务员的工作负荷值,对于两种方法下的方差结果进行对比,验证了该模型和算法的可行性和适用性。在刻画客舱乘务员公平性目标方面,只考虑了飞行时间、过早过晚次数、客舱乘务员人数,在实践过程中关注的还有过夜的天数、特殊航班的数量等多个公平性指标的均衡,实际问题中的考虑的优化目标众多,各个目标之间的参数大小协调十分困难,之后可以对这方面深入探讨和研究。