基于差分进化算法的二阶时滞系统参数辨识

李敏花,柏 猛

(山东科技大学电气信息系,山东 济南 250031)

0 引言

时滞现象广泛存在于各类生产过程中。由于时滞环节对系统控制性能有重要影响,时滞现象在过程控制领域受到广泛关注[1]。在实际应用中,通常将系统模型简化为一阶或二阶时滞系统模型,以便进行控制器设计[2]。获取时滞系统模型参数,特别是滞后时间参数,对控制系统的分析和设计具有重要意义[3]。目前,二阶时滞系统参数辨识方法主要包括时域法[4]和频域法[5]这2类。时域法通过对系统输入输出数据进行拟合,以实现参数估计。这类方法简单、有效,适用范围广,但辨识结果易受观测噪声影响。频域法对系统输入特定的、满足辨识要求的信号,根据系统频域特性获取系统参数。这类方法抗噪性强、算法复杂,对系统输入/输出数据要求高。系统阶跃响应辨识系统模型是1种简单、有效的时域辨识方法,广泛应用于控制领域。目前,由阶跃响应辨识系统传递函数的方法主要包括两点法、相良节夫法、半对数法和面积法等。这些方法可以在一定程度上解决二阶时滞系统的参数辨识问题。但总体而言,这些方法的辨识结果易受观测噪声影响,其参数估计精度有待提高。

对此,本文提出1种基于差分进化(differential evolution,DE)算法的二阶时滞系统参数辨识方法。该方法将系统参数估计问题转换为阶跃响应数据的拟合问题,通过采用DE算法进行优化,可有效提高参数估计的准确性和鲁棒性。

1 二阶时滞系统参数估计方法

1.1 问题提出

二阶时滞系统模型可表示为:

(1)

式中:a1和a2为模型参数;k为系统增益;τ为滞后时间。

根据系统阻尼比是否大于1,可将系统分为二阶过阻尼时滞系统和二阶欠阻尼时滞系统。

①二阶过阻尼时滞系统。

典型的二阶过阻尼时滞系统传递函数可表示为:

(2)

式中:T1和T2为时间常数。

式(2)与式(1)有参数关系,即a1=T1+T2、a2=T1T2。

零初始状态下,二阶过阻尼时滞系统单位阶跃响应可表示为:

H(t-τ)

(3)

当T1=0或T2=0时,式(2)可转化为一阶时滞系统,即:

(4)

一阶时滞系统的单位阶跃响应可表示为:

(5)

②二阶欠阻尼时滞系统。

二阶欠阻尼时滞系统传递函数可表示为:

(6)

式中:ξ为阻尼比,0<ξ<1;wn为自然频率。

在零初始状态下,二阶欠阻尼时滞系统单位阶跃响应可表示为:

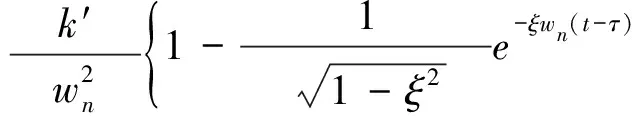
(7)

假设在ti时刻,二阶时滞系统阶跃响应y(ti)的观测值为z(ti),即:

z(ti)=y(ti)+v(ti)

(8)

式中:v(ti)为观测噪声,i=1,2,…,m,m为数据采集个数。

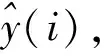
(9)

式中:J(θ)为目标函数。

本文取J(θ)为:

(10)

显然,目标函数J(θ)的极小化问题是典型的非线性最优化问题。经典求解方法,如Guass-Newton方法、Levenberg-Marquarat方法等,大多属于局部优化方法[6]。这类方法需给定合适的参数初值,否则无法收敛到全局最优解。为获得式(10)的全局最优解,本文采用DE算法对J(θ)进行优化。

1.2 DE算法

DE算法是由Storn和Price于1995年提出的1种智能进化算法。该算法采用实数编码,通过引入变异、交叉和选择这3种算子实现种群进化。研究结果表明,DE算法在求解非线性最优化问题时具有良好的全局收敛性[7]。同时,DE算法还具有算法简单、易于实现、可靠性和鲁棒性强的特点,非常适用于求解数值优化问题,因此被广泛应用于各类优化问题的求解[8]。

针对式(10)所示的J(θ)优化问题,为便于描述,本文令X=0。对于式(4)所示的一阶时滞系统,θ=[k,T,τ],即X=[x1,x2,x3]。对于式(2)所示的二阶过阻尼和欠阻尼系统,θ分别取θ1=[k,T1,T2,τ]和θ2=[k′,ξ,wn,τ],即X=[x1,x2,x3,x4]。采用DE算法估计未知参数θ的主要步骤如下。

①种群初始化。

本文假设X的维数为D(对于二阶时滞系统D=4),并且X取值的上限和下限分别为Xmax={x1,max,x2,max,…,xD,max}和Xmin={x1,min,x2,min,…,xD,min},则在Xmin和Xmax范围内,随机生成N个D维向量{X1,X2,…,XN}作为初始种群。对于任一向量Xi中的第j个元素xi,j,其生成方法如下。

xi,j=xj,min+rand[a,b]×(xj,max-xj,min)

(11)

式中:rand[a,b]为在区间[a,b]服从均匀分布的随机数。

式(11)取a=0、b=1。

在上述过程中,N为种群规模(数量),一般取N∈[5D,10D]。综合考虑算法效率和收敛性,本文取N=10D。

②变异操作。

对当前种群X1,X2,…,XN中的任一向量Xi产生相应的变异个体Vi:

Vi=Xr1+Fi(Xr2-Xr3)

(12)

式中:Xr1、Xr2和Xr3为在当前种群中随机选择的互不相同且与Xi不同的3个向量;Fi∈(0,1)为缩放因子。

③交叉操作。

将当前种群中的任一向量Xi与其变异个体Vi进行交叉,生成新的测试个体Ui。Ui中的第j个元素ui,j为:

(13)

式中:Ri,j=rand[0,1]为ui,j对应的随机数;Ci∈[0,1]为Ui对应的交叉概率。

④选择操作。

(14)

通过上述过程,生成新一代种群{X′1,X′2,…,X′N}继续进行迭代,直到满足迭代终止条件。

在DE算法中,缩放因子Fi和交叉概率Ci的设置对算法性能有重要影响,Fi和Ci的选择与目标函数特性紧密相关。由于不同二阶时滞系统所对应目标函数J(θ)的特性不同,为减小Fi和Ci对参数估计收敛性的影响,本文采用“either-or”策略[9]取代变异和交叉算子。采用“either-or”策略产生Ui的方法如下。

(15)

式中:pF∈[0,1]为变异概率;Ki为设定的参数,一般取Ki=0.5(Fi+1)。

研究结果表明[9],当Fi∈[0.5,1]、pF在大范围内取值时,DE算法均可取得较好的优化结果。基于此,为简化二阶时滞系统参数辨识方法的参数选择过程,本文取pF=0.5、Fi=rand[0.5,1]。

1.3 模型参数辨识方法

综上所述,本文提出的采用DE算法估计二阶时滞系统未知参数θ的主要步骤如下。

①判断系统类型,确定未知参数。根据系统阶跃响应是否有超调判断系统类型,将二阶过阻尼和欠阻尼系统未知参数分别设定为θ1=[k,T1,T2,τ]和θ2=[k′,ξ,wn,τ]。

②设定DE算法迭代次数最大值Gmax和较小的迭代终止参数ε>0,确定未知参数θ的取值范围θmin和θmax,将式(10)作为目标函数,以产生初始种群。

③通过式(15)所示“either-or”策略产生试验个体,并采用式(14)所示的选择操作生成新一代种群。

④取当前种群中使目标函数最小的向量θbest作为解向量,判断迭代终止条件:当J[θbest]小于ε或迭代次数G大于Gmax时,迭代终止。若不满足迭代终止条件,则返回步骤③继续迭代。

2 仿真结果与分析

为检验本文所提参数估计方法的性能,本文分别对二阶过阻尼时滞系统、二阶欠阻尼时滞系统和高阶时滞系统进行参数估计试验。试验采用式(10)所示的J(θ)作为目标函数。为便于比较,试验在采用目标函数J(θ)作为评价函数的同时采用归一化均方根误差(normalized root mean square error,NRMSE)进行比较。NRMSE的值f可表示为[10]:

(16)

显然,参数估计结果越接近真值,则f值越大。通过比较准则函数值的大小,即可检验参数估计算法的性能。

2.1 无观测噪声的情况

本节主要检验本文方法在无观测噪声情况下的参数估计性能。试验中,DE算法最大迭代次数取Gmax=200、种群规模为40、采样周期Ts=0.01 s。试验分别取基于继电器反馈(relay feedback,RF)的辨识方法[11]、频域辨识(frequency identification,FI)方法[12]和本文方法的参数估计结果进行比较。

①二阶过阻尼时滞系统。

试验采用的二阶过阻尼时滞系统传递函数为:

(17)

系统待估计参数分别为a2=10、a1=11、k=1、τ=2。试验采用本文方法进行参数估计时,以式(3)作为拟合模型,0≤t≤70s,参数向量取θ=[k,T1,T2,τ],且有a1=T1+T2、a2=T1T2,参数取值范围为θmin=[0,0,0,0]和θmax=[5,15,15,5]。采用不同方法得到的G1参数估计结果如表1所示。

表1 G1参数估计结果

由表1可知:本文方法在估计二阶过阻尼时滞系统参数时具有很高的估计精度;FI方法估计效果较好;RF方法估计效果较差。G1参数估计收敛特性如图1所示。

图1 G1参数估计收敛特性

由图1可知,采用本文方法进行参数估计时迭代次数少于50次即可达到最优值,收敛速度较快。由此可见,本文方法可有效解决二阶过阻尼时滞系统的参数估计问题,具有较高的估计精度。

②二阶欠阻尼时滞系统。

试验采用的二阶欠阻尼时滞系统的传递函数为:

(18)

为便于与其他算法估计结果进行比较,本文将式(18)写成以下形式:

(19)

系统未知参数分别为a2=1、a1=1.5、k=1、τ=0.5。试验采用本文算法进行参数估计时,系统待估计参数向量取θ=[k′,ξ,wn,τ]。试验采用式(7)作为拟合模型,0≤t≤10s,参数取值范围为θmin=[0,0,0,0]和θmax=[2,1,5,2]。采用不同方法得到的G2参数估计结果如表2所示。

表2 G2参数估计结果

由表2可知,3种参数估计方法都可有效估计二阶欠阻尼时滞系统的未知参数。相比较而言,本文方法的参数估计精度优于其他2种方法。G2参数估计收敛特性如图2所示。

图2 G2参数估计收敛特性

由图2可知,本文方法具有较快的收敛速度,迭代次数少于50次即可达到最优值。由此可见,本文方法可有效解决二阶欠阻尼时滞系统的参数估计问题。

③高阶系统近似模型参数估计。

在实际应用中,常将高阶系统近似为二阶系统以便设计控制器。高阶系统近似模型的参数估计是设计控制系统时需解决的首要问题。试验对以下高阶系统进行近似:

(20)

由试验系统阶跃响应可知,该系统为过阻尼系统。因此,试验采用式(2)所示二阶过阻尼时滞系统模型对上述系统进行近似。在本文方法进行参数估计时,本文采用式(3)作为拟合模型,0≤t≤10s,参数向量取θ=[k,T1,T2,τ],参数范围取θmin=[0,0,0,0]和θmax=[2,5,5,5]。采用不同方法得到的G3参数估计结果如表3所示。

表3 G3参数估计结果

由表3可知,针对试验高阶系统的近似问题:RF方法辨识得到的近似系统效果较差;FI方法可获得较好的近似效果;本文方法辨识得到的近似系统与实际系统输出差距最小。G3参数估计收敛特性如图3所示。

图3 G3参数估计收敛特性

由图3可知,本文方法具有较快的收敛性,迭代次数在50次内即可达到最优值。由此可见,本文方法可有效解决高阶系统的低阶近似问题。

2.2 含有观测噪声的情况

为检验本文方法在不同噪声条件下的参数估计性能,本节采用式(17)所示二阶过阻尼时滞系统进行参数估计试验。试验中,系统模型在每种噪声强度下均进行30次参数估计试验,取估计结果的均值和均方差作为参数估计结果。系统观测噪声取高斯白噪声,输出信号噪信比(noise-to-signal ratio,NSR)定义为:

(21)

式中:{y(ti)}和{v(ti)}分别为系统阶跃响应输出信号和观测噪声的均方差。

试验中,DE算法的种群规模为40、最大迭代次数为tmax=400、采样周期Ts=0.01 s,其他参数关系及设置均与无噪声试验时相同。不同观测噪声情况下的参数估计结果如表4所示。

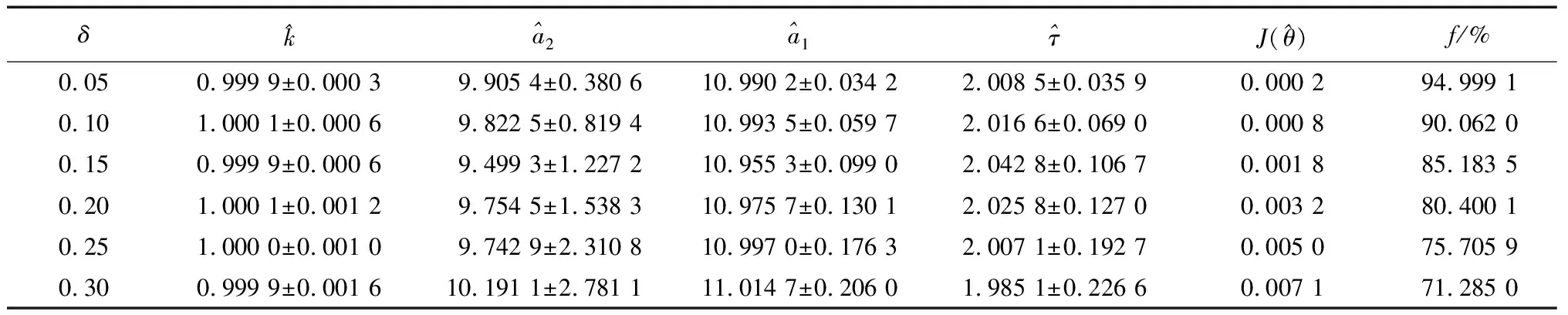
表4 不同观测噪声情况下的参数估计结果

由表4可知,当系统阶跃响应含有观察噪声时,本文方法依然可以获得较好的参数估计结果。其中,参数估计评价指标f值与NSR近似成线性关系,即f≈100-10×R。同时,由试验结果可以看出,当NSR较小(δ<0.2)时,参数辨识精度较高,方差较小;而当NSR较大(δ>0.2)时,参数估计结果误差较大。由此可知,当系统阶跃响应数据无观测噪声或噪声较小时,采用本文方法可获得满意的辨识结果;而当观察噪声较大时,参数辨识结果虽有一定偏差,但依然可为控制系统设计提供模型参考。

3 结论

本文提出的基于DE算法的二阶时滞系统参数辨识方法是1种根据系统阶跃响应估计系统未知参数的时域辨识方法。试验结果表明,该方法将参数估计问题转换为系统阶跃响应数据拟合问题,采用DE算法可有效解决二阶时滞系统的参数估计问题。与其他方法相比,本文方法只需根据系统阶跃响应即可辨识二阶系统未知参数,对系统输入输出数据要求较低,具有算法简单、可靠性高、适用性强和参数估计精度高的特点,非常适合工业应用。后续工作将主要研究多变量时滞系统的参数辨识问题和强观测噪声条件下低阶时滞系统的参数辨识问题。