声振信号分离提纯的风力发电机故障诊断方法研究

陈皓阳

(国华(江苏)风电有限公司,江苏 盐城 224200)

0 引言

风力发电需要在有风的环境下进行作业。由于风的方向与速度是随机的,致使发电机组长时间处于变负荷的工作状态。风量大的地方多处于郊区或者荒无人烟的区域。较为恶劣的环境会大幅增加发电机发生故障的风险[1-2]。发电机在正常运行状态下没有工作人员看守,导致工作人员在故障出现时不能及时处理并进行维修。这大幅降低了风力发电机组的使用寿命,增加了运营成本。

黄宏臣等[3]通过加速度包络解调方法对大型异步风力发电机滚动轴承早期故障诊断开展研究。该研究分别在单轴承故障诊断试验台和某型号大型异步风力发电机中,对轴承内圈滚道面上存在早期微弱损伤的滚动轴承进行试验,并验证加速度包络解调方法的有效性。王宏伟等[4]根据自适应灰狼优化的变分模态分解(adaptive grey wolf optimization-variational mode decomposition,AGWO-VMD)方法分解角域信号;通过规范化复合多尺度散布熵(normalized composite multiscale dispersion entropy,NCMDE)方式获取分解后与原始故障信号的特征,并组成特征向量;利用长短期记忆(long short-term memory,LSTM)模型完成特征向量的在线故障识别与诊断。但上述方法在风力发电机故障诊断过程中没有对受到噪声干扰的信号进行预处理,阻碍了对故障信息的正确分析与获取,进而给故障的准确诊断造成困难。

本文提出一种基于声振信号分离提纯的风力发电机在线故障诊断方法。该方法利用经验模态分解与小波阈值算法去除故障监测时的声音干扰信号,提高故障监测结果的精度;通过粒子群优化算法,解决在线故障诊断时间长与收敛速度慢的问题。

1 风力发电机故障分析和信号处理

1.1 风力发电机故障分析

导致风力发电机组出现故障的因素诸多,具体如下。

①齿轮箱。齿轮箱位于机舱内部,主要负责能量的传递,是风力发电机的主要设备之一[5]。齿轮箱内部结构较为复杂,由诸多变速齿轮与轴承组成。在风力发电机运作时,风速与负荷的突变会使得各齿轮间出现较大空隙,进而出现故障。

②发电机。发电机将齿轮箱传递的能量经过内部电磁感应转化成电能并传送出来。由于其工作时处于有风状态,较小的风沙颗粒极易进入内部,致使故障发生。同时,其内部的电磁环境也较为复杂,容易发生故障。

③叶片。叶片主要负责将流经叶片上的风能转化成机械能。由于风电场所处位置各不相同,叶片经常受酸雨、温度骤变等自然现象的影响,从安装起就经常处于空中旋转状态。长时间的不间断工作致使叶片材料的活性下降从而产生纹裂等,影响整个机组的使用寿命。

④螺旋桨。螺旋桨能够调节叶片旋转速度,分担齿轮箱与发电机等承担的大部分压力。但螺旋桨对阵风的敏感性较差。当系统转速变慢或者运行离散时,其不能很好地发挥自身作用。

综上所述,所有的电机故障均能通过振动信号被传感器采集到。

1.2 声音-振动信号分解

受大气紊流诱导风机振动、环境噪声、人为噪声等干扰源的干扰,风力发电机振动信号中参杂大量声音信号[6]。受到噪声干扰的振动信号具有非平稳、非线性的特点,给准确诊断风力发电机故障造成困难。为此,在故障信号中,本文利用振动信号参杂声音信号的波形图证明上述观点。

声振混合信号的特征分析如图1所示。

图1 声振混合信号的特征分析

由图1可知,声振信号处于高低频率叠加的状态,因而声音和振动信号分别处于高频和低频的位置。为了解决上述问题,本文设计了1种经验模态,将初始风力发电机在线故障信号分解成高频与低频这2个部分,即多个本征模态函数与1个残余量。计算过程为:

(1)

式中:ai(t)为初始故障信号,dB;bi(t)为ai(t)的模态函数;cn(t)为ai(t)的残余量;t为时刻,s。

在信号分解过程中会出现模态混叠现象。为此,本文采用噪声辅助信号处理方式对其进行完善。完善过程可称为集成经验模态。本文将初始故障信号引入高斯白噪声,使混叠的信号分解成不同尺度的分量,并将每个分量进行平均计算,从而获得最终的分解量。

集成经验模态根据白噪声信号频谱均匀分布的特性,使各频带信号反射至其对应的尺度。详细过程如下。

②对归一化处理后的信号经验模态进行分解,获得j个尺度分量ej(t)与1个残余量cn(t)(低频部分)。

③添加不同类型的白噪声信号,反复进行步骤①与步骤②,得出:

(2)

式中:a′i(t)为处理后的信号,dB。

④计算得出各分量总体均值,并去除高斯白噪声的干扰,获得集成经验模态最终的尺度分量e′j(t),即:

(3)

式中:n′为反复进行步骤③的次数。

1.3 小波阈值去噪

小波变换[7]的本质是针对信号时间与频率的分析,能够在时、频两方面凸显故障信号的局部特征。其在分析波动信号与获取信号的局部特征时具有极大的优势。

小波变换把各尺度分量的小波函数进行叠加。叠加过程即将基本小波函数进行σ位移后,在尺度β下与故障信号作内积运算,得出:

(4)

式中:W为傅里叶变换过程中使用参数的数值;β为尺度系数;x(t)为初始声音噪声信号,dB;σ为位移。

经济学是很多大学的热门专业，更有许多专业的财经类院校每年都会招生大量的经济管理专业学生，他们不仅需要掌握系统的经济学和管理学相关知识，包括财政学、金融学、经济学、统计学、管理学、审计学、税务学、会计学等内容非常丰富，还需要兼修文学、法学、理学、工学等多门知识，这样才能更好的满足就业需求，服务社会发展。我国已经进入经济发展新常态时期，现代经济管理对社会发展至关重要。

小波变换对应的频域Fx(β,σ)描述为:

(5)

式中:ω为尺度分量。

故障信号在时域上通常是连续的,而声音噪声信号的时域则是间断的。因此,经过小波变换后,得出小波系数模值较大。声音噪声具有极强的随机特性。通过高斯分布理论,可以控制噪声系数始终保持在(-3～+3)Sigma范围内。据此,只需去除区间内的系数,就能控制高斯白噪声。

通过对比故障信号失真情况与抑制高斯白噪声效果,本文选取小波分析层数为3,进而获得3个不同的小波系数值。

本文选用小波阈值计算方法中的固定阈值估计算法完成阈值求解。该方法能够去除模值极小的信号、节省计算时间,并有效去除噪声,与实际阈值结果基本相同。该方法去噪有2种函数形式,即硬阈值函数与软阈值函数。

硬阈值函数即当阈值大于小波系数时,设系数为0,则:

(6)

式中:T为阈值;Wn为阈值经过处理后的小波系数值。

当小波系数的绝对值小于阈值且等于0时,即可得到软阈值函数:

(7)

1.4 小波信号重构

小波信号重构即对各层系数按照特定的规则进行处理,并将去噪后的每一层小波系数进行合并,进而得出去噪后的振动故障信号。详细过程如下。

①采用集成经验模态分解含噪声的故障信号,获得j个振动模态ej(t)。

②对分量的高频与低频进行分离。

③将分量的高频部分按照小波阈值去噪方式进行重构,获得未含有声音噪声的分量。

④将分量的低频部分与步骤③得出的分量进行重构,得出实际风力发电机在线故障信号。

风力发电故障信号去噪流程如图2所示。

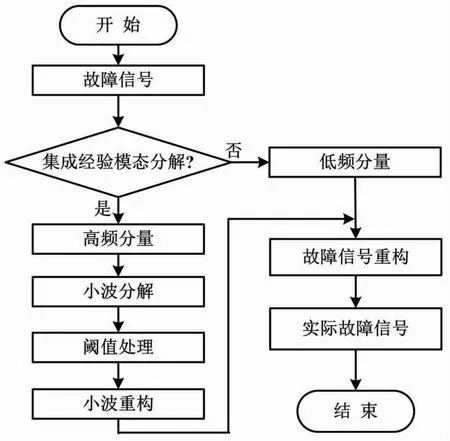
图2 风力发电故障信号去噪流程图

2 风力发电机在线故障诊断

反向传播(back propagation,BP)神经网络[8-9]的训练方式通常为误差逆向传播,在训练过程中可以得出某层的前馈网络。为了实时诊断故障,本文将最速下降算法作为学习规则,经过不断学习更新权值、阈值等参数,进而降低整个网络的误差。本文选用的3层BP神经网络结构中,各层间使用全互联手段,且相同层次间不能进行链接。BP神经网络结构如图3所示。

图3 BP神经网络结构示意图

由图3可知,诊断方法的全局搜索最优能力较差,且学习速率也未达到理想结果。为此,本文引入粒子群优化算法,完成风力发动机在线故障诊断。该算法可通过更新速度与位置,尽可能地得到全局最优解,并保证诊断结果的精准度。

(8)

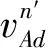
(9)

粒子群优化下的BP神经网络在线故障诊断[11-12],本质上就是先通过粒子群优化该网络的权值与偏置,再进行BP神经网络的训练,以获得风力发电机的在线故障诊断结果。详细过程如下。

①建立BP神经网络,设定网络相关参数、权值与偏置。

②将去除噪声后的风力发电机振动信号输入BP神经网络中,计算粒子群迭代过程中相关参数,即粒子的m、K、γ1与γ2等。

③求解各粒子的速度与位置。

④运算个体的适应度值,并与历史数值作对比。假设该值更优,则替换历史数值,进而更新当前位置。

⑤若粒子的全局最优解没有历史最优解好,则选用历史最优解作为全局最优解。

⑥各粒子根据式(8)、式(9)更新其速度与位置。

⑦判断更新后的速度与位置是否满足设定的范围。若不满足,就需要将边界值当做粒子的速度与位置。

⑧判断迭代计算次数是否符合设定的极限次数。若满足,终止迭代,输出权值与偏置;反之,则返回步骤④。

⑨根据步骤⑧得出的权值与偏置进行BP神经网络的训练,从而诊断出风力发电机的在线故障。

3 试验数据分析与研究

3.1 试验环境与参数设定

为了验证本文提出的基于声振信号分离提纯的风力发电机在线故障诊断方法在实际应用中的有效性,本文选用某电场1.5 MW风电机组作为试验对象。

1.5 MW风电机组的参数设置如下:额定功率为1.5 MW;风轮直径为5.8 m;输出电压为360 V;额定风速为12 m/s;频率为50 Hz;转速为1 500 rad/min;额定电流为900 A。

试验通过样本故障数据类型的数量与特征,设置输入层、隐含层与输出层的节点数量分别为5、12、4。在隐含层与输出层中,试验将Sigmoid型函数作为传递函数,以Trainlm型函数为训练函数。其训练次数设定为500,学习效率与误差分别为0.2与0.002。样本数据选取叶片侵蚀、气隙偏心、轴承润滑不良等故障数据,在机组上安装1个振动传感器,收集正常状态与各种故障类型的振动信号,并选取不同小波系数进行压缩。

3.2 风力发电机振动信号处理效果分析

整数-整数累积分布函数(cumulative distribution function,CDF)(2,2)与CDF(2,4)的压缩比与信噪比对比结果如图4所示。

图4 整数-整数CDF(2,2)与CDF(2,4)的压缩比与信噪比对比结果

由于风力发电机振动信号受外界大气紊流诱导、环境和人为等条件干扰而存在噪声,故采用本文提出的小波阈值算法去除信号噪声。风力发电机振动信号去噪效果如图5所示。

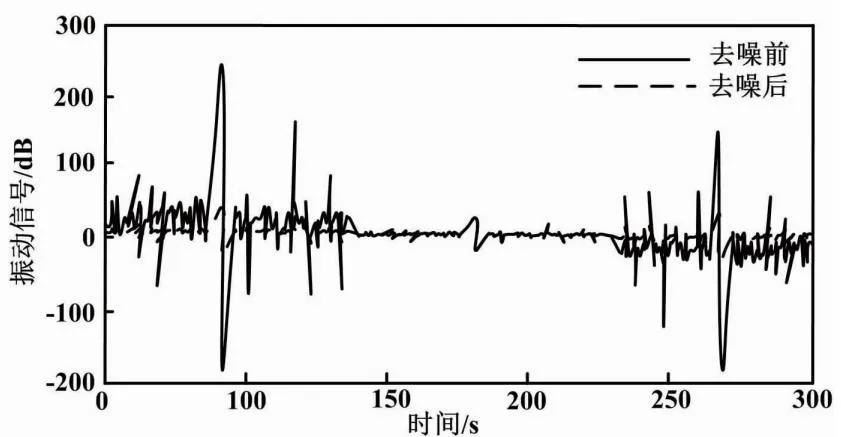
图5 风力发电机振动信号去噪效果

由图5可知,大气紊流诱导风机振动、环境噪声干扰、人为噪声干扰等典型干扰源不会对后续的风力发电机在线故障诊断造成影响。这是因为本文采用小波阈值算法能够有效去除风力发电机振动信号中的噪声,使后续的故障诊断精度得到提升。

本文将去噪后的风力发电机振动信号分量与低频分量作重构处理,得到风力发电机的实际故障振动信号。经过本文方法处理后的振动信号情况如图6所示。

图6 经过本文方法处理后的振动信号情况

风力发电机的振动信号经过本文方法处理后,特征得到凸显。未经过处理的正常信号与故障信号差距并不明显,且不同故障难以区分。本文去除了声音噪声,使正常信号与故障信号间的差距明显,且不同故障间差距也极为显著,易于后续BP神经网络的故障诊断。

3.3 故障诊断精度对比

试验采用本文方法、文献[3]方法与文献[4]方法,对风力发电机在线故障诊断精度进行对比。风力发电机在线故障诊断精度对比结果如图7所示。

图7 风力发电机在线故障诊断精度对比结果

由图7可知,本文方法进行风力发电机在线故障诊断的精度最高可达100%。其故障诊断精度始终高于文献[3]方法和文献[4]方法。这是因为本文方法利用集成经验模态将故障信号的高频与低频分离,通过小波阈值过滤噪声部分并与低频部分重构,得出不含有噪声的故障数据,进而有效提升故障数据的诊断精度。

3.4 故障诊断时长对比

试验采用本文方法、文献[3]方法与文献[4]方法,对风力发电机在线故障诊断时长进行对比。风力发电机在线故障诊断时长对比结果如图8所示。

图8 风力发电机在线故障诊断时长对比结果

由图8可知,本文方法采用粒子群优化算法,能够不断更新速度与位置,得到全局最优解、提升学习速率,并快速、精准地诊断出风力发电机故障。本文方法在第22次训练时达到收敛,且误差极小。文献[3]方法极易陷入局部最优的问题,且风力发电机在线故障诊断能力较差,在第47次训练时才达到收敛。文献[4]方法结构复杂,在第56次训练时达到收敛。该方法处理数据能力存在不足,得出的均方误差远大于本文方法。由此可证实本文方法的训练次数较少,风力发电机在线故障诊断时间较短,并且风力发电机在线故障诊断性能较好。

4 结论

由于风力发电在线故障诊断误差较大,同时还会增加成本,故本文采用分频方法完成其在线故障诊断。本文根据集成经验模态、小波阈值算法得出不含有噪声的故障信号,通过粒子群优化算法、权重矩阵监测出该信号所在位置,并诊断出故障类型。试验验证本文方法在线故障识别能力优于文献[3]方法与文献[4]方法,并能够精准判断出故障类型,且训练收敛速度快。上述结果证明了本文方法的有效性。本文方法能够为日后深入研究风力发电机故障诊断提供理论依据。