基于KPCA-KNN算法的边坡稳定性预测*

王团辉,王 超,2,李岳峰,徐健珲,王琦玮

(1.昆明理工大学 国土资源工程学院,云南 昆明650093;2.自然资源部高原山地地质灾害预报预警与生态保护修复重点实验室,云南 昆明650093)

0 引言

近年来,随着社会经济的不断发展,岩土体工程数量快速增加,其中边坡安全问题受到了越来越多的关注。边坡失稳可能会对人民生命财产安全造成重大影响[1-3],自然资源部2022年发布的2021年全国地质灾害灾情统计数据显示,我国发生的滑坡事故数量为2 335起,占地质灾害总起数的48.93%,居于首位[4]。据2023年2月24日央视新闻报道,内蒙古自治区阿拉善盟阿拉善左旗新井煤业有限公司矿区发生山体滑坡,造成6人死亡,47人失联[5-6]。因此,边坡失稳防治是岩土工程的重要研究课题之一[7-8]。为了降低边坡失稳带来的危害,开展边坡稳定性预测研究十分必要[9]。

目前,边坡稳定性预测通常分为定量和定性两类方法。定性分析方法主要有地质分析法、工程地质类比法等[10-11],该类方法综合考虑了影响边坡的多种因素,但主观性较强。定量分析方法包括确定性分析和不确定性分析,确定性分析主要采用极限平衡法和数值分析法[12-13]。边坡工程是一个复杂的非线性系统[14],其稳定性受多种不确定性因素的影响。不确定性方法在处理非线性问题上具有较好的预测效果,随着人工智能算法的兴起,不确定性分析已成为目前常用的分析方法,如模糊层次综合评判法[15]、灰色关联度分析[16]、支持向量机(SVM)[17]、BP神经网络[18]、K近邻(KNN)[19]、随机森林(RF)[20]等。鉴于边坡岩土体的结构、岩土体构成及物理力学性质的不确定性和非线性特点[9],国内外学者多从降维的角度出发进行边坡稳定性研究,如:姚怡等[21]通过主成分分析(PCA)进行降维,消除指标之间的相关性,建立了径向核函数(ERBF)优化的SVM模型;EANG等[22]采用层次聚类分析(HCA)和主成分分析(PCA)对边坡稳定性进行了预测;IVANOV等[23]通过主成分分析对土质边坡稳定性的影响因素进行了特征提取;SANTOS 等[24]采用主成分分析、判别分析和置信度对露天矿边坡稳定性进行了评估;高峰等[25]利用PCA降低了数据的冗余性,建立了基于粒子群优化算法的极限学习机模型;冯泽杰[26]利用Z-Score主成分分析及代数迭代算法(ART)提高了边坡稳定性的预测精度;陈建宏等[27]建立了PCA和BP神经网络的预测模型,对边坡稳定性进行了预测;高文华等[28]利用PCA优化了BP神经网络的运行效率;宋鑫华等[29]建立了PCA-Logistic模型,其能够有效处理样本数据,提升模型的准确性。

以上研究都是基于PCA降维来消除指标之间的相关性,鲜有学者运用升维思想即用高维空间的线性运算来代替原始空间的非线性运算[30]。基于此,本文利用核主成分分析(KPCA)方法,通过维数提升来挖掘高维空间中特征之间的关联,使处理后的数据更易于分类,建立基于KPCA-KNN算法的边坡稳定性预测模型,旨在提高模型的分类性能和效率。

1 方法原理

1.1 核主成分分析

KPCA是一种基于核方法的非线性主成分分析方法,其核心原理见图1。核方法是一种基于核函数的学习算法,善于处理非线性问题,其核心思想是:将原始数据映射到更高维的空间进行线性运算,以减少计算量、提高运算效率。由于核主成分分析方法应用较广,在此不再赘述,详细计算步骤见文献[31]。

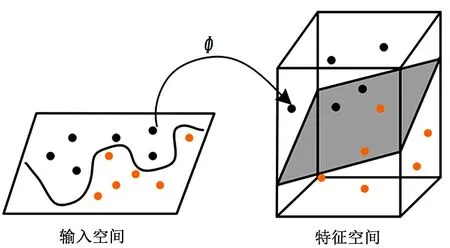
图1 KPCA核心原理[30]

1.2 K近邻算法

K近邻算法是一种常见的机器学习算法,能够高效处理分类和回归问题,其核心思想是:在确定各个样本之间距离的前提下,通过样本间的距离来界定该样本与特征空间内K个样本的亲疏关系,根据最相邻的K个样本的类别来判定该样本的所属类别[32],其核心原理见图2。

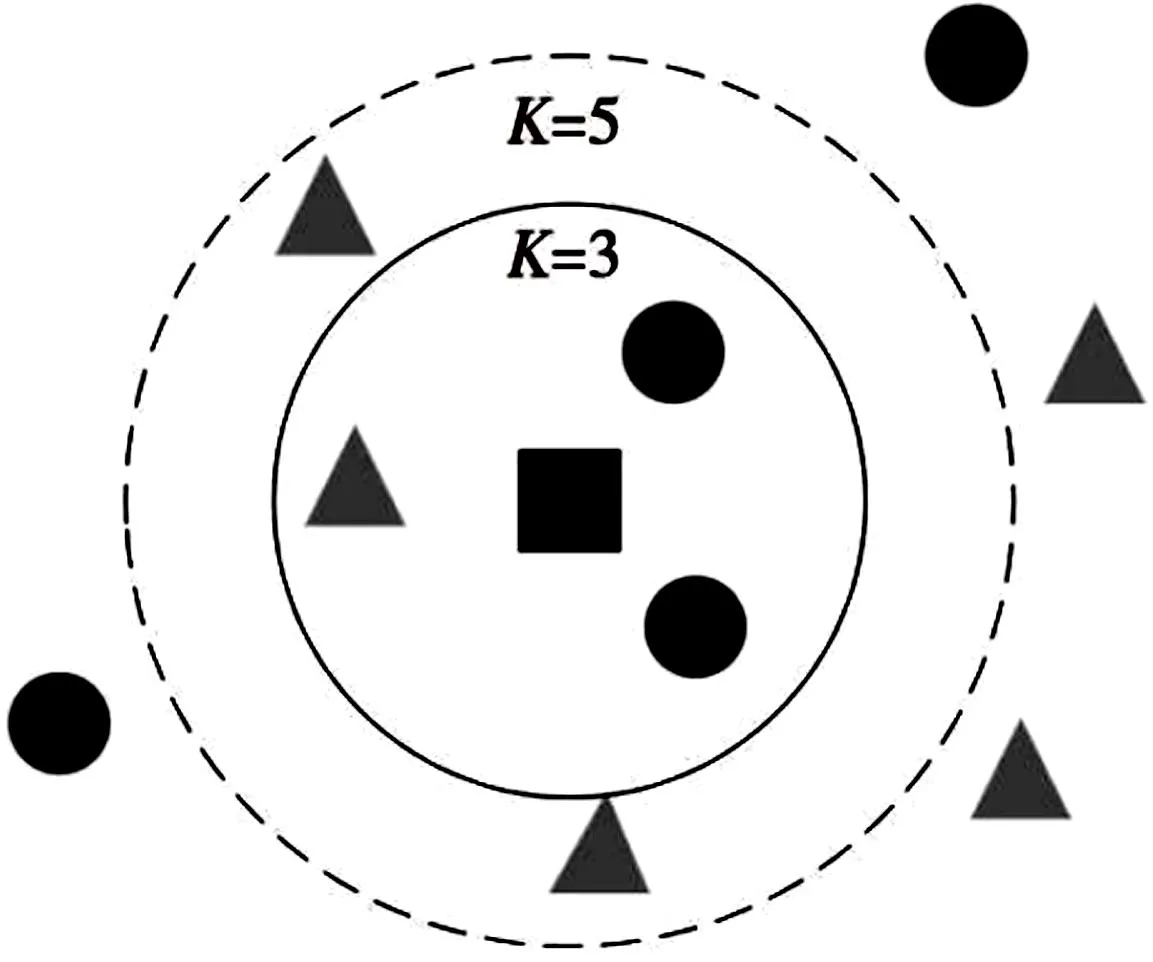
图2 K近邻算法核心原理[33]

若有n个训练对象,利用K近邻算法对待分类样本xnew进行分类。首先找到K个距离xnew最近的训练样本点,根据K组样本的类别投票确定xnew所属类别。距离可用欧氏距离计算:

(1)

式中,xi为已知类别样本。

2 KPCA-KNN边坡稳定性预测模型构建

2.1 指标选取及数据收集

在实际工程中,影响边坡稳定性的因素众多,主要包括地层、岩性、地质构造、地应力、岩体结构、水的作用、边坡的几何形状和表面形态等[34]。其中边坡高度、边坡角是基本的边坡几何参数;影响边坡稳定性的岩土体物理力学指标主要是容重、黏聚力、内摩擦角和孔隙压力比等。一般而言,岩土体的容重、黏聚力、内摩擦角越大,边坡越稳定;反之,则边坡越容易失稳[35]。在水的作用方面,可以用孔隙压力比来表征注液量变化和降雨过程[36]。借鉴前人的研究成果,选取容重(γ)、黏聚力(c)、内摩擦角(φ)、边坡角(φf)、边坡高度(H)、孔隙压力比(ru)等6个指标作为输入指标,边坡状态作为输出指标。模型构建流程见图3。本文在文献[37]所收集的边坡实例中选取55组样本建立数据库,部分数据见表1。

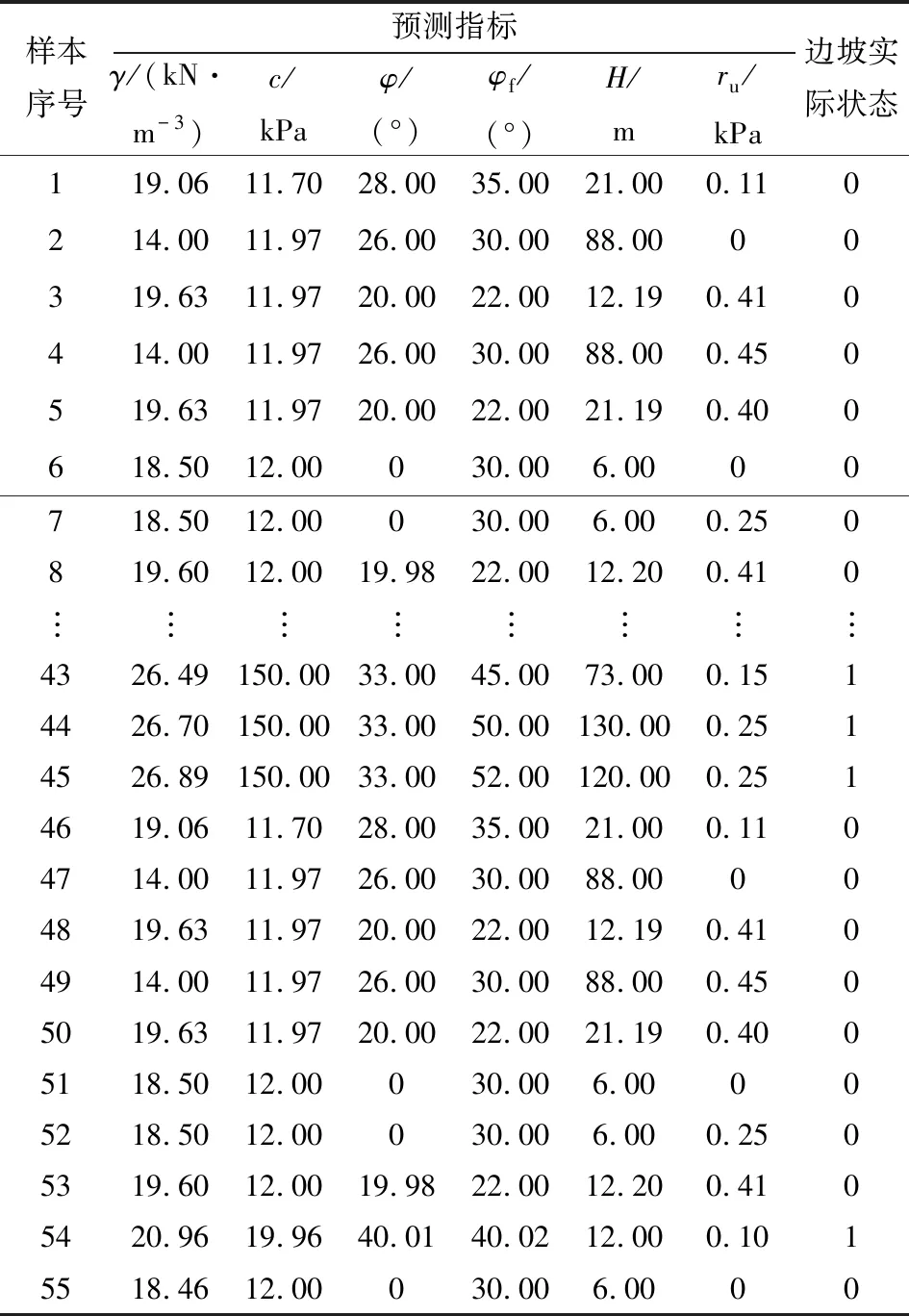
表1 样本原始数据

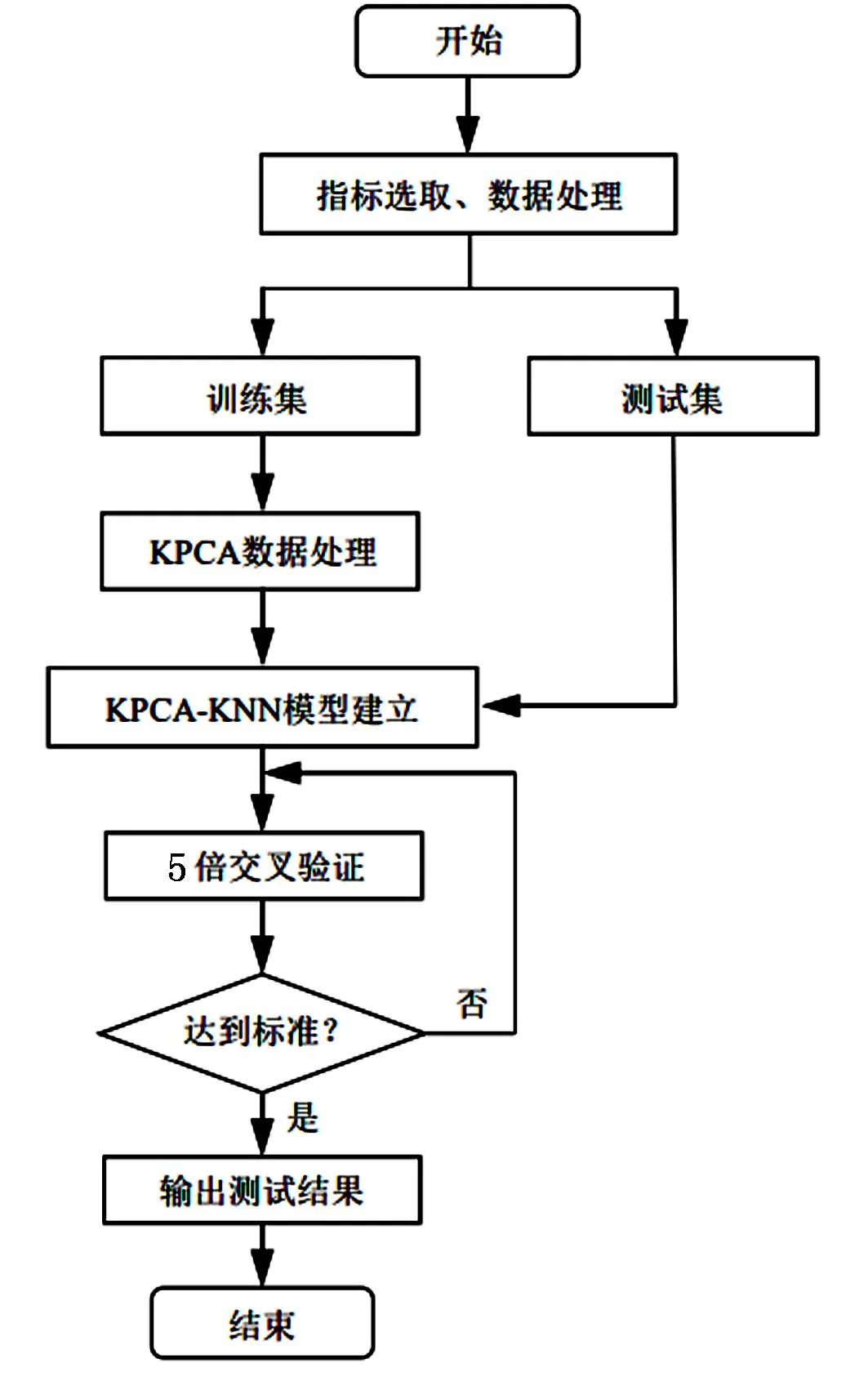
图3 模型构建流程

2.2 原始数据预处理

为了消除指标量纲对预测模型的影响,本文选取统一极差处理法对样本的原始数据进行处理[38],计算式为

(2)

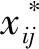
2.3 KPCA数据处理

将预处理后的样本数据进行KPCA处理,处理后的指标由K1-K6代替,得到的数据见表2。

表2 KPCA数据处理结果

2.4 KNN参数寻优

K值作为KNN算法的超参数之一,直接影响模型的性能。K值过小,训练误差减小,但会出现过拟合现象;K值过大,泛化能力提高,但误差增大,易出现欠拟合。本文结合文献[19]中的K值寻优方法,最后取最优K值为5。

2.5 KPCA-KNN模型预测结果

分别将KPCA处理前和处理后的数据划分为训练集(40个样本)和测试集(15个样本),将数据导入KNN模型并进行5倍交叉验证(交叉验证原理见图4)。

对测试集中的样本进行预测,结果见表3。由表3可知,本文模型的预测结果与实际等级完全吻合,而传统KNN模型、BP神经网络模型、SVM模型均出现了错判。

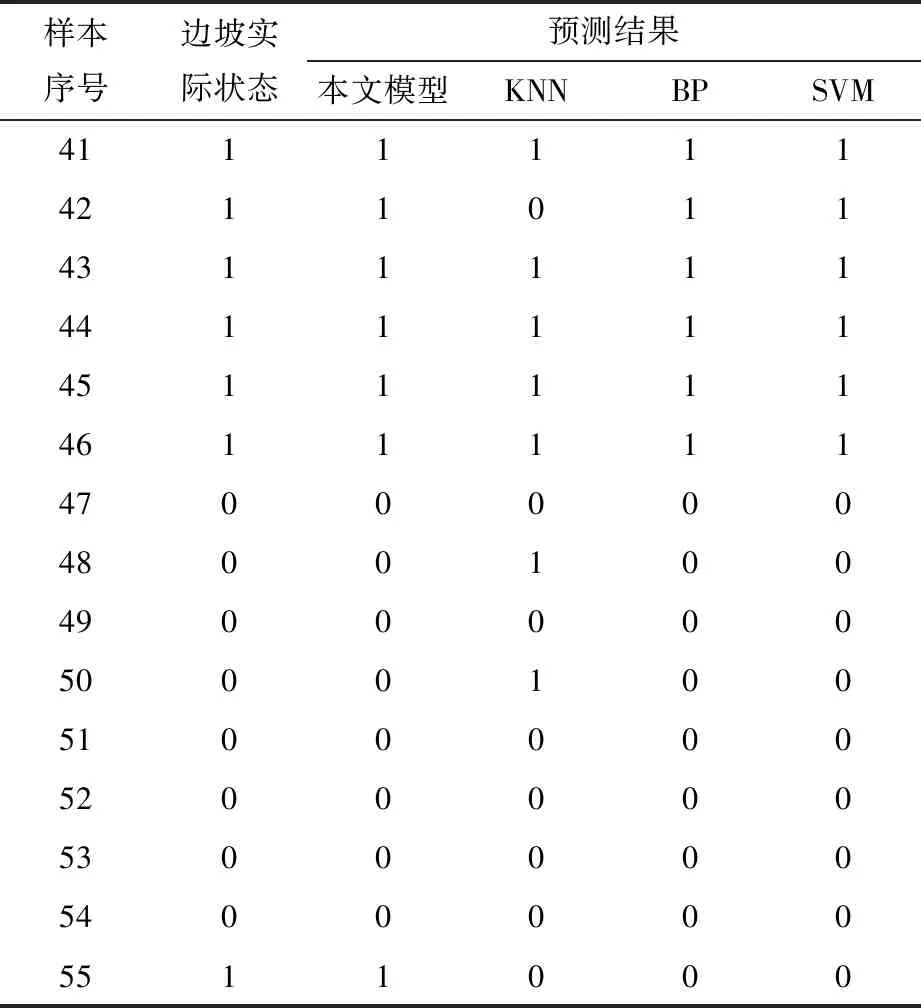
表3 测试集样本预测结果

各模型的准确率-召回率见图5。由图5可知,经过KPCA处理的KNN模型准确率和召回率均为100%,未经过KPCA处理的KNN模型则为70.6%,BP神经网络和SVM的准确率和召回率也不及本文模型。

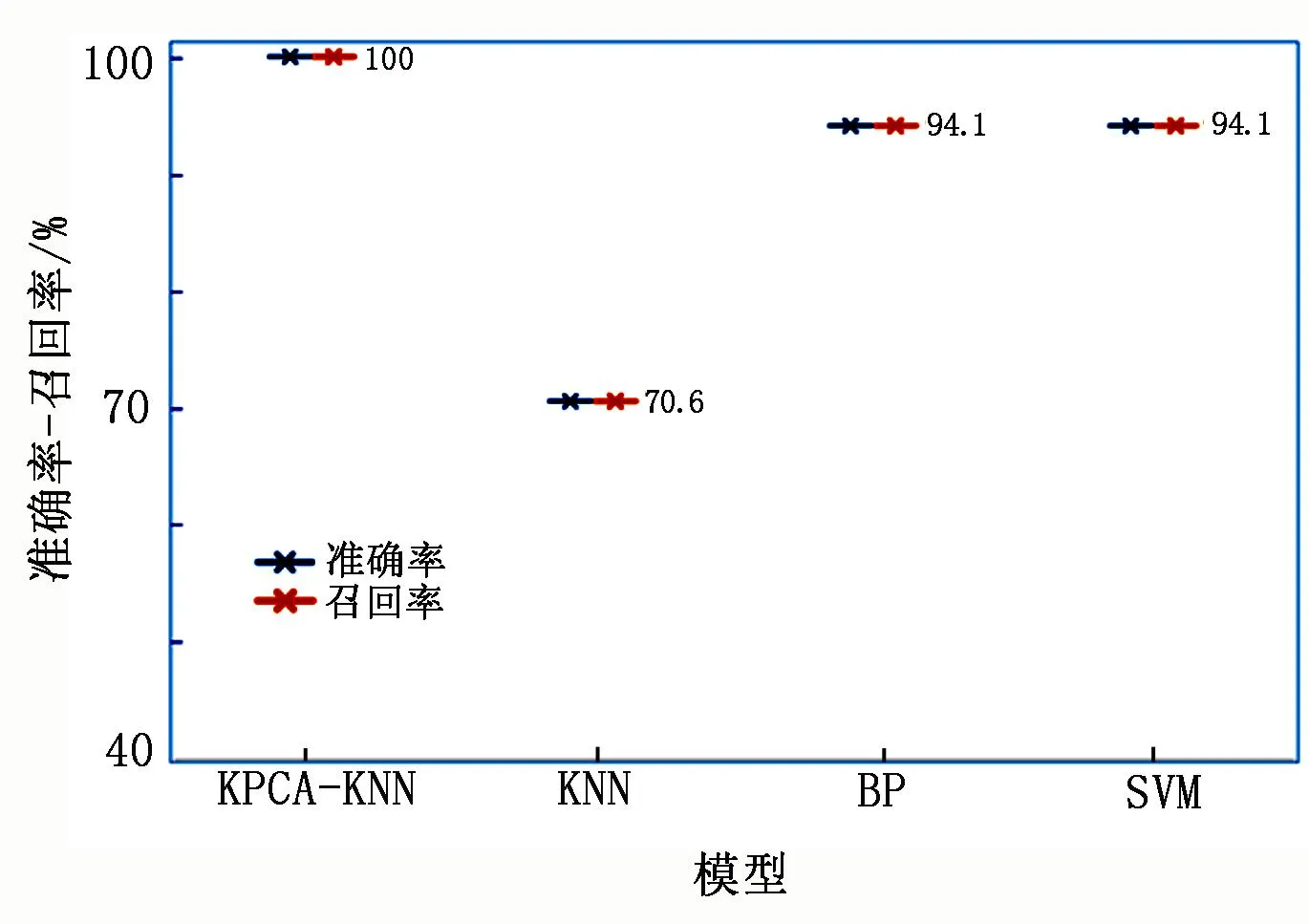
图5 准确率-召回率

各模型的F1-训练时间见图6。由图6可知,指标F1-score(同时考虑精确率和召回率,在0～1范围内,越靠近1表示效果越好)在本文模型预测中达到峰值1,且本文模型的训练时间为0.044 s,均短于其他3种模型。

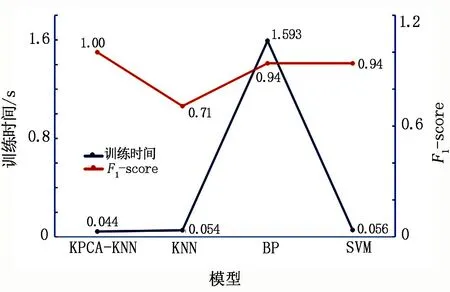
图6 F1-训练时间

综上,经过KPCA方法处理的数据可以提高KNN算法的准确率并缩短训练时间,是对原模型的进一步优化。

3 工程应用

选取6组国内外边坡实例进行稳定性预测[37],同时将预测结果与传统KNN、BP神经网络、SVM的预测结果进行对比,结果见表4。由表4可知,本文模型预测结果与实际边坡情况完全相符,其余3种对比模型均出现了错判(KNN错判2个,BP和SVM各错判1个)。由此可见,经过KPCA处理的KNN预测模型效果最好,进一步验证了本文模型的准确性和合理性。

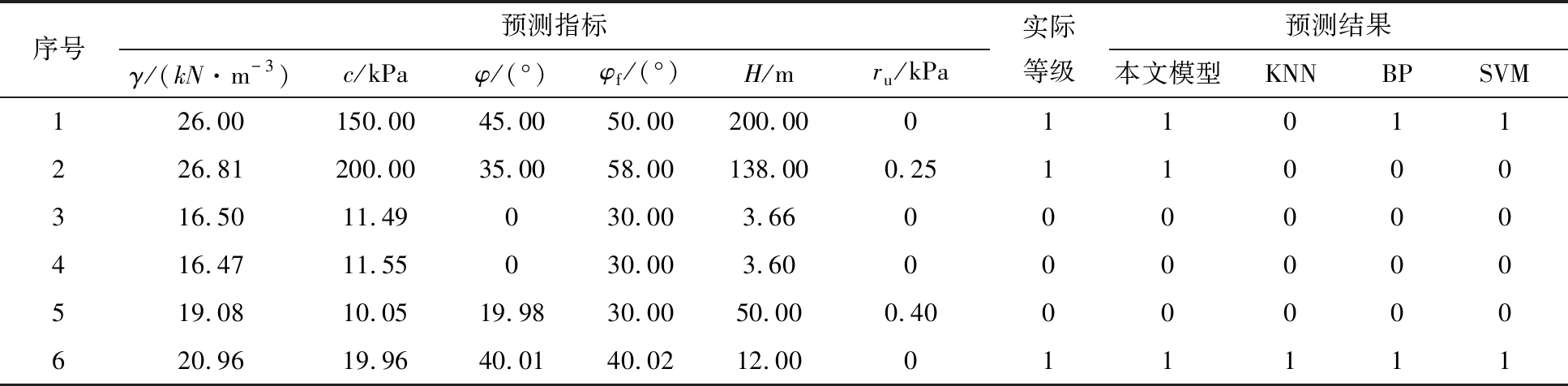
表4 预测结果对比

4 结论

a.本文以55组边坡实例样本为研究对象,选取容重、黏聚力、内摩擦角、边坡角、边坡高度、孔隙压力比作为边坡稳定性预测指标,并采用统一极差处理法对样本指标的原始数据进行处理,消除了指标量纲的影响。

b.运用核主成分分析将样本指标数据映射到高维空间进行线性运算,经过训练构建了KPCA-KNN边坡稳定性预测模型,模型测试集准确率和召回率均为100%,F1-score达到峰值1且训练时间短。

c.6组工程实例预测结果与边坡实际状态完全相符,且优于传统的KNN、BP神经网络、SVM模型,表明本文建立的KPCA-KNN模型是一种有效的边坡稳定性预测方法。在后续的工程应用中,可根据工程需要,基于MATLAB平台建立数据采集、数据预处理、质量控制和分析预测等一体化边坡稳定性实时监测系统,以实现边坡稳定性监测预警的智能化和可视化。