挠性剑杆织机变导程螺杆设计

迟连迅,詹雄烽,袁汝旺

(1.山东日发纺织机械有限公司,山东 聊城 252000; 2.天津工业大学 机械工程学院,天津 300387; 3.天津工业大学 天津市现代机电装备重点实验室,天津 300387)

剑杆织机可用于多种纤维材料织造,产品适应性广,剑杆驱动形式主要包括空间四连杆[1]、共轭凸轮[2]和变导程螺杆[3]等。变导程螺杆传剑机构具有传动链短与传递效率高等特点,变导程螺杆是控制剑杆运动特性的关键原件,影响剑杆织机的车速、幅宽和振动等性能参数。

国内外学者关于变导程螺杆传剑机构的研究主要集中在剑杆运动规律设计、传动系统建模与变导程螺杆的设计与制造等方面,如张雷等[4]基于改进梯形运动规律、蒋秀明等[5]基于椭圆比运动规律、袁汝旺等[6]基于傅里叶级数运动规律研究变导程螺杆传剑系统建模方法及剑杆运动特性;蔡军[7]构造的基于跃度连续的引纬运动方程不仅有效抑制剑杆振动而且简化计算过程;Kang等[8-9]、Lin等[10]基于空间坐标变换及啮合原理给出螺旋线与螺旋曲面的设计方程,并探讨变导程螺杆的4轴数控加工方法;张威等[11]对变导程螺旋传动中螺旋面的通用曲面进行建模,并对螺旋线过渡进行设计;杨客[12]利用ABAQUS对不同类型变导程螺旋副的滚子进行受力分析,但以上研究尚未系统性地对变导程螺旋引纬机构展开研究。

本文将引纬运动规律与后续螺杆设计方法相结合,考虑初始加速度对螺杆导程的影响,提出一种新型的螺杆设计方法。以曲柄转角作为唯一变量,提出变导程螺杆传剑机构建模方法及初始导程边界控制条件与调节方法,给出变导程螺旋线的设计方程,分析不同初始加速度对变导程螺杆曲线的影响,为实现不同幅宽织机螺杆系列化设计提供参考。

1 变导程螺旋引纬机构建模

1.1 工作原理

图1示出变导程螺旋引纬机构工作原理[12],变导程螺旋引纬机构由曲柄滑块机构串联变导程螺旋传动机构组成,其中曲柄“1”匀速转动,通过连杆“2”带动滑块“3”做往复直线运动,并通过螺旋副使得螺杆“4”往复摆动,剑带轮“5”安装在螺杆末端并驱动剑带往复直线运动。

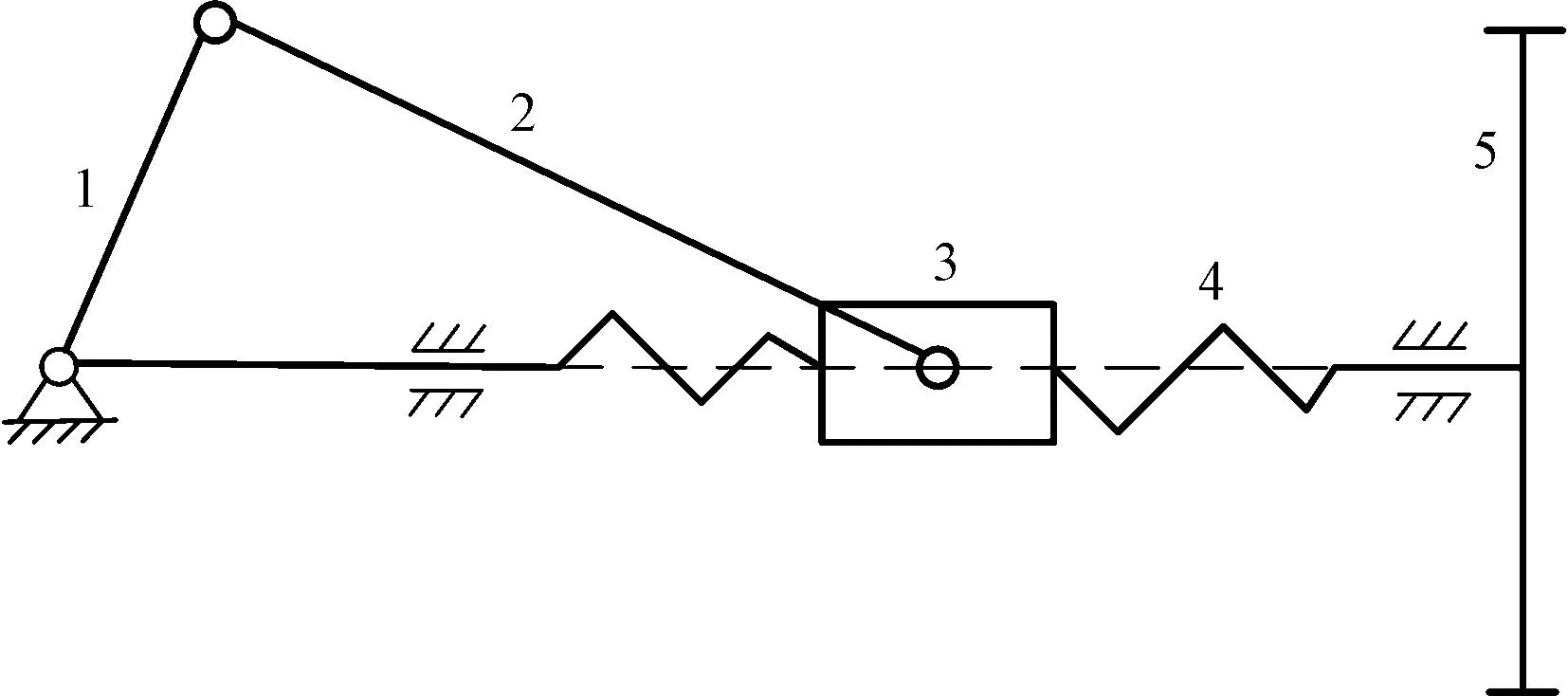
1—曲柄; 2—连杆;3—滑块;4—螺杆;5—剑带轮。图1 变导程螺旋引纬机构工作原理Fig.1 Schematic diagram of variable lead screw weft insertion mechanism

1.2 曲柄滑块机构建模

图2示出曲柄滑块机构运动简图,以O为原点建立坐标系xOy,由文献[13]可知,机构模型为式(1)～(3):

图2 曲柄滑块机构Fig.2 Crank slider mechanism motion diagram coordinate system

(1)

(2)

(3)

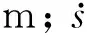
1.3 螺旋传动机构建模

由图1可知,滑块与螺杆通过运动副传动,滑块位移与螺杆转角关系为:

(4)

式中:θ为螺杆转角,rad;L为螺杆导程,m;s、θ、L均为曲柄转角φ1的函数。

令RL(φ1)=L(φ1)/2π,则

s(φ1)=RL(φ1)·θ(φ1)

(5)

分别求式(5)一阶导数和二阶导数可得:

(6)

(7)

由此可以得到螺杆的运动规律模型为:

(8)

(9)

(10)

1.4 剑杆运动规律模型

考虑剑杆运动速度、负向加速度峰值和纬纱交接平稳性等因素,选择椭圆比函数作为剑杆运动规律,其模型为:

(11)

式中:S为剑杆的位移,m;V为剑杆速度,m/s;A为剑杆加速度,m/s2;Sm为剑杆最大动程,m;k为椭圆比系数。

1.5 螺杆螺旋线方程

图3为螺杆螺旋线的示意图,剑杆位移S与螺杆转角的θ的关系为:

图3 螺杆螺旋线示意图及柱坐标系下螺杆螺旋线Fig.3 Screw spiral schematic diagram (a) and Screw helix in cylindrical coordinate system(b)

θ=S/R

(12)

式中:R表示剑带轮半径,m。

由式(8)可得:

(13)

当φ1=0时,s(φ1)=S(φ1)=0;

由洛必达法则可知:

(14)

即剑杆初始加速度不能为0。故螺旋线方程为:

(15)

2 结果与分析

表1为变导程螺旋引纬机构的基本参数,剑杆最大动程取2种,满足不同幅宽剑杆引纬差,其中S1、S2表示剑杆不同的最大动程。

表1 剑杆织机基本参数Tab.1 Motion parameters of rapier loom

2.1 曲柄滑块机构运动特性分析

图4为滑块归一化运动特性,当曲柄转角φ1=0°时,滑块位移和速度均为0,但具有一定的初始加速度;当曲柄转角φ1=180°时,滑块位移达到最大240mm,速度为0 m/s,加速度为负向最大值,但加速度变化较快,易引起剑杆端部振动,不利于纬纱平稳交接。若采用等导程螺杆设计,剑杆运动规律为滑块运动规律的等比例缩放,不利高速引纬需求,故可通过螺杆导程变化调节滑块运动规律不足,以满足引纬需求。

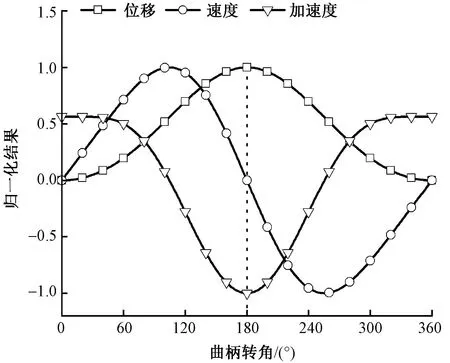
图4 滑块运动特性Fig.4 Motion law of slider

2.2 椭圆比系数对剑杆运动特性影响

为研究椭圆比系数对剑杆运动规律影响,取椭圆比系数k2=0、0.15、0.30、0.45,图5、6分别为k2取不同值时剑杆运动规律归一化速度和加速度的变化情况。当曲柄转角φ1=0°时,剑杆运动具有一定的初始加速度,且随着椭圆比系数k2的增加,初始加速度逐渐减小;当曲柄转角φ1=180°时,负向加速度达到最大,但负向加速度随椭圆比系数k2增加呈现变化平缓到变化剧烈的过程,当k2=0.30时,加速度变化平缓,振动较小,利于纬纱交接。

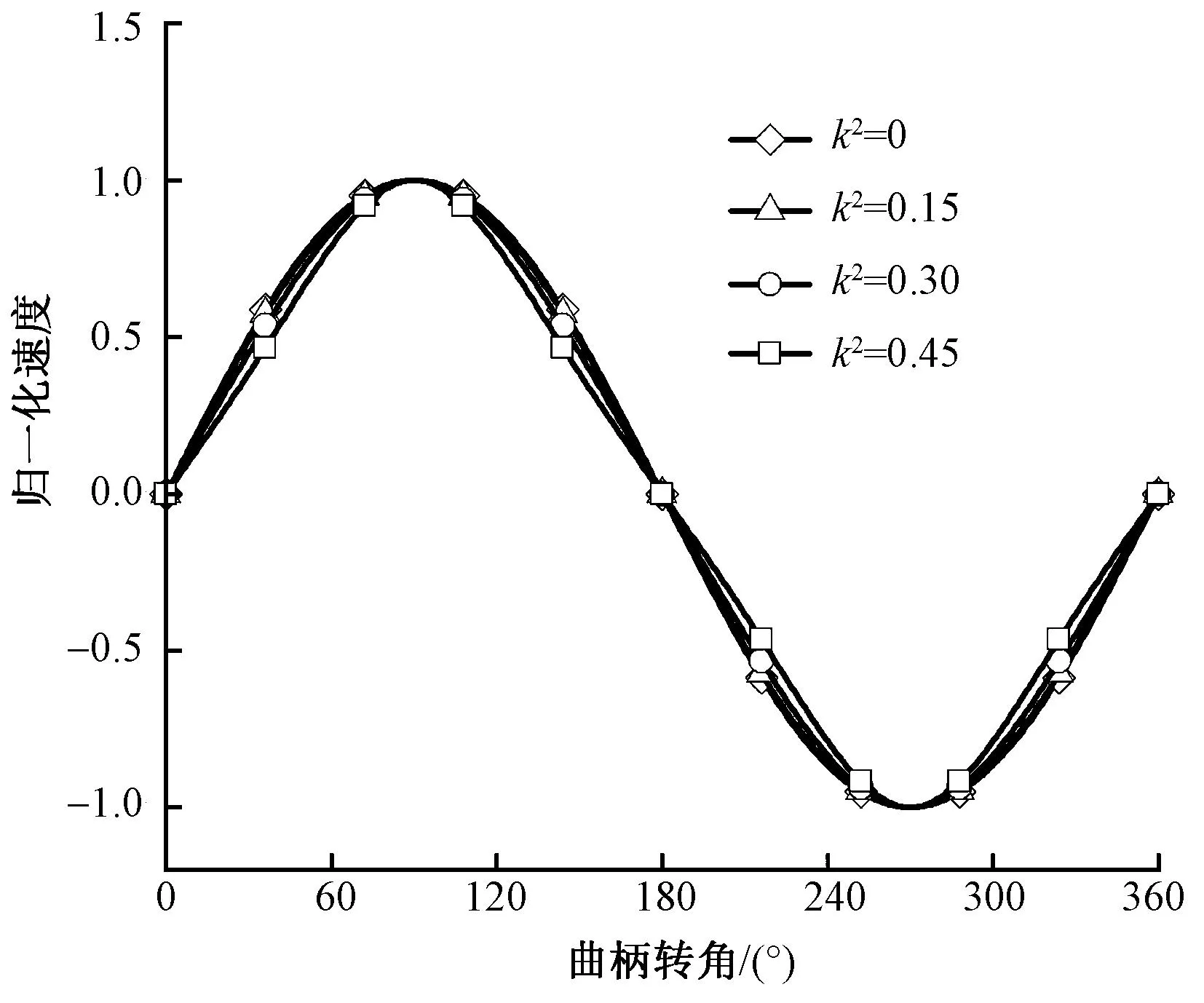
图5 不同椭圆比系数对剑杆速度的影响Fig.5 Influence of different elliptic ratio coefficients on the speed of the rapier

图6 不同椭圆比系数对剑杆加速度的影响Fig.6 Influence of different elliptic ratio coefficients on the acceleration of the rapier

2.3 螺杆变导程曲线

图7、8分别为椭圆比系数k2=0、0.15、0.30、0.45且取剑杆最大动程S1max=1 920mm、S2max=2 245mm时螺杆导程变化情况。导程关于φ1=180°对称分布;在φ1∈[0, 180°]范围内,随着椭圆比系数k2增加,导程函数由单调增函数逐渐变化为非单调函数,导程函数波动大,不利有后续螺杆加工制造;当曲柄转角φ1=0°时,随着椭圆比系数k2增加,初始螺杆导程增加,且随着剑杆最大位移Smax增加,初始导程函数逐渐减小;当k2∈[0.15, 0.30]时,导程函数的单调性发生变化,故应合理选择椭圆比系数k2并控制螺杆初始导程,调节初始导程和最大导程差值。

图7 k2对螺杆导程的影响(S1max=1 920mm)Fig.7 Lead variation by k2 on S1max=1 920mm

图8 k2对螺杆导程的影响(S2max=2 245mm)Fig.8 Lead variation by k2 on S2max=2 245mm

取椭圆比系数k2=0.20,螺杆中径24mm可以得到,当S1max=1 920mm时,变导程螺杆初始导程为108.6mm,最大导程为149.2mm,导程变化率为27.2%;当S2max=2 245mm时,变导程螺杆初始导程为92.8mm,最大导程为127.6mm,导程变化率为27.3%。图9、10分别示出k2=0.20,S1max=1 920 mm和S2max=2 245 mm时螺杆的螺旋线,可见螺旋线连续光滑。选择图10螺旋线(S2max=2 245mm)进行加工制造获得的变导程螺杆如图11所示。某型剑杆织机运用该变导程螺杆,运转车速550 r/min,变导程螺杆传剑机构运转平稳,纬纱交接可靠,机器振动噪声小。采用本文方法可设计适配不同幅宽的螺杆。

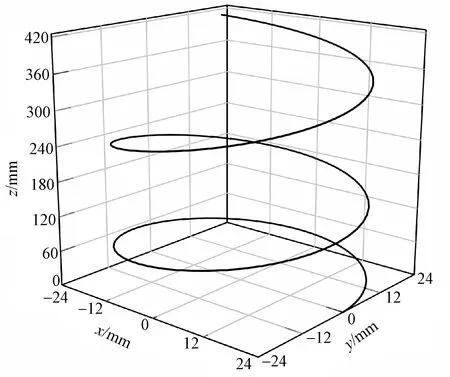
图9 变导程螺杆螺旋线(S1max=1 920mm)Fig.9 Variable lead screw helix (S1max=1 920mm)

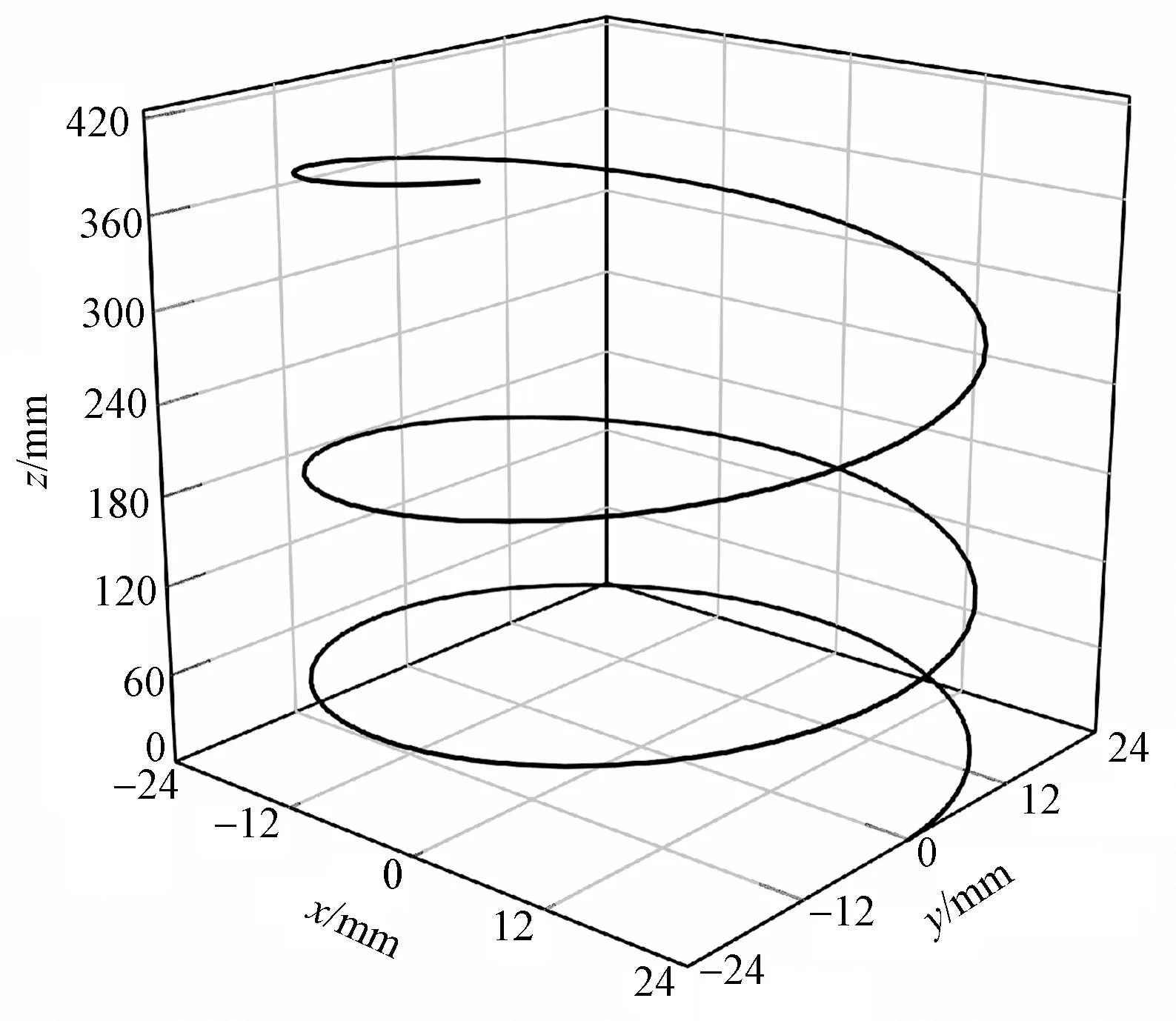
图10 变导程螺杆螺旋线(S2max=2 245mm)Fig.10 Variable lead screw helix (S2max=2 245mm)

图11 变导程螺杆实例Fig.11 Variable lead screw example

3 结 论

本文以曲柄转角作为唯一变量,提出变导程螺杆传剑机构建模方法及初始导程边界控制条件与调节方法,并给出变导程螺旋线的设计方程。选取椭圆比函数作为剑杆运动规律,分析不同椭圆比系数对剑杆初始加速度及变导程螺杆导程曲线的影响。结果表明:剑杆初始加速度不能为0,随着椭圆比系数增加,导程函数初始值增加,但升程阶段导程函数为呈现非单调性变化,对应椭圆比系数范围为k2=0.15～0.3;当椭圆比系数k2=0.2时,2种不同幅宽所对应螺杆导程变化率均约为27%。