分布卷积上的Levi-Civita联络
刘思瑶,王 勇
(东北师范大学数学与统计学院,吉林 长春 130024)
1 预备知识

定义1.1[1]若X,Y,Z∈Γ(M),则满足
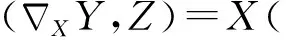
(1)
定义1.2[2]若M上的切向量丛TM存在子丛D,且当X,Y∈Γ(D)时,满足[X,Y]∉Γ(D),则称D∈Γ(M)为不可积分布.同理,当X,Y∈Γ(D)时,满足[X,Y]∈Γ(D),则称D∈Γ(M)为可积分布.
由M上的ɡ可以得到分布D上的度量张量场ɡD.令D⊥∈Γ(M)为D的正交分布,则存在度量张量场ɡD⊥,且满足ɡ=ɡD+ɡD⊥.
对于X,Y∈Γ(M),定义:
(2)
其中πD:TM→D和πD⊥:TM→D⊥为投射.
定义1.3[3]若X1,X2∈Γ(D),Y∈Γ(D⊥),满足
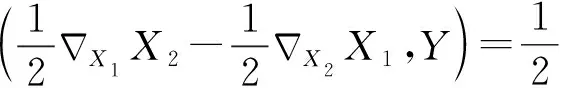
(3)
ɡ(A(X1,X2),Y)=-ɡ(A(X1,Y),X2),
(4)
则称此(1,2)型光滑张量场A为可积张量.
定义1.4[4]令(M,ɡM)和(N,ɡN)为伪黎曼流形,f:M→为光滑函数.由M×N及度量张量ɡM⨁f2ɡN构成的积流形称为卷积,记作M×fN.
定义1.5[2]令(M,ɡM)和(N,ɡN)为伪黎曼流形且TM=D1⨁D1,⊥,TN=D2⨁D2,⊥.f:M→为光滑函数,πM:M×N→M和πN:M×N→N为投影.令:

(5)
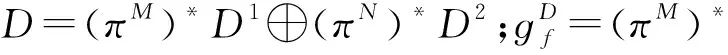
(6)



(7)
定义1.7[5]若X1,X2,X3∈Γ(D),都满足Rf,D(X1,X2)X3=0,则称曲率张量Rf,D是平坦的.
定义1.8[2]若X1,X2∈Γ(D),定义D上的Ricci张量为
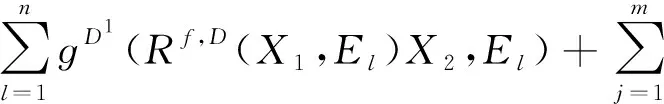
(8)

定义1.9 定义D上的数量曲率为
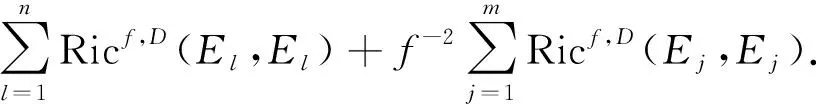
(9)
定义1.10[2]若X1,X2∈Γ(D),满足
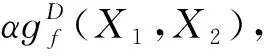
(10)

2 主要结果
性质2.1 若X1,X2∈Γ(D1),Y1,Y2∈Γ(D1,⊥),U1,U2∈Γ(D2),V1,V2∈Γ(D2,⊥),则:
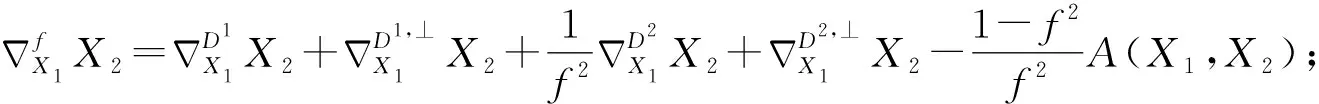


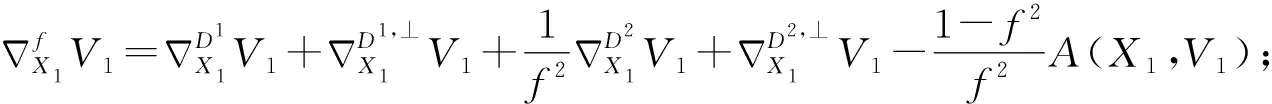


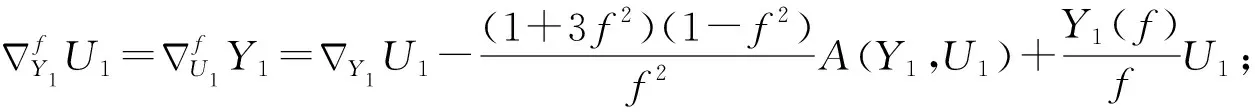
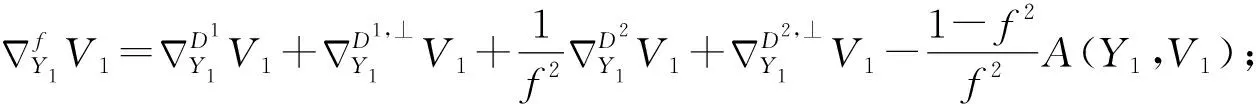
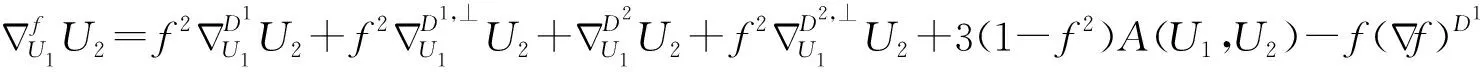
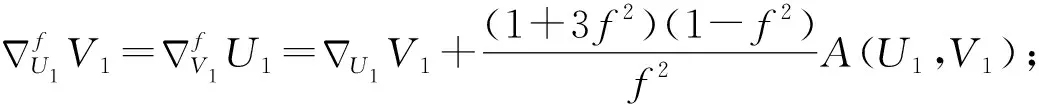



性质2.2 若X1,X2∈Γ(D1),U1,U2∈Γ(D2),则:


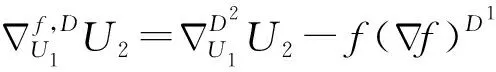
性质2.3 若X1,X2,X3∈Γ(D1),U1,U2,U3∈Γ(D2),则:
(1)Rf,D(X1,X2)X3=RD1(X1,X2)X3;

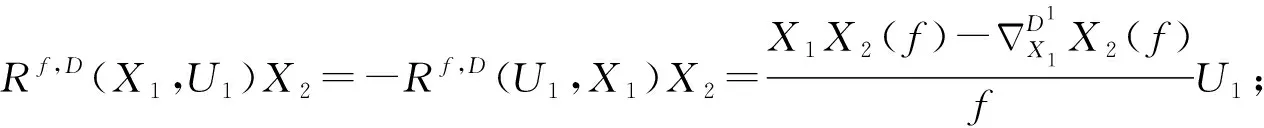
(4)Rf,D(U1,U2)X1=0;
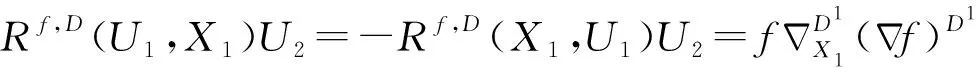

性质2.4 若X1,X2∈Γ(D1),U1,U2∈Γ(D2),则:

(2) Ricf,D(X1,U1)=Ricf,D(U1,X1)=0;

性质2.5D上的数量曲率为

定理2.1 若曲率张量Rf,D是平坦的,则D1为可积分布.
证明若曲率张量Rf,D是平坦的,则满足[X1,X2]D1,⊥(f)=0,其中X1,X2∈Γ(D1).故[X1,X2]=[X1,X2]D1+[X1,X2]D1,⊥=[X1,X2]D1∈Γ(D1).
3 例子
例3.1 令M=,则有:
f:→,ɡD2⨁(πN)*ɡD2,⊥,
(11)
D=(πM)*(T)ɡD2.
(12)

性质3.1 若∂t∈Γ(T),U1,U2∈Γ(D2),V1,V2∈Γ(D2,⊥),则:
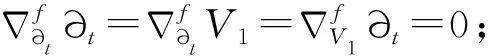
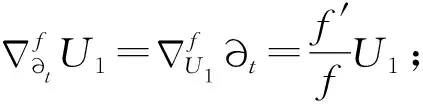
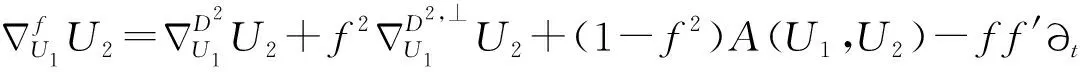

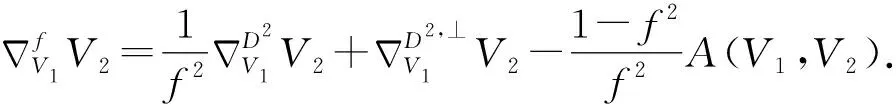
性质3.2 若∂t∈Γ(D1),U1,U2∈Γ(D2),则:
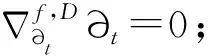

性质3.3 若∂t∈Γ(D1),U1,U2,U3∈Γ(D2),则:
(1)Rf,D(∂t,∂t)∂t=Rf,D(∂t,∂t)U1=Rf,D(U1,U2)∂t=0;
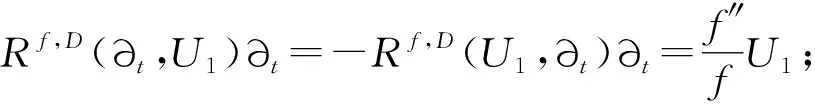

(4)Rf,D(U1,U2)U3=RD2(U1,U2)U3-(f′)2(ɡD2(U2,U3)U1-ɡD2(U1,U3)U2).
性质3.4 若∂t∈Γ(D1),U1,U2∈Γ(D2),则:

(2) Ricf,D(∂t,U1)=Ricf,D(U1,∂t)=0;
(3) Ricf,D(U1,U2)=RicD2(U1,U2)+[(m-1)(f′)2+ff″]ɡD2(U1,U2).
性质3.5D上的数量曲率为
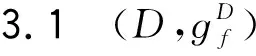


(3)αD2+(m-1)(f′)2+ff″=αf2.
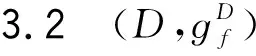

例3.2 令

(13)
f:M→,ɡD1⨁f2(πN)*ɡD2.
(14)
性质3.6 若X1,X2∈Γ(D1),U1,U2∈Γ(D2),则:


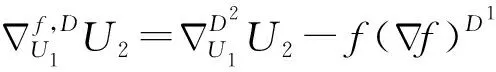
性质3.7 若X1,X2,X3∈Γ(D1),U1,U2,U3∈Γ(D2),则:
(1)Rf,D(X1,X2)X3=RD1(X1,X2)X3;

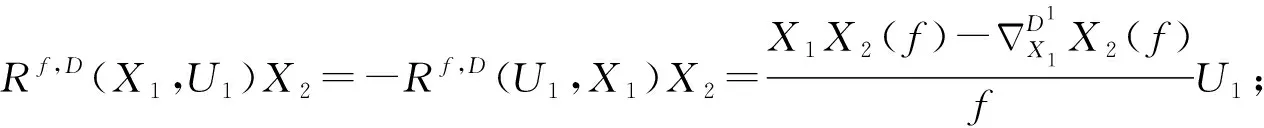
(4)Rf,D(U1,U2)X1=0;
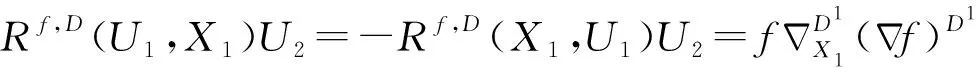

性质3.8 若X1,X2∈Γ(D1),U1,U2∈Γ(D2),则:

(2) Ricf,D(X1,U1)=Ricf,D(U1,X1)=0;

性质3.9D上的数量曲率为


