随机连续搅拌釜式反应器模型的动力学行为
杨 颖,李 芳
(长春师范大学数学学院,吉林 长春 130032)
1 预备知识
本文将文献[1]中关于等温自催化反应连续搅拌釜式反应器(CSTR)模型加入随机扰动,构建合适的随机模型并研究其性质.在给出随机模型之前,回顾一下CSTR模型丰富的动力学行为,其反应机制可以分为以下2步反应:
A+2B→3B(K1)(三分子),
B→C(K2).
这里:A,B是反应物;C是某种惰性产物.
原型三分子自催化反应A+2B→3B构成了表现出“奇异”行为的最简单齐次系统.由于A和B的浓度不是相互独立的,所以该反应是单变量系统.但在化学反应计量学中,A→B的反应只与进口流的成分有关.如果B的流入量b0不是很大的话,系统会呈现多样性.
在自催化剂B不是无限稳定的情况下,B→C的这种行为在经历一级衰变(或中毒)的情况下更加丰富.尽管催化剂B是无限稳定的,但它们却表现出停留时间范围,在该范围内存在不同的稳定态和唯一解的范围,即使在充分搅拌、等温、开放的条件下,也可以发现多重稳定、熄灭、滞后、点火等性质和来回弛豫时间.
将化学反应速率和流入、流出率联系起来的质量平衡方程为
(1)
这里a0和b0分别是反应物A和B在进口流的浓度.本文利用与文献[1]类似的方法作无量纲化变换.令α=a/a0,β=b/a0,τres=1/kf为平均停留时间,这样方程(1)变为如下的无量纲形式:
(2)


(3)
通过(3)式,系统降为1维,αss是下面三次方程的根:
(4)
文献[1]利用分歧理论的方法指出:系统(2)在任何给定的停留时间可能有3种平衡状态α1≥α2≥α3,并且可能有9种不同性质的结构.由3种平衡状态的稳定性可以产生很多不同的动力学结构:最小解α1,中间解α2和最大解α3.
对于进水中无催化剂流入的特殊情况,即b0=0时,最小解α1始终是稳定的;中间解α2始终是不稳定的;最大解α3的稳定性则随催化剂的稳定性和停留时间而变化.
当流入的催化剂浓度不为零,即b0>0时,最小解α1可能是结点或者焦点,并且可能变得不稳定;中间解α2总是一个鞍点;稳定状态α3的最上面的那支可能被一个稳定或不稳定的极限环包围,表现为稳定或不稳定的结点或焦点.
最近,文献[2-5]讨论了一些带有随机扰动的化学反应模型,并且得到了很好的结果.本文在系统(1)中加入白噪声,得到如下的随机CSTR系统:
(5)

在本文中,令(Ω,F ,{Ft}t≥0,P)是带有域流{Ft}t≥0的完备概率空间,满足通常的条件,即它是右连续的、F0包含所有的P-零集.记
(6)
已有工作中随机系统(5)还未曾被研究过.本文将证明随机CSTR模型正解的存在唯一性,并进一步证明随机系统(5)具有遍历性和平稳分布,并通过数值模拟来验证本文的理论结果.
2 正解的存在唯一性
随机CSTR模型(5)的解是正的和全局的,这对于研究模型(5)的遍历性是很必要的.
定理2.1 如果σ1,σ2满足
(7)
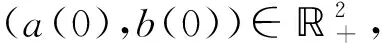

或
max{a(t),b(t)}≥m}.

换句话说,为了完成证明,需要说明τ∞=∞.用反证法.如果假设这个断言是错误的,则存在常数T≥0和ε∈(0,1),使得
P{τ∞≤T}>ε,
从而存在一个整数m1≥m0使得对于所有的m≥m1,有
P{τm≤T}≥ε.
(8)


LVdt+σ1(a-1)dB1(t)+σ2(b-1)dB2(t)+C(a+b)(σ1adB1(t)+σ2bdB2(t)).
(9)
这里L是系统(5)的生成算子,并且
(10)
根据条件(7),以下两个不等式同时成立:
令
进一步可得
其中K是一个正常数.因此

对上式取期望得

(11)


由(8)和(11)式得
V(a(0),b(0))+KT≥E[IΩm(ω)V(a(τm),b(τm))]≥εf(m),
这里IΩm(ω)是Ωm的示性函数.
当m→∞时,
∞>V(a(0),b(0))+KT=∞,
矛盾.因此τ∞=∞,a.s..
3 遍历性
设X(t)是由随机方程描述的El(El表示欧几里得l-空间)中的齐次马尔可夫过程,X(t)的扩散矩阵为
随机微分方程描述为
(12)
结合方程(12)定义一个微分算子L,
引理3.1[7-8]假设存在具有如下性质的带正则边界Γ的有界域U⊂El,满足:
(B1) 在U和它的一些邻域,扩散矩阵Λ(x)的最小特征值λ(x)非0;

则马尔可夫过程X(t)存在平稳分布kf(·).令f(·)是关于测度kf可积的函数,则对所有的x∈El,有下面的公式成立:
注1 引理3.1的证明由文献[7]给出.文献[7]定理4.1和引理9.4给出了具有密度平稳分布的存在性;定理5.1和定理7.1得到了弱收敛性和遍历性.为了验证条件(B1),只需要证明F在任何有界域U上一致椭圆即可,其中
即存在一个正数M,使得下式成立:

由文献[9]和瑞利原理[10]即可知上式成立.为了验证条件(B2),只需证明存在某个邻域U和一个非负的C2-函数,使得对于任意的ElU,LV<0[11].
引理3.2 设X(t)为El中的正则自治马尔可夫过程.如果X(t)相对于某个有界域U是常返的,那么它相对于El中的任一非空区域也是常返的.


证明为了证明该结论,只需证明条件(B1)和(B2)满足即可.随机系统(5)的扩散矩阵为
从而系统(5)可改写成如下形式:
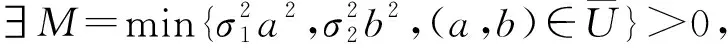

从而引理3.1中的条件(B1)满足.

定义C2-函数V:

令
则有
(13)
记
其中ε是使得下面不等式同时成立的充分小的正数:
(14)
(15)
(16)
(17)
令
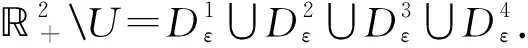

从而由(14)式有LV≤-1.
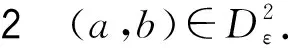
因此由(13)和(15)式可得LV≤-1.

因此由(13)和(16)式可得LV≤-1.

由(13)和(17)式可得在这个区域上有LV≤-1.
对上述4种情况的讨论表明,引理3.1中的条件(B2)满足.定理3.1证毕.
4 数值模拟
使用离散化的方法,选取Δt=0.002.在文献[1]中,τres=1/kf是一个非常重要的参数,因为其值的变化会导致确定系统(1)稳态的多样性.
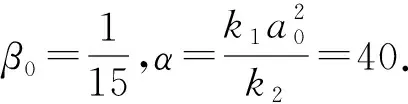
在模型(5)中选取以下3组参数:
k1=0.4,k2=0.022 5,kf=0.005 263 16(τres=190),a0=1.5,b0=0.1;
(18)
k1=0.4,k2=0.022 5,kf=0.004(τres=225),a0=1.5,b0=0.1;
(19)
k1=0.4,k2=0.022 5,kf=0.003 174 6(τres=315),a0=1.5,b0=0.1.
(20)
总是选取σ1=0.5,σ2=0.5.
例4.1 选取参数为(18)式所示,系统(1)的相平面呈现出盘旋至稳定焦点的轨道.系统最开始时远离奇点,但是经历了一系列的阻尼振荡后逐渐向其趋近,模拟结果如图1—2所示.

(a)确定性模型(1) (b)随机模型(5)图1 选取参数为(18)式所示时系统的散点分布比较图

图2 参数选取为(18)式所示时,随机系统的解及其柱状图
例4.2 选取参数值为(19)式所示,系统(1)的相平面对应于一个围绕着不稳定焦点的稳定极限环,并且x和y呈现持续的无阻尼振荡,在经历了初始时刻的“沉降”之后,变成了具有恒定频率和振幅的脉冲.在x-y的相平面中,系统退绕到包围不稳定焦点的闭合曲线.模拟结果如图3—4所示.

(a)确定性模型(1) (b)随机模型(5)图3 选取参数为(19)式所示时系统的散点分布比较图
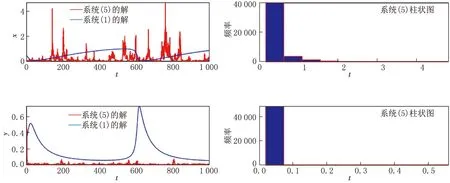
图4 参数选取为(19)式所示时随机系统的解及其柱状图
例4.3 选取参数为(20)式所示时,振荡是发散的.系统越过鞍点边界,在低反应性的稳定结点上稳定下来.在x-y相平面上,这个分支由鞍点和稳定极限环的组合来表示.模拟结果如图5—6所示.
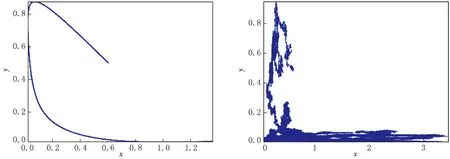
(a)确定性模型(1) (b)随机模型(5)图5 选取参数为(20)式所示时系统的散点分布图

图6 参数选取如(20)式所示时随机系统的解及其柱状图
让人觉得很有趣的是,确定性模型(1)的3个平衡点9种性态,无论其表现出什么样的动力学行为,相应的随机模型(5)只需要满足条件(7)中对白噪声强度的限制条件,就总是具有平稳分布和遍历性.

