一类Block型李代数的2-局部导子
肖明月,唐孝敏
(黑龙江大学数学科学学院,黑龙江 哈尔滨 150080)
0 引言
李代数及其相关课题已经成为数学研究中的重要领域之一.李代数是一类非常重要的非结合代数,源于对李群的研究,后经相关学者对复数域上的有限维半单李代数有了更为深入且全面的研究,构建了经典的理论体系,奠定了理论基础.导子在研究李代数结构理论体系中起着非常重要的作用,学者们在研究过程中进一步扩充了导子结构.1997年,emrl引入了2-局部导子[1]的概念,2-局部导子为导子概念的非线性推广,此后学者们相继对代数的2-局部导子进行了大量的研究.关于李代数的2-局部导子问题的研究主要是判断其2-局部导子是否为导子[2-6].
Block型李代数[7]在1958年由Block引入,Block型李代数在数学及物理学科上有着广泛的应用,起着极其重要的作用,大量重要的无限维李代数都与其有着颇多相似之处,吸引了众多研究者的关注.在Block型李代数的众多研究成果主要集中在Block型李代数的结构和表示理论[8-10]方面,但关于Block型李代数局部性质的研究还很少.本文主要致力于研究一类Block型李代数的2-局部导子,确切地说,本文研究的Block型李代数如下:
Block型李代数B(q),q∉,具有基{Lm,i|m,i∈},李括号如下:
[Lm,i,Ln,j]=(n(i+q)-m(j+q))Lm+n,i+j,∀m,n,i,j∈.
1 预备知识
本文约定L是一个李代数.给出一些基本的定义和一些引理.
定义1 设D为L上的线性变换,若D满足
D([x,y])=[D(x),y]+[x,D(y)],∀x,y∈L,
则称D为导子.记所有L的导子构成的集合为Der(L).对任意a∈L,映射
ad(a):L→L,x→[a,x],∀x∈L
是导子,这种形式的导子称为内导子.记所有L的内导子构成的集合为Inn(L).
定义2 设Δ是L上的一个线性变换(不一定是线性的).若对任意的x,y∈L,都存在L的一个导子Dx,y,使得Δ(x)=Dx,y(x)且Δ(y)=Dx,y(y),那么称Δ是L的一个2-局部导子.
引理1[11]Der(B(q))=Inn(B(q))⨁∂2,其中∂2是B(q)的一个外导子且满足:
∂2:Lm,i→iLm,i,∀m,i∈.
由引理1,易得如下引理:
引理2 设Δ是L上的一个2-局部导子.若任意x,y∈B(q),存在Dx,y使得Δ(x)=Dx,y(x),且Δ(y)=Dx,y(y),则Dx,y可写成
其中:am,i(x,y),λ(x,y)∈;m,i∈.
2 Block型李代数2-局部导子
本节Δ是Block型李代数B(q)上的一个2-局部导子,∂2是Block型李代数的一个外导子.给出关于Block型李代数2-局部导子的主要结果:
定理1 Block型李代数上的2-局部导子是导子.
为了证明这个定理,需要以下几个引理.
引理3 设Δ是B(q)上的2-局部导子,则对任意y∈B(q),有:
(ⅰ) 对于n∈*,j∈,若Δ(Ln,j)=0,则
(1)

(ⅱ) 对于j∈,若Δ(L0,j)=0,则
(2)
其中:a0,i(L0,j,y),λ(L0,j,y)∈;
证明(ⅰ) 由引理2,设
其中am,i(Ln,j,y),λ(Ln,j,y)∈.
因为Δ(Ln,j)=0,则有
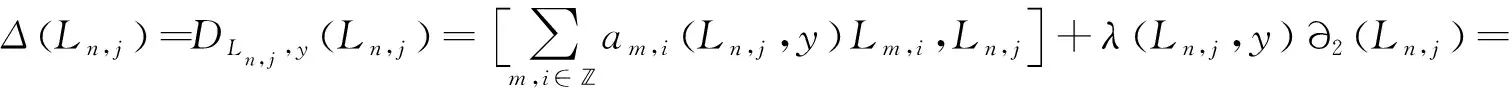
比较Ln,i+j,Ln,j,Lm+n,i+j的系数,可得:
n(i+q)a0,i(Ln,j,y)=0,i∈*,n∈*,j∈;
nqa0,0(Ln,j,y)+jλ(Ln,j,y)=0,n∈*,j∈;
(n(i+q)-m(j+q))am,i(Ln,j,y)=0,m,i∈,n∈*,j∈.
综上,

(ⅱ) 由引理2,设
其中am,i(L0,j,y),λ(L0,j,y)∈.
因为Δ(L0,j)=0,则有

比较Lm,i+j,L0,j的系数,则可得当m≠0时,am,i(L0,j,y)=0;当j≠0时,λ(L0,j,y)=0.结论得证.
引理4 设Δ是B(q)上的2-局部导子,使得Δ(L0,0)=Δ(L1,0)=0.则有Δ(Ln,j)=jξLn,jLn,j,∀n,j∈,其中ξLn,j=λ(L1,0,Ln,j)∈.
证明易知
(3)
(4)

令y=Ln,j,则由(3)和(4)式可得
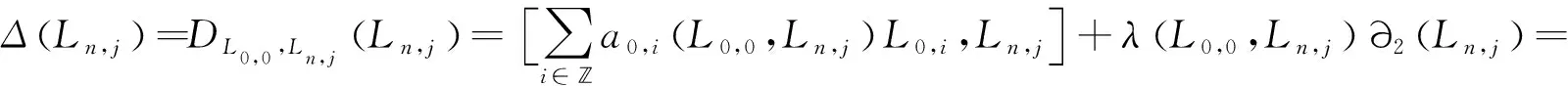
(5)
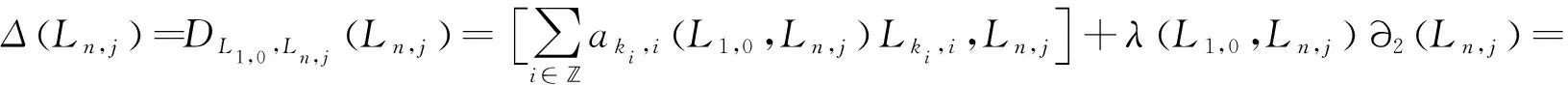
(6)
比较(5)和(6)式有
(n(i+q)-ki(j+q))aki,i(L1,0,Ln,j)=0.
从而Δ(Ln,j)=jλ(L1,0,Ln,j)Ln,j.令λ(L1,0,Ln,j)=ξLn,j,则结论得证.

证明因为Δ(L0,0)=Δ(L1,0)=0,由引理4可知Δ(Ln,0)=0,n∈*.再由引理3得
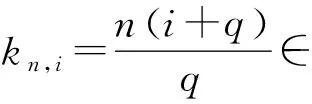
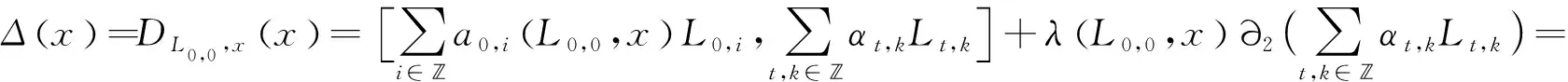

因为t是有限项的,所以可以找到足够大的n∈*,使得αkn,i+t,i+k=0,t,i,k∈,其中*.比较Lkn,i+t,i+k的系数,可得
(t(i+q)-kn,i(k+q))αt,kakn,i,i(Ln,0,x)=0,

引理6 设Δ是B(q)上的2-局部导子,使得Δ(L1,0)=0.则对任意的p∈*,y∈B(q),都存在,使得
证明因为Δ(L1,0)=0,由引理3可得
其中a0,i(L0,1,y)∈.设tp=L0,P+L0,2P,并令y=tp,则有
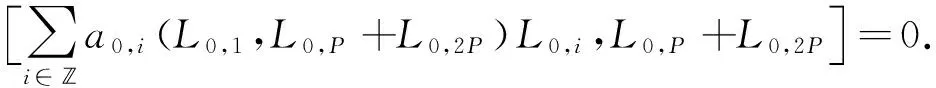
因为Δ(tp)=0,由引理2可设
其中am,i(L0,p+L0,2p,y),λ(L0,p+L0,2p,y)∈.
由于Δ(tp)=0,则可得
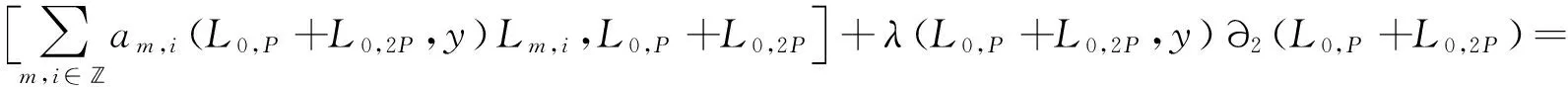
比较L0,p,L0,2p,Lm,i+p,Lm,i+2p的系数,则可得λ(L0,p+L0,2p,y)=0.当m=0时,可得Δ(tp)=0.当m≠0时,有
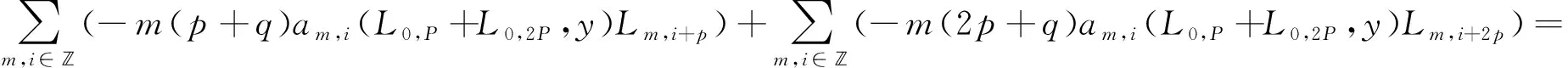
因为上式是有限项,又由上式可得
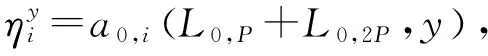
引理7 设Δ是B(q)上的2-局部导子,使得Δ(L0,0)=Δ(L1,0)=Δ(L0,1)=0.则∀x∈B(q)有Δ(x)=0.
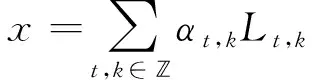
(7)
又因为Δ(L0,1)=0,则∀p∈*,由引理6可知
从而

将之与(7)式做比较,可得
(8)
因为ξx的取值不同,分为2种情况进行讨论.
情况1ξx=0.则由(7)式可知Δ(x)=0.
情况2ξx≠0.则需要证明{αt,k}=0,其中t,k∈且t=k时k≠0.
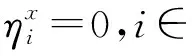
ξxkα0,k=0,
(9)
因为{αt,k}t,k∈是有限项,则存在b0∈,使得αt,k+b0i0=0.令k=k+bi0,其中b=1,2,…,b0-1,则有:
(10)
⋮ ⋮
由(10)式可知当t≠0时,有{αt,k}t∈*,k∈=0.再由(9)式可知k≠0时,有{α0,k}k∈*=0.综上可知{αt,k}=0,其中t,k∈且t=k时k≠0.又因为由(8)式可得Δ(α0,0L0,0)=0,则有Δ(x)=0.
定理1的证明Δ是B(q)上的2-局部导子,取导子DL0,0,L1,0,使得
Δ(L0,0)=DL0,0,L1,0(L0,0),Δ(L1,0)=DL0,0,L1,0(L1,0).
令Φ1=Δ-DL0,0,L1,0,则Φ1是2-局部导子,使得Φ1(L0,0)=Φ1(L1,0)=0.
由引理4可知Φ1(L0,1)=ξL0,1L0,1,其中ξL0,1∈.令Φ2=Φ1-ξL0,1∂2,则Φ2是2-局部导子,使得
Φ2(L0,0)=Φ1(L0,0)-ξL0,1∂2(L0,0)=0-0=0,
Φ2(L1,0)=Φ1(L1,0)-ξL0,1∂2(L1,0)=0-0=0,
Φ2(L0,1)=Φ1(L0,1)-ξL0,1∂2(L0,1)=ξL0,1L0,1-ξL0,1L0,1=0.
由引理7可知,Φ2=Δ-DL0,0,L1,0-ξL0,1∂2≡0,则Δ=DL0,0,L1,0+ξL0,1∂2是导子,结论得证.

