V-H荷载作用下海洋平台吸力式桩桶桩土承载特性研究
蒋建平,孙宏涛,高嘉若
(上海海事大学 海洋科学与工程学院,上海 201306)
近些年,海洋平台作为对海洋资源开采的主要建筑设施而被广泛应用。海洋平台位于海平面上,长年受到各种风浪荷载的侵蚀作用而易发生失稳现象,为解决这种意外的发生,对海洋平台基础的研究就显得尤为重要。目前,浅海区域的海洋平台基础有多种形式,其中主要的有重力式基础、单桩基础和桶形基础。重力式基础一般为钢筋混凝土沉箱结构,优点在于其结构形式较为简单,对于风浪荷载的抵抗性能较好,适用于砂土、岩土地基;缺点在于施工周期较长,且因施工环境在海平面,安装过程有所不便。世界上早期的海洋平台均采用重力式基础,如丹麦的Vindeby、瑞典的Lillgrund Oresund、比利时的Belwind 等[1]。单桩基础多指单根钢管桩基础,优点在于结构自重较轻、造价较低,安装程序简单且无需对浅海海床进行预先准备,既适用于软土地基,也适用于岩石地基;缺点在于对海床土体扰动较大,且施工过程中需考虑各种海洋荷载对打桩的影响以免出现误差。桶形基础也称为吸力式桩桶基础,可分为单桶或多桶形式,适用于浅海或深海地质条件为砂土或黏土的海域,原理是利用桶内外的压力差将桩桶贯入海床内进行打桩,由于吸力式桩桶安装、移动过程较为灵活,造价成本较低,经过多年的发展,其实用性和便捷性已经得到了海洋工程界的广泛认可。但对于吸力式桩桶的研究,相比其他基础而言还处于初步发展阶段,如中国的三峡响水海上风电场、三峡大丰海上风电场、阳江沙扒1期、5期海上风电场等[2]。
目前,吸力式桩桶与土相互作用的研究主要有以下3种方法:理论分析法、试验分析法和有限元分析法。理论分析法主要分为弹性理论法和地基反力法,弹性理论法是利用弹性理论的原理来探讨吸力式桩桶在受到荷载时桩土之间作用力与位移之间的关系,地基反力法主要有极限分析法、弹性分析法和复合分析法,其中复合分析法又称为p-y曲线法。Mcclelland 和Focht[3]第一次提出p-y曲线法,并进行了土固结不排水三轴试验,提出了计算桩土之间抗力的方法。程泽坤[4]基于p-y曲线法对横向力作用下高桩结构物的实施方法、特点进行了研究,并编制了相应的程序。戴国亮等[5]基于p-y曲线法,对考虑土体流变效应的吸力式沉箱基础进行研究,结果显示长期水平荷载下考虑时间因素的p-y曲线计算结果能较好地吻合模型试验值。周建武[6]采用新旧API规范中计算砂土的两种p-y曲线方法,与工程实例进行对比分析来得到规范计算结果的安全性。杨玉泽等[7]将基于p-y曲线理论所建立的计算式与桩基水平静载试验结果进行对比,验证了计算式的有效性与准确性。试验分析法主要分为模型试验法和现场试验法。Davissin 和Salley[8]采用模型试验法,以铝合金管模拟水平荷载作用下桩土之间的相互作用。朱焰[9]对吸力式桩桶与土之间的抗拔力进行研究,采用模型试验法对其进行测量且提出了初步的计算理论,并与现场试验所测得的数据进行比对,结果基本一致。张苇等[10]通过对3种不同长径比、3种不同荷载作用角度下吸力式单桩基础进行室内模拟试验,研究了饱和砂土下吸力单桩极限抗斜拉承载力。有限元分析法是利用数学建模的方法对研究系统进行模拟,利用单元之间的相互作用,以有限量的未知单元去逼近无限量的未知单元来达到研究系统的真实性,是目前岩土工程中研究桩土相互作用的主要方法之一。Achmus和Abdel-Rahman[11]采用有限元分析法对波浪作用下桩土相互作用以及桩基础变形程度进行了研究。刘红军等[12]通过数值模拟对水平荷载下单桩基础的桩土相互作用进行研究。孙立强等[13]研究了倾斜荷载作用下吸力桶不排水上拔承载特性,得出了倾斜荷载下吸力桶承载力的计算方法。孔德森等[14]采用有限元软件ABAQUS 建立了海上风电单桩基础与土相互作用数值模型,研究表明随着循环荷载比的增加,桩身位移零点和桩身剪力反弯点沿埋深逐渐下移。赵密等[15]采用有限元分析法,建立了一种三维桩土相互作用模型,研究了在同一水体中不同桩体、土体参数下桩体位移变化。
根据以前学者的研究内容可以发现,当前国外学者对于吸力式桩的研究基本处于其外形以及桩土之间的抗拔力作用,而国内学者对于吸力式桩的研究限于桩土相互作用或者单向荷载受力情况下的承载特性问题,少有人在桩土相互作用问题的基础上对联合荷载下吸力式桩桶的承载问题进行研究。因此在以前学者研究的基础上采用有限元数值模拟软件ABAQUS,对主要承受竖向和水平联合荷载下的吸力式桩桶进行三维数值模拟,以此来探讨吸力式桩桶与海底土在受到不同的竖向和水平荷载情况下的变形程度以及承载特性问题,并引出相对应的破坏包络曲线,研究结果可为后续吸力式桩桶的设计提供参考。
1 模型分析与验证
1.1 工程原型资料
文中计算的工程原型采用Bransby 和Randolph[16]提到的澳大利亚西北大陆架砂土环境下某裙式基础(桶形基础),该基础的大致形状如图1所示,该土体模型采用Tresca材料模型。
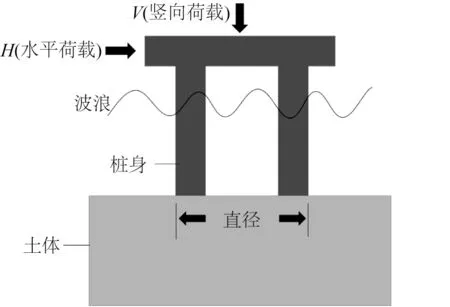
图1 近海裙式基础Fig.1 Offshore skirt foundation
由于Bransby和Randolph[16]所采用的Tresca材料模型与静水压无关,若单纯继续延用在文中土体模型中将会在实际工程引起不可忽视的偏差,因此在该模型的基础上,将土体模型改用较为理想的摩尔库伦屈服准则,并采用ABAQUS 有限元分析软件,对砂土环境下吸力式桩桶受到大小不同的V-H 联合荷载时桩土承载特性和受到0°、15°、30°、45°、60°、75°和90°的倾斜荷载时桩体相应的破坏包络曲线进行研究。
1.2 有限元模型
有限元模型是将研究对象的结构分割成单元网格的形式来模拟实际情况下的结构状况。模型主要以中国东海砂土环境为研究背景建立吸力式桩桶的有限元模型,建模过程主要包括以下5个步骤:材料参数选取、分析步设置、桩土相互作用设置、网格划分以及模型验证结果分析,其中前4个步骤的分析参数根据反复大量的数值模拟数据以及以往学者的经验进行敲定。
1.2.1 模型构建和材料参数
桩体部分采用钢质桩,并考虑到桩桶桶壁厚度;土体选择长方形土体;模型整体采用剖面半结构形式,便于模型的简化,从而提高模型的计算效率。模型具体材料参数详见表1和表2。

表1 桩体模型尺寸及材料参数Tab.1 Pile model size and material parameter

表2 土体模型尺寸及材料参数Tab.2 Soil model size and material parameter
1.2.2 分析步设置
设置的模型加载状态处于静力通用条件下,并调整增量步以保证模型在后续计算中的收敛性,方程求解矩阵选择非对称形式。
模型中以直角坐标系中的y轴为重力及竖向荷载加载方向,负向为正;以x轴为水平荷载加载方向,正向为正。在实际施工环境中,可以认定土体位移为0,但内部存在初始地应力,若不将地应力进行平衡,则模型的位移变化将会较大,与实际工程状态不符,因此在后续加载前需要将地应力进行平衡处理。在地应力处理方面,将土体前一轮计算的应力值导入模型作为下一轮计算的初始应力,反复进行模型初始应力的平衡并已使土体位移达到10-6m以下,之后再进行后续的加载计算。
1.2.3 桩土相互作用设置
由于在施工中桩土是分开的,因此需要对桩土之间相互作用的接触形式进行定义。在建模过程中,分别构建模型桩体和土体表面,并建立桩—土相应的接触形式。模型采用主—从接触面算法进行分析,其能使模型表面网格划分更加精细,若网格的密度比较接近,则应该选择较为刚性的材料作为主面,较为柔性的材料作为从面,因此模型选择桩体为主面,土体为从面。桩底与土体接触部分进行绑定处理,其余面接触形式定义为摩擦接触,切向行为中摩擦系数为0.3,法向行为默认不变。在定义桩体侧面接触时,需要将桩桶内外壁接触面进行中心划分为4个接触面,以保证后续计算过程中不会因为弧度方向问题而导致模型不收敛。
1.2.4 网格划分
为了更加接近现实,使模型更加精细,网格单元类型采用C3D8R,网格属性采取六面体扫掠,桩体的网格全局尺寸为0.35,土体的全局尺寸为2,其中桩土接触部分需要进行局部种子定义加密处理,远离接触面的土体部分可适当放大网格密度。边界条件为四周法向固定,底面为完全固定。图2 为划分网格后的吸力式桩桶有限元模型。

图2 吸力式桩桶网格划分Fig.2 Grid division of suction pile barrel
1.2.5 模型验证
1)p-y曲线法
p-y曲线是描述泥面下某一深度截面上模型土抗力与桩身挠度之间的关系曲线,其可以较好地反映出桩土之间相互作用的变形特性,是一种考虑土体非线性关系的复合分析法[17-18]。对于砂土地基,目前采用API规范[19]中计算方法导出的p-y曲线,计算形式如下:
式中:p为泥面下z深度处的地基土抗力,Pa;Ψ为计算系数,也称修正系数;pu为极限土抗力,Pa;k为地基反力初始模量;z为泥面以下的深度,m;y为水平位移,m;d为桩径,m;C1、C2、C3为与内摩擦角相关系数。
式(1)中初始模量k和式(3)中内摩擦角相关系数C1、C2、C3的取值大小参考API 规范[19],详见表3和表4。
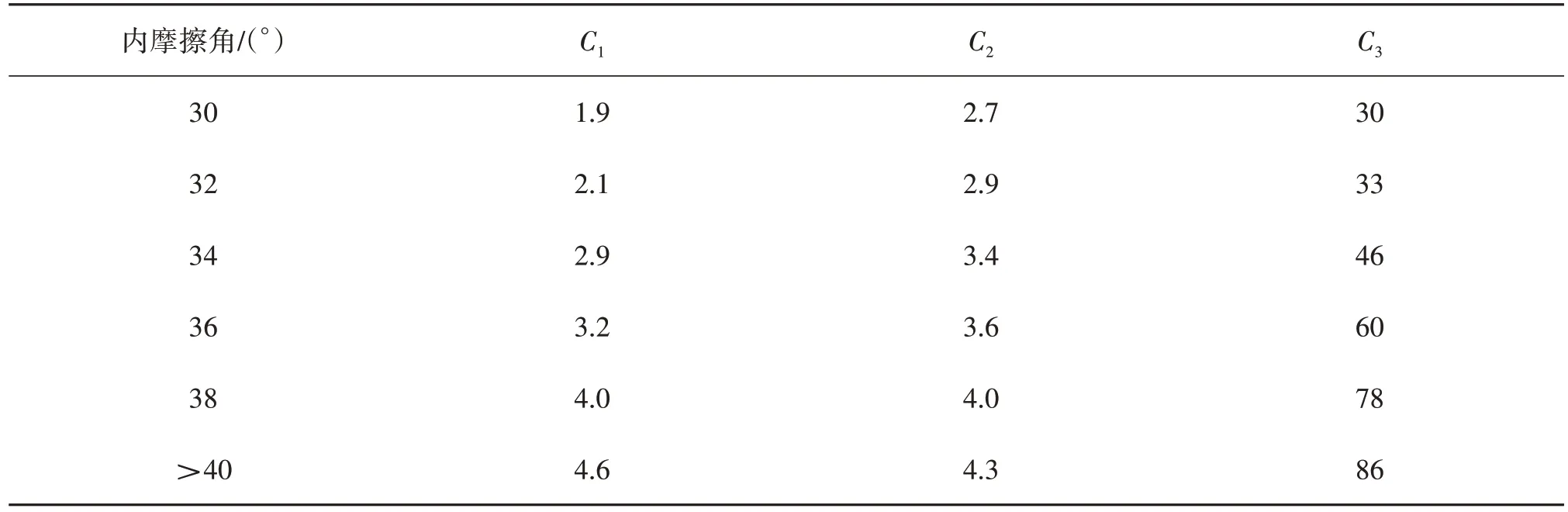
表3 系数C1、C2、C3函数值Tab.3 Coefficients C1, C2 ,C3 function values

表4 地基反力初始模量Tab.4 Initial modulus of foundation reaction
为了进一步改善p-y曲线的适用范围,文献[20-22]基于离心状态下吸力桶模型试验的结果提出了p-y曲线的双曲模型,计算公式见式(4)。
2) 模型对比
为了验证该有限元模型的合理性,选取泥面下9 m 某一个积分结点,将文中有限元计算结果与API规范计算结果绘制的曲线进行对比,结果如图3 所示。图3 的结果表明,有限元计算结果与API规范计算结果基本一致,但有个别计算数据存在偏差,是因为API规范所考虑的情况相较于有限元模型计算一般比较理想。
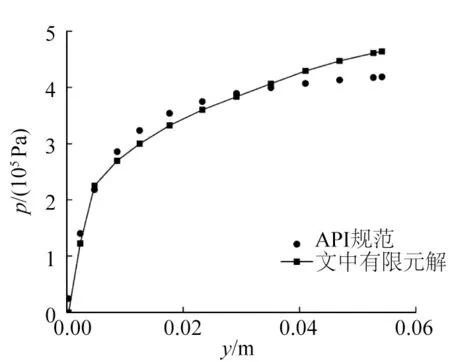
图3 有限元解与API规范的p-y曲线对比Fig.3 Comparison of p-y curve between finite element solution and API specification
2 桩土承载特性分析
2.1 桩体承载特性分析
在有限元模型分析中,根据对该模型反复大量的数值模拟计算以及以往学者的试验经验,最终对吸力式桩桶在土体外部裸露的桶盖部分同时施加大小如表5 所示的等距竖向和水平联合荷载,然后分析在不同荷载情况下模型桩顶的应力变化以及桩身弯矩变化情况。
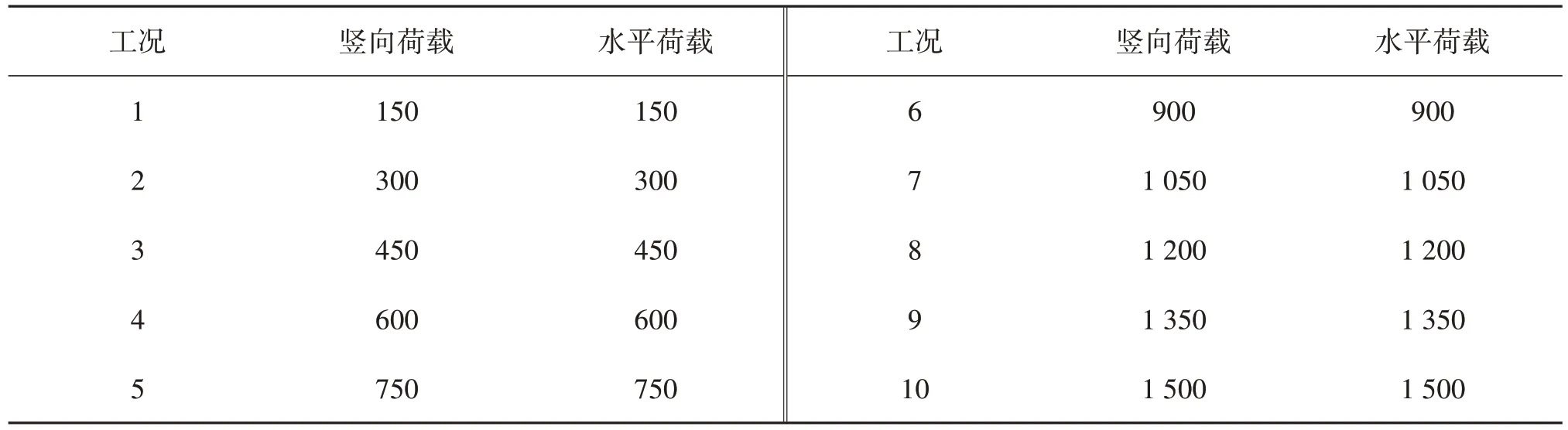
表5 模型施加竖向与水平荷载Tab.5 Vertical and horizontal loads applied to the model 单位:kN
当桩体受到荷载作用时,其变形主要为竖直和水平方向的挠曲变形,在ABAQUS 有限元分析软件可视化处理后,可以根据帧率选择来对应到不同分析时间所显示的位移分布云图。图4为桩体在150 kN 荷载作用下有限元计算过程中不同分析步时间对应的位移云图,可以看出随着计算时间的变化,桩身最大位移变化逐渐向施加荷载处偏移。
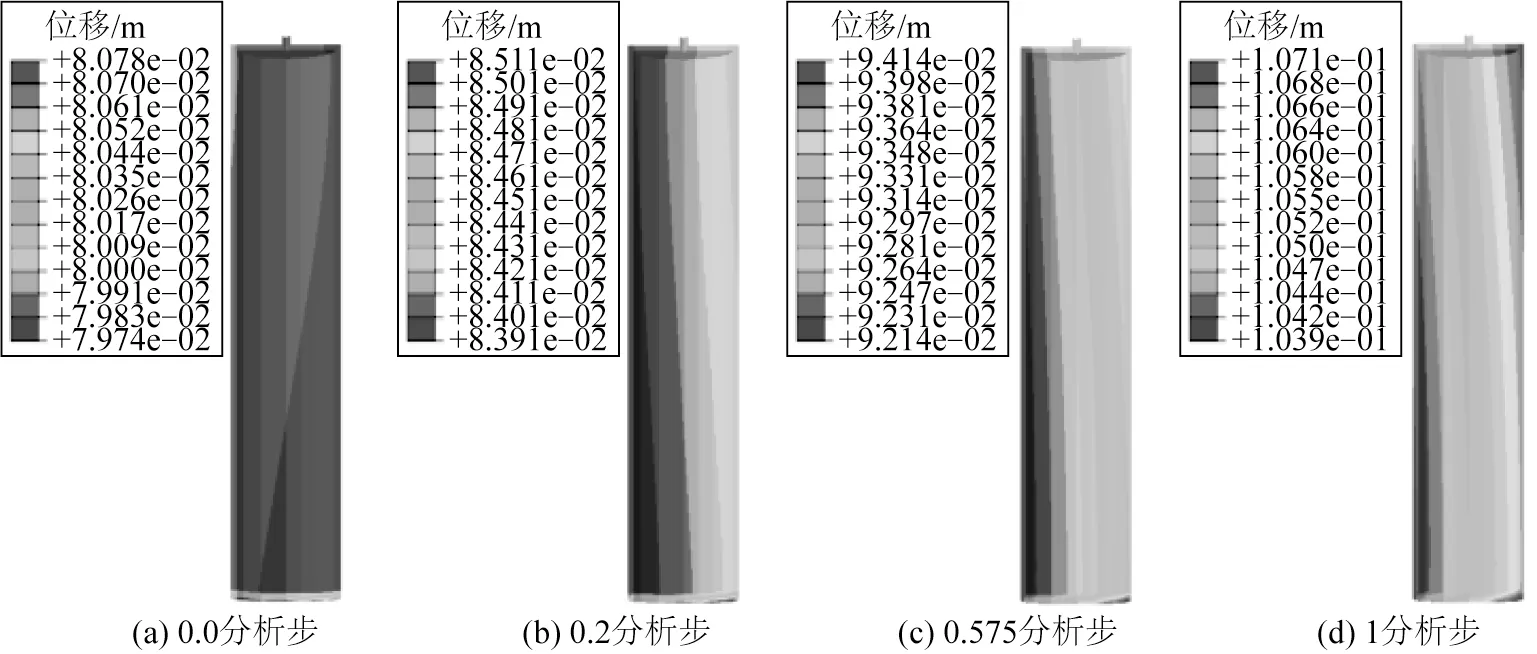
图4 桩身整体位移云图Fig.4 The whole displacement cloud of the pile body
图5为不同荷载下不同分析步时间桩身位移最大处对应的应力变化曲线。根据不同荷载下的桩顶应力变化曲线可以看出随着荷载的加大,计算迭代过程中的应力变化趋势基本一致,呈递增状态。当150 kN 荷载下桩顶位移达到极限值时,桩体最大应力为3.31 MPa。

图5 桩顶应力变化曲线Fig.5 Stress change curve of pile top
图6 为施加不同荷载后的桩身弯矩。在静力状态下对桩顶施加不同大小的V-H 联合荷载时,桩体在竖直和水平方向均有相对应的挠曲变形。
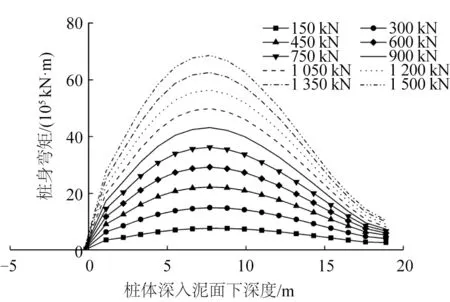
图6 不同荷载下桩身弯矩变化曲线Fig.6 Bending moment variation curve of pile shaft under different loads
由图6可以看出,对于某一特定的V-H联合荷载而言,桩体本身的挠曲变形会随着泥面下深度的增加而变大,当泥面下深度增加到一定程度后弯矩开始减小,并且施加在桩体上的V-H 联合荷载越大,桩身弯矩的最大值越大,其最大值大约位于泥面下7.7 m左右深度处。
2.2 土体承载特性分析
图7 为桩体受到150 kN 的V-H 联合荷载后土体的应力分布云图,可以根据应力分布云图看出当土体受到由桩传递的某一特定荷载时,应力变化集中在与桩体接触的地方,但随着与接触面距离的拉远,应力变化的趋势也在减小,呈均匀分布状态,这是因为土体靠近桩体的部分由于受到桩体的挤压而产生土抗力,距离桩体越远,土体受到挤压作用便越小,其土抗力也会随之减小,其应力变化程度也逐渐趋于均匀。
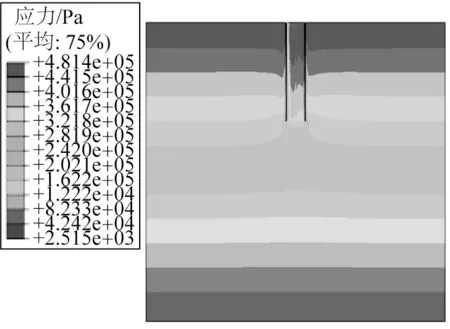
图7 受载后土体的应力云图Fig.7 Stress nephogram of soil mass after loading
图8 为施加150 kN 荷载后土体的位移云图。由图8 可以看出,土体发生最大位移的区域在桩体受到荷载作用表面的附近,由于吸力式桩桶与钢管桩不同,其桶体内部也存在土体,并且内部土体是主要受到桩体荷载传递的对象,因此土体的整体变形主要发生在桩桶内部以及桩桶桶壁附近,位移最大值处于桩体受载表面附近的土体,随着与桩体接触表面距离的拉远,其土体变形程度也在减小。图9为150 kN的V-H荷载作用下土体的塑性应变,可以看出土体发生塑性应变的主要区域集中在与桩桶内壁接触的土体部分,而远离桩土接触面的部分,塑性应变程度较小可忽略不计。
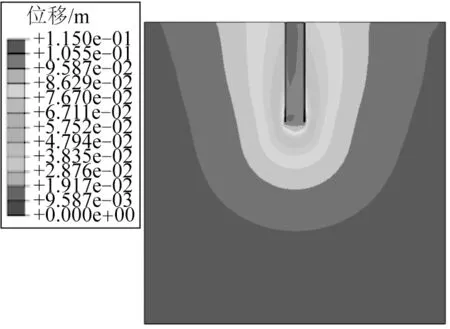
图8 受载后土体的位移云图Fig.8 Displacement change curve of soil mass after loading
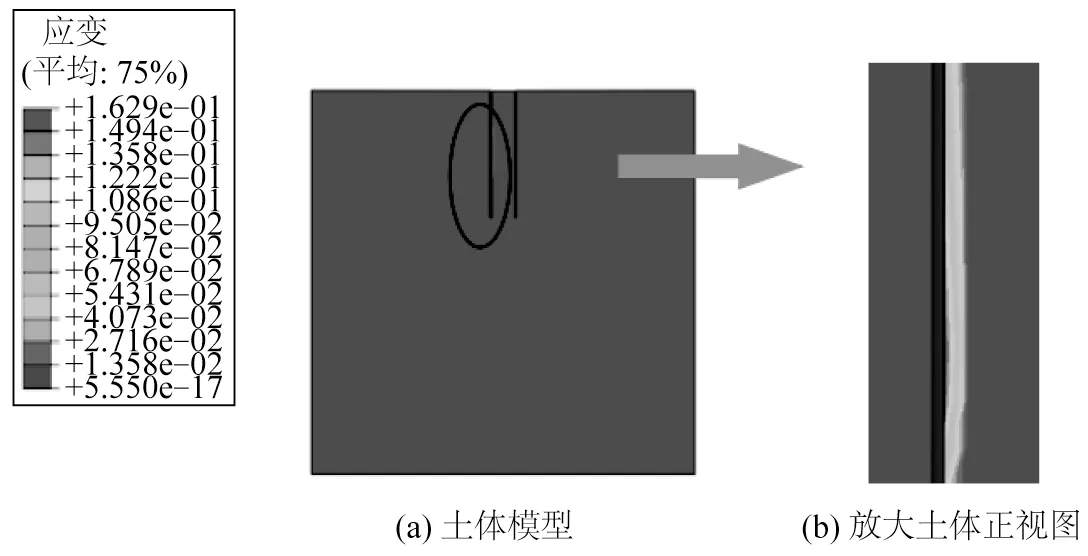
图9 受载后土体塑性应变Fig.9 Plastic strain diagram of soil after loading
3 破坏包络面特性分析
3.1 模型加载方式
对于V-H 联合荷载作用面,可以将竖向和水平荷载合为有倾斜角度的表面荷载,并采用分级作用力的加载方式[23]。将倾斜角度分为0°、15°、30°、45°、60°、75°、90°这7 组进行试验计算,在试验的过程中,对模型的位移—荷载曲线进行监控,并由计算结果导出桩体模型的RF 值,即模型加载过程中桩土相互作用所体现的反作用力,其中最大值作为桩体的极限承载力,并根据极限承载力的大小绘制出对应的包络曲线。
3.2 V⁃H加载面上的包络曲线
表6为吸力式桩桶在受到倾斜程度不同的表面荷载时所得到的极限承载力以及竖向和水平的承载力分量。根据表6 可以得到V-H 荷载作用下桩体的屈服点。图10 为根据屈服点所绘制的包络线。为了验证通过有限元解所绘制的包络曲线的正确性,选取文献[16]和文献[24]中模拟结果与文中的结果进行对比。从图10 可以看出文中的加载方式绘制的包络曲线与Bransby 和Randolph[16]所研究的V-H-M 荷载下裙式基础(桶形基础)破坏包络曲线以及范庆来和栾茂田[24]对桶形基础破坏包络面研究中3种加载方式所绘制的包络曲线趋势基本一致,但由于加载方式的不同,个别极限荷载组合点存在细微的误差。
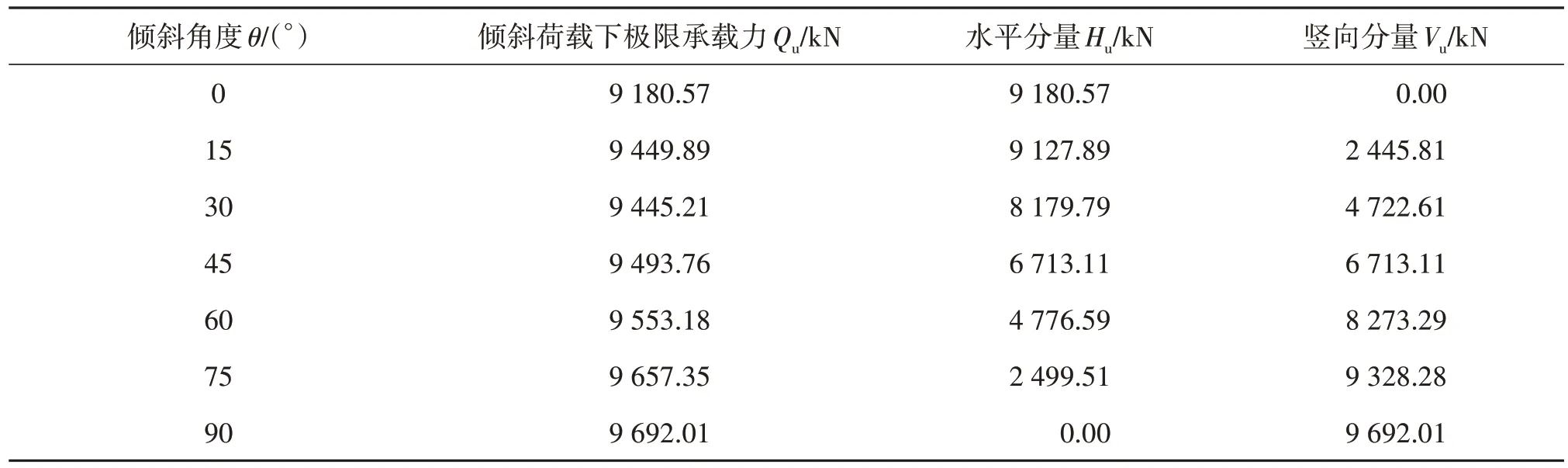
表6 V⁃H荷载下桩体极限承载力Tab.6 Ultimate bearing capacity of pile under V⁃H load
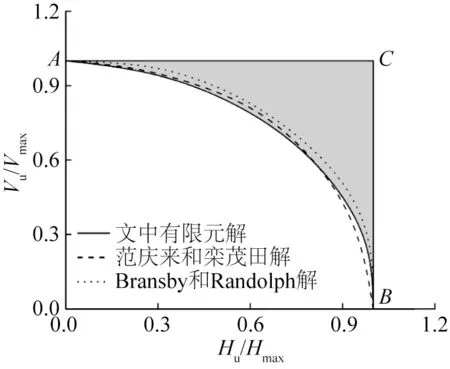
图10 V-H荷载下的包络曲线Fig.10 Envelope curve under V-H load
范庆来和栾茂田[24]、Bransby和Randolph[16]所采用的swipe加载方法是通过对加载路径进行分析,从而找出路径上的各个极限荷载组合点而得出最终的破坏包络曲线,优点在于分析位移荷载路径后包络曲线上的各个组合荷载可以直接得出。而文中的加载形式为表面荷载,与swipe 加载方式不同于需要对模型计算结果进行处理,不用对位移荷载路径进行分析,由ABAQUS 求出整体模型的RF值,从而导出其破坏包络曲线,但两种加载方式最终都需要对极限承载力进行分析。图10中A、B两点所在垂直于y轴和x轴的直线相交于C点,阴影部分在实际中属于破坏区域,也是按照实际工程中计算结果所存在的安全隐患,因此要避免极限承载力出现在阴影部分从而避免安全事故的发生。
在得出包络曲线之后,根据origin2022软件对该包络线进行数据拟合,可以得出其表达式:
式中:Vmax代表最大竖向承载力,大小为9 692.01 kN;Hmax代表最大水平承载力,大小为9 180.57 kN;α代表倾斜荷载与水平面的夹角,可以通过式(6)来对Vu、Hu以及α进行相互求解。
4 结 语
运用ABAQUS 有限元分析软件,绘制出了吸力式桩桶模型的p-y曲线,并与API 规范中的计算方法进行比较,结果基本一致,验证了文中有限元模型的可行性。针对不同表面荷载下桩体和土体的承载特性进行探讨,得到以下结论:
1)桩体在受到荷载作用过程中的桩顶位移呈递增状态,桩身的最大应力出现在桩顶受载部分,最大弯矩由于力的传递性则出现在泥面下7.7 m左右处。
2)土体的位移和应力均由桩体受到荷载作用后,土体受到挤压作用而导致。对于土体的应力状态而言,主要存在于桩土相互作用的表面处;对于土体的变形而言,主要存在于桩体内部以及与桩表面相互作用的土体,且变形大小以桩顶向桩底以及四周呈递减趋势传递;土的塑性应变主要分布在桩土接触面附近,随着远离接触面,土体的塑性应变可忽略不计。
3)桩体在受到倾斜角度不同的表面荷载时所绘制的破坏包络曲线大致为四分之一的椭圆形状,且倾斜角度不同,桩体所能体现的极限承载力也大不相同。根据ABAQUS 有限元软件所绘制的包络图能体现出桩体的破坏区域,在实际工程中应当避免该现象的发生。

